风积砂-黄土过渡型砂性黄土动力特性试验研究*
骆建文 李喜安 赵 宁 周 健 赵兴考
LUO Jianwen① LI Xi’an②③ ZHAO Ning② ZHOU Jian④ ZHAO Xingkao⑤
风积砂-黄土过渡型砂性黄土动力特性试验研究*
骆建文①李喜安②③赵 宁②周 健④赵兴考⑤

随着沙漠-黄土高原过渡地带各类资源的不断勘探和开发,对风积砂-黄土过渡型砂性黄土的动力特性缺乏了解这一问题愈来愈成为此类地区地震与人工动力相关工程建设发展的制约因素。本文在等压固结条件下,通过进行室内固结不排水动三轴试验,获得了风积砂-黄土过渡型砂性黄土的动力学参数,并以此为基础绘制了风积砂-黄土过渡型砂性黄土的动应力-应变关系曲线,探讨了风积砂-黄土过渡型砂性黄土动模量的变化特征、阻尼比随动剪应变变化的曲线关系及适合的拟合模型,进一步建立了适用于风积砂-黄土过渡型砂性黄土的等效动黏弹性本构模型。结果表明:Hardin双曲线模型对风积砂-黄土过渡型砂性黄土动剪切模量与动剪应变关系曲线的拟合较好,而幂函数经验公式对阻尼比与动剪应变关系曲线的拟合较好。本文研究结果为风积砂-黄土过渡型砂性黄土动力特性的研究提供了基础。
砂性黄土 动三轴试验 动应力 动应变 动模量
LUO Jianwen①LI Xi’an②③ZHAO Ning②ZHOU Jian④ZHAO Xingkao⑤

0 引 言
随着西部大开发战略的深入实施,中西部地区的资源勘探、经济建设等工程建设活动愈加增多,由于沙漠-黄土高原过渡地带的不断开发,在该地区有关动力荷载的各类工程问题逐渐显现,建设人员在风积砂-黄土过渡型砂性黄土分布区的工程实践中也遇到了越来越多与动力荷载相关的技术难题。
土在动力荷载作用下表现为具有弹性、塑性和黏滞性的黏弹塑性体,加之本身具备明显的各向异性,使土的动应力-应变关系变得极为复杂(吴世明, 2000)。正因如此,伴随着土动力学的发展和黄土地区建筑物抗震稳定性分析的要求,黄土动力学的研究已经展开并取得了许多初步成果(宋章等, 2009)。诸如谢定义(1988, 1999)通过对黄土施加等幅正弦循环荷载,研究黄土的动应力-应变关系、动强度、动弹性模量和阻尼比等动力学参数。张振中等则对随机地震荷载作用下的黄土施加随机地震波,以此对不同地震荷载作用下黄土的动本构模型、动强度、动弹性模量和阻尼比展开了大量的对比研究工作,获得了较好的试验结果(王峻等, 1992; 张振中, 1999)。王峻、王兰民等对不规则地震波和等效正弦波进行了比较,发现了黄土在随机地震荷载和等幅正弦荷载作用下的震陷量预测结果存在一定的差别(王峻等, 1997, 2011; 卞敬玲等, 2001)。另外,在建立黄土动本构模型方面,Hardin和Dmevich提出的双曲模型以及相关改进模型已得到相对广泛的应用(邓龙胜等, 2012)。
综上所述,虽然当前对于黄土动力学的研究已有了一批成果,但截至目前,研究对象多是集中在砂土或黏性黄土,对风积砂-黄土过渡型砂性黄土的动力特性却很少有人涉及,对其相应地层工程地质性质方面的理论研究更是十分缺乏,这一现状已经成为当地地震与人工动力相关工程建设发展的关键制约因素。故而,研究循环荷载下的风积砂-黄土过渡型砂性黄土的动力特性对沙漠-黄土高原过渡地带的各种动力地基及地震成因黄土滑坡的治理、设计以及施工实践都具有极为重要的理论和工程实际意义。
本文为获取循环荷载作用下沙漠-黄土高原过渡地带风积砂-黄土过渡型砂性黄土的动力特性曲线及动力学参数,以室内固结不排水动三轴试验为主要技术手段,分析并探讨了动模量的变化特征、阻尼比随动剪应变变化的曲线关系及合适、有效的拟合模型,在此基础上进一步建立风积砂-黄土过渡型砂性黄土的等效动黏弹性本构模型。其结果为风积砂-黄土过渡型砂性黄土动力特性的研究提供了基础,并对沙漠-黄土高原过渡地带实际工程的设计施工具有一定的参考价值。
1 理论模型介绍
1.1 双曲线模型
由Konder(1963)和Hardin et al.(1972)等人提出用来描述土的动应力-应变关系曲线的双曲线是最常见的曲线模型,即:
(1)
式中,τ为动应力;γ为应变;a、b为土的试验参数。
根据双曲线表达式可以得到卸载、再加载曲线方程,即:
(2)
(3)
其中式(2)为卸荷方程、式(3)为再加载方程,式中,Gmax为循环荷载作用下土的初始(最大)模量;τa为应力幅值;γa为应变幅值;γr为参考应变。
在土动力学中,阻尼比λ的表述为实际的阻尼系数c与临界阻尼系数ccr之比。对数减幅系数δ及能量损失数ψ与阻尼比λ之间的关系为(谢定义,1988):
(4)
由上述阻尼比理论及双曲线模型整理可以得到动模量和阻尼比与应变关系的曲线方程分别为:
(5)
(6)
双曲模型虽然简单,但对拟合阻尼比λ效果很不理想。为此,在工程上对于拟合阻尼比使用较多的是幂函数经验公式和陈国兴经验公式,分别如下所示:
幂函数经验公式为:
(7)
式中,λ0为土的最大阻尼比;β为阻尼比曲线的形状系数,与土的性质有关的拟合参数。
陈国兴(2007)经验公式为:
(8)
式中,λmin为土的基本阻尼比; λ0、β为阻尼比曲线的形状系数,与土的性质有关的拟合参数。
本文将对上述两种拟合方式进行比较,以确定更适合沙漠-黄土高原过渡地带风积砂-黄土过渡型砂性黄土的拟合方法。
1.2 等效动黏弹性模型
土的等效动黏弹性模型是将土视为黏弹性体,这也是常见的土动应力-应变本构关系模型(慕焕东等, 2014),该本构模型选用剪切模量和阻尼比来体现土的动应力-应变关系的非线性与滞后性,这种简单、清晰的表达方式具有概念明确、应用方便的优点(陈国兴, 2007; 邓亚虹等, 2012; 慕焕东, 2014)。
2 试验方案
本次试验所用仪器是国土资源部岩土工程开放研究实验室的W3Z20型动三轴试验系统。土样来源为沙漠-黄土高原过渡地带深度3m的风积砂-黄土过渡型砂性黄土,并以1.65g·cm-3干密度的重塑试样进行试验。土样的颗粒大小分布累积曲线(图1),试验试样的基本物理参数(表1)。按照《土工试验规程》(SL237-1999)将试验土柱制成φ39.1mm×80mm的圆柱形试样。采用CU法对饱和试样进行动三轴试验,将真空饱和过的试样在50kPa、100kPa、150kPa和200kPa的条件下等压固结,并输入频率为1Hz的正弦波。

图1 土样的颗粒大小分布累积曲线
表1 试样的基本物理参数
Table1 Basic physical parameters of the sample

取样深度/m天然密度ρ/g·cm-3天然含水率W/%塑限WP/%液限WL/%31.6510.915.1427.67
3 试验结果及分析
3.1 动模量
图2为根据试验绘制的干密度为1.65g·cm-3的风积砂-黄土过渡型砂性黄土试样在50kPa、100kPa、150kPa和200kPa围压下的动应力-应变关系曲线(τd-γd)。风积砂-黄土过渡型砂性黄土动应力-应变关系曲线随着动剪应变幅值的增大,其斜率有逐渐变缓的趋势,且在较大动应变时变化幅度明显,曲线变化趋势基本符合Hardin双曲线模型。
若动应力-应变关系曲线基本满足Hardin双曲线模型,则动模量倒数-动应变关系(1/Gd-γd)拟合结果应呈线性关系(慕焕东, 2014)。通过图2 可以获得相关参数,并由此可得到动模量倒数与动剪应变关系及其拟合曲线,以验证模型适用性,绘制曲线(图3)。比较不同围压下的拟合结果,可以发现试验数据点除在大剪应变时有较小误差,整体趋势与拟合曲线吻合较好,所有拟合相关系数均在0.99以上。由此可以得出Hardin双曲线模型对风积砂-黄土过渡型砂性黄土的动应力-应变曲线具有适用性。根据拟合结果可以得到该拟合曲线在纵轴上的截距,其倒数值代表风积砂-黄土过渡型砂性黄土在不同围压下的初始(最大)模量(宋焱勋, 2011),回归参数(表2)。从表2可以看出,风积砂-黄土过渡型砂性黄土试样的初始(最大)模量随着固结围压的增大而线性增加。
表2 线性拟合回归参数
Table2 Linear fitting regression parameters

回归方程固结围压Kc/kPa回归参数abGmax/MPa1/Gd=a+b*γd500.024615.933140.651000.022813.768743.861500.019912.059550.252000.01609.627562.50

图2 τd-γd关系曲线

图3 1/Gd-γd关系曲线

图4 Gd/Gmax-γd关系曲线及λ-γd关系曲线
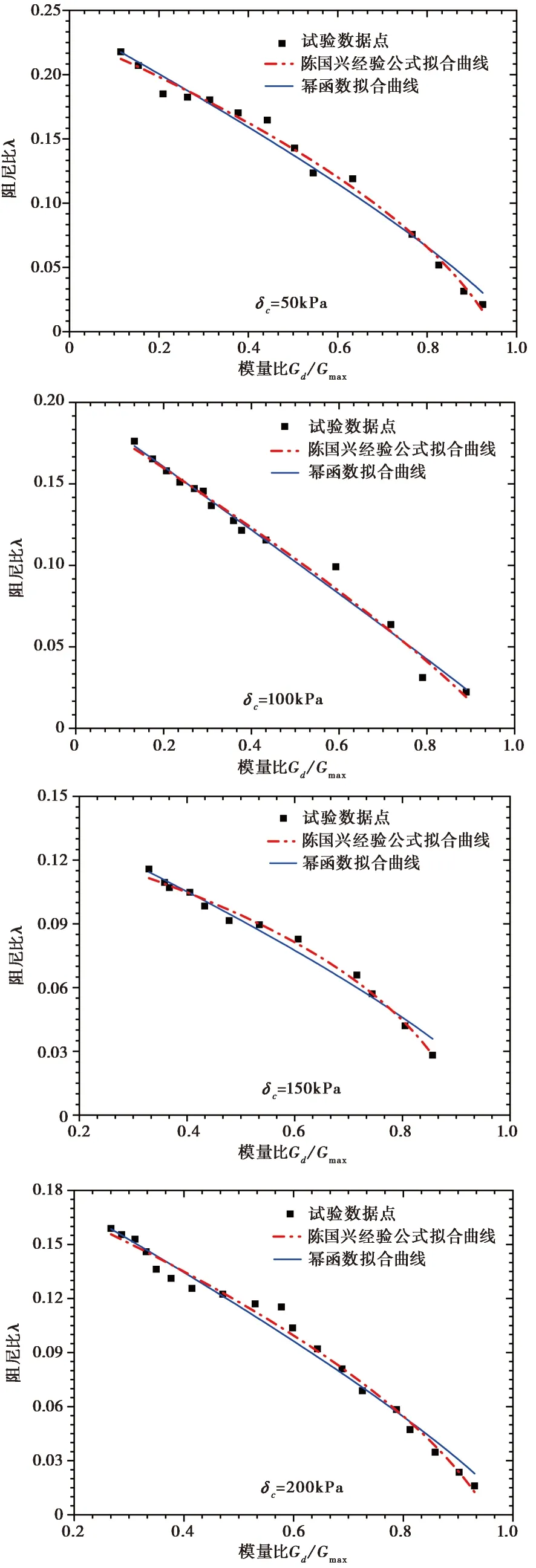
图5 不同模型拟合曲线比较
3.2 阻尼比
由实际试验数据可以得到动模量比、阻尼比与动剪应变的试验曲线(Gd/Gamx-γd,λ-γd),又进一步根据前述式(5)、式(6)可以得到动模量比、阻尼比与动剪应变的双曲模型拟合曲线,并最终绘制曲线(图4)。由图可知,动模量比试验曲线整体变化趋势与双曲模型拟合曲线变化趋势吻合度较高,此规律再次验证了图3 所得结论。而阻尼比试验曲线整体变化趋势与双曲模型拟合曲线变化趋势吻合度较低,仅在小剪应变时出现数值相近情况,随着动应变幅值的增加,实验数据会逐渐趋于稳定状态,阻尼比双曲模型理论数值开始明显高于试验数据,这是由于模型本身的不适宜性造成的误差逐渐增大,拟合效果不理想。
在实际应用中常见的拟合阻尼比的函数模型是幂函数经验公式和陈国兴经验公式,拟合结果(图5)。幂函数经验公式曲线回归参数最大阻尼比λmax和曲线形状系数β(表3),陈国兴经验公式曲线回归参数基本阻尼比λmin和曲线形状系数λ0、β(表4)。从图5 所示拟合结果并结合表3、表4列出的相关系数可以看出,在阻尼比拟合方面,幂函数经验公式与陈国兴经验公式对于趋势与数值的拟合都具有较高的精度,且相关系数均在97%以上。但根据表4显示的回归参数可以发现,在不同围压下,陈国兴经验公示模型的基本阻尼比均出现了负值的情况,这不符合阻尼比的物理意义,故采用幂函数经验公式拟合风积砂-黄土过渡型砂性黄土的阻尼比效果更好。从表3可以得到,幂函数经验公式曲线回归参数与固结围压并没有直接关联且变化幅度较小,最大阻尼比λmax和曲线形状系数β平均值分别为0.1994和0.8342。
表3 幂函数经验公式回归曲线参数
Table3 Parameters of power function empirical formula regression curve

回归模型固结围压Kc/kPa回归参数R2λmaxβy=λmax(1-x)β500.23980.80240.9821000.19880.95960.9831500.1540.7520.9782000.20480.82290.982均值0.19940.83420.981
表4 陈国兴经验公式回归曲线参数
Table4 Parameters of Chen Guoxing empirical formula regression curve

回归模型固结围压Kc/kPa回归参数R2λminλ0βy=λmin+λ0(1-x)β50-0.05870.28900.52310.989100-0.01630.21090.80930.983150-0.27790.41440.15580.99200-0.04030.23300.55720.988均值-0.09830.28680.51130.988
阻尼比与动剪应变关系拟合曲线(图6),图中分别用虚线和实线表示双曲模型拟合曲线和幂函数经验公式拟合曲线。通过比较可以发现,对阻尼比试验数据点的拟合,幂函数经验公式相比于双曲模型无论是变化趋势还是理论数值都具有较高的精度,也进一步体现了幂函数经验公式对于拟合风积砂-黄土过渡型砂性黄土的阻尼比随动剪应变变化的曲线关系是有效且适合的。
4 建立等效黏弹性本构模型
建立合适的本构模型对于分析沙漠-黄土高原过渡地带风积砂-黄土过渡型砂性黄土的动力特性是复杂且重要的。土体的等效动黏弹性模型就是将土体视为黏弹性体,并用初始(最大)动模量Gmax和等效阻尼比λ来反映土的动应力-应变关系的非线性和滞后性,因此该本构模型可以通过构造一个参数两条曲线来表示:即初始(最大)动模量Gmax、动模量随动剪应变幅值衰减曲线G/Gmax-γd和阻尼比λ随动剪应变幅值增长曲线λ-γd(宋焱勋, 2011)。明确参数和曲线后,则可用Gmax、G/Gmax-γd、λ-γd来描述风积砂-黄土过渡型砂性黄土的动应力-应变过程。
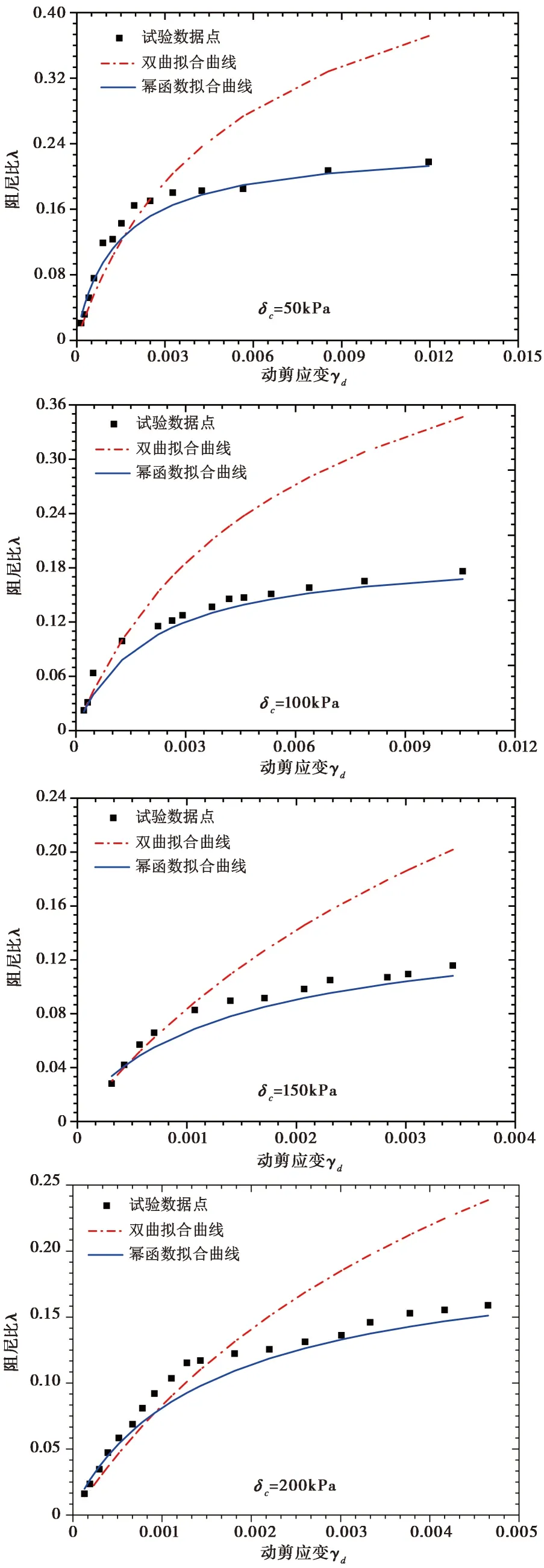
图6 阻尼比试验点曲线与双曲模型、幂函数经验公式比较
首先采用类似Seed et al.(1970)的经验公式:
(9)
在不同固结压力情况下,对由表2确定的初始(最大)动模量进行回归拟合,拟合曲线(图7),并由此可得到模型参数Kmax、n。动模量比-动应变关系曲线满足双曲模型(式6),其参考应变γr可根据表2所示线性回归参数a、b求得,计算式为a/b(邓亚虹等, 2012; 慕焕东, 2014)。阻尼比-动应变关系曲线由前文可知满足幂函数经验公式,回归参数λmax、 β如表3所示。
设定土体泊淞比νd为0.25,从而可以构建沙漠-黄土高原过渡地带风积砂-黄土过渡型砂性黄土的等效动黏弹性本构模型,模型参数(表5)。
表5 本构模型拟合参数
Table5 Fitting parameters of constitutive model

干密度/g·cm-3Kmaxnλmaxβνd1.65467.3980.32140.19940.83420.25

图7 初始模量与有效固结压力关系拟合曲线
从图7和表5可以看出,初始(最大)剪切模量Gmax与平均有效固结压力δc呈正相关关系,拟合曲线相关系数为0.7632,模型参数Kmax和n分别为467.398和0.3214。
5 结 论
本文通过对沙漠-黄土高原过渡地带风积砂-黄土过渡型砂性黄土在不同固结围压条件下,输入频率为1Hz的正弦波进行固结不排水动三轴试验,获得了动力学参数,分析了风积砂-黄土过渡型砂性黄土的动力学特性,并探讨了循环荷载作用下动模量的变化特征、阻尼比随动剪应变变化的曲线关系及适合的拟合模型,进一步建立了适用于该地区风积砂-黄土过渡型砂性黄土的等效动黏弹性本构模型。可以得到以下结论:
(1)Harding双曲线模型基本符合风积砂-黄土过渡型砂性黄土的动应力-应变曲线变化趋势,并且对动模量比与动应变关系曲线变化趋势吻合度较高。
(2)Harding双曲模型对阻尼比试验曲线仅在动应变较小时与拟合曲线吻合度较高,并随着动应变幅值的增加,阻尼比双曲模型理论数值明显高于试验数据,误差逐渐增大。
(3)通过比较发现,陈国兴经验公式不适用于沙漠-黄土高原过渡地带风积砂-黄土过渡型砂性黄土,采用幂函数经验公式拟合阻尼比变化效果更好,并且对于阻尼比与动应变关系曲线具有较高的拟合精度。
Bian J L,Luo Y S. 2001. The review and discussion on research of dynamic characteristics of loess[J]. Technique of Seepage Control,7(4): 9~15.
Chen G X. 2007. Geotechnical earthquake engineering[M]. Beijing: Science Press.
Deng L S,Fan W. 2012. Study of dynamic stress-strain relationship of loess under seimic loading[J]. Chinese Journal of Rock Mechanics and Engineering,31(S1): 3174~3180.
Deng Y H,Li L,Li X A,et al. 2012. Maowusu desert aeolian sand dynamic stress-strain test research[J]. Journal of Engineering Geology, 20(S): 64~70.
Hardin B O,Drnevich V P. 1972. Shear Modulus and curves[J]. Journal of Soil Mechanics and Foundations, ASCE,(7): 667~692.
Kondner P L. 1963. Hyperbolic stress strain response: cohesive soils[J]. Journal of Soil Mechanics and Foundations, ASCE, 89(1): 115~143.
Mu H D,Deng Y H,Peng J B. 2014. Experimental research on loess dynamic characteristics at ground fissure belt in Xi’an area[J]. Journal of Engineering Geology,22(5): 951~957.
Mu H D. 2014. Study on the seismic amplification effect on site with ground fissure[D]. Xi’an: Chang’an University.
Song Z,Cheng Q G,Zhang W. 2009. Test analysis of dynamic strength characteristics of loess soil[J]. Subgrade Engineering,(6): 65~66.
Song Y X. 2011. Test study on the mechanical property of the aeolian sand and the bearing capacity of the aeolian sand ground of Mu Us Desert[D]. Xi’an: Chang’an University.
Seed H B, Idriss I M. 1970. Soil moduli and damping factor for dynamic response analysis[R].Berkeley: Earthquake Engineering Research Center. University of California.
Wu S M. 2000. Soil dynamics[M]. Beijing: China Architecture and Building Press.
Wang J,Wang L M,Li L 1992. The effect of different seismic loadings on dynamic modulus and damping ratio of loess[J]. Journal of Natural Disasters,1(4): 75~79.
Wang J,Shi Y C,Wang J M,et al. 2011. Comparative analysis of characters of loess subsidence under different seismic loads[J]. Chinese Journal of Geotechnical Engineering,33(S1): 102~105.
Wang J,Wang L M,Li L. 1997. Laboratory prediction of seismic subsidence quantity on loess sites[J]. Northwestern Seismological Journal,19(2): 62~66.
Xie D Y. 2000. Soil dynamics[M]. Xi’an:Xi’an Jiaotong University Press.
Xie D Y. 1999. The past, present and future of the research on mechanical charateristics and application of loess[J]. Underground Space,19(4): 273~284.
Zhang Z Z. 1999. The seimic disaster forecasting of loess[M]. Beijing: Earthquake Press.
卞敬玲,骆亚生. 2001. 黄土动力特性研究回顾与探讨[J]. 防渗技术, 7(4): 9~15.
陈国兴. 2007. 岩土地震工程学[M]. 北京:科学出版社.
邓龙胜,范文. 2012. 地震荷载作用下黄土的动应力-应变关系研究[J]. 岩石力学与工程学报,31(S1): 3174~3180.
邓亚虹,李丽,李喜安,等. 2012. 毛乌素沙漠风积砂动应力-应变关系 [J]. 工程地质学报, 20(S): 64~70.
慕焕东,邓亚虹,彭建兵. 2014. 西安地区地裂缝带黄土动力特性试验研究[J]. 工程地质学报,22(5): 951~957.
慕焕东. 2014. 地裂缝场地地震放大效应研究[D]. 西安: 长安大学.
宋章,程谦恭,张炜. 2009. 黄土的动强度特性试验分析[J]. 路基工程,(6): 65~66.
宋焱勋. 2011. 毛乌素沙漠风积砂力学特性及复合地基承载力试验研究[D]. 西安: 长安大学.
吴世明. 2000. 土动力学[M]. 北京:中国建筑工业出版社.
王峻,王兰民,李兰. 1992. 不同地震荷载对黄土动模量和阻尼比的影响[J]. 自然灾害学报,1(4): 75~79.
王峻,石玉成,王杰民,等. 2011. 不同地震荷载作用下黄土震陷特性的对比分析[J]. 岩土工程学报,33(S1): 102~105.
王峻,王兰民,李兰. 1997. 黄土场地震陷量的试验预测[J]. 西北地震学报,19(2): 62~66.
谢定义. 1988. 土动力学[M]. 西安:西安交通大学出版社.
谢定义. 1999. 黄土力学特性与应用研究的过去、现在与未来[J]. 地下空间,19(4): 273~284.
张振中. 1999. 黄土地震灾害预测[M]. 北京:地震出版社.
JournalofEngineeringGeology工程地质学报 1004-9665/2016/24(5)- 0924- 07
EXPERIMENTAL STUDY ON DYNAMIC CHARACTERISTICS OF SANDY LOESS OF AEOLIAN SAND TO LOESS TRANSITIONAL ORIGIN
With the exploration and development of various kinds of resources in area of desert-loess plateau, poor understanding about the dynamic characteristics of sandy loess of aeolian sand to loess transifional origin has become the constraint more than ever in this region. This issue is particular for development of earthquakes and artificial power engineering construction. In this paper, under isotropic consolidation condition, consolidated undrained dynamic triaxial tests under different confining pressures are tested for the aeolian sand-loess transitional sandy loess. Kinetic parameters are obtained. Based on them, the dynamic stress-strain relationship of aeolian sand-loess transitional sandy loess was drawn. The change characteristic of dynamic shear modulus and damping ratio with dynamic strain of their relation curve and fitting model is explored. Equivalent dynamic visco-elastic constitutive model is further established for applicable to aeolian sand-loess transitional sandy loess. Results show that the relation curve between dynamic shear modulus and dynamic strain fits well for aeolian sand-loess transitional type of sandy loess, according to the Harding hyperbolic model. Besides, the power function model is good for fitting the relationship between damping ratio and dynamic strain. The results achieved in this paper provide basic data for the future research of dynamic characteristics of aeolian sand-loess transitional sandy loess.
Sandy loess, Dynamic triaxial tests, Dynamic stress, Dynamic strain, Dynamic modulus
10.13544/j.cnki.jeg.2016.05.022
2016-04-10;
2016-07-26.
国家自然科学基金项目(No.41172255, 41572264, 41440044),中央高校基本科研业务费项目(2014G2260008),西安长庆科技工程有限责任公司项目(CTEC(2014)Z-KY-013)资助.
骆建文(1979-),男,学士,高级工程师,从事工程地质及岩土工程勘察工作. Email: 420394101@qq.com
简介: 李喜安(1968-),男,博士,教授,博士生导师,主要从事黄土地质灾害方面的教学与科研工作. Email: dclixa@chd.edu.cn
P642.13+1
A

