钢筋混凝土框架结构动力倒塌分析方法研究∗
袁 波,王 旭,陈 耀
(贵州大学空间结构研究中心,贵州贵阳550003)
钢筋混凝土框架结构动力倒塌分析方法研究∗
袁 波∗,王 旭,陈 耀
(贵州大学空间结构研究中心,贵州贵阳550003)
本文采用了“位移法”和“反力法”对失柱的混凝土框架结构进行线性与非线性动力倒塌分析,并把位移法与反力法的分析结果进行对比,两者吻合较好,同时采用线性动力与非线性动力计算方法分别对具有相同平面布置不同高度的框架结构进行连续倒塌模拟分析,得到不同失效时间失效点的位移时程曲线。分析结果表明:柱的失效时间对位移法和反力法线性动力分析结果影响较小,随着失效时间的增大,结构的动力效应趋于收敛;柱的失效时间对位移法和反力法非线性动力分析结果影响较大,但是随着失效时间的增加,结构的动力效应趋于收敛。
位移法;反力法;混凝土框架;连续性倒塌;失效时间
结构的连续性倒塌,是指结构在非常规荷载作用下发生局部破坏,结构发生内力重分布引起其它部分破坏,进而形成连锁反应,导致结构部分或全部倒塌。连续倒塌往往会导致惨重的人员伤亡和财产损失,进行连续倒塌分析以研究结构的倒塌机理以及抗倒塌设计方法愈来愈引起人们的重视。自六十年代以来,连续倒塌的研究经历了三个高峰期,每个高峰期都是由标志性的倒塌事件引起[1-5]:1968年,英国伦敦Ronan Point公寓因煤气泄漏而发生爆炸,导致局部墙板破坏以及连续性倒塌破坏,从而掀起了连续性倒塌研究第一次高潮。1995年美国俄克拉荷马州 Alfred P.Murrah政府大楼遭汽车炸弹袭击后发生倒塌。2001年9月11日纽约世贸大楼整体性倒塌事件使连续性倒塌研究达到了另一个高潮。2004年法国戴高乐机场顶棚倒塌、2005年德国巴特莱哈尔溜冰馆、波兰卡托维茨国际博览会展厅倒塌、2006年初莫斯科鲍曼市场屋顶坍塌等事故突显了突发事件下大型公共建筑物连续性倒塌研究具有重要性和紧迫性。导致结构倒塌的偶然事故,无论源于自然因素,还是人为因素(包括非主观故意和有意为之的破坏),都不仅破坏力巨大,而且难以预见、难以控制,使得这类事故难以纳入已有的基于概率统计的荷载(作用)分析方法中。由这样性质的事故作用引发的局部破坏,也同样难以预测。因此关于结构体系连续性倒塌的研究,不仅具有紧迫的社会需求,也为研究者提出了许多难题。
1 连续倒塌分析方法
结构连续倒塌分析方法与常用的结构分析方法类似,主要有线弹性静力分析、线弹性动力分析、非线性静力分析、非线性动力分析[4-8]。线弹性静力分析:首先确定失效构件的位置,然后移除该处的竖向支撑构件,并对整体结构施加重力荷载(失效支撑构件受力范围内施加两倍的荷载,以考虑动力效应),最后对结构进行线弹性静力分析。这种方法的优点是相对简单,容易实现,但没有考虑材料非线性和动力特性。线弹性动力分析:对结构整体施加重力荷载,然后移去失效支撑杆件,在重力荷载作用下结构失去稳定产生线弹性运动。这种方法通常比静力方法要精确,可更合理的考虑连续倒塌过程的惯性力和阻尼力等动力特性。但此方法没有考虑材料的非线性,分析也比较复杂,对于产生较大塑性变形的结构来说分析结果有较大误差。非线性静力分析:此方法与线性静力分析相同,只是在分析过程中考虑了材料的非线性影响。非线性时程分析:分析过程与线性动力分析相同,此法在分析过程中考虑了材料的非线性影响,更能反映支撑构件失效时结构的动态响应,这种方法同时考虑了动力特性和材料非线性,能够提供更为理想的结果,但分析过程可能比较耗时,操作较为复杂。
2 连续倒塌动力分析
2.1 反力方法
采用瞬时加载法对框架进行连续倒塌分析。分两步实施[9-11]:(1)去掉失效构件,并将其端部内力向量P0反向作用在剩余结构上,得到的分析模型与原结构静力等效。(2)在上一步分析的基础上,在失效点(即失效构件的端点)作用如图1所示随时间变化的荷载向量p进行动力分析。图中,tf表示构件失效时间。

图1 荷载-时间曲线(反力法)
对底层中柱失效后的剩余结构进行模态分析,可得基本周期T及前二阶频率ω1、ω2,前者用来确定构件失效时间,后者用以确定瑞雷阻尼的比例系数,瑞雷阻尼可以表示为
C=αM+βK
式中:C、M及K分别为阻尼矩阵、质量矩阵及刚度矩阵;α、β分别为质量阻尼系数和刚度阻尼系数。

式中:ξ1、ξ2分别为第1、2振型的阻尼比,对于钢结构近似取为0.02,对混凝土可近似取0.05。
2.2 位移法
结构在外因作用下连续倒塌过程,实际上来说是一个动态的过程,也就是完整结构在使用荷载作用下处于平衡状态,同时产生变形,当外界因素作用使得结构突然失去支撑构件时,结构将会从原来的平衡状态变为不稳定状态,此时结构的变形急增,产生大变形,并最终可能导致结构局部或者整体倒塌,此倒塌过程实际上是一个动态的过程,因此我们常用的静力分析方法在某一种程度上来说是与实际有较大的差异的。从整个倒塌过程来看,结构实际上是在初始位移的状态下发生倒塌,因此要较好的分析结构的倒塌过程首先是要满足结构的初始位移,然后在此条件上采用“抽柱”的方法,让结构突然失去平衡从而达到模拟动态倒塌的效果,当然这种模拟可以通过很多专业的有限元软件来实现,可是专业有限元软件理论较难,操作较复杂,不易被一般工程人员所掌握,在满足工程精度的条件下,考虑使用一般软件来进行结构的动力倒塌分析。因此,为了使大多数工程人员能够进行结构的倒塌分析,本文根据结构倒塌的实际情况,基于sap软件提出了“位移”法,其基本步骤:①对完整结构施加竖向重力荷载,进行静力分析;②对抽掉柱的整体结构施加如图2所示随时间变化的荷载向量(G+0.5LL)进行动力分析,得到结构变形位移以及破坏状态。图2中,tf表示支撑构件失效时间,其取值后面将会进行讨论,另外结构初始位移相对结构倒塌位移来说很小,几乎可以忽略其初始位移的影响,此方法可以进一步简化为结构在初始位移为零的条件下的动态倒塌问题。对倒塌过程中阻尼的确定同样可以采取“反力法”的方法来确定。
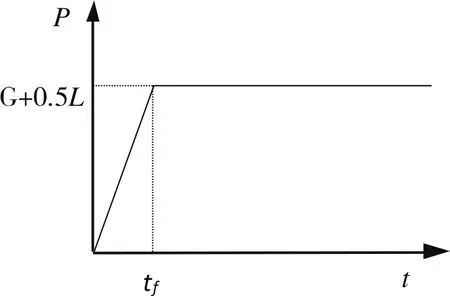
图2 荷载-时间曲线(位移法)
3 两种分析方法的比较
首先建立该框架的sap模型并根据现行规范输入相应荷载,计算得到构件的配筋(图3),整个过程符合我国现行规范的设计要求。然后根据所得到的构件配筋使用位移法对结构进行动态倒塌分析。
3.1 设计参数
本文研究的框架为纵向6跨,横向4跨,共5层的钢筋混凝土框架结构,所有跨度为6 m,层高为3 m,框架梁、柱均为现浇,柱截面尺寸500 mm× 500 mm,纵横梁截面尺寸均为300 mm×700 mm,梁、柱混凝土强度等级均采用C30,纵向受力钢筋选用HRB400,箍筋选用HPB235,梁、柱的布置、配筋如图3所示,混凝土及其钢筋等材料的参数见表1,此模型不考虑楼板的作用,柱脚假设理想固接于地面。

图3 空间框架结构(单位:mm)

表1 材料的计算参数
3.2 分析结果比较
目前虽然较多有限元能够进行结构的动态倒塌分析,但是其操作较为麻烦,后处理也极为不方便,理论也较难,一般设计人员不易掌握,然而“位移法”和“反力法”操作简单,一般设计人员都能很好的应用。本文为了验证位移法的正确性,分别用位移法和反力法对3.1节中的模型进行了动态倒塌分析,并把两者的分析结果进行比较,从而验证位移法的正确性。
图4是采用两种分析方法进行线性动力和非线性动力分析结果,①从线性动力时程分析:位移法和反力法所得到的位移时程曲线有相差较小基本吻合,从分析所得到的加速度时程曲线来看,初始较短时间内位移法所得到的加速度有一定的波动,但是随着时间的增长,两者逐渐趋同。②非线性动力时程分析:位移法和反力法分析所得到的位移时程曲线吻合较好,几乎没有什么差别;从分析所得到的加速度时程曲线来看,同样可以看出结构在初始较短时间内位移法所得到的加速度有一定的波动,但是随着时间的增长,两者逐渐趋同。

图4 位移、加速度时程曲线
4 tf对两种方法分析结果的影响
为了研究柱失效时间tf对两种方法分析结果的影响,论文采用了三个框架模型进行结构的倒塌分析,三个模型的平面布置、梁、柱的配筋以及楼层荷载均同3.1节所示的框架结构,唯一不同的是楼层数,模型A为5层,周期1.0,模型B为8层,周期为1.5,模型C为11层,周期为2.0。对A模型进行了线性和非线性动力分析,对B、C模型只进行了非线性分析,A、B、C模型柱失效时间取值见分析输出曲线,所有模型分析结果见图5、6,图中的位移为柱失效点的时程曲线。

图4 A模型线性分析时程曲线

图6 非线性分析位移时程曲线
图5 为A模型的线性分析时程分析结果,从分析结果来看,不管是位移法还是反力法,如果柱失效时间越短,观测点的位移波动就越大;但是,随着柱失效时间增加,位移波动的幅值减小。而且无论是位移法还是反力法,不管其失效柱时间的长短,其最终位移都将收敛某一定值。图6为A、B、C模型的非线性分析时程分析结果,从分析结果来看,柱失效时间对观测点位移有较大影响,失效时间较短时,观测点位移较大;但是随着失效时间的增加,曲线之间的位移差别就越小。从图中可以看出,结构自身特性对倒塌位移也有影响,对A、B、C模型来说,层数、周期是递增的,不同柱失效时间对观测点位移的影响却是递减的。从图中还可以看出,当三个模型的柱失效时间小于0.15 s时,各失效时间的位移相差较大;当柱失效时间大于0.15 s时,各失效时间的位移随时间的增加逐渐趋同。
5 结论
(1)为研究结构由于柱失效引起倒塌的动力效应,本文采用了“位移法”和“反力法”对失柱的混凝土框架结构进行线性与非线性动力分析,并把位移法与反力法的分析结果进行了对比,分析结果表明在满足工程精度的情况下“位移法”能够较好地进行动力倒塌分析,其操作简单、使用方便、容易被一般工程人员所掌握。
(2)柱的失效时间对“位移法”和“反力法”线性动力分析结果影响较小,随着时间的增大,各失效时间所得到的位移曲线趋同。
(3)柱的失效时间对“位移法”和“反力法”非线性动力分析结果影响较大,柱失效时间较短时,失效时间对位移法和反力法非线性动力分析结果影响大。当柱失效时间小于0.15 s时,各失效时间的位移相差较大;当柱失效时间大于0.15 s时,各失效时间的位移随时间的增加逐渐趋同。
[1]舒赣平,凤俊敏,陈绍礼.对英国防结构倒塌设计规范中拉结力法的研究[J].钢结构,2009,24(6):51-56.
[2]易伟健,何庆峰,消岩.钢筋混凝土框架结构抗倒塌性能的试验研究[J].建筑结构学报,2007,28(5):104-109.
[3]陆新征,李易,叶列平,等.钢筋混凝土框架结构抗连续倒塌设计方法的研究[J].工程力学,2008,5(s):150-157.
[4]王开强,李国强.美国建筑连续性倒塌设计标准的现状[J].解放军理工大学学报,2007,8(5):513-519.
[5]Mehrdad Sasani,Serkan Sagiroglu.Progressive collapse resistance of hotel San Diego.Journal of structural engineering,ASCE,2008,134(3):478-488.
[6]张素芬.钢筋混凝土框架结构抗连续倒塌分析[D].长沙:湖南大学,2008.
[7]林国铎.多高层钢框架结构抗连续倒塌性能分析[D].上海:同济大学,2009.
[8]梁益,陆新征,李易,等.3层RC框架的抗连续倒塌设计[J].解放军理工大学学报,2007,8(6):659-664.
[9]胡晓斌,钱稼茹.多层平面钢框架连续倒塌仿真分析[J].力学与实践,2008,30(4):54-57.
[10]胡晓斌,钱稼茹.单层平面钢框架连续倒塌动力效应分析[J].工程力学,2008,25(6):38-43.
[11]胡晓斌,钱稼茹.多层钢框架连续倒塌动力效应分析[J].地震工程与工程振动,2008,28(2):8-14.
(责任编辑:周晓南)
The Analysis M ethod of Progressive Collapse of Reinforced Concrete Frame Structure
YUAN Bo∗,WANG Xu,CHEN Yao
(Space Structures Research Center,Guizhou University,Guiyang 550003,China)
The"displacementmethod"and"force method"were adopted to carry on the linear and nonlinear dynamic collapse analysis for concrete frame structure with lost column,and the displacementmethod and the force method of analysis results were compared.The results show that both are in good agreement,at the same time linear and nonlinear dynamic calculation methods were used to analyze progressive collapse for the same plan layoutwith differentheight of frame structure and get failure point displacement time-history curve of different column failure time and different period,analysis results indicate:column failure time has almostno effecton results of linear dynamic analysis,with the increase of time,the structural dynamic response tend to converge;column failure time has an effecton results of nonlinear dynamic analysis,butas the failure time increases,structural dynamic response tends to converge.
displacementmethod;forcemethod;progressive collapse;failure time;reinforced concrete frame
TU392
A
1000-5269(2016)04-0095-05
10.15958/j.cnki.gdxbzrb.2016.04.19
2016-03-18
国家自然科学基金项目(51168010)
袁 波(1974-),男,博士(后),副教授,硕导,研究方向:工程防灾减灾,Email:superyuanbo@163.com.
∗通讯作者:袁波,Email:superyuanbo@163.com.

