基于结构风险最小化的TS模糊模型辨识研究∗

刘小雍，周淑芳，熊中刚，陈连贵，阎昌国

(1.遵义师范学院工学院，贵州遵义563002；2.遵义医学院附属医院医学检验科，贵州遵义563003)

基于结构风险最小化的TS模糊模型辨识研究∗

刘小雍1，周淑芳2∗，熊中刚1，陈连贵1，阎昌国1

(1.遵义师范学院工学院，贵州遵义563002；2.遵义医学院附属医院医学检验科，贵州遵义563003)

针对TS模糊模型的后件参数辨识，为了避免传统意义上以经验风险最小化来求解参数，同时考虑到如何控制模型结构复杂性以及经验风险又要最小，提出了一种基于最小二乘支持向量回归(LSSVR)结构风险分解建立新的代价函数来辨识TS模糊模型。紧接着，以该代价函数作为优化目标，TS模糊模型为约束条件，通过引入拉格朗日方法对其求解，最终得到模型的后件参数。该方法有如下显著特征:1)引出的代价函数是基于结构风险而非经验风险;2)计算过程不仅避免了核函数的选择，而且仅对原输入数据空间做内积;3)全局与局部性能得到保证。最后，论证了该方法的有效性和优越性。

结构风险最小化;TS模糊模型;代价函数;辨识

TS模糊模型是一种可以用来表征非线性系统的数学模型，利用这种方法可以将复杂的非线性系统转化为一些简单的线性子系统；此外，该模型还有良好的局部解释能力以及以任意精度逼近非线性系统，所以在非线性系统建模中得到了广泛应用。TS模糊模型[1]是Takagi和Sugeno于1985年提出来的，其模型辨识分为结构辨识和参数辨识两部分，而参数辨识又包括前件参数辨识和后件参数辨识。其中，结构辨识部分得到了大量研究，例如有模糊C均值聚类(FCM)、Gustafson-Kessel聚类算法(GKCA)，减聚类等等；近年来，基于支持向量机(SVM)[2，3]和相关向量机(RVM)[4]方法也被用于TS模糊模型的结构辨识。尽管结构辨识部分得到了广泛研究，然而，却很少有方法提出对TS模糊模型的后件参数辨识部分做进一步研究或改进，仍然用传统的方法进行参数辨识，如最小二乘算法(LS)、正交 LS、递归 LS、期望最大化算法(EM)、和卡尔曼滤波方法等。然而，无论是LS[5]、卡尔曼滤波方法[6]、期望最大化算法(EM)[7]，还是LS及其变体，都是基于经验风险最小化或者局部最优的方法来求解参数，所以会产生模型较差的泛化性能。例如，LS算法，只考虑如何让模型输出与实际输出之间的误差达到最小，而没有考虑如何控制模型结构的复杂性，在这种情况下，训练误差甚至可以达到零，但对测试数据产生很大的偏差，这就意味着最终得到的模型不是所期望的。

对于TS模糊模型，其自身有着较好的解释能力以及以任意精度逼近任意的非线性系统，所以在建模和控制等方面有着广泛的应用。然而，对于模型的后件辨识部分，目前仍采用传统基于经验风险最小化或者局部最优的方法来实现。因此，本文提出基于结构风险最小化的分解，建立TS模糊模型新的代价函数，对后件部分进行辨识。

1 TS模糊模型

一种基于数据的非机理模型，TS模糊模型，通常被用于建模非线性系统模型f(x)。假设获取到测量数据{(x1，y1)，…，(xN，yN)}，N表示测量数据集大小，xi∈Rn，yi为对应的期望输出，则带有R个规则的TS模糊模型为:

Ri表示第i个规则，x1，…，xn是输入变量，Ai1，…，Ain是分配到对应各自输入变量的模糊集〈·，·〉表内积，ai和bi是后件参数，TS模糊模型的最终输出为:

其中:

φi(x)表示第i个规则的标准触发强度，μij(x)描述的是模糊集Aij的隶属函数。

考虑到模糊Gustafson-Kessel聚类算法(GKCA)主要是基于其聚类协方差矩阵的特征值提供了关于聚类形状和方向的相关信息，可以检测到带有不同形状和方向的整个数据集的类，因此，在TS模糊模型结构辨识部分将采用GKCA方法。

2 结构风险分解下的TS模型辨识

通过对基于LSSVR模型的结构风险进行分解，建立新的带有结构风险特性的代价函数来对TS模型的后件参数进行辨识，从而达到建模TS模糊模型，其简要流程如图1所示。

图1 建立TS模糊模型的简要流程图

2.1 一种基于结构风险分解的新代价函数

基于TS模糊模型将其展开为:

定义，

对于TS模型，则有:

根据规则数R，LSSVR也可进行R项分解:

因此，基于LSSVR的原始优化问题可进一步转化成:

模型结构与数据拟合之间的相对重要性由规则化常量γVR来决定。从式(6)和(7)，可进一步得到TS模型后件参数的代价函数:

考虑到TS模糊模型的前件结构部分被确定之后，意味着标准化后的触发强度值φk(x)在最小化J1的过程中被确定，所以式 (9)可以变成如下形式:

因此，最小化TS模糊模型的代价函数被建立。

2.2 基于代价函数的TS模型辨识

在最小化TS模型所对应的代价函数时，其满足的约束条件跟LSSVR一样，仅仅约束中的模型发生了变化。求解一阶TS模糊系统后件参数所对应的优化问题给定为:

应用拉格朗日方法，上述优化问题被构造为:

αi∈R表示拉格朗日乘子。根据KKT优化条件:

此外，在式(13)中，向量αk的分量αjk按下式可计算为:

将式(18)带入式(20)得:

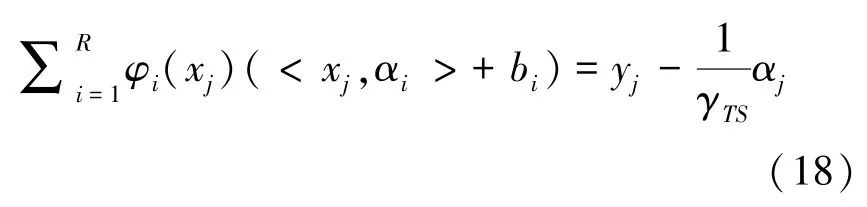
再将式(14)代入式(16)有:

从式(13)和式(15)，进一步得到:

其中:

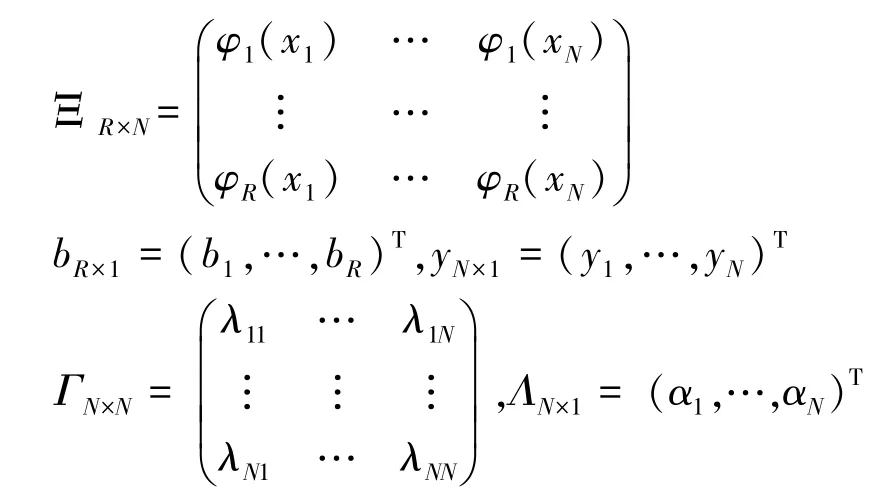
关于矩阵ΓN×N里面的元素λij计算为:

从上式的计算可知，元素λij计算不涉及核函数的选择，同时仅仅对原数据空间做内积即可，且矩阵ΓN×N是对称矩阵。

对拉格朗日乘子的计算，可以根据式(20)有:

因此，拉格朗日乘子向量ΛN×1被计算为:

最终，由式子(17)可得TS模糊系统的后件参数被求解。

对所提出方法的建立过程如图2所示。

图2 提出方法的建立过程

可以将其主要归述为，第一步设定聚类规则数，然后根据聚类规则数R，对LSSVR的回归模型进行R项分解，这里的分解主要是基于某个向量，该向量总可以分解为R项具有相同维数的向量之和。同时，TS模糊模型也可进行R项展开并作部分变量代换处理，得到LSSVR回归模型和TS模型具有等价的模型描述形式；紧接着，对基于LSSVR的结构风险同样进行R项分解，得到分解后的结构风险。考虑到经过处理之后的这两种模型在描述形式上相同的，因此，结合分解后的结构风险，最终建立基于TS模糊模型的一种新的代价函数。通过代价函数和以TS模糊模型为约束条件建立拉格朗日函数并结合KKTr优化条件，最终求解出模型的后件参数。

3 仿真论证

这部分主要通过仿真对提出的方法进行论证，所使用的性能评估指标是均方误差(Measure Squares Error，MSE)，定义如下:

其中N表示测试数据集的大小，yk表示实际的数据，是TS模糊模型的预测输出。

首先考虑用于逼近非线性函数的一个简单问题如下:

图3 使用提出的方法建模非线性函数

其中v表示均值为0，方差为0.1的白噪声，x的取值范围是[0 120]。在仿真过程中，将取值范围等间隔取值，产生1201个训练数据点。通过应用提出的方法后，可得TS模糊模型的后件参数，如表1所示，同时也包括文献[8]使用传统的最小二乘算法(LS)以及卡尔曼滤波方法辨识TS模糊模型时的后件参数，以及它们所对应的MSE。基于提出方法得到的一阶TS模糊模型的输出与非线性函数的输出如图3所示。从图表结果可以清楚地看到，通过提出的方法所建立的TS模糊模型有较好的性能。

表1 TS模糊模型的后件参数及MSE比较

下面考虑双输入单输出的一个仿真，其模型是来自文献[9]的静态非线性函数作为新的研究对象，然后用提出的方法来对其进行建模。双输入单输出的非线性函数:

其中两个输入变量的范围定义在区间1≤x1，x2≤5，且两个变量在区间上使用等间隔采样，然后从式(26)获取50个数据用于建模TS模糊模型。

在建模TS模糊模型的过程中，其前件部分语言输入变量选择x1和x2，结构辨识部分采用前面介绍的模糊Gustafson-Kessel聚类算法；对于后件参数部分，使用提出的方法进行辨识。在选择相同规则数R为6，10，25的情况下，表2给出了提出方法与其他文献[9-11]的MSE比较结果。图4给出了在规则数R选择为25的情况下得到的仿真曲线。接下来考虑如下的非线性动态系统:

表2 双输入单输出的非线性函数的MSE结果比较

图4 使用提出的方法建模非线性函数

其中noise表示均值为0，方差是0.25的高斯白噪声。基于上式产生501个训练数据，通过应用提出的方法，非线性动态系统的实际输出与预测输出及误差分别如图5和图6所示。

同时给出了与其他不同方法的性能比较，如表3所示。

表3 不同方法对非线性动态系统建模的MSE比较

图5 提出的方法对非线性动态系统的辨识

图6 模型预测输出与实际输出的预测误差

4 结论

目前，TS模糊模型在结构辨识上得到广泛研究，却很少在参数辨识上做进一步研究，仍然采用传统的经验风险、局部最优等方法对参数进行辨识，例如最小二乘算法及其辩题、期望最大化算法等。因此，提出了一种基于结构风险最小化的新代价函数辨识TS模糊模型的后件参数，以该代价函数作为目标，TS模型为约束条件，应用KKT优化条件对其求解。尽管引入了LSSVR的相关知识，但在计算过程中不涉及核函数选择，其运算主要是对原数据空间做内积即可，并没有涉及高维数据的运算。最后，通过静态模型、多输入单输出以及非线性动态系统模型对提出的方法进行了论证。

[1]Takagi T，Sugeno M.Fuzzy identification of systems and its applications tomodeling and control[J].Systems，Man and Cybernetics，IEEE Transactions on，1985，15(1):116-132.

[2]ZhaoW，Zhang J，Li K.An Efficient LS-SVM Based Method for Fuzzy System Construction，IEEE[J].Transactions on Fuzzy Systems，2015，23(3):627-643.

[3]梁炎明，苏芳.基于支持向量机回归的TS模糊模型自组织算法及应用[J].自动化学报，2013，39(12):2143-2149.

[4]Kim J，Suga Y，Won S.A new approach to fuzzymodeling of nonlinear dynamic systemswith noise:relevance vector learningmechanism[J].Fuzzy Systems，IEEE Transactons on，2006，14(2): 222-231.

[5]Mendonca L F，Sousa JM C，Costa JM G S.An architecture for fault detection and isolation based on fuzzy methods[J].Expert Systemswith Applications，2009，36(2):1092-1104.

[6]郭颖，吕剑虹，吴波，等.基于TS模糊模型的热工过程建模方法[J].系统仿真学报，2010(01):210-215.

[7]Wang L，Langari R.Sugenomodel，fuzzy discretization，and the EM algorithm[J].Fuzzy Sets and Systems，1996，82(3):279-288.

[8]Chafaa K，Ghanai M，Benmahammed K.Fuzzy modelling using Kalman filter[J].Control Theory＆Applications，IET，2007，1 (1):58-64.

[9]Sugeno M，Yasukawa T.A fuzzy-logic-based approach to qualitativemodeling[J].IEEE Transactions on fuzzy systems，1993，1 (1):7-31.

[10]Nozaki K，IshibuchiH，Tanaka H.A simple but powerful heuristic method for generating fuzzy rules from numerical data[J].Fuzzy sets and systems，1997，86(3):251-270.

[11]Lee S J，Ouyang C S.A neuro-fuzzy system modeling with selfconstructing rule generationand hybrid SVD-based learning[J]. Fuzzy Systems，IEEE Transactions on，2003，11(3):341-353.

[12]Chuang，C.-C..Fuzzy weighted support vector regression with a fuzzy partition[J].IEEE Trans.Syst.Man Cybern.B，Cybern，2007，37(3):630-640.

(责任编辑:曾 晶)

Research on Identifying TS Fuzzy M odel Based on Structural Risk M inim ization

LIU Xiaoyong1，ZHOU Shufang2∗，XIONG Zhonggang1，CHEN Liangui1，YAN Changguo1

(1.College of Engineering and Technology，Zunyi Normal College，Zunyi 563002，China；2.Department of Laboratory Medicine，Affiliated Hospital of ZunyiMedical College，Zunyi 563003，China)

Aiming at the consequent parameters of the TS fuzzymodel，a novel cost function based on decomposing LSSVR was proposed to identify consequent parameters，which makes use of the structural risk considering how to control the trade-off between empirical risk and model complexity instead of the conventional empirical risk.And then，a new optimization problem was formulated by treating the obtained cost function as the objective function，TS fuzzymodel as constraint condition，and the consequent parameters of TS fuzzymodelwere derived by applying Lagrangemethod.The resultingmethod has the following distinct features:(1)the obtained new cost function can be regarded as a structural risk instead of empirical risk；(2)the computation process cannot only avoid the selection of kernel function，but alsomerely use the scalar product for original input space；and(3) the approach can well guarantee the performance of both local-regression models and globalmodel.Finally，the viability and superiority of themethod were verified by simulation.

structural risk minimization；TS fuzzymodel；cost function；identification

TP391.9

A

1000-5269(2016)04-0064-05

10.15958/j.cnki.gdxbzrb.2016.04.13

2016-02-19

贵州省教育厅项目(黔教合KY字[2015]457号)；省科技厅项目(黔科合LH字[2015]7054号，黔科合LH字[2016]7018号)；遵义师范学院博士项目(遵师BS[2015]04号)

刘小雍(1982-)，男，副教授，博士，研究方向:机器学习、数据-模型融合建模以及状态/参数估计等，Email:liuxy204＠163.com.

∗通讯作者:周淑芳，Email:springzhousf＠163.com.