浅谈教科书拓展性内容的结论在解题中的应用>——以人教A版高中《数学(选修2-1)》为例
秦晓燕
(河南省漯河高中,漯河 462000)
浅谈教科书拓展性内容的结论在解题中的应用
>——以人教A版高中《数学(选修2-1)》为例
秦晓燕
(河南省漯河高中,漯河 462000)
近几年数学高考的命题已经越来越多地来源于教科书,有些命题是教科书例题或习题的变式,有些命题能运用教科书中例题或拓展性内容的结论简化解题过程.因此,在教学中,教师应以教科书为蓝本,让学生把教科书中的问题彻底学懂、学透,不仅要会解、会证明,还要能举一反三、灵活运用.本文,笔者以人教A版高中《数学(选修2-1)》为例来谈谈拓展性内容的结论在解题中的应用.
应用1 椭圆、双曲线定义相关结论的应用
【教科书链接1】(第41页例3)


图1

图2
【教科书链接2】(第55页探究)

深挖教科书,我们可以将上面两题拓展到一般情况,从而得出了以下两个结论.接着我们就利用这两个结论来解题.





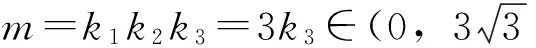


【答案】B
【解析】如图3,由题知C(1,0),A1(-2,0),A2(2,0).

图3
设B1(1,y1),B2(1,y2)(y1>0,y2<0).
∴S△A1B1C=S△A2B2C.
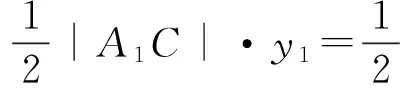
即 3y1=-y2.
①
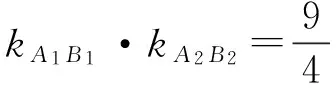

②

【点评】在求解这两道例题时,如果运用了上面双曲线定义的相关结论,就可以大大减少运算量,这对解答高考题中的选择、填空题能起到事半功倍的效果.
应用2 截口曲线是椭圆相关结论的应用
【教科书链接】(第42~43页)
如图4,用一个平面去截圆锥,得到的截口曲线是椭圆.那么,为什么截口曲线是椭圆呢?

图4
历史上,许多人从纯几何角度出发对这个问题进行过研究,其中数学家Germinal Dandelin的方法非常巧妙.
在圆锥内放两个大小不同的球,使得它们分别与圆锥的侧面、截面相切.两个球分别与截面相切于点E,F,在截口曲线上任取一点A,过点A作圆锥的母线,分别与两个球相切于点C,B.由球和圆的几何性质,可以知道
AE=AC,AF=AB.
于是
AE+AF=AB+AC=BC.
由切点B,C的产生方法可知,它们之间的距离BC是定值.这样,截口曲线上任意一点A到两个定点E,F的距离之和为常数.
由椭圆的定义可知,截口曲线是椭圆.
我们仿照上面这个问题的证明过程不难得出以下的结论,接下来我们再利用这个结论解题.
结论 用一个与圆柱的母线斜交的平面截圆柱,得到一条截口曲线也是椭圆.

图5
【考题链接】例3 (2016 河南省漯河高中4月模拟)如图5所示,一个圆柱形乒乓球筒,高为20 cm,底面半径为2 cm.球筒的上底和下底分别粘有一个乒乓球,乒乓球和球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
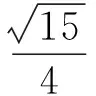

【答案】A

图6
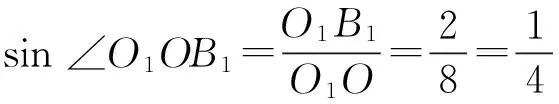
又由于O1O∥A1H,所以△O1OB1∽△OA1H,其中∠O1OB1=∠OA1H,

而乒乓球的直径为椭圆的短轴长,2b=2r=4,即b=2.

【点评】本题中的一个平面与两个乒乓球均相切,此平面截球筒边缘所得的图形为一个椭圆,在此背景下求椭圆的离心率,难度较大.解题的关键是求出椭圆的长轴长A1A2,短轴长2r=4;通过两个相似的直角三角形建立角和边长关系,从而求得了a=8. 在解题时,一定要明白三类接触点A1和A2、B1和B2、C1和C2是不重合的.
应用3 圆锥曲线的光学性质的应用
【教科书链接】( 第75~76页)
抛物线有一条重要性质:从焦点发出的光线,经过抛物线上的一点反射后,反射光线平行于抛物线的轴,如图7.

图7
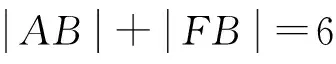
【答案】y2=4x

【点评】本题的解决方法是建立在光学的一条重要性质的基础上,而这条性质在教科书中是属于阅读材料的内容,命题人认为这是一个常识,学生应该掌握. 但事实上,不少学生根本就不了解这个常识,觉得这道题缺少条件,殊不知,是自己忽视了教科书中的知识点.
由此我们发现教科书中的探究性内容实用性很强,既在基础知识上进行了拓展,又突出了数学知识与时代发展
的联系.探究性内容引导了学生主动去思考,并对所学的知识举一反三.不仅考虑了学生数学发展的不同需求,还为不同的学生提供了适合自己的发展空间.因此教师在教学中应重视教科书中的探究性内容的学习,并把它们都分析透彻,掌握清楚.
随着社会的进步和文化的发展,教师和学生手中有着越来越多的教学资源和复习资料.于是不少学生甚至教师都丢掉了教科书,整天埋在参考资料中.而事实上,教科书才是根本,才是精髓,只有先学透了,才能在此基础上举一反三,向更深层次发展.作为高中的数学教师,我们应让学生先吃透教科书中的基础知识,把其中的定义、性质定理及其证明都搞清楚,然后再把相应的例题、结论、课后作业、阅读材料等拓展性内容进行整合并牢牢掌握.只有先把基础知识学扎实了,才能更好地去运用相关参考资料加深和巩固.这样,学生的眼界拓宽了,从中体会到了数学的魅力和价值,就能更自主地学习数学.
人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书数学(选修2-1 A版)[M]. 北京:人民教育出版社,2013.
(责任编辑:李 珺)

