不同参数的不对称阶梯型量子阱等离激元特性研究

宋亚峰，朱勤生，孔雄雄，焦壮壮

(1. 商洛学院电子信息与电子工程学院物理系，陕西 商州 726000； 2. 中国科学院半导体研究所材料重点实验室，北京 100083)



不同参数的不对称阶梯型量子阱等离激元特性研究

宋亚峰1，朱勤生2，孔雄雄1，焦壮壮1

(1. 商洛学院电子信息与电子工程学院物理系，陕西 商州 726000； 2. 中国科学院半导体研究所材料重点实验室，北京 100083)

用无规相近似的二子带模型，系统研究了阶梯层宽度、深阱宽度、阶梯层的Al组分(阶梯层势垒的高度)对AlGaAs/GaAs不对称阶梯型量子阱中准二维电子气的等离激元特性的影响。发现子带间等离激元模的能量大小取决于基态和第一激发态的能级差，而模的长短取决于这两个能级波函数的交叠大小。这些结论可能为研究空间不对称效应对准二维电子气特性的影响以及基于阶梯型量子阱结构的器件应用等方面提供有益的参考。

等离激元；集体激发；不对称阶梯型量子阱；结构参数

0 前 言

近年来，低维电子系统中的集体激发特性(等离激元)是固体中一个有趣而重要的研究课题，在实验[1-6]和理论[7-12]上都取得了广泛的研究成果。其中，准二维电子气系统中电子的集体激发特性是研究热点之一，他不仅是二维电子气系统的基本特性的重要方面之一，而且有很大的应用前景。即使是少数的涉及空间不对称效应对集体激发特性影响的研究中，他们所考虑的空间不对称效应大多集中在不对称双量子阱结构中[8]。

然而，据我们所知，另一种准二维集体激发中的空间不对称特性还没有被系统研究过，这就是：不对称阶梯形量子阱中的不对称效应。通过在垒层和阱层之间插入一层台阶层，就形成了所谓的阶梯形量子阱。他具有区别于对称单量子阱的许多有趣而独特的优点，例如：具有相同奇偶性量子数子带间的跃迁通常是禁戒的，此时却变得允许了[11]；大的Stark效应[12]；大的振子强度；大的二次谐波非线性效应；更低的阈值泵浦功率等等。所有这些独特的优点，使阶梯阱结构最近越来越多地被人们用于各种半导体器件的设计应用上。鉴于不对称阶梯形量子阱结构有这么多的优点以及以上人们已知的传统的双量子阱和单量子阱中各种不同的等离激元特性，我们可以合理地预测，在电子集体激发特性方面，这种很有应用前景的阶梯阱结构中可能有一些独特的容易控制的等离激元特性。

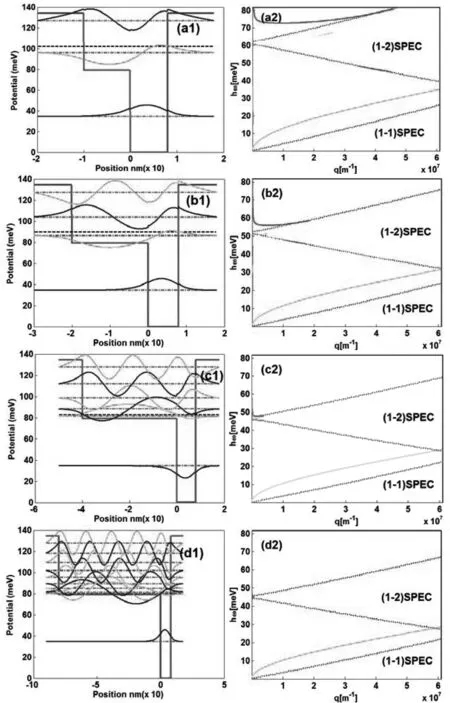
出于以上考虑，我们研究了AlxGa1-xAs/AlyGa1-yAs/GaAs/AlxGa1-xAs(y

1 理论模型

我们研究的不对称阶梯形量子阱，阶梯型量子阱的结构和能级波函数形貌图(左图)及相应的电子集体激发色散关系图(右图)如图1所示，a～d分别表示台阶层宽度为10，2，40,80 nm。他包含了一个宽度为d的GaAs深阱层，一个宽度为s、势垒高度为Vs的AlyGa1-yAs阶梯层，以及两边两个势垒高度为Vb的AlxGa1-xAs势垒层。在有效质量近似下，电子在不对称阶梯形量子阱中的行为可以由单电子一维薛定谔方程来描述：

(1)

其中V(z)是图1和2插图所示的不对称阶梯形量子阱各处的导带底的电势能的形貌。对于特定Al摩尔组分x的阶梯阱，数值求解方程1就可得到

图1 阶梯型量子阱的结构和能级波函数形貌(左)及

其对应的本征能量和本征波函数。这里，我们采用了公式△Ec(x)=0.79x(eV)[适用于x<0.41]来计算Al摩尔组分x所对应的导带底带阶差。对于AlxGa1-xAs材料的其他参数，我们分别采用了：有效质量m*/m0=0.066 5+0.100 6x+0.013 7x2和低温下静电相对介电常数εr=12.4-1.8x[3]。

此外，众所周知，无规相近似(RPA)是一个计算等离激元非常经典的模型，他在计算好多情况下电子的元激发谱中都是非常精确的，甚至在高的电子密度下[6]。所以此处我们将无规相近似理论模型用于我们不对称阶梯形量子阱中等离激元的计算中。这是一个很合理的近似。同时考虑到本文中讨论的大多数等离激元的能量并不接近于LO声子的能量(对于GaAs是36 meV)，我们忽略了等离激元和LO声子的耦合作用。同时据文献[4]估计，GaAs/AlGaAs系统中的类激子效应是比较小的，所以我们忽略了该效应。此外由文献[5]得知，交换关联效应、能带弯曲效应和镜像效应同样很小以至于可以忽略，而我们此处重点考察的是阶梯阱中不对称效应对等离激元的影响，所以这几种效应此处也忽略了。根据无规相近似和线性响应理论[6]，动态介电函数的表达式为：

εijmn(q，ω)=δimδjn-Vijmn(q)Πmn(q,ω)

(2)

其中：

Vijmn(q)=∫dz∫dz′Ψi*(z)Ψj(z)V0(q,z,z′)Ψm*(z′)Ψn(z′)

(3)

(4)

此处Π是林哈德函数， hω+≡hω+iγ其中γ→0，而且阶梯阱中库仑相互作用的二维傅里叶变换为

(5)

det|εijmn(q,ω)|4×4

(6)

因此下一节中，我们将给出各种不同种类不对称结构的阶梯阱将会给等离激元模的带来不同类型的改变。

2 结果和讨论

基于以上模型，我们分别计算了各种不同类型的阶梯型不对称量子阱的量子结构，尤其是重点系统分析了台阶阱宽度、深阱宽度、台阶阱的Al组分(台阶的高度)的变化对等离激元色散关系特性的影响作用。

2.1 随台阶阱宽度变化的等离激元色散关系

阶梯型量子阱的的其他参量保持不变，由图1对比可以发现：随着阶梯层宽度的增大，位于深阱中的基态能级位置几乎不变，而激发态能级间距越来越小。对应的色散关系，随着阶梯层宽度的增大，子带内等离激元模和单粒子激发区几乎不变，变化最大的是子带间等离激元模变得越来越小，但能量位置基本不变。换句话说，就是子带间等离激元模的色散关系的波矢范围越来越小，而能量几乎不变。这是由于随着阶梯层宽度的增大，基态和第一激发态的波函数交叠越来越小，而能级间距几乎不变。

2.2 随深阱宽度变化的等离激元色散关系特性

图2a～e分别为深阱层宽度为2，4，16，20，40 nm时阶梯型量子阱的结构和能级波函数形貌(左)及相应的电子集体激发色散关系(右)。

图2 阶梯型量子阱的结构和能级波函数形貌(左)及

阶梯型量子阱的的其他参量保持不变。对比图2可以发现：随着深阱层宽度的增大，深阱中的能级的数目分别经历了0，1，2，3个…到很多个的转变。对应的色散关系，随着深阱层宽度的增大，子带内等离激元模和单粒子激发区几乎不变，而子带间等离激元模的能量和波矢都有很大变化。而且变化的趋势比较复杂：能量先增大后减小，波矢先变短后又变长。这是由于随着深阱层宽度的增大，深阱中的能级的数目从无到有，从少到多。基态和第一激发态的能级间距从小变大，再从大变小，而二者的波函数交叠则是从大变小，然后再从小变大。

2.3 Al组分变化的等离激元色散关系

图3a～e分别为台阶阱的Al组分0.01、0.02、0.04、0.1、0.14时阶梯型量子阱的结构和能级波函数形貌(左)及相应的电子集体激发色散关系(右)。

图3 阶梯型量子阱的结构和能级波函数形貌(左)

阶梯型量子阱的的其他参量保持不变。对比可以发现，随着台阶阱的Al组分的增大，阶梯层势垒高度增大，基态能级缓慢升高，而激发态能级迅速升高。对应的色散关系，随着阶梯层宽度的增大，子带内等离激元模和单粒子激发区仍然几乎不变，而子带间等离激元模的长度先变小后又明显变大，但能量单调增大。这是由于随着台阶阱的Al组分(阶梯层势垒高度)的增大，基态和第一激发态的能级间距单调增大，而二者波函数交叠先变小后变大，波函数交叠的最小情形出现在基态在深阱中，第一激发态还在大阱中的时候。

总结以上3种情况发现：对于阶梯型量子阱中电子集体激发的等离激元模，子带间等离激元模的能量大小取决于基态和第一激发态的能级差，而模的长短取决于这两个能级波函数的交叠大小；而子带内等离激元随结构变化不敏感。

3 结 论

我们用Bohm-Pine的无规相近似的二子带模型，研究了AlGaAs/GaAs不对称阶梯形量子阱中等离激元的色散关系。通过系统地调整阶梯阱各层的厚度和Al的合金组分，我们发现：子带间等离激元模的能量大小取决于基态和第一激发态的能级差，而模的长短取决于这两个能级波函数的交叠大小；而子带内等离激元随结构变化不敏感。通过调节深阱的宽度，可以很灵活方便地控制子带内和子带间集体激发模之间的耦合与非耦合。这些阶梯阱中等离激元模的特性可能为研究空间不对称效应对准二维电子气系统中的集体激发特性的影响以及基于阶梯阱的器件应用等方面提供有益的参考。

[1] Jain J K, Sarma S D. Elementary electronic excitations in a quasi-two-dimensional electron gas[J]. Phys. Rev. B, 1987(36): 59491-59495.

[2] Wendler L, Kraft T. Dynamical response of double parabolically graded quantum wells[J]. Phys. Rev. B, 1996(54): 11436-11440.

[3] Mishchenko E G, Peizer M Y, Glazman L I. Plasmon attenuation and optical conductivity of a two-dimensional electron gas[J]. Phys. Rev. B, 2004(69): 195302-195306.

[4] Liu D F, Lin Y X. Doping dependence of electron populations in optically pumped step quantum well structures[J]. Semicond. Sci. Technol., 2011(26): 025002-025007.

[5] Decca R, Pinczuk A, Wet K W. Absence of spin-density excitations in quasi two-dimensional electron systems[J]. Phys. Rev. Lett., 1994(72): 1506-1510.

[6] Li Q P, Sarma S D, Joynt R. Elementary excitations in one-dimensional quantum wires: Exact equivalence between the random-phase approximation and the Tomonaga-Luttinger model[J]. Phys. Rev. B, 1992(45): 13713-13718.

[7] Li Q P, Sarma S D. Elementary excitation spectrum of one-dimensional electron systems in confined semiconductor structures: Zero magnetic field[J]. Phys. Rev. B, 1991(43): 11768-11772.

[8] Liu X H, Wang X H, Gu B Y. Effects of interwell coupling on plasmon modes in symmetric double square quantum well structures[J]. Phys. Rev. B, 2001(64): 195322-195326.

[9] Tselis A C, Quinn J J. Theory of collective excitations in semiconductor superlattice structures[J]. Phys. Rev. B, 1984(29): 3318-3322.

[10] Grosu I, Tugulan L. Plasmon dispersion in quasi-one-and one-dimensional systems with non-magnetic impurities[J]. Physica E, 2008(40): 474-477.

[11] Mii Y J, Wang K L, Yuh P F. Observation of large oscillator strengths for both 1→2 and 1→3 intersubband transitions of step quantum wells[J]. Appl. Phys. Lett., 1990(56): 1046-1049.

[12] Mii Y J, Karunasiri R P G, Yuh P F. Large Stark shifts of the local to global state intersubband transitions in step quantum wells[J]. Appl. Phys. Lett., 1990(56): 1986-1990.

Plasmon Characteristics of Different Structure Parameter Dependence in AlGaAs/GaAs Asymmetric Step Quantum Wells

SONG Yafeng1, ZHU QinSheng2, KONG Xiongxiong1, JIAO Zhuangzhuang1

(1.ElectronicInformationandElectricalEngineeringCollege,ShangluoUniversity,Shangzhou,Shanxi726000,China; 2.KeyLaboratoryofSemiconductorMaterialsScience,InstituteofSemiconductors,ChineseAcademyofSciences,Beijing100083,China)Abstract:We have investigated the different structure parameter dependence of plasmon characteristics in AlGaAs/GaAs asymmetric step quantum wells (ASQWs) within the framework of random-phase approximation in two-subband model.By adjusting the thickness of the step layer, the thickness of the well layer and the Al content of the step layer, we have found that the energy of the intersubband plasmon that depends on the energy difference of the ground state and the first state, while the length of the mode depends on the overlap level of the wavefunctions of the two states. These characteristics can provide useful references for the asymmetric effects on the properties in quasi-two-dimensional system for the application-oriented ASQWs device structures.

Plasmons; Collective excitations; Asymmetric step quantum wells; Structure parameters

2016-11-10

国家自然科学基金项目(Nos. 61076001和10979507)；商洛市科技局科研计划项目(SK2015-35)；商洛学院科研项目(15SKY025)

宋亚峰(1984-)，男，山西介休人，讲师，博士，研究方向：半导体低维量子物理与器件，手机：17789258945，E-mail：cumtsyf03@163.com.

O572.2

A

10.14101/j.cnki.issn.1002-4336.2016.05.050