异步电机定子模态分析

刘丹仲

(上海交通大学机械与动力工程学院,上海 200240)



异步电机定子模态分析

刘丹仲

(上海交通大学机械与动力工程学院,上海 200240)

定子模态分析是异步电机设计的重要步骤。本文利用有限元法建立了型号为YXKK710-6TH电机定子的有限元模型，并对此电机定子进行模态分析，得出了定子的理论固有频率，同时对该型号的电机定子进行了定子模态测试，结果表明：分析结果与实测结果基本接近。相关研究结论为电机的整体结构设计及振动特性分析提供了有益的参考。

异步电机 定子 模态分析

0 引言

异步电动机具有系统简单，安装周期短，启停方便，运行经济，可靠性高，维护检修方便等突出优点，长期以来都是作为工业系统中的主要动力设备，其功率消耗占所有工业设备消耗的70%左右。近年来，市场对异步电机的振动和噪音考核要求越来越严格，由于中心高在560mm以上的异步电动机工作噪音一般都在85dB(声压级)以上，因而降低此类大型电机运转的噪音刻不容缓。而要准确知道异步电动机产生的振动和噪声，则需要研究电机定子模态及其响应特性。目前国内外不少学者已做过类似研究。谢颖、刘海松和刘海东等人利用三维建模软件和ANSYS分析工具，建立型号为Y802-2异步电机的电磁场分析模型，列出了电机的整体振型[1]；佟宁泽利用解析法对型号为YKK500-4异步电机也建立了类似的电磁场模型，得到了气隙磁密分布图，研究了不同定转子槽配合对径向电磁力的影响，计算得出了该电机定子的共振频率[2]；王玎、祝长生和符嘉靖则采用了ANSOFT软件建立了某异步电机定子谐响应分析模型，获得了定子在时域上的径向力波，最后用ANSYS软件对原模型进行修正，成功降低了该电机的噪声[3]；国外的S.C.Chang和R.Yacamini通过初步研究某台异步电机机座和定子铁心的频响特性，得出了定子结构中若存在不规则和不对称结构，则会产生一个特定的圆形振型，并导致增大电机的振动和噪声的结论[4]；Gray则对某个大型电机的定子铁心叠片结构进行了详细的频谱分析[5]；Z.Tang、P.Pillay以及K.N.Srinivas、R.Arumugam等人分别介绍杨氏模量在定子振动特性研究中的重要性和定子绕组对共振所产生的效果和作用[6][7]。

本文以YXKK710-6TH电机定子为对象，对其进行模态分析与试验，为电机进一步的振动特性分析提供依据。

1 模态分析原理

模态分析的实质就是坐标变换，目的是将相应向量从物理坐标系转换到模态坐标系中进行表达，简而言之，模态分析就是求解系统的固有频率和固有振型。经典力学理论指出研究对象的动力学通用方程为：

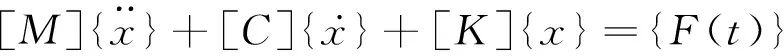
(1-1)

式中：

[M]—质量矩阵，

[C]—阻尼矩阵，

[K]—刚度矩阵，

{x}—位移矢量，

{F(t)}—载荷矢量。

模态分析问题属于无阻尼自由振动问题，可以忽略所有阻尼和载荷，即[C]=0和{F(t)}=0，因此，方程(1-1)可表示为：

(1-2)

根据微分方程理论可知{x}=ejωt{φ}，因此，方程(2.2)可表示为：

([K]-ω2[M]){φ}ejωt=0

(1-3)

式中：

Ω—固有频率，

{φ}—固有振型。

根据线性方程组理论，方程(2-3) 存在非零解的充要条件是：

|[K]-ω2[M]|=0

(1-4)

求解方程(1-4)得到振动系统的固有频率，然后将固有频率代入方程(1-3)得到振动系统相应的主振型向量，主振型向量经归一化处理后得到固有振型。

2 电机定子有限元模型

型号为YXKK710-6TH的电机外形图见图1，其主要设计技术参数见表1，定子主要结构参数见表2。

(1) 建立几何模型

首先分析该电机的零部件组成，在SolidWorks软件的零件模块中建立电机的零部件，并对其进行几何简化；再在SolidWorks软件的装配模块中将这些零部件组装成完整的电机装配体。如图2所示。

图1 YXKK710-6TH电机Fig.1 The motor(type：YXKK710-6TH)

表1 电机主要技术参数Table 1 Main technical parameters of electric machine

表2 定子主要结构参数Table 2 Main structural parameters of stator

(2) 建立有限元模型

1) 定义单元类型

单元类型对有限元分析结果的准确性有很大的影响，单元类型的选择需充分考虑产品的材料特性和所进行的分析类型。本文选择Plane 42单元和>Solid 45单元。

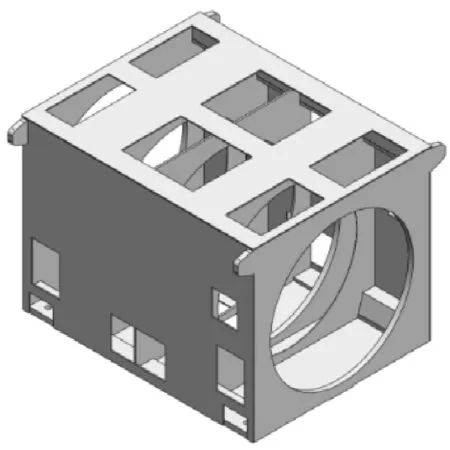
(a) 机座

(b) 定子铁心

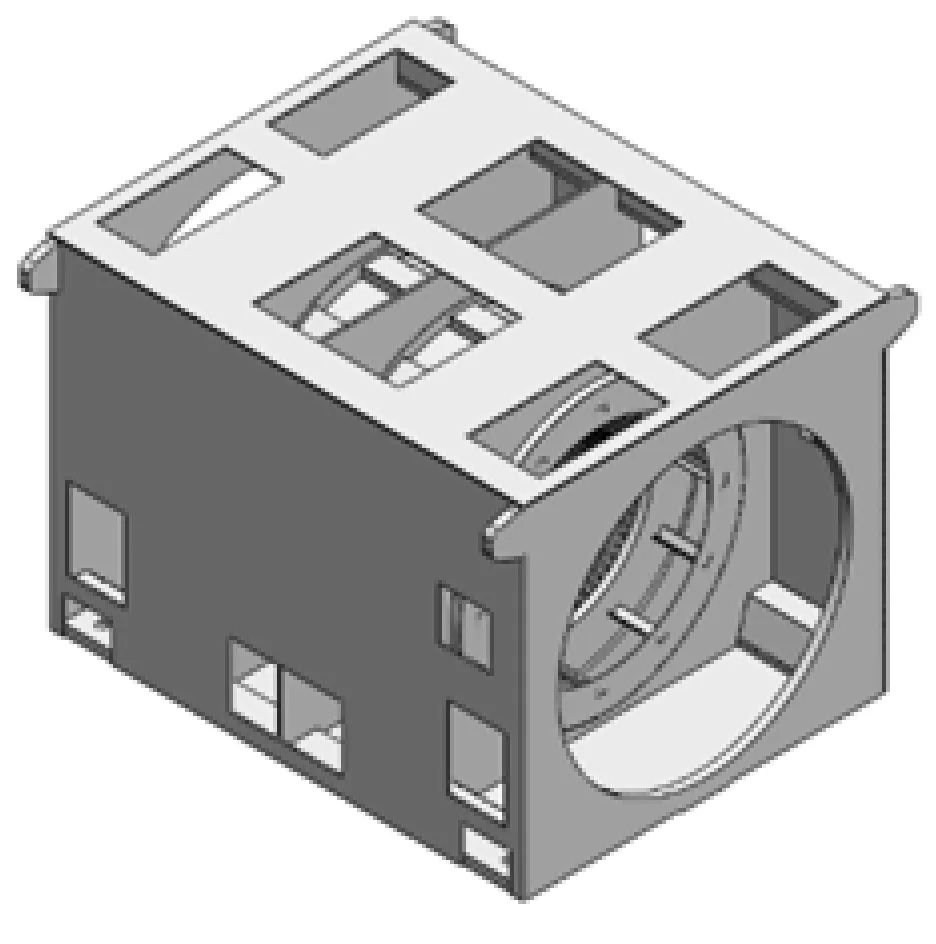
(c) 定子(无端盖)

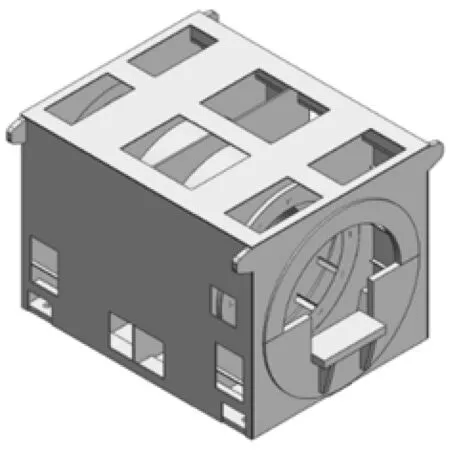
(d) 定子(带端盖)

2) 定义材料特性

只有合理地定义材料特性，才能得到可靠的分析结果。一般的结构分析需要定义材料的弹性模量、泊松比和密度等属性。根据功能需要，大型电机各部件由不同材料制成，包括Q235、硅钢50W400、绕组铜等。定子铁心是由大量硅钢冲片叠压而成，在实际理论分析中通常将铁心作整体化处理。图3为电机实际定子组成情况，表3所示为经过等效处理后的电机定子系统模态分析所需材料的特性。

(a) 机座

(b) 定子铁心

(c) 定子绕组

(d) 端部压圈

(e) 内部通风槽板

(f) 挡风圈

3) 划分网格

一般情况下，模态分析对网格划分没有特殊的要求，因此，在保证分析结果精度的前提下，采用自由划分方法对电机定子进行网格划分。图4为定子模态分析所需的部分有限元模型。

3 定子系统模态分析

定子系统由定子铁心、机座、绕组等多部分装配而成，对其进行模态分析时需根据装配关系和约束条件进行有效的连接关系处理，否则孤立的零部件不能形成相互间的联系。由于ANSYS默认不设置相接触的零部件间接触面的类型，逐一对其进行装配接触面的设置比较困难。这里采用Glue粘结法将各个组成部分进行粘结。

1) 加载和求解

定子系统的约束是通过四个螺栓孔与基础底架进行连接固定的，因而将这四个螺栓孔的内表面设定为固定面即可。同样也是为了与实际安装情况相吻合，也要将机座安装板的下表面也设定为固定面。此外，不对定子系统施加位移约束以外的载荷。选用Block Lanczos法进行求解，并设置模态提取和模态扩展数目为100。

(a) 机座

(b) 定子铁心

(c) 定子(无端盖)

(d) 定子(带端盖)

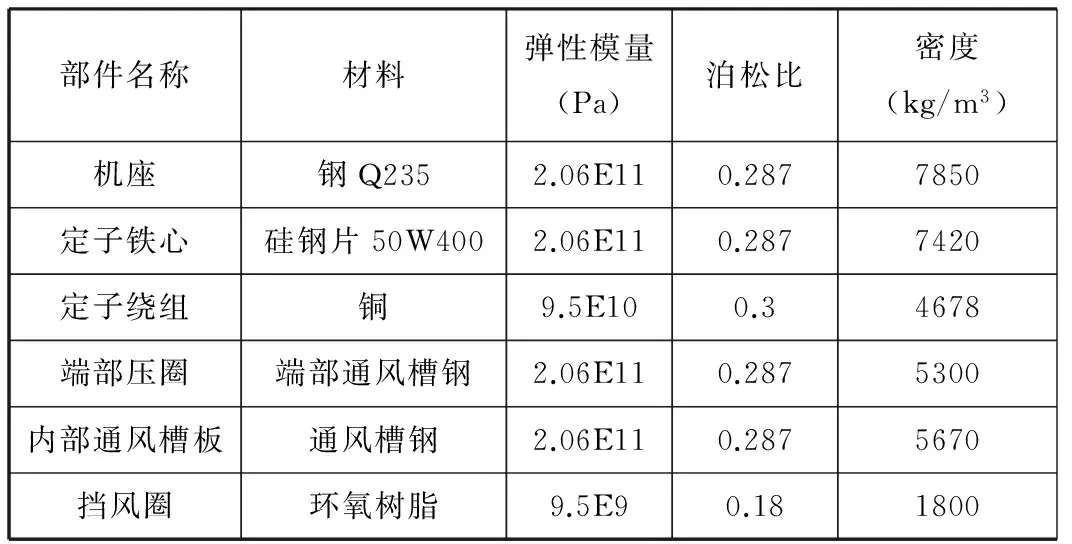
表3 定子系统零部件材料的力学属性Table3 Mechanical properties of parts and components of stator system

2) 结果分析

通过通用后处理模块POST1查看定子系统模态的分析结果，定子系统(无端盖)主要模态的固有频率如表4所示，部分模态固有振型如图5所示，其中n表示振动阶数，f表示频率。

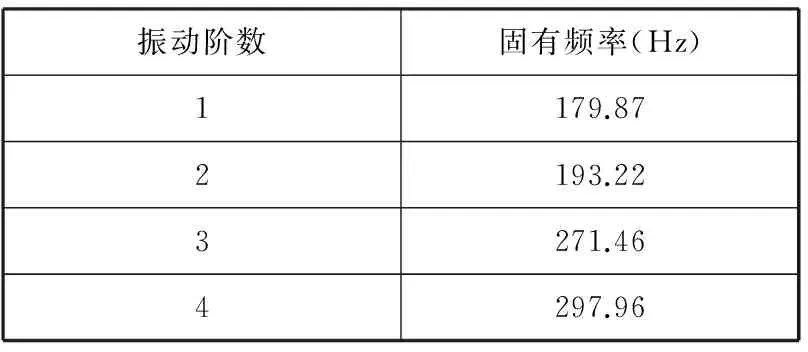
表4 定子系统(无端盖)主要模态的固有频率Table4 The natural frequency of the main mode of the stator system (without end cap)

(a) n=1，f=179.87Hz

(b) n=2，f=193.22Hz

(c) n=3，f=271.46Hz

(d) n=4，f=297.96Hz

4 定子模态测试实验

本次模态测试试验的原理图如图6所示：

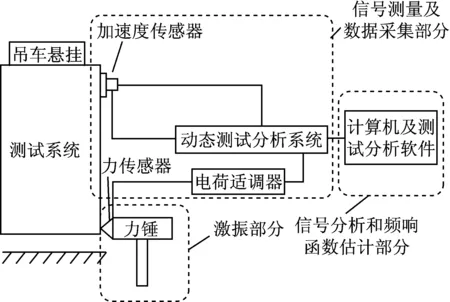
图6 试验原理图Fig.6 Schematic diagram of the test

根据原理图，对电机定子采用力锤单点锤击激振多点拾振的方法(SIMO)来测试并获得该电机所有模态参数。从图7可以看到电机定子的装配情况，绕组等定子零部件均已被安装在定子铁心上。

根据定子模态分析的结果(见表4)，本次试验关心的频率范围主要是160Hz到400Hz之间，经过参数识别，试验在频段范围内最终总共找到了四个明显的整体振型，见图8所示,其中n为振动阶数，f为固有频率，试验整体模态频率汇总见表5。

图7 电机定子(试验中)Fig.7 Motor stator(testing)

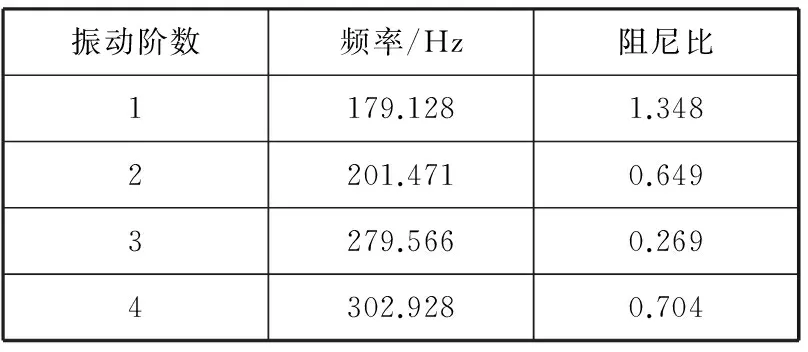
表5 150.156Hz～469.063Hz频段试验整体模态频率Table5 Modal frequency in 150.156Hz～469.063Hz frequency band

将试验结果视为真实值，则计算偏差等于计算模态频率减去试验结果的差除以试验结果，具体见表9。

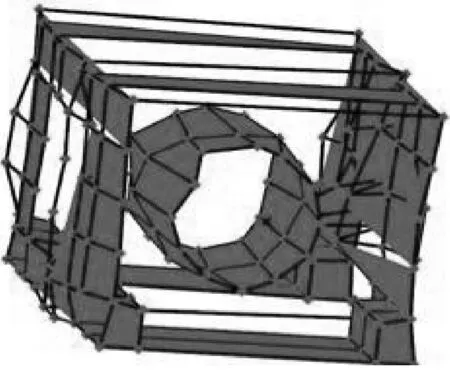
(a) n=1，f=179.128Hz

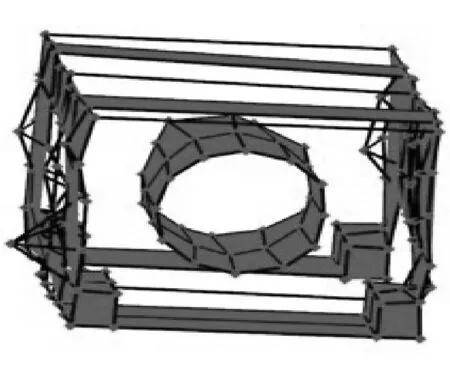
(b) n=2，f=201.471Hz

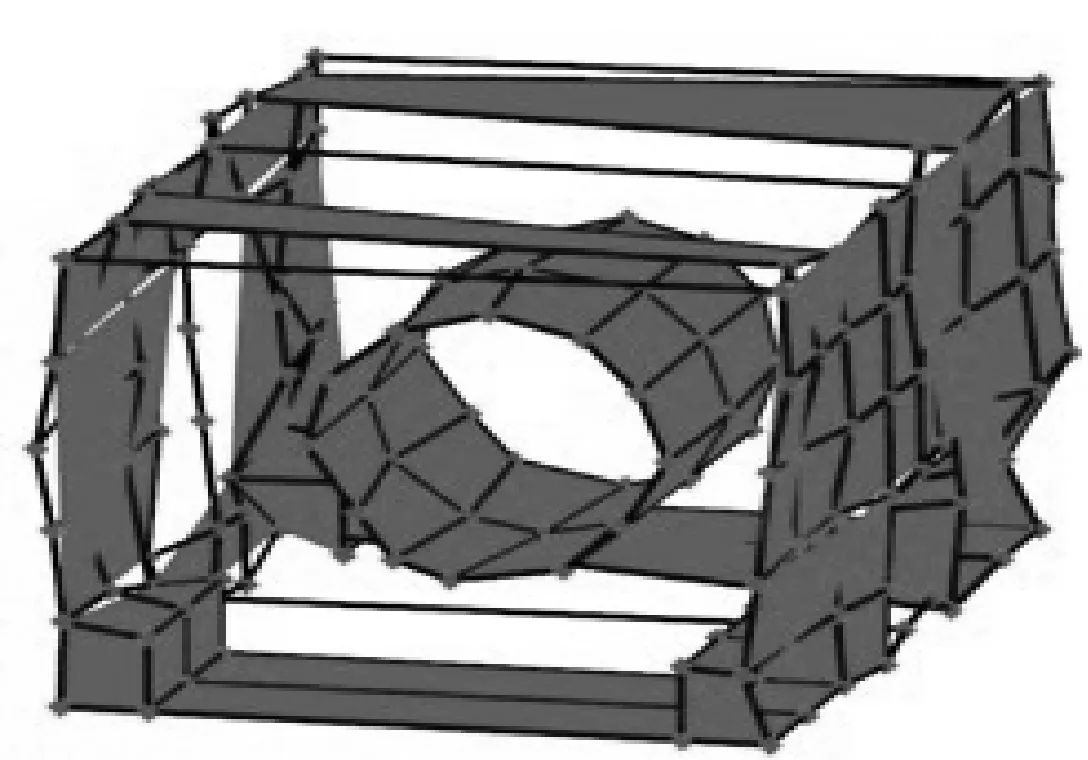
(c) n=3，f=279.566Hz

(d) n=4，f=302.928Hz

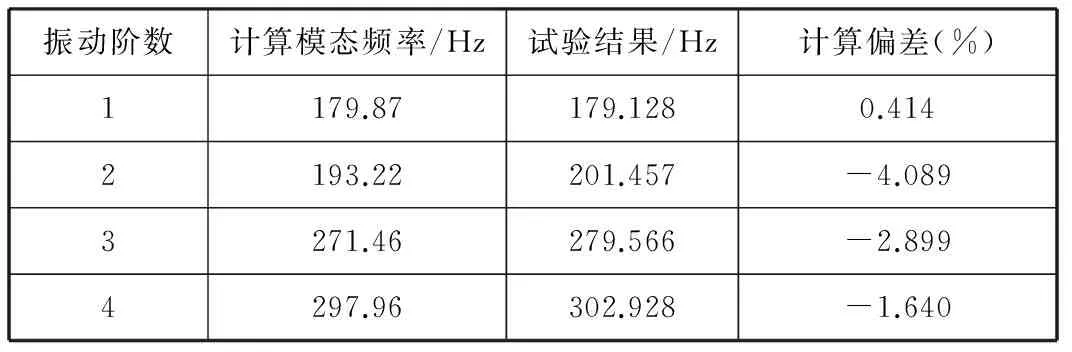
表6 定子系统计算模态频率与试验结果对比Table6 Comparison of modal frequency and test results of stator system

表9的频率值对比结果表明计算模态分析得到的前四阶整体振型与试验基本一致，而固有频率与试验相比偏差均不超过5%，达到了工程运用的精度。

5 结论

在模态分析原理的基础上，采用 Ansys软件对电机定子进行了模态分析。采用力锤单点锤击激振多点拾振的方法(SIMO) 对定子有限元分析结果进行了试验验证，试验结果与理论分析基本相符。这表明用有限元方法对异步电机做振动模态分析是一种有效方法，它能够为电机进一步的振动分析提供有价值的参考。

[1] 谢 颖,刘海松,刘海东,等.计及转子斜槽时笼型感应电机电磁振动变化规律的研究[J].中国电机工程学报，2015，35(15):40-42.

[2] 佟宁泽.大中型感应电机电磁力及定子振动分析[D].沈阳工业大学，2006.

[3] 王 玎,祝长生,符嘉靖.基于有限元的异步电机电磁振动分析[J].振动与冲击，2012，31(2):21-26.

[4] S.C.Chang，R.Yacamini.Experimental study of the vibrational behaviour of Machine stators[J].IEE Proc.-Electr.Power Appl., 1996, 143(3):242-250.

[5] GARVEY, S.: ‘The prediction of vibration in large electric machines’[D]. PhD thesis, University of Aston, 1998.

[6] Z.Tang，P.Pillay,，A.M.Li,C.Omekanda,C.Cetinkaya,Young’s Modulus for Laminated Machine Structures With Paticular Reference to Switched Reluctance Motor Vibrations[J]. IEEE Trans. Industry App.,2004,40(3):748-754.

[7] K.N.Srinivas，R.Arumugam.Static and Dynamic Vibration Analyses of Switched Reluctance Motors Including Bearings,Housing Rotor Dynamics,and Applied Loads[J]. IEEE Trans.Magn. 2004，40(4):1911-1919.

Modal Analysis of Induction Motor Stator

LiuDanzhong

(SchoolofMechanicalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240)

t Stator Modal analysis is an important step induction motor design. In this paper, using the finite element method to establish a model for YXKK710-6TH stator finite element model, and this stator modal analysis, the theory of the natural frequency of the stator, and the stator models were stator mode test results show that: the analysis results with experimental results was close. Related study concludes that the overall structural design and analysis of the vibration characteristics of the motor provides a useful reference.

Induction motor Stator Modal Analysis

1006-8244(2016)03-024-06

刘丹仲(1983-)，男，工程师，2011年至今为上海交通大学机械与动力工程学院工程硕士在读，现从事大型异步电机的设计及标准化管理工作。

TM343+.2

B