镜像多径引起的超低空目标跟踪指示角误差分析

肖 宇,郑桂妹,宫 健,郭艺夺

(空军工程大学防空反导学院,西安 710051)



镜像多径引起的超低空目标跟踪指示角误差分析

肖 宇,郑桂妹,宫 健,郭艺夺

(空军工程大学防空反导学院,西安 710051)

雷达导引头跟踪超低空目标时,由于目标镜像多径干扰会引起单脉冲跟踪指示角误差。文中建立了存在镜像目标时的单脉冲差和比模型,推导了单脉冲跟踪指示角误差模型,得到了开环与闭环跟踪模式的指示角解析表达式,仿真分析结果表明,对于开环跟踪,当镜像目标与真实目标相对相位相差180°时,指示角误差最大;对于闭环跟踪,指示角误差偏离程度与弹目距离、目标高度、天线增益、反射系数相关,弹目距离越近,指示角波动幅度越大。

镜像多径;超低空;目标跟踪;指示角误差

0 引言

防空导弹下视攻击超低空目标时,主动或半主动雷达导引头在开机后,进入自主寻的制导阶段,跟踪并拦截目标。在跟踪阶段,雷达导引头接收的回波信号中,多径干扰严重影响了雷达导引头的检测跟踪性能,文献[1-2]通过建立导弹飞行高度、弹目距离等目标特性参数的相互关系式,综合分析了多径效应对导引头截获/跟踪低空飞行目标的影响,文献[3-4]基于阵列天线结构,针对单脉冲测角提出了一种新的算法,或者通过结合传统多目标分辨算法和偏差补偿技术,有效削弱了多径误差对测角的影响,文献[5-6]主要对雷达导引头仰视目标时的仰角误差进行分析,文献[7]分析了当目标RCS不同时,多径、地海杂波等对雷达导引头目标检测具有不同的影响效果,上述研究主要是围绕抑制多径对角误差的影响以及多径对目标跟踪检测影响等方面开展工作,但对于雷达导引头在跟踪截获目标阶段,受低空多路径影响时,天线指示角是怎样变化的,变化程度如何还尚未有深入的研究。

文中针对雷达导引头下视拦截目标时,单脉冲天线指示角偏差问题,建立多径干扰时的指示角误差模型,并对其进行仿真分析,为下一步规避指示角误差提供参考。

1 单脉冲跟踪指示角模型

根据Sherman[8]关于点目标单脉冲响应的假设,在不考虑噪声和其他干扰源的情况下,当雷达导引头下视跟踪目标时,俯仰方向的单脉冲输出为:

d/s=kmε

(1)

式中:d/s为归一化差和电压信号比;ε为俯仰方位偏离导引头天线轴的偏轴角;km为与俯仰角相对应的单

脉冲响应曲线斜率,表示为伏特每波束宽度,其值通常约为1.6。

在防空导弹拦截目标时,雷达导引头天线扫描跟踪目标,在导引头的视线环境内,除了有真实目标运动的回波信号外,还有经由地海面反射产生的镜像目标回波,这个镜像目标相当于导引头角度分辨单元内的第2个目标。因而,根据式(1)可以推导出在镜像目标干扰情况下的偏轴角为:

(2)

式中:d和s表示差、和信号电压;ε表示偏离天线轴角度;下标t表示真实目标,下标i表示镜像目标;εti为合成指示角。从式(2)中可以看出合成指示角εti是真实目标离轴角度与镜像目标离轴角度的加权平均,由于真实目标与镜像目标不可分辨,此时雷达导引头产生了基于合成差和信号的单一指示角。

假设:

si/st=pejφ

(3)

对表达式(2)进行化简,得到

(4)

式(3)中p为镜像目标与真实目标回波信号的幅度比,φ为镜像目标与真实目标的相对相位。由于单脉冲处理器[9]在进行角度处理时,通常只提取指示角的实部信息进行处理,因而,经过单脉冲处理器进行处理的合成指示角εm可以表示为:

(5)

式中：Re表示取实部,这个指示角εm表示雷达导引头在跟踪目标时,由于镜像目标干扰导致天线偏离真实指向的角度。雷达导引头在跟踪目标时,有开环跟踪和闭环跟踪两种模式,当雷达导引头以开环模式跟踪真实目标时,也就是此时伺服环路并非闭环,其天线轴指向预先设定或预先计算的方向,此时开环系统的指向角εt、εi皆为固定值,对角εm进行变换可得:

(6)

此时指示角εm仅与镜像目标与真实目标的幅度比p和相对相位φ有关,假设p值固定,则可得指示角εm随相对相位φ的变化关系如图1所示。

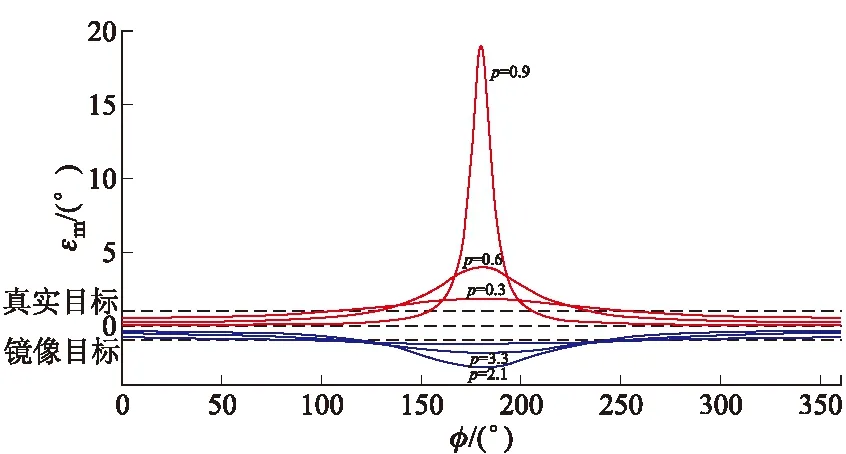
图1 指示角随相对相位变化趋势图

对式(6)进行分析,当p=1时,此时指示角εm为真实目标与镜像目标离轴角的中心点,表现在图1为一条直线,当p=0时,此时指示角εm为镜像目标的偏轴角εi,当p=∞时,此时指示角εm为真实目标的偏轴角εt,除此之外,对于特定的p值,指示角曲线则在真实目标与镜像目标之间进行波动,对于幅度p值介于0与1之间的偏轴指示角度εm趋向于真实目标,对于幅度p值介于1与∞之间的偏轴指示角度εm趋向于镜像目标。

从图1可以看出,对于任意的幅度p值,当镜像目标与真实目标相对相位增加时,指示角偏离天线轴的角度εm在不断增加,当相对相位达到180°时,指示角度εm达到最大,当相对相位再增加时,指示角度εm在不断减小,并且此时指示角度εm相对于相位180°呈对称关系,因而,为了使雷达导引头能够有效跟踪目标,在导弹攻击目标的飞行过程中,应当尽量通过改变目标飞行参数等措施,使得镜像目标与真实目标的相对相位远离180°的范围。

当雷达导引头处于开环跟踪模式时,由于天线轴固定,指示角仅与镜像目标和真实目标的幅度比p和相对相位φ有关,但是在实际自寻制导的导弹飞行过程中,指示角随着目标相对幅度和相位的变化而抖动,随着目标飞行高度、弹目距离的变化而变化,有时指示角在目标相对于雷达的角度范围之外,这种误差很大,以致引起跟踪丢失。

2 闭环跟踪指示角误差分析

当雷达导引头工作在闭环跟踪模式时,由弹目的相对位置提供粗略的角度信息,而使用指示角的偏差信息作为伺服系统校准的输入,控制天线轴向指向目标。此时对式(6)进行变换得到:

(7)

假设:

(8)

则式(7)表示为:

εm=εt+Δε

(9)

即指示角度εm为真实目标指示角εt与指示角误差Δε的求和,如果能够定量描述指示角误差Δε的变化,则能够描述出指示角度εm相对于真实目标指示角εt的波动范围,通过调整伺服系统,可以使指示角度εm趋向于0。

在镜像多径干扰情况下,雷达导引头下视跟踪超低空目标运动模型如图2所示。

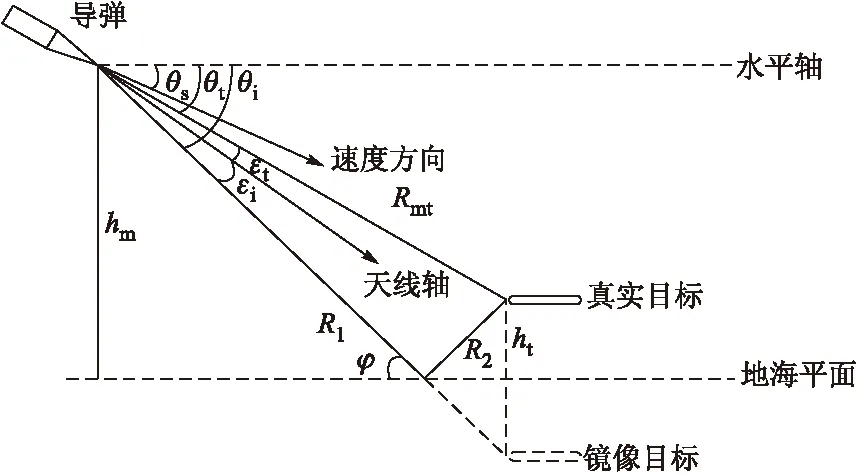
图2 多径条件下导引头弹目相对运动模型图

从图2中可以得出,导弹与目标之间的相关数学表达式为:

εt-εi=θi-θt

(10)

(11)

(12)

θi=φ

(13)

式中:θt为真实目标偏离水平轴的角度;θi为镜像目标偏离水平轴的角度;hm为导弹距离地海面的高度;ht为目标距离地海面的高度;Rmt为弹目距离;φ为导弹擦地角。根据弹目之间的关系可以得到镜像目标与真实目标的相对相位为:

φ=(R1+R2-Rmt)2π/λ+φ(φ)

(14)

式中:φ(φ)为反射系数的相位角。为了能够减小镜像多径干扰,文中雷达导引头探测信号采取垂直极化的方式,因而φ(φ)主要由垂直极化的反射系数决定。

式(11)、式(12)中的Rmt、hm、ht随着弹目距离和导弹制导方式的不同而不同,假设防空导弹采取修正比例导引法引导飞向目标,因而可以建立指示角误差Δε的计算流程如图3所示。

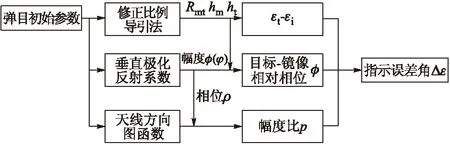
图3 指示误差角计算流程图

加载导弹与目标的初始参数,通过修正比例导引法求出目标运动过程中的弹目间距、离地高度,从而推导出导弹与真实目标和导弹与镜像目标视线之间的夹角,同时根据垂直极化反射系数的幅度和相位、天线方向图函数,求出真实目标与镜像目标的相对相位和幅度比,将这些计算参数代入式(8)中,即可得到指示角误差Δε的波动情况,整个指示角误差的计算流程如图3所示。

3 仿真及结果分析

当防空导弹拦截超低空飞行的目标时,导弹往往由地面发射至空中,然后下视攻击目标,假设在跟踪拦截段,弹目相距5 400 m,目标以300 m/s的速度贴地水平匀速飞行,导弹以700 m/s的速度向目标飞行,初始飞行高度为580 m,导弹以修正比例导引法向目标方向飞行,雷达导引头的工作波段为Ku波段,极化方式为垂直极化,波长为0.03 m,脉冲重复周期为0.2 s,从雷达导引头看向镜像目标与看向真实目标的RCS比值为1,分别对目标飞行至5 m、20 m、50 m的高度进行指示角误差仿真,结果如图4所示。

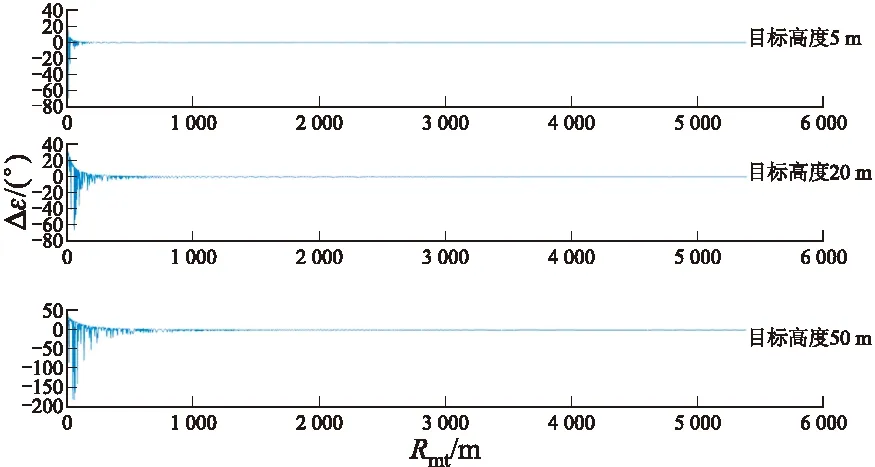
图4 指示角误差随弹目距离变化的趋势图

从图4可以看出,当弹目距离比较远时,无论目标高度如何,指示角误差趋近于0,此时指示角是真实目标的指示角,当弹目距离达到1 000 m时,指示角误差开始波动,弹目距离越近,波动越大,在弹目相距十几米时,波动最大,角度波动范围最大达到200°。在图4中,分别仿真了目标高度在5 m、20 m、50 m 3个高度的指示角误差,从图4中可知,当目标飞行高度越低,指示角误差较小,随着目标高度的增加,指示角误差越大,分析原因为当目标飞行高度很低时,真实目标与镜像目标相距很近,对于雷达导引头天线而言,此时二者偏离天线轴的角度都很小,而指示角误差是偏轴角的加权,因而,随着目标高度的增加,指示角误差在增大,当弹目距离越来越近时,对应的俯仰角变化率将发生剧烈变化,此时,无论坐标转换多么精确,由于伺服系统难以跟上目标方位变化率,极有可能发生目标失跟。

4 结论

雷达导引头在跟踪截获目标时,受低空飞行时多路径信号的影响,特别是受到镜像多径信号的影响,导致导引头可能出现失跟的现象,这种干扰直接导致导引头天线指向在弹目距离越近时发生剧烈的变化。文中根据单目标的单脉冲比,建立了导引头天线指示角误差模型,并对开环跟踪模式和闭环跟踪模式的指示角误差进行了仿真分析,对于开环跟踪,当镜像目标与真实目标相对相位相差180°时,指示角误差最大,对于闭环跟踪,指示角误差偏离程度与弹目距离、目标高度、天线增益、反射系数相关,弹目距离越近,指示角波动幅度越大,最终得出了影响天线指示角误差的弹目距离、弹目飞行高度、地海面反射系数的数学解析式,该式为下一步设计和规避多径影响的导引头相关参数提供参考和帮助。

[1] 曹原, 吴宁生, 高梅国, 等. 低空多路径下目标特性参数对PD导引头影响研究 [J]. 系统工程与电子学报, 2012, 34(2): 258-262.

[2] 张恒, 李青山, 张克舟, 等. 多路径效应下脉冲多普勒雷达导引头性能研究 [J]. 现代防御技术, 2014, 42(4): 92-97.

[3] PARK D, YANG E, AHN S, et al. Adaptive beamfor-ming for low-angle target tracking under multipath interference [J]. IEEE Transactiongs on Aerospace and Electronic Systems, 2014, 50(4): 2564-2577.

[4] 吕韶昱, 万建伟, 辛勤. 海面多径环境下雷达目标俯仰角测量提取的研究与应用 [J]. 国防科技大学学报, 2007, 29(5): 48-53.

[5] 党群, 吕善伟, 董胜波, 等. 雷达导引头跟踪低空目标仰角误差分析 [J]. 北京航空航天大学学报, 2004, 30(1): 36-39.

[6] 张瑜, 李竹兴. 雷达低仰角跟踪中的多径误差估算模型 [J]. 现代雷达, 1997(4): 16-21.

[7] 杨勇, 冯德军, 王雪松, 等. 低空雷达导引头海面目标检测性能分析 [J]. 电子与信息学报, 2011, 33(8): 1779-1785.

[8] SAMUAL M Sherman，DAVID K Barton. 单脉冲测向原理与技术 [M]. 周颖, 陈远征, 赵锋, 译. 2版. 北京: 国防工业出版社, 2013: 171-172.

[9] 高烽. 雷达导引头概论 [M]. 北京: 电子工业出版社, 2010: 99-102.

Analysis of Low-altitude Target Tracking Indication Angle Error Caused by Specular Multipath

XIAO Yu,ZHENG Guimei,GONG Jian,GUO Yiduo

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

When radar seeker tracks low altitude target, monopulse tracking indication angle error will be caused due to target specular multipath interference. To solve this problem, a difference and ratio model was established under specular multipath interference, a monopulse tracking indication angle error model was deduced, an indication angle analytical expression was derived when radar seeker worked in open-loop and closed-loop tracking mode. Simulation results show that, for open-loop tracking, when the relative phase difference is 180° between specular interference and real target, the indication angle error is maximum; For closed-loop tracking, indication angle error is associated with the distance between target and missile, target height, antenna gain, and reflection coefficient. The closer the distance between target and missile is, the greater the indication angle fluctuations.

specular multipath; low altitude; target tracking; indication angle error

2015-09-13

国家自然科学基金(61501504)资助

肖宇(1986-),男,福建将乐人,讲师,硕士,研究方向:防空反导武器系统总体。

TJ765

A