基于数据建模的空空导弹攻击区仿真

邓 健,王 星,曾艳丽,程嗣怡,张 炜

(1 空军工程大学航空航天工程学院,西安 710038;2 电子信息控制重点实验室,成都 610036)



基于数据建模的空空导弹攻击区仿真

邓 健1,2,王 星1,曾艳丽2,程嗣怡1,张 炜2

(1 空军工程大学航空航天工程学院,西安 710038;2 电子信息控制重点实验室,成都 610036)

为了分析某型空空导弹攻击区在多影响因素下的变化规律,提出了基于仿真数据建模的研究方法。使用四阶龙格—库塔法对攻击区快速模拟模型进行解算,计算结果存为数据库形式,并在此基础上对仿真数据进行二次建模分析。仿真结果具有良好的可视性,方便研究人员对其进行分析和利用,并且通过与现有结论进行对比,也证明了这种建模分析方法的科学可靠性。

空空导弹;多影响因素;攻击区;快速模拟;数据建模

0 引言

作为衡量空空导弹武器性能的重要标志,空空导弹攻击区一直以来都是业界研究焦点[1-12]。面向作战方案论证与战术运用分析的仿真需求对空空导弹攻击区模型提出了实时性甚至超实时性计算性能的要求。空空导弹攻击区建模,如何在复杂因素兼顾、精确建模和计算性能等多方面寻求一个折中平衡,成为目前作战应用仿真关注的问题之一。

针对以上情况,讨论了多影响因素下的导弹攻击区仿真,针对不同型号导弹特性,采用了空空导弹攻击区计算模拟数学模型,利用四阶龙格-库塔法求解积分计算,得到多个影响因素下的攻击区仿真数据,并将数据存储于本地数据库。在求得大量数据的基础上,利用Matlab对其进行分析,进行二次数据建模,提炼出与作战态势动态变化的规律,建立可直接运用于作战仿真的数据模型。这种数学建模与数据建模相结合的空空导弹攻击区域建模方法既兼顾多种影响因素,又能满足计算性能实时性甚至超实时性的运行要求。

1 需求分析

攻击区可以描述为载机高度Hf、发射速度Vf、导弹发射角φ、目标高度Ht、速度Vt、进入角q、双方机动状态、大气环境等因素的函数:

(1)

式(1)表明火控系统对攻击区进行建模解算是一项工作量巨大且复杂的工作,为实时显示发射时机,机载火控计算机必须依据交战双方空中的相对运动关系实时解算出导弹允许发射包线并及时将发射包线显示给飞行员,但由于受限于机载火控计算机的体积、运算速度和存储量,对导弹的攻击区需进行模拟逼近,特别是当火控计算机处理多目标信息时,需要根据不同目标态势进行各个攻击区的解算,并且往往需要付出降低攻击区精度的代价。

2 攻击区快速模拟建模

采取三自由度模型进行弹道解算的速度仍不能较好满足机载计算机的实时性与快速性要求[7]。文中模型采用快速模拟计算法进行空空导弹攻击区解算:将导弹与目标均视为严格按照理论轨迹飞行的二维模型,且载机、导弹、目标处于同一高度平面内,作用在导弹上的力简化为推力和气动阻力。导弹与目标间态势如图1所示。

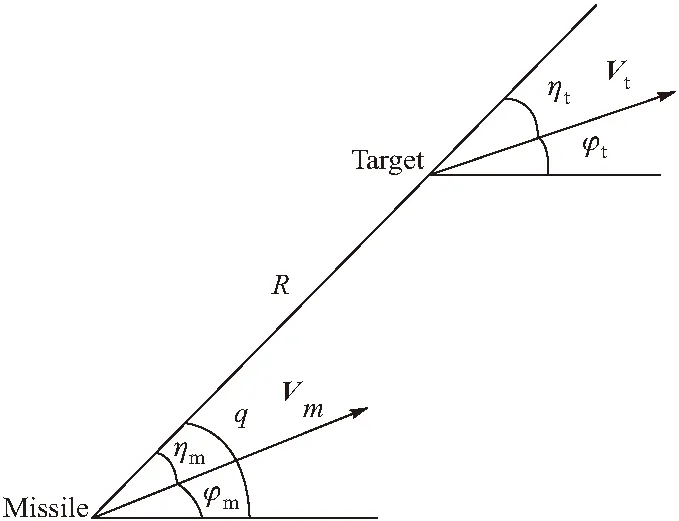
图1 弹目态势图

由导弹与目标相对运动关系可得:

(2)

式中:Vm为导弹速度;Vt为目标速度;R为弹目距离;q为目标进入角;q0为初始瞬时目标进入角;φm为导弹速度矢量与水平参考线间夹角;φt为目标速度矢量与水平参考线之间夹角,ε=0表示导引方程的通式,不同的导引方程对应不同的导引规律。

只考虑目标做1g过载匀速直线运动和4g过载匀速圆周运动:

(3)

式中C为常数。

末制导阶段,采用比例导引律,即:

(4)

式中：K为导引系数,取值一般为3～6[8]。

由导弹的受力模型,不考虑导弹的倾角,结合牛顿第二定律有:

(5)

式中:m为导弹质量;P为导弹推力;D为导弹所受阻力。

由于燃料的不断消耗,导弹质量随时间逐渐变小,导弹质量随时间变化模型描述为[9]:

(6)

式中:dm/dt为导弹质量变化率;ms为燃料质量秒消耗量,导弹在某一时刻的质量可以单独于导弹运动学方程之外求解[8]:

(7)

式中:m0为导弹初始质量;t0为发动机开始工作时间;tF为发动机停止工作时间。

综上,有简化的导弹弹道解算数学模型:

(8)

式中Vm,t为使用欧拉积分得出的t时刻的导弹速度。

通过对方程右侧使用四阶龙格-库塔法求积分,可以求出相应参数供机载火控系统进行导弹攻击区解算用,龙格-库塔法求积分公式如式(9)所示。

(9)

利用龙格-库塔法求积分过程为:

1)取初值x0,y0,h,n=1;

2)x1=x0+h,利用式(9)计算出y1,同时n=n+1;

3)令x0=x1,y0=y1,转回步骤2)计算x2,x3,…和y2,y3,…;

4)n>N,计算结束。

空空导弹攻击区的快速模拟解算流程如图2所示,图中,k为搜索算法的系数,k=0.5时为对分法,k=0.618时为黄金分割法[9]。

3 数据建模分析

以载机发射导弹高度固定为1 000 m时,最大允许发射距离随着各个参数的变化仿真为例。该条件下攻击区仿真结果如图3所示,图中蓝色线条是目标以1g过载机动时的最大允许发射距离变化曲线,绿色线条是目标以4g过载机动时的最大允许发射距离变化曲线。其中:(a)图为最大允许发射距离随目标进入角变化而变化的趋势图,(b)图为最大允许发射距离随目标高度变化而变化的趋势图,(c)图为最大允许发射距离随载机速度变化而变化的趋势图,(d)图为最大允许发射距离随目标速度变化而变化的趋势图。

图2 攻击区快速解算模拟

各影响条件的全排列可用矩阵理论中列向量与行向量相乘的思想来描述,设载机的速度取:Vc=[Vc1,Vc2,…,Vcn],目标的速度取Vt=[Vt1,Vt2,…,Vtm],全排列组合的数据组成一个n×m矩阵。

图中的坐标横轴值是特定某一因素的循环变化数值累加的结果体现。例如,图3(a)中,当进入角q离散取初值为A0=[0,10,20,30,…,180]时,第二段的取值此时变为A1=[180,190,200,210,…,360],照此循环累加下去,有:

(10)

这样便人为的将其他因素需要全排列组合分成了以q取值范围为“坐标段”的情况,从而可以较为方便的讨论其他影响因素全排列组合后得到的变化曲线,同理,载机在不同高度时的多因素条件下攻击区仿真也按照此方法进行。综上分析,可以有数据二次建模中循环取值描述模型:

n=1,2,…

(11)

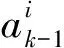
图3 多影响因素下空空导弹攻击区仿真

4 仿真结果分析

通过对仿真结果图3的分析可以得到:

1)多因素条件下,由于影响因素是按具有一定的“周期性”全排列组合的,导致空空导弹的攻击区变化趋势也出现了“周期性”变化规律,但具体来看其变化幅度值是不同的。这是因为当某一因素影响下虽然攻击区的变化趋势大致一致,但最大允许发射距离的数值发生了变化。

2)目标以1 g过载机动时其攻击区随着各因素的变化幅度大于目标以4 g过载机动时攻击区的变化幅度。这是因为目标逃逸时过载增大,攻击区的范围是减小的。

3)当图中蓝色与绿色线条重合时,可以认为是当前条件下,不论目标作何机动,我方均可进行攻击的“保险发射区域”。这是由于在允许发射距离计算时,目标做不同机动时,两种攻击区存在重合“区域”。

4)当目标进入角从的0°变为180°时,其最大允许发射距离增大。这是因为迎头攻击时,导弹与目标间的相对速度是两者之和;而尾后攻击时,则是两者之差,并且双方速度越大,其最大发射距离也相应变大,显然在同样时间内迎头比尾后飞行距离更远[10]。

5 结束语

文中在隐身空战条件下,通过对数学模型产生的仿真数据进行二次研究,在考虑多个影响因素的条件下进行空空导弹攻击区的仿真研究。得出的结论验证了这种基于数据建模分析方法的科学可靠性,这也为相关研究人员研究和使用空空导弹攻击区变化规律提供了一种新的研究手段。

[1] 张平, 方洋旺, 金冲, 等. 空空导弹攻击区实时解算的新方法 [J]. 弹道学报, 2010, 22(4): 11-14.

[2] 曲晓燕, 张林, 范庚. 基于Matlab/Simulink的空空导弹攻击区仿真 [J]. 弹箭与制导学报, 2011, 31(5): 51-54.

[3] 付书堂, 章惠君. 空空导弹攻击区高精度快速计算方法 [J]. 科学技术与工程, 2012, 12(27): 7074-7077.

[4] 柴世杰, 黄鹤松, 童中翔. 基于复合制导的中/远距空空导弹仿真 [J]. 计算机仿真, 2014, 31(12): 88-92.

[5] 吕超, 陈继祥, 辛旭光, 等. 超视距空战中空空导弹攻击效果模型与仿真 [J]. 兵工自动化, 2015, 34(3): 37-40.

[6] 顾佼佼, 刘卫华, 姜文志. 基于攻击区和杀伤概率的视距内空战态势评估 [J]. 系统工程与电子技术, 2015, 37(6): 1306-1312.

[7] 刘代军, 高晓光, 李言俊, 等. 中远程复合制导空空导弹允许攻击区计算 [J]. 航空兵器, 1998(2): 1-5.

[8] 雷虎民. 导弹制导与控制原理 [M]. 北京: 国防工业出版社, 2006: 49.

[9] 樊会涛. 空空导弹方案设计原理 [M]. 北京: 航空工业出版社, 2013: 57, 83.

[10] 丁琳. 多无人作战飞机协同攻击多目标的研究与应用 [D]. 西安: 西北工业大学, 2005: 53.

Simulation of Attack Area for Air-to-air Missile Based on Data Modeling

DENG Jian1,2,WANG Xing1,ZENG Yanli2,CHENG Siyi1,ZHANG Wei2

(1 Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China; 2 Science and Technology on Electronic Information Control Laboratory, Chengdu 610036, China)

In order to analyze overall change law of attack area of some certain air-to-air missile with multiple influencing factors, a new analytical method based on data modeling was proposed. Classical fourth-order Runge-Kutta was used to solve a fast mathematical simulation model, those calculation results were saved in database, and then a secondary model was build based on those calculation results. Visibility of the simulation result is good, compared with present conclusions, this analysis method is reliable.

air-to-air missile; multiple influence factors; attack area; fast algorithm; data modeling

2015-09-02

航空科学基金(20152096019)资助

邓健(1989-),男,山东聊城人,硕士研究生,研究方向:效能仿真,电子对抗理论与技术。

TJ762.2;TP391.9

A