高超声速飞行器仿真模型验证研究

马 震,吴晓燕

(空军工程大学防空反导学院,西安 710051)



高超声速飞行器仿真模型验证研究

马 震,吴晓燕

(空军工程大学防空反导学院,西安 710051)

针对高超声速飞行器仿真模型是否可信的问题,在对常用模型验证方法优缺点与适用范围分析的基础上,提出高超声速飞行器仿真模型验证方案。采用时、频域方法,对高超声速飞行器仿真模型进行验证,得出仿真模型的可信度。实验结果表明,采用时、频域分析方法,为高超声速飞行器仿真模型的可信度评估提供了一种较为有效的方法和途径。

高超声速飞行器;模型验证;时频域分析

0 引言

高超声速飞行器(hypersonic flight vehicle,HFV)通常指飞行速度大于5Ma的飞行器,具有非常重要的战略意义,以其独特的优势成为各国研究的重点。然而,由于HFV飞行非线性、强耦合和不确定性等因素,其仿真模型是否可信,能否正确反映原理模型的性能,是仿真界当前研究的热点和难点。国内外对HFV模型验证所做的研究不多,目前,从公开报道的文献得知,只有国内部分学者在这方面做了一些有意义的探索。北京大学的黄琳院士在文献[1]中分析了HFV对控制科学构成的挑战,同时也提到亟需一套有效的HFV建模与验证方法。天津大学的张希斌在文献[2]中提出了一种可行的HFV模型验证方案,将可信度等级较高的真实HFV模型作为参照,对真实模型的输出数据和简化模型的输出数据进行一致性比较,从而验证简化模型的有效性,另外张希斌在文献[3]中提出了基于小波变换的HFV模型验证方案,但并没有提出一套完整的HFV仿真模型验证方案。文中在已有研究的基础上,分析现有模型验证方法优缺点和适用性,对HFV仿真模型的验证进行了系统的研究。

1 高超声速飞行器巡航段仿真

针对高超声速飞行器仿真系统,以X-43A型飞行器为对象,进行巡航段飞行仿真实验,仿真系统主要涉及多个模块,各模块之间相互关联,包括:1)控制量输入模块;2)控制器模块;3)力和力矩计算模块;4)纵向运动模块。系统组成模块及关系如图1所示。

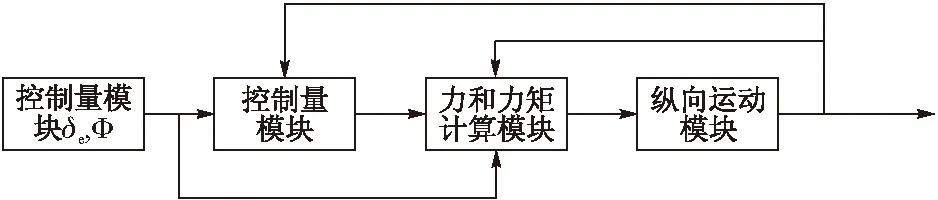
图1 HFV仿真系统组成模块及各模块间的关系

图1中,控制输入量为燃料/空气混合比Φ和升降舵偏角δe,仿真输出为5个刚体状态量(V,h,γ,α,Q)。仿真结果如图2所示。

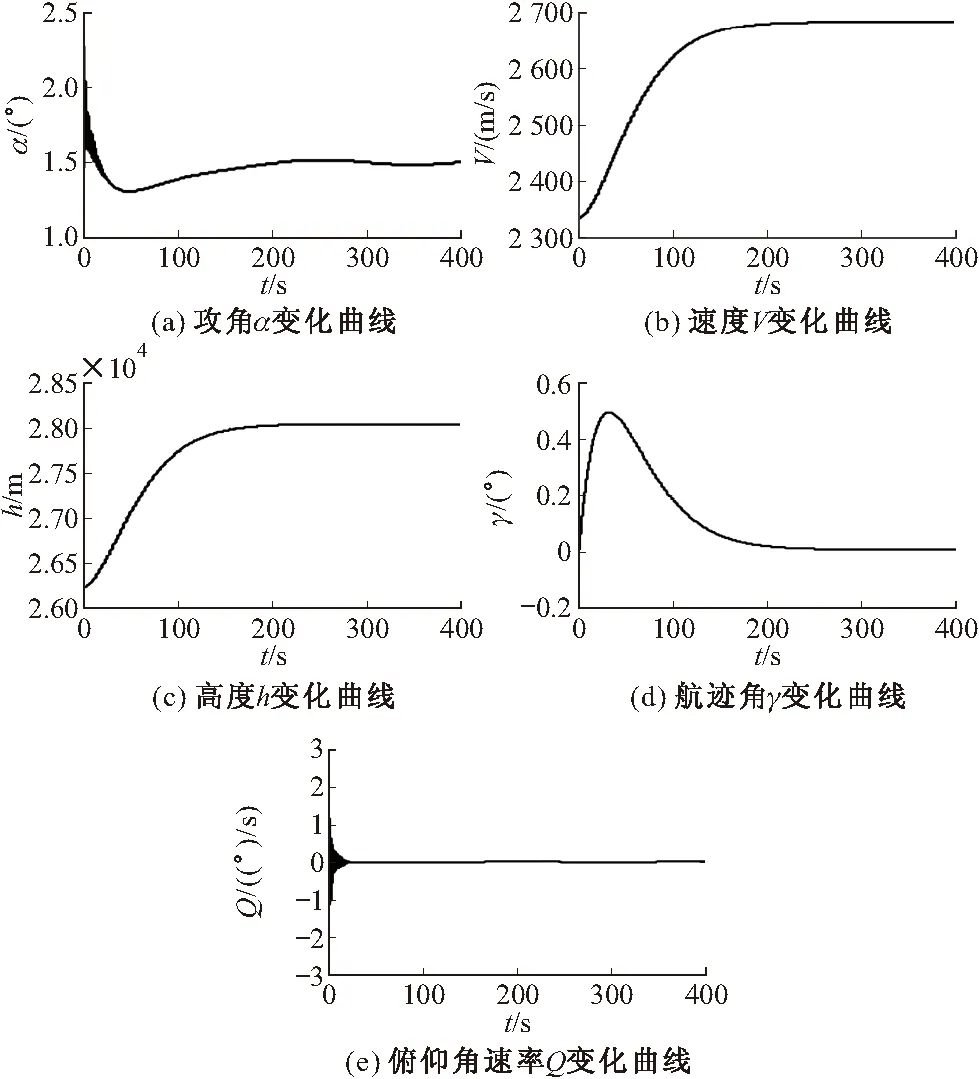
图2 HFV纵向运动数字仿真

由于受机身气动热载荷、超然冲压发动机工作条件等诸多因素限制,高超声速飞行器纵向平面具有一定的飞行范围,需满足飞行限制条件,即通常所说的飞行包线。根据文献[4-6]的报道,HFV纵向平面飞行包线如表1所示。

从图2(a)～图2(e)可以看出,各状态变量的仿真结果都在飞行包线参数容许的范围内变动,0～30 s攻角的变化比较剧烈,俯仰角速率与之相似;200 s之前属于爬升阶段,高度和速度随时间的变化基本一致,越来越大,之后上升到最高点,高度和速度维持不变,航迹角趋向于一个稳定的值。整个飞行过程中攻角都维持在1.5°左右,整个仿真效果比较理想。

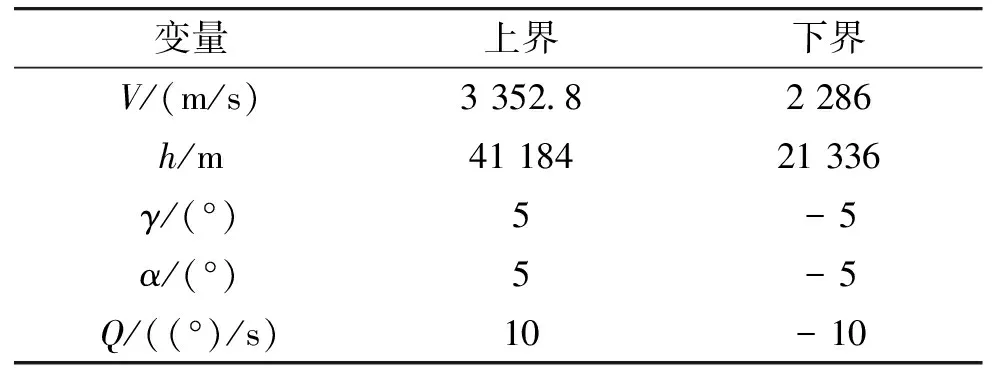
表1 HFV飞行包线参数范围

2 仿真模型验证方法

模型验证是从模型预期使用的角度出发,确定模型和有关数据代表真实世界正确程度的过程,传统的仿真模型动态验证方法一般分为时域方法和频域方法,其中时域方法一般不需要对原始时间序列进行复杂的变换和处理,且原理简单、实现方便,以TIC不等式系数法、灰色关联分析法等最具代表性。而频域方法则对动态响应时间序列有一些特殊需求,如平稳性等,一般需要对原始时间序列进行变换和处理,此类方法中比较有代表性的是谱估计法。两类方法都能从不同的角度实现对仿真模型的动态验证,是仿真模型验证领域常用方法。

模型验证方法按判断标准的不同划分,常用模型验证方法分类如表2所示。

表2 常用模型验证方法分类

3 HFV仿真模型验证

3.1 HFV仿真模型验证方案

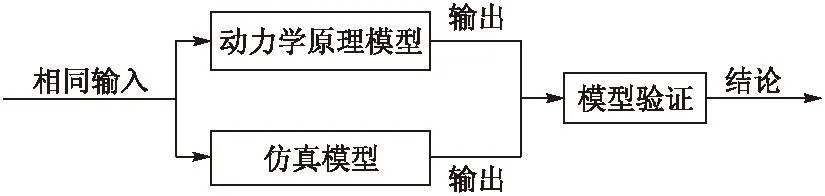
图3 HFV模型验证总体方案

针对高超声速飞行器仿真模型进行验证,验证的基本思想如图3所示,即将动力学原理模型作为参照,考察在相同输入条件下,仿真模型输出与原理模型输出的一致性程度,其中仿真模型的输出为待验证数据,称为仿真数据,动力学原理模型输出为参考数据。

HFV仿真模型共有5个输出,即高度h、速度V、攻角α、航迹角γ以及俯仰角速率Q。参照文献[2-3]对HFV仿真模型的验证方案,这里只研究攻角α的验证,其它4个状态的验证与之相似。

首先做初步的验证,可以绘制出攻角α随时间t的变化曲线,如图4所示。

图4 攻角α随时间的变化曲线

由图4可知,攻角α仿真数据和参考数据曲线基本一致,但这仅仅是一种主观定性的方法,不能给出置信水平,接下来应用时频域法进行验证。

3.2 基于时域法的HFV仿真模型验证

由于仿真数据和参考数据的分布未知,同时样本容量很大,不适合采用t检验和F检验进行仿真模型验证。因此,文中验证的思路为:首先选取均值、方差和标准差作为基本性能参数,检验两样本的基本性能参数是否一致,然后采用秩和检验法验证两样本概率分布的一致性。若两样本的均值、方差和标准差基本一致,又服从同一概率分布,则HFV仿真模型有效。

分别对仿真曲线和参考曲线进行采样,采样周期T=0.1 s,采样点为N=4 000,仿真数据序列和参考数据序列的均值、方差和标准差计算结果如表3所示。

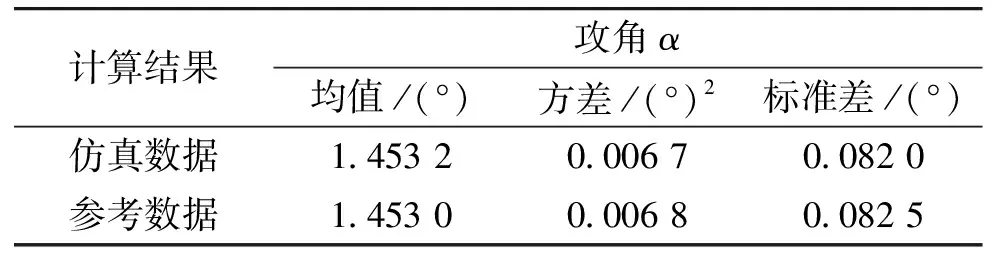
表3 攻角α均值、方差及标准差计算结果

由表3可以得出,仿真数据和参考数据的均值、方差和标准差几项性能指标相差无几,可以初步判断两组序列基本一致,接下来需要对其概率分布的一致性进行验证。

由秩和检验法对两样本概率分布的一致性进行检验,结果为两样本服从同一概率分布,验证通过。

通过数理统计法的验证,可以得出仿真数据与参考数据的均值、方差、标准差和概率分布具有很高的一致性,下面利用动态分析法验证仿真数据与参考数据在空间上的一致性。

1)TIC不等式系数法验证攻角α

①计算仿真数据和参考数据差值的平方和并开方

②分别计算仿真数据和参考数据的平方和并开方

③计算两组序列的TIC不等式系数

由计算结果可以看出,攻角α仿真数据与参考数据具有较好的一致性。

2)灰色关联分析法验证攻角α

①分别计算仿真数据和参考数据差值模的最小值及最大值

②取ξ⊂[0.1,0.5],计算两组序列的灰色关联度,如表4所示。

表4 不同分辨率对应的关联度

由表4可知,对于不同的分辨率要求,仿真数据与参考数据都具有较好的一致性。

3.3 基于频域法的HFV仿真模型验证

利用周期图法[7]对攻角α进行验证,首先对仿真数据和参考数据进行平稳化预处理,计算其傅里叶变换,再取其幅值的平方除以采样点作为时间序列的真实谱估计,周期图法的计算公式为:

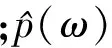
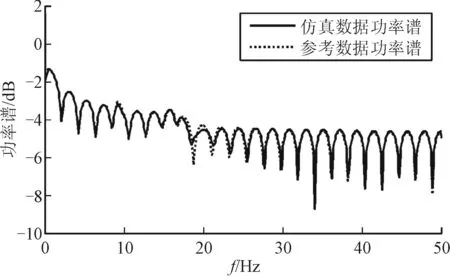
图5 攻角数据周期图谱估计

通过对攻角信号的谱分析可知,周期图谱估计法存在一定的缺陷,当数据长度较大时谱曲线起伏加剧。由图5可知,仿真数据和参考数据的谱估计曲线基本一致,可以初步判断仿真模型有效。但是通过谱图只能定性判断谱线具有相容性,带有一定的主观性,应进一步采用定量方法进行验证。

文献[8]中证明了假设成立的条件,即:

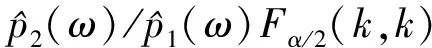
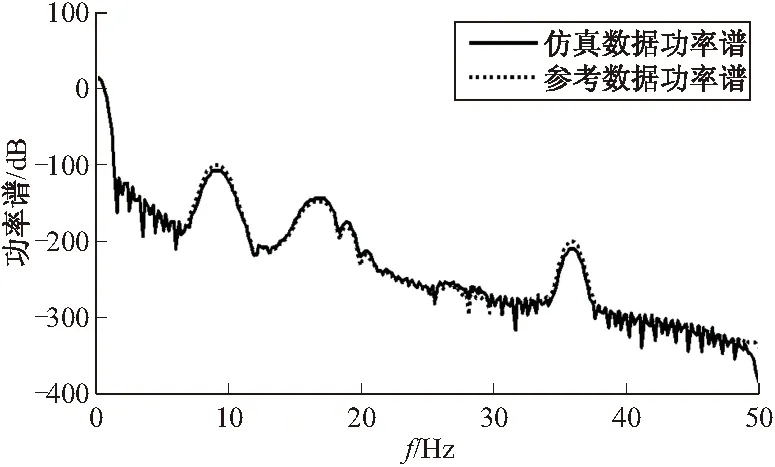
图6 攻角数据窗谱估计

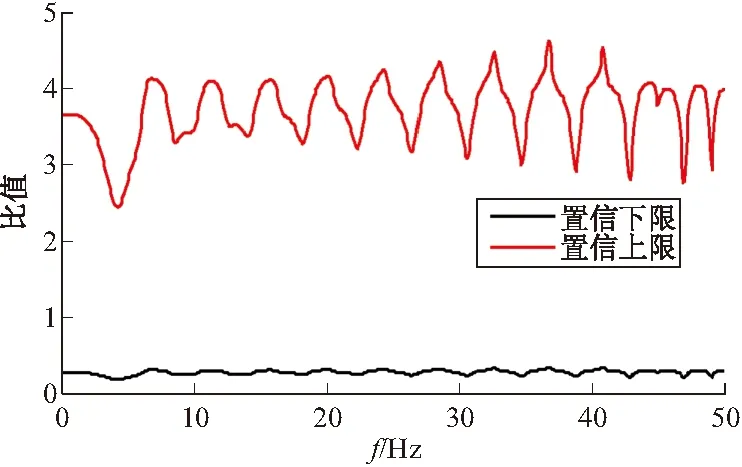
图7 置信带曲线

3.4 时频分析法的验证

从攻角输出时间序列可以看出,两组攻角数据都是非平稳信号,若采用傅里叶谱分析进行模型验证必须先对待验证数据进行预处理,从而造成原始信号局部信息的丢失。针对HFV仿真模型的特点,参考文献[9]中提到的导弹仿真验证的CLIMB方案,即等级高的数据其置信度也比较高,通过不同等级数据的比较分析,用高等级数据修正低等级数据,最终达到对导弹仿真模型验证的目的。

HFV原理模型输出数据(参考数据)属于高等级,仿真模型输出数据为低等级,选择窗函数为高斯窗,即η(t)=21/4e-πt2,这时STFT就变为比较常见的Gabor变换,由前面的分析可知,Gabor变换可以得到信号局部时间内的频域特性,因此采用Gabor变换对俯仰角速率进行验证,攻角的仿真数据和参考数据Gabor变换的幅值及时频分布分别如图8～图11所示。

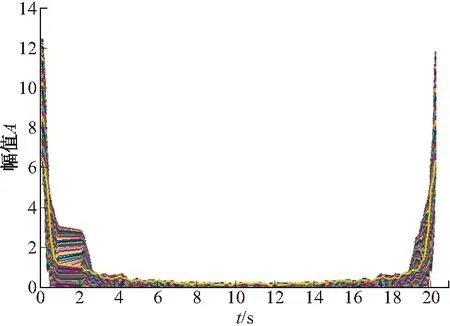
图8 仿真数据Gabor变换幅值

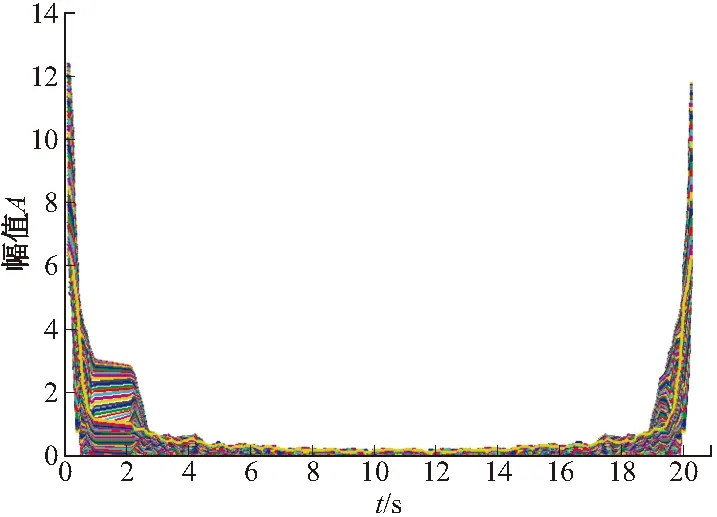
图9 参考数据Gabor变换幅值

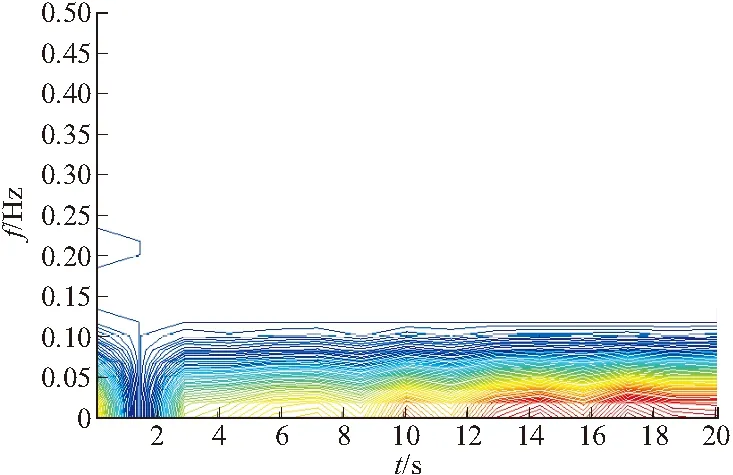
图10 仿真数据时频分布

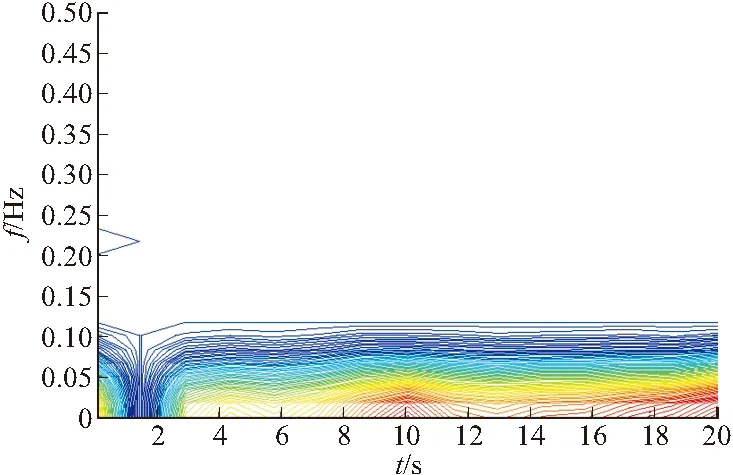
图11 参考数据时频分布

由图8～图11可以得知,仿真模型输出数据和参考数据的Gabor变换幅值的分布几乎一致,两组数据经过变换后在时频域的一致性也很好,这说明仿真模型具有较高的可信性。

4 小结

针对高超声速飞行器可信度问题,文中主要研究了HFV模型验证的时域法和频域法,各种方法都具有一定的通用性同时又各具特点。时域法中参数估计法一般要求大样本,样本还要服从某一分布,因此不能单独使用,应与其他方法综合起来验证仿真模型;动态分析法中,TIC不等式系数法对时间序列没有具体要求,且易于编程实现,使用简单,但只是一种定性验证,不能给出定量指标,灰色关联分析法只能判断两时间序列发展态势的一致性,不能判断其在空间上的举例,因此不能单独使用;谱分析法频域定位精确,分辨率高,但要求时间序列满足弱平稳条件,因此使用上受到了一定的限制;时频分析法同时兼顾了时域特征和频域特征,可以处理非平稳的时间序列,为HFV仿真模型验证提供了新的思路。

[1] 黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战 [J]. 控制理论与应用, 2011, 28(10): 1497-1505.

[2] ZHANG Xibin, ZONG Qun. Wavelet coherence analysis approach to model validation of the hypersonic vehicle model [C]∥Proceedings of the 32nd Chinese Control conference, 2013.

[3] ZHANG Xibin, ZONG Qun. Spectrum Analysis Approach to Model Validation of the Hypersonic Vehicle Model [C]∥2012 IEEE 6th Internation Conference on Information and Automation for Sustainablility, 2012: 71-75.

[4] 葛东明. 临近空间高超声速飞行器鲁棒变增益控制 [D]. 哈尔滨: 哈尔滨工业大学, 2011.

[5] WILLIAMS T, BOLENDER M A, DOMAN D B, et al. An aerothermal flexible mode analysis of hypersonic vehicle [C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit. Keystone, Colorado: AIAA, 2006: 1-22.

[6] PAKER J T, SERRANIA A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle [J]. Journal of Guidance, Control and Dynamics, 2007, 30(3): 856-869.

[7] 王凤瑛, 张丽丽. 功率谱估计及其Matlab仿真 [J]. 仿真技术, 2006, 22(11): 287-289.

[8] 李鹤, 吕岩, 杨明权. 基于频谱分析的飞行模拟器飞行性能验证 [J]. 军械工程学院学报, 2008, 20(6): 33-37.

[9] 符文星, 朱苏朋, 王建华, 等. 小波变换在导弹仿真模型验证中的应用研究 [J]. 弹箭与制导学报, 2006, 26(2): 174-176.

Research on HFV Simulation Model Validation

MA Zhen,WU Xiaoyan

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

To solve the problem of simulation credibility of the hypersonic flight vehicle (HFV) model, a way about HFV validation was researched based on characteristics and applicability of validation algorithms. The result of simulation credibility about HFV model was calculated through time and frequency domain analysis methods of validation. Example shows that the solution to the simulation credibility problem of HFV model is effective with time and frequency domain analysis methods.

hypersonic flight vehicle; model validation; time and frequency domain analysis

2015-07-11

陕西省自然科学基础研究计划资助

马震(1986-),男,陕西渭南人,硕士研究生,研究方向:建模与仿真。

TP391.9

A