一种改进的相关法自动拾取同相轴
◎刘兴利
一种改进的相关法自动拾取同相轴
◎刘兴利
基于各类同相轴自动拾取方法的优缺点,本文选择了能对噪声有一定压制作用并且容易实现的相关法作为基本方法,并对这种方法做了两点改进,建立模型数据,将普通的相关法和改进的相关法应用到模型数据中,对两者的拾取结果进行比较,并将改进的相关法应用到实际资料的同相轴自动拾取中,取得了较好的效果。
地震资料上各道振动相位的极值(波峰或波谷)的连线,就是同相轴。在对地震勘探资料进行解释时,常根据地震资料上成规律出现的,形状类似的振动来标出不同的同相轴,他们表示不同类别或不同层位的地震波。地震记录的同相轴拾取是一个既基础而又重要的问题,拾取结果的准确与否直接关系到后续的地震资料的处理。
目前为止,专家们已经提出了很多行之有效的自动拾取方法,可以分为四类。
第一类方法是根据地震资料的瞬时特征来拾取,如最大幅值法、能量比法及其改进方法等,基于瞬时特征的方法,主要缺点是受噪声影响大,如果地震资料信噪比较低,拾取结果准确度不高;
第二类方法是根据地震资料的整体特征来拾取,如相关法、约束初至法、线性最小平方预测法等,这些方法能压制一定的噪声,但受道间相关性影响,如果应用于地表情况复杂的地区,其拾取效果较差;
第三类方法是根据综合地震初至波多维信息的人工智能方法拾取,如人工神经网络法和分形法等,这些方法虽然拾取结果较为准确,但其原理步骤复杂,实现困难,且效率低;
第四类方法是根据数字图像处理原理的边缘检测法,此方法具有一定的抗噪能力,但要求同相轴起跳较为明显,如果地震资料所需拾取同相轴能量较弱,此法拾取效果不佳。
基于此,本文对常规的相关法做相应的改进,使其适用于信噪比较低,受干扰较强的地震资料的同相轴拾取。
互相关法拾取同相轴
互相关是衡量两道信号相似性的一种行之有效的数学方法。互相关的值是两道信号相对滑移距离的函数,相应每一滑移距离的互相关的值是由两组相应数据相乘值的和给出。互相关的值可正可负,其绝对值越大,说明两道信号在相应滑移距离位置数据的相似性越大,反之,相似程度越差。若两道信号的互相关值达到正最大,说明两道信号的相位相同;若两道信号的互相关值达到负最大,说明两道信号的相位相反。对于地震记录来说,各地震记录道的有效信号之间具有较好的相似性,这是相关法进行转换折射波旅行时间自动拾取的基本前提。
目前已经发展了很多种相关方法,这些方法的原理都一样,区别仅仅在于参考道的建立准则,常规的相关法有三种:选取一个固定的参考道,其他各道分别与参考道进行互相关,求取时移量。首先选取一个参考道,其相邻道与参考道进行互相关,计算完后,已经计算过的道作为参考道,再与它们各自的相邻道进行互相关,直到相关完整个记录,确定出每道相对时移。将共深度点或者共炮点道集内各记录道进行等时叠加,将其叠加结果作为参考道,再与其他各地震道进行互相关,求取时移量。
由于本文中改进的互相关自动拾取同相轴方法是基于第三种方法提出的,所以下面主要介绍这种方法的原理。
参考道的形成。首先,需要建立一个参考道,以参考道为标准,与各道进行互相关,这里是将共深度点道集内各记录道叠加的结果作为参考道(如图1)。设xj(t)表示每个地震道的振幅,j表示一个道集内各道的序号,叠加结果用y(t)表示,则有

图1 参考道的形成

此处N是道集内总道数,设k是振幅采样序号,K是振幅采样个数,将式(1-1)写成离散的形式为
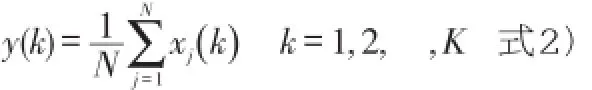
y(k)就是要求取的参考道。
用互相关方法求取相对位移。在一个选定的时窗内,使共深度点道集中各道和参考道进行互相关,求出相对时移。互相关公式如下:

T1、T2——时窗的起始和终了时间;
T2-T1——时窗长度。
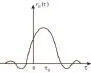
图2 相关函数曲线
按(式3)编制程序可以求取互相关函数曲线。图2就是上述互相关函数曲线的一个例子。相关函数曲线的极大值对应的τ值τk便是此道的相对时移量。对道集内的各道均用上述互相关方法求取τk。
同相轴拾取。首先,给定参考道标准时间,然后将每道与标准道进行相关,求出最大相关系数所对应的时移时间,参考道的标准时间加上相关最大值所对应的时移,即为该道的同相轴时间。
改进的相关法自动拾取同相轴
相关法对噪声有一定得压制作用,实现方法也简单,如果同相轴跳跃太大,拾取的结果就不准确,基于此,本文对常规的相关法作相应的改进,使其适用于各类同相轴自动拾取。
参考道的改进。与任何一个相关方法一样,首先需要建立一个参考道,以参考道为标准,与各道进行互相关。在参考道的形成中,本文对常规方法做了两点改进。一个关键的改进在于按照什么时间叠加形成参考道。常规方法一般是严格按照同样的时间进行叠加得到参考道。对于有些波,用一般的相关法完成旅行时间的拾取,是不可行的。此外,对于线性校正后,共炮点道集上各道旅行时间相差较大的波,简单的同一时间波形叠加会使各道静校正量互相抵消,使得参考道发生畸变(如图3),而导致相关后拾取旅行时间不准确。
图3 常规叠加参考道
本文所作的改进是首先根据理论计算或实际观测初步确定一个所需拾取同相轴可能的旅行时间范围,也即是后面所说的拾取时窗,然后在这个范围内求取幅值最大的峰值时间,最后以峰值时间为标准对各道的样值进行叠加就得到了参考道的样值,如图4。

图4 改进的参考道形成
本文对常规方法做的另一个改进是叠加形成的参考道要去掉本道的影响。因此,求取参考道的计算公式为:
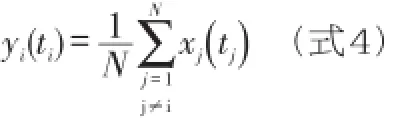
式4中,yi(ti)是求取的第i道的参考道,N是道集内总道数,tj=tj0±t是参与叠加的各道样值时间,tj0是参与叠加各道的峰值时间,ti=ti0±t是参考道样值时间,ti0是参考道基准时间,它可以是参考叠加各道的峰值时间的均值:
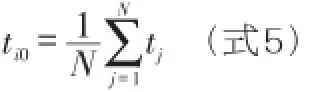
也可以是理论计算或实际观测给出的一个基准时间。
用互相关方法求取相对位移。此步骤与前述步骤相同,在此不复述。
旅行时间的自动确定。首先,利用理论计算或实际观测确定各参考道的基准时间;然后将各道与参考道进行互相关函数的计算,求出互相关函数中最大相关系数所对应的时移时间;参考道的基准时间加上相关最大值所对应的时移时间(有正有负),即为最后得到的该道的旅行时间。
几个重要参数。在拾取的过程中,还有几个关键参数设置问题需要注意:
相关时窗选取:时窗的大小,也即参考道,相关视窗一般以波组长度为宜,不过具体情况具体分析,如果同相轴起伏太大,就得加大时窗。
最大τ值的选取:τ值的选取根据地震记录的采样间隔Δt来确定的,将τ限定在(10-50)倍Δt,太大做互相关就容易导致串相位,太小又会影响拾取结果的准确度。
下面,通过测试数据来说明窗口参数的重要性。

图5同相轴剖面
图5是一个测试数据,图中能很清晰的看到两条同相轴1和2,同相轴1的能量明显的大于同相轴2的能量。为了便于比较,先自动拾取同相轴1。根据观察到的同相轴1的信息,设定视窗中间时间为600ms,视窗大小为100ms,得到的拾取结果如图6。可以看出,自动拾取出来的结果还是比较理想的。

图6 同相轴1自动拾取结果
接下来,对同相轴2进行自动拾取。根据观察到的同相轴2的信息,设定视窗中间时间为640ms,视窗大小为40ms,得到拾取结果如图7。可以看出,结果也是比较理想的。
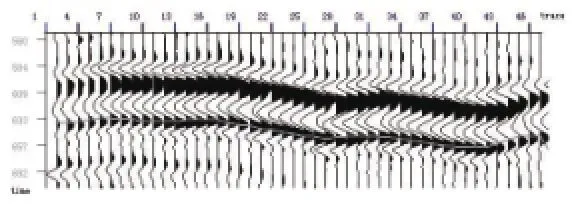
图7 同相轴2自动拾取结果
如果设定的视窗不正确,会出现什么样的效果呢?为此,在拾取同相轴2的时候,设定视窗中间时间仍为640ms,视窗大小改为60ms,这样的视窗拾取出来的结果如图8。可以看到,拾取结果发生了串相位,这是因为,设定的时窗过大,在拾取过程中,能量大的同相轴对能量小的同相轴会产生影响,如果拾取能量较强的同相轴就不会存在这一现象。所以,在拾取过程中,需反复修改时窗,以得到最为准确的旅行时间。
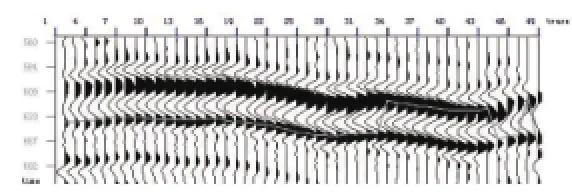
图8 错误时窗设置导致拾取串相位
模型数据自动拾取
根据模型数据,可以在炮集中很清晰的判断出所需拾取的同相轴的位置在时间140ms-160ms处,所以选择最适合时窗为中心时间145ms,时窗大小50ms。先用普通的相关法对同相轴进行了自动拾取,拾取结果如图9,选择同样的视窗,用改进的相关法对模型记录进行自动拾取,拾取结果如图10。

图9 常见的相关法拾取转换转换折射波

图10 改进的相关法自动拾取转换折射波
对比图9和图10,可以看出,图9的拾取结果比实际的同相轴偏上方,而图10中的结果和所需同相轴重合较好,这就说明了,本文对常见互相关法所做的改进,是有所成效的。
给模型数据加上噪声,然后再分别应用普通的和改进的相关法进行自动拾取,分析一下两种方法对噪声的抑制作用。普通相关法拾取结果如图11。图中,拾取的结果仍然是比较靠上,而在278道到284道中间拾取时间出现了塌陷,由于用的拾取时窗和前面未加噪声时的时窗是一致的,所以这个塌陷是由噪声引起的。再看图12,是用本文改进的相关法拾取的结果,在260道附近有几个明显的跳跃,除此之外,拾取还是比较成功,说明改进的相关法对噪声有一定的抑制作用。

图11 加入噪声过后的相关法拾取结果

图12 加入噪声过后的改进相关法拾取结果
实际数据自动拾取

图13 实际资料局部拾取结果
本文使用的实际数据是某油田工区的地震资料,经过仔细观察,选择最适合视窗为中心时间1250ms,视窗大小160ms,然后用改进的相关法对资料进行自动拾取,拾取结果如图13,在图中可以看到,在少数道处拾取结果有跳跃现象,除此之外,拾取结果比较准确。
结论及建议
相关法对噪声具有一定得压制作用,实现简单,但对同相轴的拾取结果较真实同相轴靠上;经过改进后的相关法,对噪声的压制作用较改进前效果更加明显,且拾取结果更为准确。在改进的相关法自动拾取同相轴的时候,关键的时窗参数要根据具体情况来设置,且需要经过反复的调节,才能得到满意的拾取结果。
(作者单位:贵州省煤田地质局)

