几何学概率的无线传感器网络能耗估计模型*

王昌征， 毛剑琳， 付丽霞， 郭 宁， 曲蔚贤

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)



几何学概率的无线传感器网络能耗估计模型*

王昌征， 毛剑琳， 付丽霞， 郭 宁， 曲蔚贤

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

针对无线传感器网络能耗这一问题，提出了一种基于几何学概率的能耗估计模型。以节点的状态转换为基础，建立了基于半Markov链的节点能耗模型，并引入概率分布函数的概念。从传感器节点随机分布出发，假定节点之间可以相互通信，分别对在单个正六边形和相邻两个正六边形内的节点随机分布进行研究，推导得出能耗估计模型。仿真结果表明:该模型可以实现网络能耗的准确估计。

无线传感器网络； 几何学概率； 半Markov链； 概率分布函数； 能耗估计模型

0 引 言

随着传感技术、通信技术和计算机技术的飞速发展，无线传感器网络(wireless sensor networks,WSNs)日益受到国内外的高度重视[1]。WSNs和传统的无线网络有着很大的区别，传感器节点体积较小[2]，自身装载的能源也比较有限。此外，大多数WSNs节点一旦布置好就不会轻易的移动，因此,传感器节点基本无法通过更换电池的形式来补充新的能源。大规模传感器节点的部署是大势所趋。因此，大规模传感器网络的能耗估计就显得越来越重要，但是大规模WSNs的能耗估计存在较大的难度。通过一种简易的方法对大规模传感器网络能耗进行估计，就显得尤为重要。

在以前的研究中，已经有大量关于能耗估计的研究。文献[3]提出了一种基于Markov链的休眠调度的能耗模型，文献[4]考虑节点的发送和接收状态建立能耗模型。文献[5]考虑节点状态的转换，提出了基于半Markov链的WSNs能耗模型。文献[6～9]通过研究表明，在正六边形的几何模型下对WSNs性能进行分析比在正方形和长方形的几何模型下研究更加接近真实的情况。本文通过正六边形几何模型作为研究区域的方法，考虑节点的状态，提出了一种能耗估计模型。模型的提出为大规模WSNs能耗的预测与估计提供了理论依据。

1 理论准备

文献[10]给出了节点距离分布的概率分布函数的定义，推导得出了在单个正六边形和相邻两个正六边形的几何模型下，节点距离分布的概率分布函数FD(d)和FTD(d)。

在WSNs通信的过程中，节点通信有一定的范围。为了分析方便，假设节点的通信方式为任意节点可以通信。通过Matlab 2012a，在边长L的单个正六边形和两个相邻正六边形中随机撒点，通过蒙特卡罗的方法模拟结果，得到节点距离概率分布的拟合函数，如表1所示。

表1 概率分布拟合函数

图1、图2为任意节点通信情况在单个正六边形和两个相邻正六边形模型下撒点10 000个的概率分布函数的仿真结果。仿真结果证明了理论的正确性，节点距离分布的概率分布函数与实际的节点分布情况近乎一致。

图1 单个正六边形概率分布函数Fig 1 Probability distribution function in single regular hexagon

图2 两个相邻正六边形概率分布函数Fig 2 Probability distribution function in twoadjacent regular hexagon

2 能耗估计模型

为了研究方便，本文对能耗问题的研究设定如下：考虑节点分布区域边界为单个正六边形和两个相邻的正六边形，节点通信方式为节点间相互通信。在此基础上根据半Markov链的节点能耗模型，引入上文提到的节点分布的概率分布函数。推导出能耗估计模型，对能耗进行估计。能耗估计模型的建立为估算大规模网络能耗提供了理论和现实依据。

2.1 基于半Markov链的节点能耗模型

在WSNs中，通信模块共有发送态(transmission status,T)、接收态(receiving status,R)、空闲态(free status,F)、睡眠态(sleeping status,S)4种不同的状态。4种状态下节点消耗能量是不同的。在一定的时间范围内节点的状态切换是随机的。这种概率的随机性，正好满足半Markov链的条件，因此本文引入半Markov链来建立节点的能耗模型。如图3所示，为节点的4种状态的转换图。通过该转换图，可以看出，4种状态相互转换的具体关系。这里规定P(i)为传感器节点在状态i下的概率。

图3 传感器节点状态转换图Fig 3 State transition diagram of sensor node

根据图3的状态转移的描述，可以用状态转移矩阵来描述这个转移的过程。设P为状态转移矩阵，得出WSNs中节点状态的转移矩阵P的表达式为

(1)

由于传感器节点在睡眠状态，不可能直接变为接收和发送状态，以此概率P(S|T)和P(S|R)为0。在转换时间t=nT内，传感器节点经历了n次转换，在n→∞时，无线传感器网络的状态转移概率为

(2)

式中P1,1,P2,2,P3,3,P4,4为节点在S态、T态、R态和F态4种状态下的稳态概率,且规定节点在这4种状态下消耗的能耗功率为PS，PT，PR和PF。那么可以求得在t=nT时间内的传感器节点能耗功率为

(3)

文献[11]指出，这4种状态的功耗比约为2 000∶400∶400∶1，所以,要降低网络的能耗，其关键就是使得尽可能多的节点处于睡眠状态。本文首先考虑节点处于发送信息状态(其余状态可依据比例求得)，且其数学模型选用文献[11]的网络通信能量模型

ET=(α+βdm)·L

(4)

式中ET为节点发送信息所需的能量；L为所发数据的长度；d为节点之间的通信距离；m为信号的消减因子；α为传输一比特信息所需的能量 (包括启动时消耗的能量)；β为传输过程中单位能量的损耗。

将式(4)两边同除以时间t，则有

PT=(α+βdm)·v

(5)

式中PT为能耗功率，J/s；v为数据传输速率，即无线信号比特率。式(5)中各参数值由具体的应用来确定，在简化分析时,可以取典型值。一般取值如下α=50 nJ/bit，β=0.001 3 pJ/bit/m4，m=4，v=10 kB/s。

又根据式(3)和式(5)，可以求得在t=nT时间内的传感器节点能耗功率为

P=t×(5×10-4P1,1PT+P2,2PT+0.2P3,3PT+0.2P4,4PT)

=t×(5×10-4P1,1+P2,2+0.2P3,3+0.2P4,4)×(α+

βdm)·v

(6)

2.2 能耗估计函数

节点的模拟能耗概率分布函数，以节点的距离为研究对象，得到一个能耗估计函数，以此来估计无线传感器网络的能耗。为了研究方便，定义如下：

定义1 能耗估计函数估计的能耗为：在节点都可以相互通信条件下，节点的总能耗。

定义2 节点距离的数学期望近似等于节点平均距离。

对概率分布函数FD(d)和FTD(d)求导可以得到概率密度函数fD(d)和fTD(d),则在单个正六边和两个相邻正六边形内随机播撒N个节点，节点距离的数学期望为

(7)

(8)

根据上述式(7)、式(8)，可以得到N个节点的所有分布距离和的近似公式，如式(9)和式(10)所示

≈N(N-1)×0.826 254 277 5L

(9)

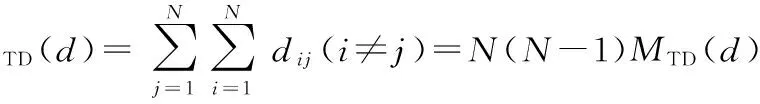
≈N(N-1)×1.858 336 696 6L

(10)

由此，可以推导出能耗估计函数得到函数的定义，如下：

定义4 设在单个正六边形或者两个相邻正六边形区域Ω中，随机撒点N个。任意节点可以相互通信，那么通过节点距离的期望来估计所有节点产生总能耗的函数为能耗估计函数，计算公式如下所示

P～D(d)=t×(5×10-4P1,1PT+P2,2PT+0.2P3,3PT+

0.2P4,4PT)

=t×(5×10-4P1,1+P2,2+0.2P3,3+0.2P4,4)×

(α+β(d～D(d))m)·v

(11)

P～TD(d)=t×(5×10-4P1,1PT+P2,2PT+0.2P3,3PT+

0.2P4,4PT)

=t×(5×10-4P1,1+P2,2+0.2P3,3+0.2P4,4)×

(α+β(d～TD(d))m)·v

(12)

式(11)为单个正六边形内能耗估计函数；式(12)为单个正六边形内能耗估计函数。上述公式可以快速、准确的估计无线传感器网络的总能耗。

这里通过仿真证明该模型的准确性，为此定义一个误差公式，如式(13)和式(14)所示，通过误差值的大小来证明能耗估计模型的准确性

(13)

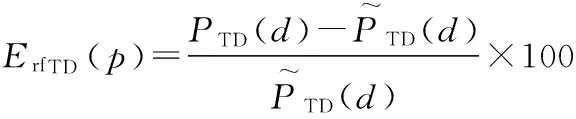
(14)

式中PD(d)为单个正六边形内实际总能耗，ErfD(p)为误差；PTD(d)为两个相邻正六边形内实际总能耗，ErfTD(p)为误差。

3 仿真验证与分析

3.1 仿真验证

假设各个传感器节点处于相互通信状态，在Matlab R2012a中，根据式(11)和式(12)，对能耗估计模型进行仿真，网络能耗仿真参数如表2所示。

在边长L=100 m的单个正六边形内和相邻两个正六边形内，在时间t=200 s，通过模特卡罗法对能耗估计函数对实际情况进行拟合，图4、图5为能耗估计函数以及拟合图。而且取节点个数N为3 000个，取t为200,400,600,800,1 000 s时，在边长L=100 m的单个正六边和两个相邻正六边形内，求出仿真的网络拟合总能耗、能耗估计值和误差值。进一步证明能耗估计模型的正确性，网络能耗对比如表3所示。

表2 网络能耗仿真参数

图4 单个正六边形能耗估计函数Fig 4 Energy consumption estimation function in singleregular hexagon

图5 两个相邻正六边形能耗估计函数Fig 5 Energy consumption estimation function in two adjacent regular hexagon

参数t=200st=400st=600st=800st=1000sPD(d)2.7864×10265.5743×10268.3602×10261.1151×10271.3942×1027P～D(d)2.7800×10265.5600×10268.3400×10261.1120×10271.3900×1027PTD(d)7.1117×10271.4224×10282.1336×10282.8448×10283.5560×1028P～TD(d)7.0844×10271.4169×10282.1253×10282.8338×10283.5422×1028ErfD(p)%0.2360.2570.2420.2790.300ErfTD(p)%0.3840.3850.3910.3880.389

3.2 仿真结果分析

从图4、图5的能耗估计函数的仿真图可以看出，除少数变化比较大的点以外，能耗估计模型非常接近拟合能耗函数，证明了能耗估计模型的准确性。从表3实际的参数值可以看出,能耗估计值与拟合值之间的误差小于1 %，这也进一步证明了能耗估计模型的准确性。由此，可以有效估计WSNs的总能耗。

4 结束语

本文在研究了单个正六边形和相邻两个正六边形内网络能耗与节点间距离的关系。本文先对Zhuang和Pan的距离分布函数的基础上利用蒙特卡洛法验证了节点距离概率分布函数的正确性，然后根据半Markov链的节点能耗模型，引入节点距离概率分布函数，推导出了能耗估计函数。然后利用Matlab 2012a仿真得出了估计能耗估计函数与拟合能耗的仿真图，给出了节点数N为3 000个，取t为200,400,600,800,1 000 s时，在边长L=100 m的单个正六边和两个相邻正六边形内，求出网络拟合的总能耗、能耗估计值和误差值,证明了能耗估计模型的有效性。该模型的提出为WSNs能耗的分析，为WSNs的节点配置提供了依据。在后继的工作中，将基于几何学概率进一步研究大规模WSNs的干扰和容量等问题。

[1] 谢和平,周海鹰,左德承，等.无线传感器网络能量优化与建模技术综述[J].计算机科学,2012,39(10):15-20,25.

[2] 陈 英,舒 坚,陈宇斌,等.无线传感器网络技术研究[J].传感器与微系统,2007,26(10):1-4，8.

[3] Shi Z S,Wang C F,Zheng P,et al.An energy consumption prediction model based on GSPN for wireless sensor networks[C]∥2012 the Fourth International Conference on Computational and Information Sciences,Chongqing,China:IEEE,2010:1001-1004.

[4] 王淑华,陈国定,赵国炳.一种无线传感器网络能耗模型及有效性分析[J].计算机应用与软件,2011,28(2):215-217.

[5] 魏 锐,蔺 莉.基于半马尔科夫链的无线网络能耗模型的研究[J].电子技术应用,2015,41(4):112-115.

[6] Zhuang Y,Pan J,Cai L.Minimizing energy consumption with probabilistic distance models in wireless sensor networks[C]∥The 29th IEEE International Conference on Computer Communications,San Diego,CA,USA:IEEE,2010:2453-2461.

[7] Zhuang Y,Luo Y,Pan J,et al.A geometric probability model for capacity analysis and interference estimation in wireless mobile cellular systems[C]∥The 54th Global Telecommunications Conference,Houston,USA:IEEE,2011:1-6.

[8] Baltzis K B.A geometric method for computing the nodal distance distribution in mobile networks[J].Progress in Electromagnetics Research,2011,114:159-175.

[9] Baltzis K B.Analytical and closed-form expressions for the distribution of path loss in hexagonal cellular networks[J].Wireless Personal Communications,2010,60(4):599-610.

[10] Zhuang Y,Pan J.A geometrical probability approach to location-critical network performance metrics[C]∥IEEE International Conference on Computer Communications,Munich,Germany:IEEE,2012:1817-1825.

[11] 胡风华.基于节点均匀分布的无线传感器网络能耗研究[D].淮南:安徽理工大学,2013.

毛剑琳，通讯作者，E—mail:km_mjl@aliyun.com。

Energy consumption estimation model for WSNs based on geometrical probability*

WANG Chang-zheng, MAO Jian-lin, FU Li-xa, GUO Ning, QU Wei-xian

(Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

Aiming at problem of energy consumption in wireless sensor networks(WSNs),propose an energy consumption estimation model based on geometric probability approach.This model establishes a model for node energy consumption based on semi-Markov chain on the basis of conversion of node state, and introduce the concept of probability distribution function.Start from random distribution of sensor nodes,assume that nodes can communicate with each other and research on random distribution of nodes in single regular hexagon and two adjacent hexagonals.Derive and obtain energy consumption estimation model.Simulation results shows that the proposed model can achieve accurate estimation of energy consumption of WSNs.

wireless sensor networks(WSNs); geometrical probability; semi-Markov chain; probability distribution function; energy consumption estimation model

10.13873/J.1000—9787(2016)12—0037—04

2016—02—24

国家自然科学基金资助项目(61163051); 云南省应用基础研究基金资助项目(2009ZC050M)

TP 393

A

1000—9787(2016)12—0037—04

王昌征(1990-)，男，山东青岛人，硕士研究生，主要研究方向为无线传感器网络覆盖。