用于航空发动机动态辨识的MSMEA-ELM算法*

许梦阳， 黄金泉,2， 潘慕绚

(1.南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，江苏 南京 210016；2.先进航空发动机协同创新中心，北京 100191)



用于航空发动机动态辨识的MSMEA-ELM算法*

许梦阳1， 黄金泉1,2， 潘慕绚1

(1.南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，江苏 南京 210016；2.先进航空发动机协同创新中心，北京 100191)

针对传统思维进化算法搜索半径缺乏目的性，临时子群体补充缺乏方向性以及神经网络训练速度慢、泛化能力不足，传统极端学习机隐含层神经元个数多的缺点，提出一种多群体自适应思维进化算法优化的极端学习机(MSMEA—ELM)算法，通过传感器数据训练该算法用于对航空发动机大范围动态过程进行辨识。以训练均方误差与权值2范数的加权和最小为优化目标，采用多群体自适应思维进化算法优化极端学习机。以某型涡扇发动机为研究对象，采用MSMEA—ELM算法进行航空发动机动态过程辨识，验证了该算法的有效性。

航空发动机; 传感器; 动态辨识; 思维进化算法; 极端学习机; 泛化能力

0 引 言

航空发动机模型通常包括动态模型和稳态模型，其中动态模型在航空发动机控制和故障诊断等方面有重要作用。基于智能算法进行航空发动机动态辨识具有重要的研究价值，文献[1,2]采用不同方法对航空发动机进行了动态辨识，但其研究的动态过程较小。文献[3]提出了训练速度快，泛化能力强的极端学习机，但其输入层到隐含层的权值及隐含层的阈值随机确定，且需要更多的隐含层神经元。文献[4]提出了基于差分进化算法的极端学习机，优化了网络结构和泛化能力。文献[5]分析了思维进化算法的收敛性，但算法尚存在搜索缺乏目的性等缺点。

本文针对思维进化算法趋同过程中散布半径缺乏目的性和异化过程中临时子群体补充缺乏方向性，提出一种多群体自适应思维进化算法优化的极端学习机(MSMEA-ELM)算法，优化过程以训练均方误差和权值2范数的加权和为适应度函数。以某型涡扇发动机为研究对象，取一组大动态数据作为训练样本，取慢车到最大状态的动态数据作为测试样本，进行动态过程辨识研究，以验证算法的有效性。

1 极端学习机

给定N个训练样本(xi,ti),i=1,2,…，N，其中，xi∈Rn为样本输入，ti∈Rm为样本输出，隐含层神经元个数为N～，激活函数为g(·)，回归模型为

(1)

式中wi=[wi1wi2…win]T为输入层到第i个隐含层神经元权值，bi为第i个隐含层的阈值，βi=[βi1βi2…βim]T为第i个隐含层神经元到输出层的权值。

写成矩阵形式为

Hβ=T

(2)

(3)

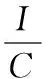
2 多群体自适应思维进化算法

2.1 自适应散布半径

针对散布半径固定，缺乏目的性的缺点，本文根据得分自适应确定散布半径，则第i个中心的散布半径

(4)

式中ci为第i个中心的得分，cmax为该子群体各中心的最高分，cmin为该子群体各中心的最低分，k和c0为常数，r为原固定的散布半径。

这样，得分高的中心散布半径较小，利于搜索到更优个体，得分较低的中心搜索半径较大，保证了搜索范围，搜索更具目的性。

2.2 第二临时子群体

思维进化算法在异化操作过程中，随机补充的临时子群体中心得分一般会远低于其它临时子群体得分，不利于异化操作对进化过程的推动；此外，初始群体利用率较低。因此，本文在群体初始化的过程中，将优胜子群体中心和临时子群体中心之外的个体设为第二临时子群体中心，并随之进行趋同操作，当临时子群体替代优胜子群体时，第二临时子群体按照得分由高到低依次补充优胜子群体。

3 MSMEA-ELM算法

3.1 适应度函数

在神经网络中，各层之间的权值越小，泛化能力越强[4,8]，为了同时优化训练精度和泛化能力，本文的适应度函数选取如下

(5)

式中C1,C2,C3为常数，E为训练误差，优化目标要使适应度函数达到最大。

3.2 MSMEA-ELM算法流程

2)选出其中得分最高的S1个个体和得分次高的S2个个体作为优胜子群体和临时子群体的中心，剩余个体作为第二临时子群体中心；

4)异化：当临时子群体得分高于优胜子群体时，用得分高的临时子群体替换得分低的优胜子群体，并用第二临时子群体中得分最高的群体补充临时子群体；

5)重复步骤(3)和步骤(4)中的操作直至进化完成或满足精度要求为止。

4 仿真算例

分别采用LM神经网络，ELM，MEA-ELM和MSMEA-ELM算法对如下SinC函数进行拟合，训练样本包含[-0.2，0.2]的噪声，测试样本不加噪声，仿真区间为[-10,10][3]，仿真结果如表1所示。

(6)

表1仿真结果表明：该算法具有训练速度快，泛化能力强，精度高等优点，可以满足拟合要求。图1给出了拟合结果，可以看出拟合精度高，满足要求。

图1 MSMEA-ELM算法Sinc函数拟合结果Fig 1 Fitting result of Sinc function based onMSMEA-ELM algorithm

5 航空发动机动态辨识

5.1 辨识原理

对于涡扇发动机，低压转子转速N1和高压转子转速N2是表征其工作状态的重要参数，本文以这两个参数为辨识目标，辨识结构如图2所示。

图2中每一个MSMEA-ELM相当于一个非线性映射，实际上就是

Ni(k+1)=fi(Wf(k+1),A8(k+1),N1(k),N2(k)),

i=1,2

(7)

式中f1,f2为非线性函数，N1,N2为低、高压转子转速，Wf为燃油量，A8为尾喷面积，k为仿真时刻。

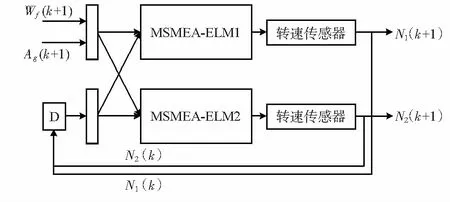
图2 航空发动机动态辨识结构Fig 2 Structure of aero-engine dynamic identification

5.2 仿真结果

以地面状态某动态过程的数据加上[-0.005,0.005]的噪声为训练样本，以其慢车到最大动态过程数据为测试样本。群体规模取100，优胜子群体规模取10，临时子群体规模取10，C1取1，C2取5×10-5，C3取5×10-5，k取1.2，c0取2，分别采用前述方法进行仿真，仿真结果如表2所示。

表2 航空发动机动态辨识仿真结果

图3给出了测试样本辨识输出和实际输出的仿真结果，通过图3和表2可以看出基于MSMEA-ELM算法进行航

图3 低、高压转子转速辨识仿真图Fig 3 Simulation diagram of low-pressure and high-pressure rotor speed identification

空发动机动态辨识具有较高的精度，N1的辨识精度在0.6 %以内，N2的辨识精度在1 %以内，保持了其变化趋势，满足精度要求，验证了MSMEA-ELM算法的优越性，其训练时间更短，泛化能力更强。

6 结束语

针对神经网络训练速度慢，泛化能力差及极端学习机隐层神经元个数多等缺点，提出一种多群体自适应思维进化算法优化的极端学习机算法，提高了训练速度，增强了泛化能力，通过非线性函数拟合验证了该方法的有效性。使用该方法进行航空发动机动态辨识，辨识精度高，在状态监测等方面有重要作用。

[1] 王海涛，谢寿生，武 卫,等.基于稀疏最小二乘支持向量机的航空发动机动态过程辨识[J].航空动力学报，2010，25(9)：2139-2147.

[2] 徐 亮，黄金泉.适用于全包线的航空发动机BP网络模型的动态辨识[J].南京航空航天大学学报，2001，33 (4)：334-337.[3]HuangGB,ZhuQY,SiewCK.Extremelearningmachine:Theoryandapplications[J].Neurocomputing,2006,70(1/3):489-501.

[4]ZhuQY,QinAK,SuganthanPN,etal.Evolutionaryextremelearningmachine[J].PatternRecognition,2005,38(10):1759-1763.

[5] 王川龙，孙承意.基于思维进化的MEBML算法的收敛性研究[J].计算机研究与发展，2000，37(7)：838-842.

[6]HuangGB,ZhouHM,DingXJ,etal.Extremelearningmachineforregressionandmulti-classclassification[J].IEEETransactionsonSystemsandCybernetics,2012,42(2):513-529.

[7]BartlettPL.Thesamplecomplexityofpatternclassificationwithneuralnetworks:Thesizeofweightsismoreimportantthanthesizeofthenetwork[J].IEEETransonInformTheory,1998,44(2):525-536.

[8]BoS.Optimalweightdecayinperceptron[C]∥ProcoftheInternationalConferenceonNeuralNetworks,1996:551-556.

潘慕绚，通讯作者，E—mail:pan_muxuan@163.com。

MSMEA-ELM algorithm applied in aero-engine dynamic identification*

XU Meng-yang1, HUANG Jin-quan1,2, PAN Mu-xuan1

(1.Jiangsu Province Key Laboratory of Aerospace Power System,College of Energy and Power Eengineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.Collaborative Innovation Center for Advanced Aero-engine,Beijing 100191,China)

In traditional mind evolutionary algorithm, the searching radius is lack in target and supplement of temporary groups is lack in direction,neural network had slow training speed and weak generation ability,traditional extreme learning machine has many nerve cells in hidden layer.In order to solve these problems,multi-group self-adaptive mind evolutionary algorithm optimized extreme learning machine(MSMEA—ELM)algorithm is proposed to solve these problems.Aiming at optimizing the adding of weighted mean square error and weighted 2 norm of weights,multi-group self-adaptive mind evolutionary algorithm is introduced to optimize ELM.The demonstration test is conducted on a turbofan engine and MSMEA—ELM algorithm is applied in aero-engine dynamic identification.The result shows that the introduced algorithm is efficient.

aero-engine; sensor; dynamic identification; mind evolutionary algorithm(MEA); extreme learning machine(ELM); generation ability

10.13873/J.1000—9787(2016)12—0129—03

2016—01—15

国家自然科学基金资助项目(51406084)；航空科学基金资助项目(2013ZB52030)；南京航空航天大学研究生创新基地(实验室)开放基金资助项目(KFJJ20150205)

V 233.7

A

1000—9787(2016)12—0129—03

许梦阳(1991-)，男，湖北襄阳人，硕士研究生，研究方向为航空发动机控制与故障诊断。