解决多元最值问题的八种有效策略

蔡勇全

(四川省资阳市外国语实验学校，641300)



○解题思路与方法○

解决多元最值问题的八种有效策略

蔡勇全

(四川省资阳市外国语实验学校，641300)

多元最值问题是指含有多个变量、以求解最大值或最小值为目的的一类数学问题.此类问题具有解答思维灵活、解法多样、涉及的知识面广、综合性强等特点,学生正确解答率普遍较低.本文结合实例介绍解决此类问题的八种有效策略,旨在探索题型规律,揭示解答方法,供大家参考.

一、判别式法

若目标函数通过一定的变形整理成为关于某一变量的一元二次方程,则可借助“实系数一元二次方程有实数解时其判别式非负”这一结论予以解决.

例1 若实数x,y满足log4(x+2y)+log4(x-2y)=1,则|x|-|y|的最小值是______.

解 由题设条件，可得

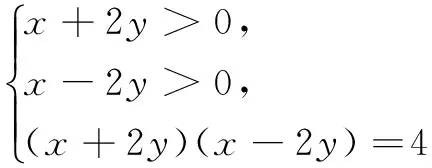
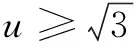
评注 在例1的解答过程中,将目标函数作为一个整体代换为元u,再变形整理为关于元u之外的其他元的一元二次方程,借助该方程有实根时判别式非负这一特点获解.

二、三角代换

求解多元最值问题时,若已知条件或已知条件变形后与某些同角三角函数关系式从形式上相似时,则可考虑用三角函数代替题目中的字母或式子,然后利用我们所熟知的三角公式进行化简.

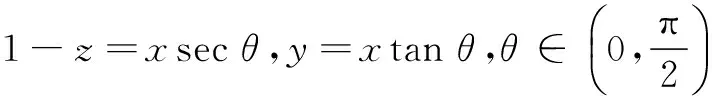
xy+2xz=x2tan θ+2x(1-xsec θ)

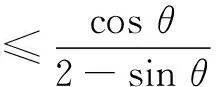
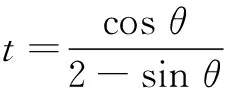
评注 由本题可见,三角函数的取值范围为探求多元最值问题提供了一种放缩视角.

三、待定系数法

待定系数法是指将目标多元代数式用条件中已有的多元代数式结合必要的待定系数表示出来,再按照一定的技巧求出待定系数,将问题转化为研究新表达式的相关指标

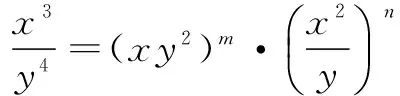
四、引入向量或复数

向量与复数是沟通代数和几何的重要桥梁,也是解决包括多元最值问题在内的众多数学问题的有效工具,巧妙运用向量与复数的性质可以使很多问题的解答“柳暗花明”.

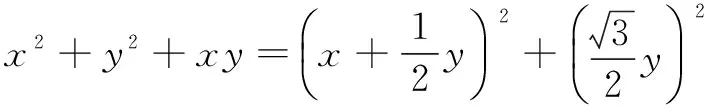
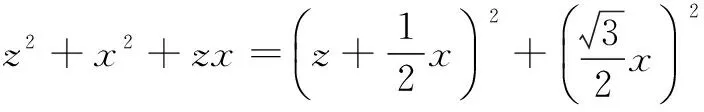
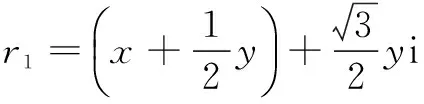
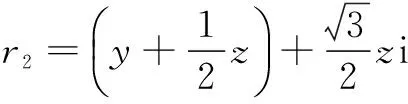
=|r1|+|r2|+|r3|≥|r1+r2+r3|

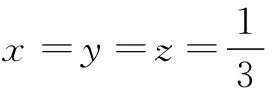
评注 构造复数或向量解答多元最值问题,简化了运算,有效降低了运算量,起到了事半功倍的解题效果.要常有构造意识,善于提炼出复数与向量这两种构造对象.

五、数形转化

华罗庚先生曾说过,“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事非”.可见,数形转化在处理数学问题时具有难以替代的优越性.事实上,对于多元最值问题,如果数形转化应用得当,往往能够化难为易,优化解题.

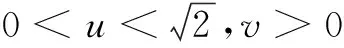
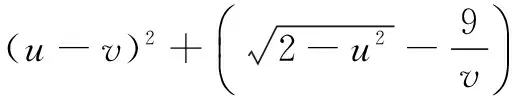
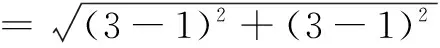
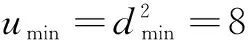
六、不等式法

这里的“不等式”主要是指基本不等式与柯西不等式,这些不等式关系及其等号的取得为求解多元最值问题创造了得天独厚的基础.

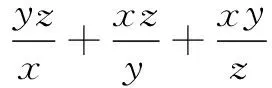
解 由基本不等式，得

≥x2+y2+z2,

≥3(x2+y2+z2)=3,

七、配方法

例7 设x,y∈R,求u=(y-1)2+(x+y-3)2+(2x+y-6)2的最小值.

解 由已知,

u=5x2+6xy+3y2-30x--20y+46

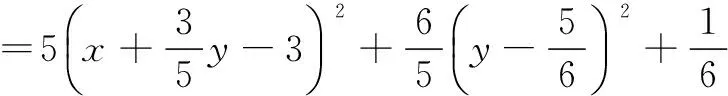
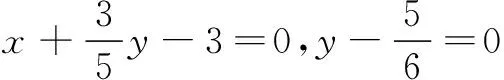
评注 利用配方法求解多元最值问题时,关键要注意两点：一是看是否能从目标函数中构造出条件式来；二是找出能够构造成完全平方的背景.

八、消(减)元归一

消(减)元归一是指通过不断的代入或实施加、减、乘、除运算,使题目中的多个变量逐渐消去或减少,直至最终只含有一个变量,然后利用函数知识获得最值.

例8 设实数x,y,z满足x+y+z=1,且x2+y2+z2=3,求xyz的最大值.

解 由已知消去变量z，可得

x2+xy+y2-x-y-1=0.

(*)

令x=a+b,y=a-b,代入(*)式整理，得

3a2+b2-2a-1=0.

所以由b2=-3a2+2a+1≥0，解得

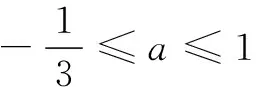
xyz=xy(1-x-y)

=(a+b)(a-b)[1-(a+b)-(a-b)]

=(a2-b2)(1-2a)

=(a2+3a2-2a-1)(1-2a)

=-8a3+8a2-1.

令f(a)=-8a3+8a2-1,得

f ′(a)=-24a2+16a.