一类二项式展开式问题的解法探究

黄 琼

(广东省阳江市阳西县第二中学，529800)



一类二项式展开式问题的解法探究

黄 琼

(广东省阳江市阳西县第二中学，529800)

一、问题的提出

2016年广州市一模给出如下一道试题：

问题1 在(x2-x-2)4的展开式中,x3的系数为______.(用数字填写答案)

分析1 为了能够使用二项式定理,因此可以考虑将x2-x-2分解因式,再用分类讨论.

解法1 由于(x2-x-2)4=(x+1)4(x-2)4,因此(x2-x-2)4的展开式中x3的系数应为(x+1)4的展开式中的x3的系数与(x-2)4的常数项的乘积,加上(x+1)4的展开式中的x2的系数与(x-2)4展开式中的x的系数的乘积,加上(x+1)4展开式中的x的系数与(x-2)4的展开式中的x2的系数的乘积,加上(x+1)4的展开式中的常数项与(x-2)4的展开式中的x3的系数的乘积的和，最后算出结果为-40.

评注 方法1通过分解因式,将一个陌生的问题转化为熟悉的二项式定理问题.但是,求解过程用到分类讨论,学生往往会漏掉或者算错某一种情况，最重要的一点是并不是每次遇到同类问题都能将括号的式子分解因式,这是方法1的缺点.

分析2 将x2-x-2=x2-(x+2)当作两个数x2、x+2的差,两次应用二项式定理,从而使问题得到解决.

评注 方法2用局部的整体思想将式子x2-x-2看作两项,应用二项式定理后,再对(x+2)4-k使用二项式定理,最后比较系数,从而使问题得以解决.

二、问题的拓展

上面我们用两种方法解决了一个括号内是三个数的二项式定理问题,但是它毕竟太特殊了.我们不妨考虑它的一般情形,并且试图从中得出一般结论类比二项式定理,我们可以提出以下一个问题:

问题2 对于给定的正整数n,求式子(x+y+z)n的展开式.

定理

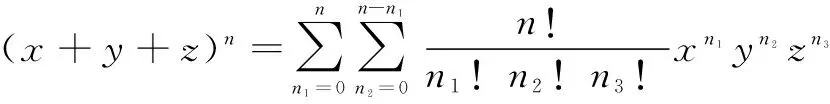
证明 由二项式定理，可得

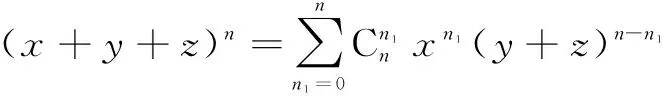
所以有

令n3=n-n1-n2,

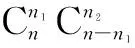
所以(x+y+z)n

证毕.

三、应用举例

例1 (2015年全国高考题)(x2+x+y)5的展开式中,x5y2的系数为( )

(A) 10 (B) 20

(C) 30 (D) 60

评注 上述定理将例1转化为解三元一次非负整数方程组的问题,而解方程从初中就开始学了,因此用此定理解决这类问题,学生比较容易上手,而且不易算错.

例2 在(x2-x+1)5的展开式中x3的系数为( )

(A)-30 (B)-24

(C)-20 (D)20

解 由上述定理可知(x2-x+1)5的展开式的通项公式为

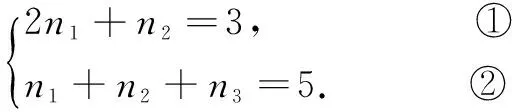
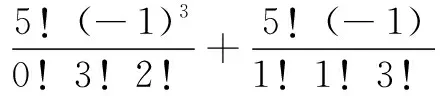
评注 从例2可以看出,上述定理无非是二项式定理的推广而已.由数学归纳法,我们还可以得到(x1+x2…+xk)n的展开式，这一点留给读者自己探讨.