一道高考数学试题的高等数学背景探究
关丽娜
(深圳大学书序与统计学院,518060)
一道高考数学试题的高等数学背景探究
关丽娜
(深圳大学书序与统计学院,518060)
一、问题重现
2016年上海高考理科数学试卷第10题:
设a>0,b>0,若方程关于x,y的方程组
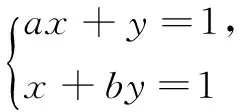
无解,则a+b的取值范围为______.
此问题的难点是已知条件“关于x,y的方程组无解”到底是什么意思?若能够把这个条件翻译出来,再把它转换为数学语言,从而得出关于a,b一个关系式,那么问题就不难解决了.然而,已知条件是一个关于二元一次方程组的解的存在性问题,它是线性代数中讨论的重点.那随意给出一个方程组,如何判断它有没有解呢?
二、对应的高等数学背景知识
关于x,y的方程组
①
称为二元一次线性方程组.
而方程组
②
称为方程组①的齐次线性方程组.
定义运算
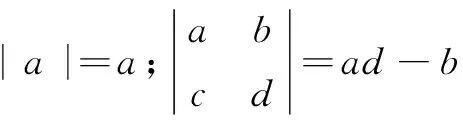
此运算分别称为1阶、2阶行列式.
根据高等代数的知识,方程组
有唯一解、无数解、无解的充要条件分别是
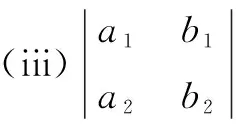
三、问题的解答
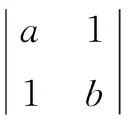
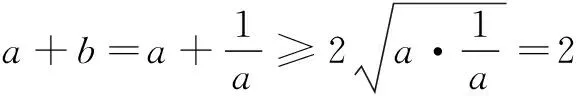
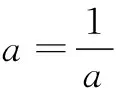
四、类比探究
上面的二元一次方程组有唯一解、无数解、无解的条件可以推广到n元一次方程组的情形中.这里面涉及到的内容非常丰富,希望有兴趣的学生或者读者自己去探索,这里我们指出一元一次方程的情形.
考查一元一次方程ax+b=0,那么它什么时候有唯一解、无数解、无解呢?我们类比二元一次方程组解的情形,将其进行探究.
首先将方程进行化简,可得ax=-b,则类比二元一次方程组的情形,当|a|≠0时,即a≠0时,方程ax+b=0有唯一解;当|a|=0且|-b|=0时,即a=b=0时,方程ax+b=0有无数解;当|a|=0且|-b|≠0时,方程ax+b=0无解,其中|a|表示一阶行列式.于是,由类比探究可得如下一个结论.
方程ax+b=0有唯一解、无数解、无解的充要条件分别是:
(i)a≠0;
(ii)a=b=0;
(iii)a=0,b≠0.
值得一提的是我们也可以依据上述结论去求解开头提到的高考题.过程如下:
(1-ab)x+b-1=0.
由已知条件,可得方程
(1-ab)x+b-1=0
无解.由上可得1-ab=0,且b-1≠0,即ab=1且b≠1.以下解法同上.
五、反思
每年高考都涌现出许多创新的试题,这些试题凝聚了命题者的智慧.对高考题进行课本题源的研究、竞赛背景探究、高等背景探究,无疑对提高教师的数学素养和培养学生的数学素养都有很大帮助.

