内悬浮外拉线抱杆风振响应研究

徐金城, 耿淑伟, 肖 峰, 周焕林

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.国家电网公司 交流建设分公司,北京 100052)



内悬浮外拉线抱杆风振响应研究

徐金城1, 耿淑伟1, 肖 峰2, 周焕林1

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.国家电网公司 交流建设分公司,北京 100052)

内悬浮外拉线抱杆作为一种特种起重设备,广泛应用于电力建设中。抱杆具有较大的长细比和特殊的约束形式,因此对结构进行风振响应分析是十分必要的。文章基于线性滤波法,利用Matlab模拟脉动风荷载,施加于ANSYS建立的抱杆模型上,对抱杆进行风振响应分析。通过分析,揭示了抱杆的风振特性,给出其在工作状态下的风振系数,为抱杆的设计和使用提供参考。

内悬浮外拉线抱杆;线性滤波法;风振响应;风振系数

0 引 言

随着我国特高压电力建设的日益发展,国家电网对特高压的投资建设也越来越大。内悬浮外拉线抱杆作为一种特种起重设备,其成本与其他起重设备相比低廉且组装方便,因此在输电线路的施工过程中,采用其分解组立输电塔成为一种常用的方法。

国家电网在浙北—福州1 000 kV输电线路铁塔的建设过程中,17个标段组塔方案中的多数标段都采用了内悬浮外拉线抱杆进行组塔。由于内悬浮外拉线抱杆在工程中的大量使用,它在施工过程中的安全性日益引起人们的重视。抱杆由于其较大的长细比和特殊的约束形式,在高空中作业与高层建筑一样,风荷载是其主要的动力荷载,在静力分析的基础上需要针对结构进行必要的风振响应分析,以保证其在施工过程中的安全,从而保障施工人员的人身安全,避免不必要的经济损失,保障电力建设安全、有序进行。然而,目前关于抱杆的风振响应分析较少,因此针对内悬浮外拉线抱杆进行风振响应分析是十分必要的。

本文以安徽送变电工程公司自行设计、制造的内悬浮外拉线抱杆(以下简称“抱杆”)为例,采用线性滤波法模拟各节点脉动风荷载时程[1],以节点荷载方式施加于有限元模型[2],对抱杆进行风振响应分析,为其设计和使用提供一定的参考。

1 抱杆模型介绍

抱杆模型采用ANSYS有限元软件建立,主材、斜材、腹杆采用BEAM188单元(三维线性梁单元),承托绳、外拉线采用LINK10单元(3D仅受拉杆单元),抱杆端部加强板采用SHELL63单元(弹性壳单元),有限元模型如图3所示。其中,单元2401至2404为承托绳,单元2405至2408为外拉线,图中箭头表示在吊重作用下,抱杆顶端沿各方向上的分力。

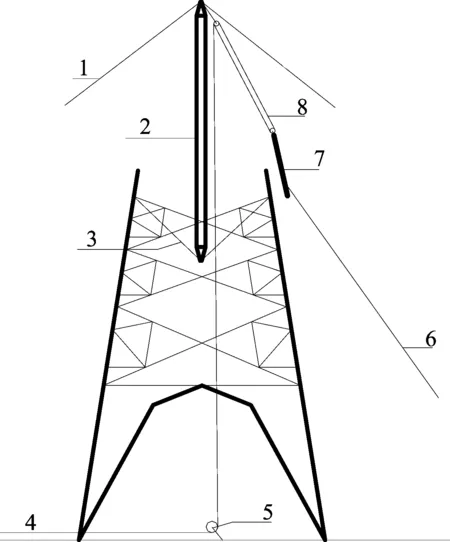
1.外拉线 2.抱杆 3.承托绳 4.牵引绳 5.地滑车 6.控制绳 7.吊件 8.起吊滑车组

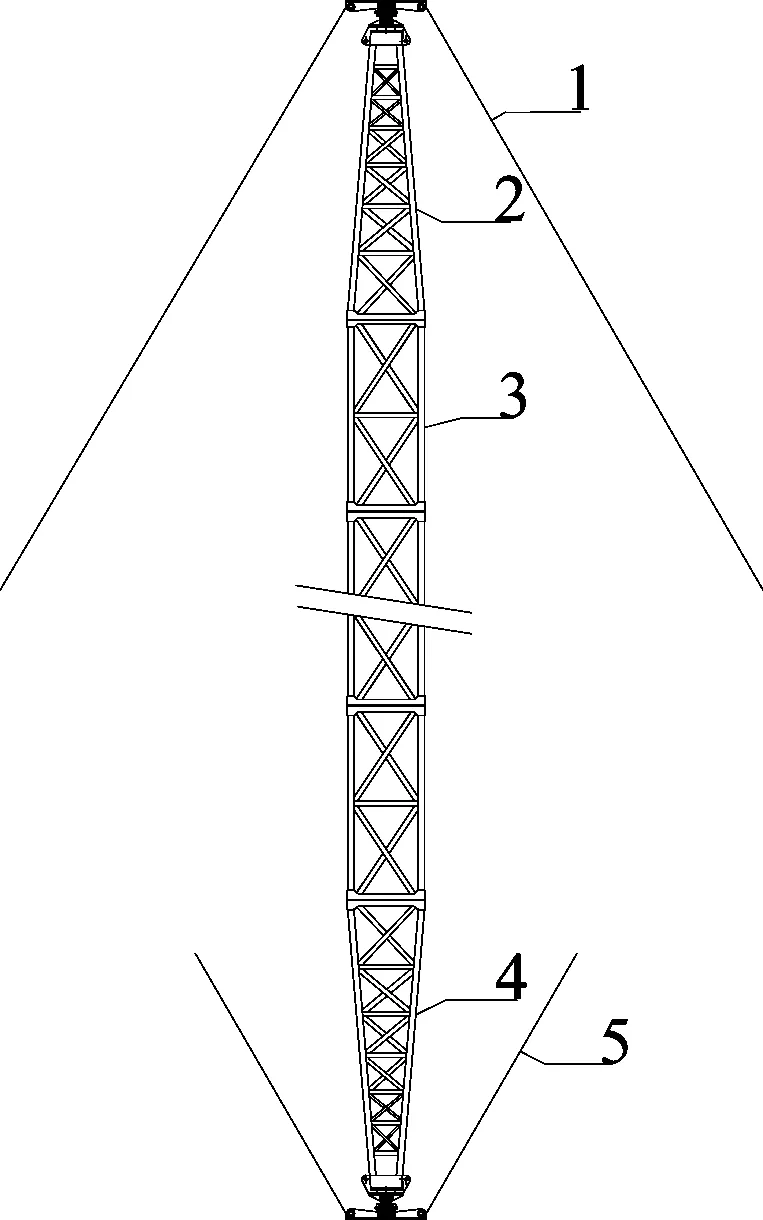
1.外拉线 2.上锥段 3.标准节 4.下锥段 5.承托绳

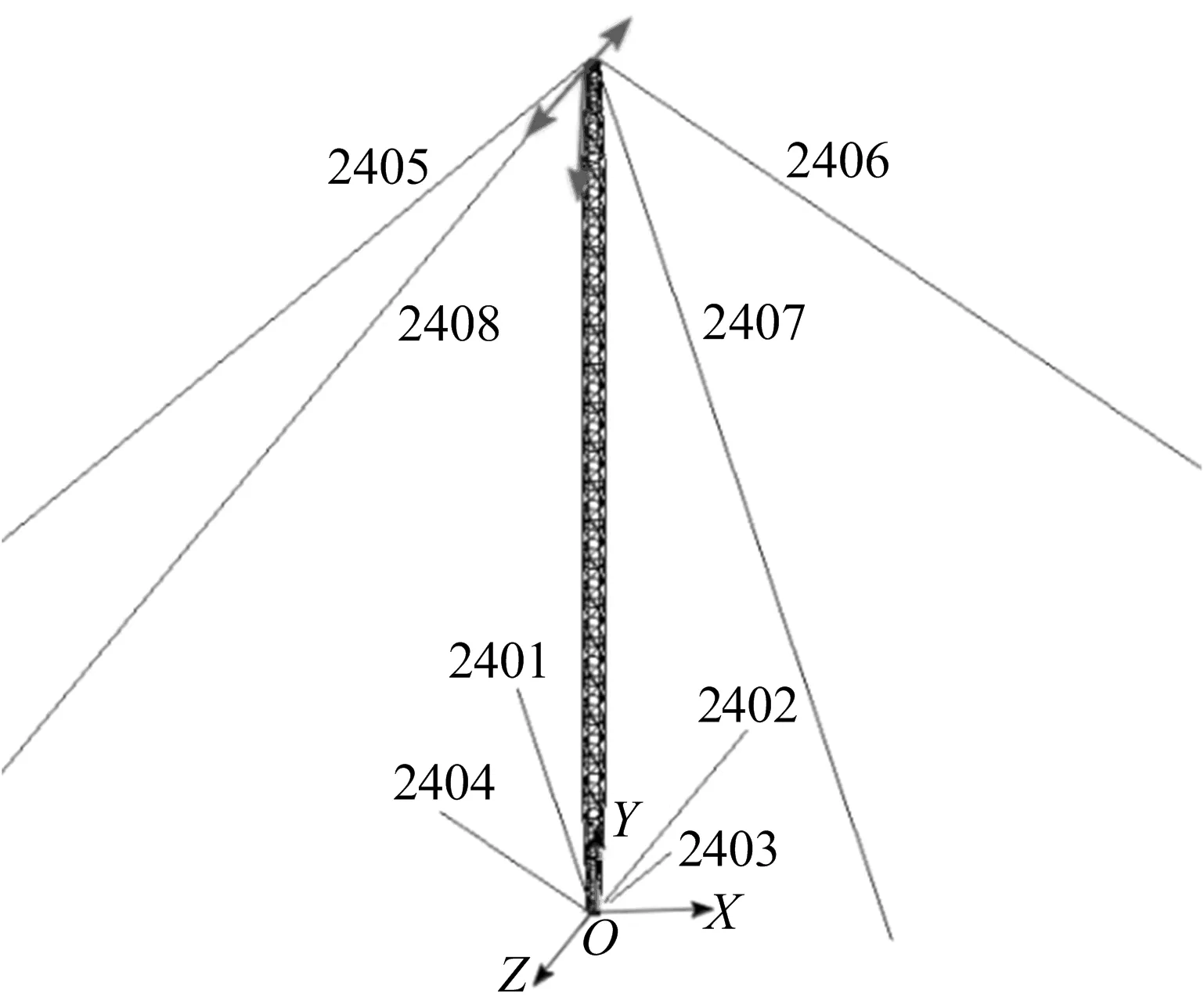
图3 抱杆有限元模型

2 风荷载模拟

采用线性滤波法模拟风速时程,风速谱采用Kaimal谱[3]。以安徽地区为例,地面粗糙类别为B类,地面粗糙度取0.03,10 m高度处的10 min平均风速取10 m/s(5级风)[4]。利用Matlab软件编程模拟得到不同高度处的风速时程曲线[5-6],94.3、110.3 m高度处脉动风速时程如图4所示。

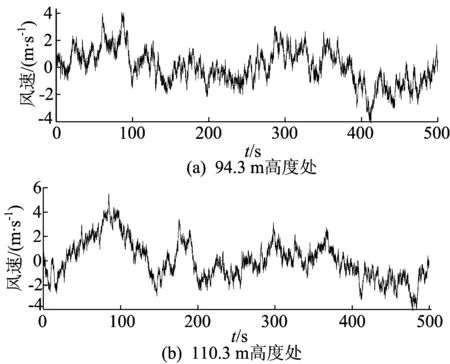
图4 94.3、110.3 m高度处脉动风速时程曲线

根据悬浮抱杆最大工作高度120 m,将其分为6段,上下锥段各1段,中间标准节分为4段,分别模拟各段中点所在高度处的风速时程。由于篇幅所限,仅列举了94.3 m高处、110.3 m高处(抱杆中段标准节2处高度)的脉动风速时程,2处高度对应抱杆位置如图5所示。

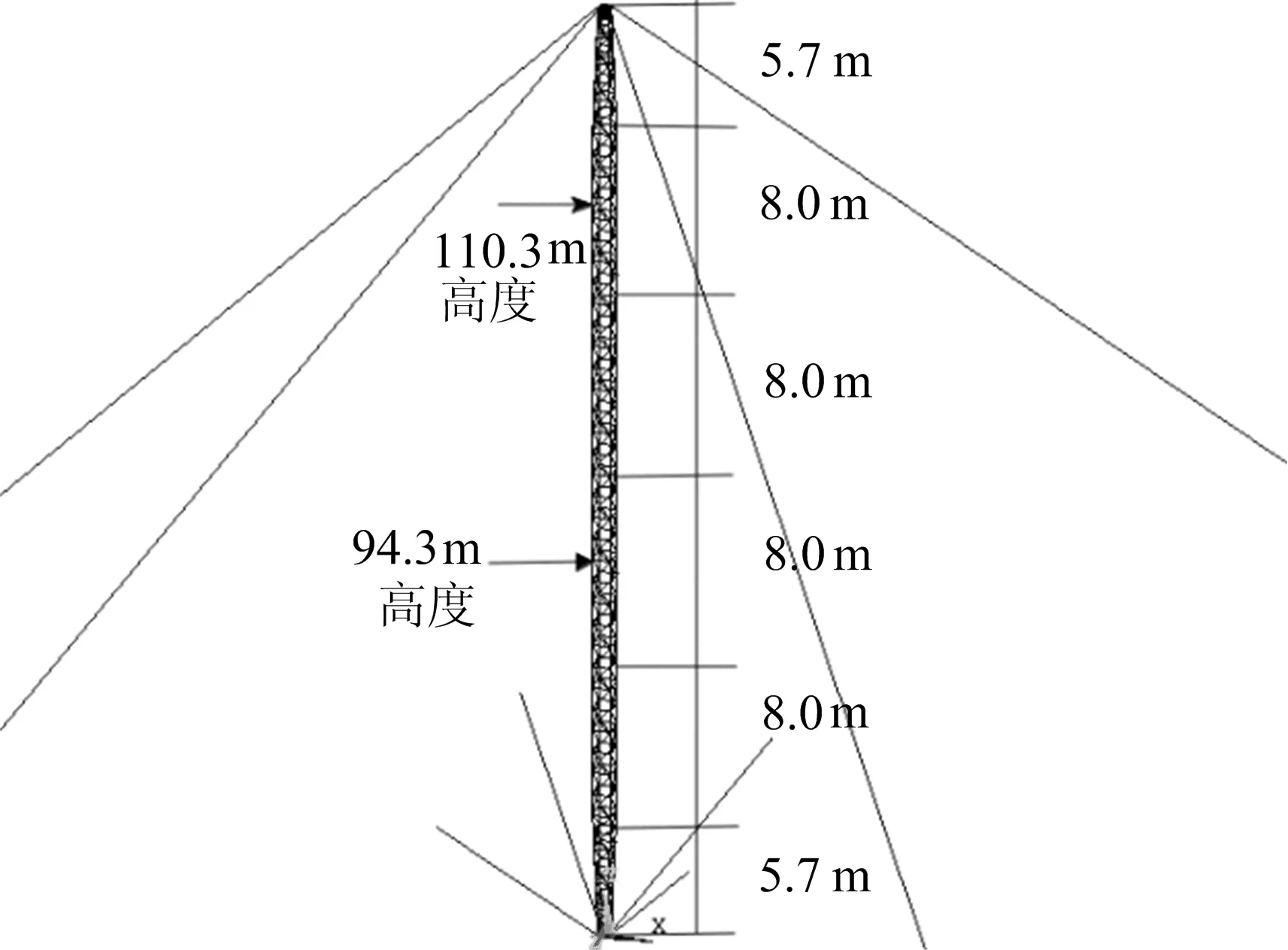
图5 94.3、110.3 m高度示意图

在t时刻,作用于抱杆i段的风荷载计算公式为:

(1)

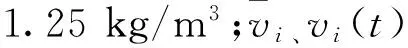
根据起重机设计规范[4],作用在抱杆上的工作状态下的风荷载计算公式为:

Pi=Cpi(t)Ai

(2)

于是,可以得出:

(3)

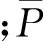
查起重机设计规范,取风力系数C=1.7,计算得到各段实体迎风面面积Ai,代入(3)式便可得到抱杆各段的风荷载时程曲线。

3 风振响应

3.1 模态分析

运用ANSYS的模态分析功能对建立的抱杆有限元模型进行模态分析,计算得到前5阶主要振型及固有频率。抱杆的各阶模态固有频率及周期见表1所列,前5阶模态振型如图6所示。

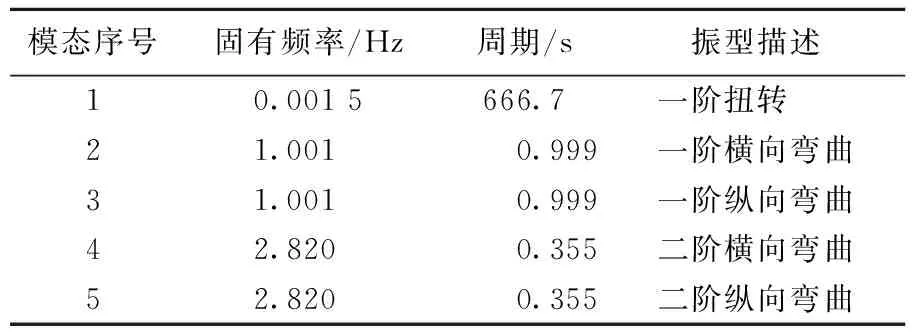
表1 结构固有频率及模态类型

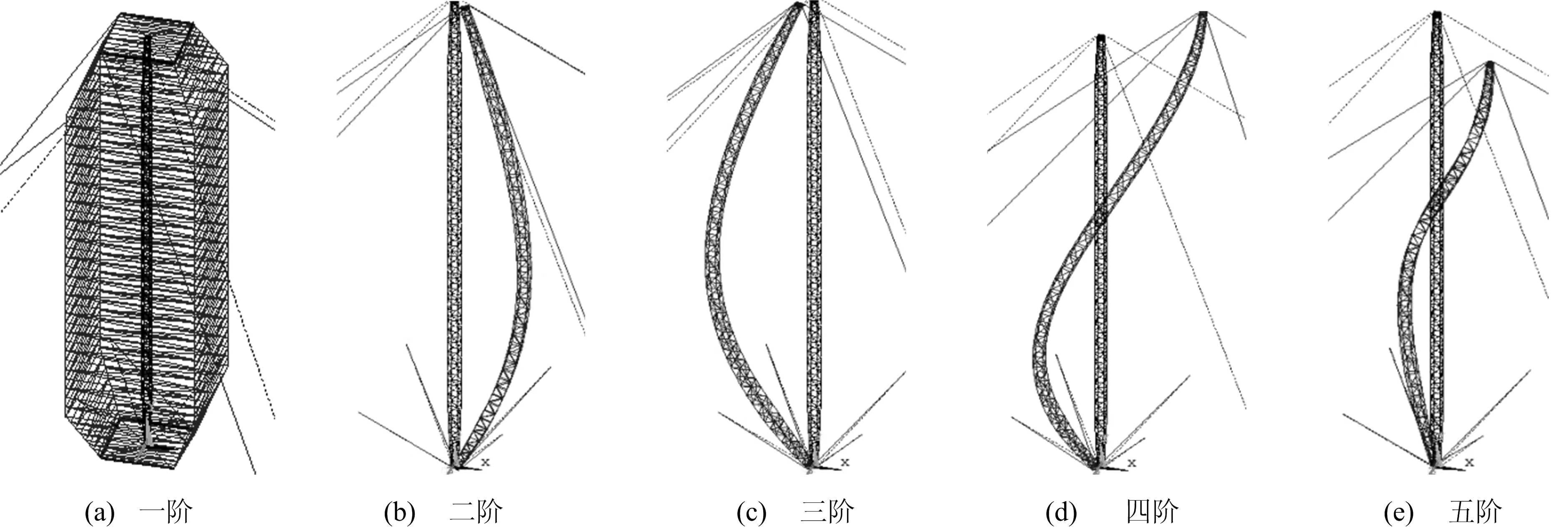
图6 抱杆前5阶模态

因为抱杆两端均由钢绞线连接,各点约束都可以看做铰接,抗扭刚度较差,所以导致一阶振型为扭转。实际工程中,需要通过给抱杆外拉线施加预紧力的方式来提高其整体抗扭刚度,从而达到抗扭的目的。又因为抱杆模型关于YOZ平面对称,所以二、三阶模态的固有频率相同,四、五阶模态同样如此。

3.2 位移时程分析

将模拟得到的风荷载时程,沿Z轴正向,以节点力的方式施加于结构迎风面的各节点。选取抱杆底部节点1、中部节点1291和顶部节点3599,通过ANSYS时间历程后处理,得到底部、中部、顶部位移时程,如图7所示。

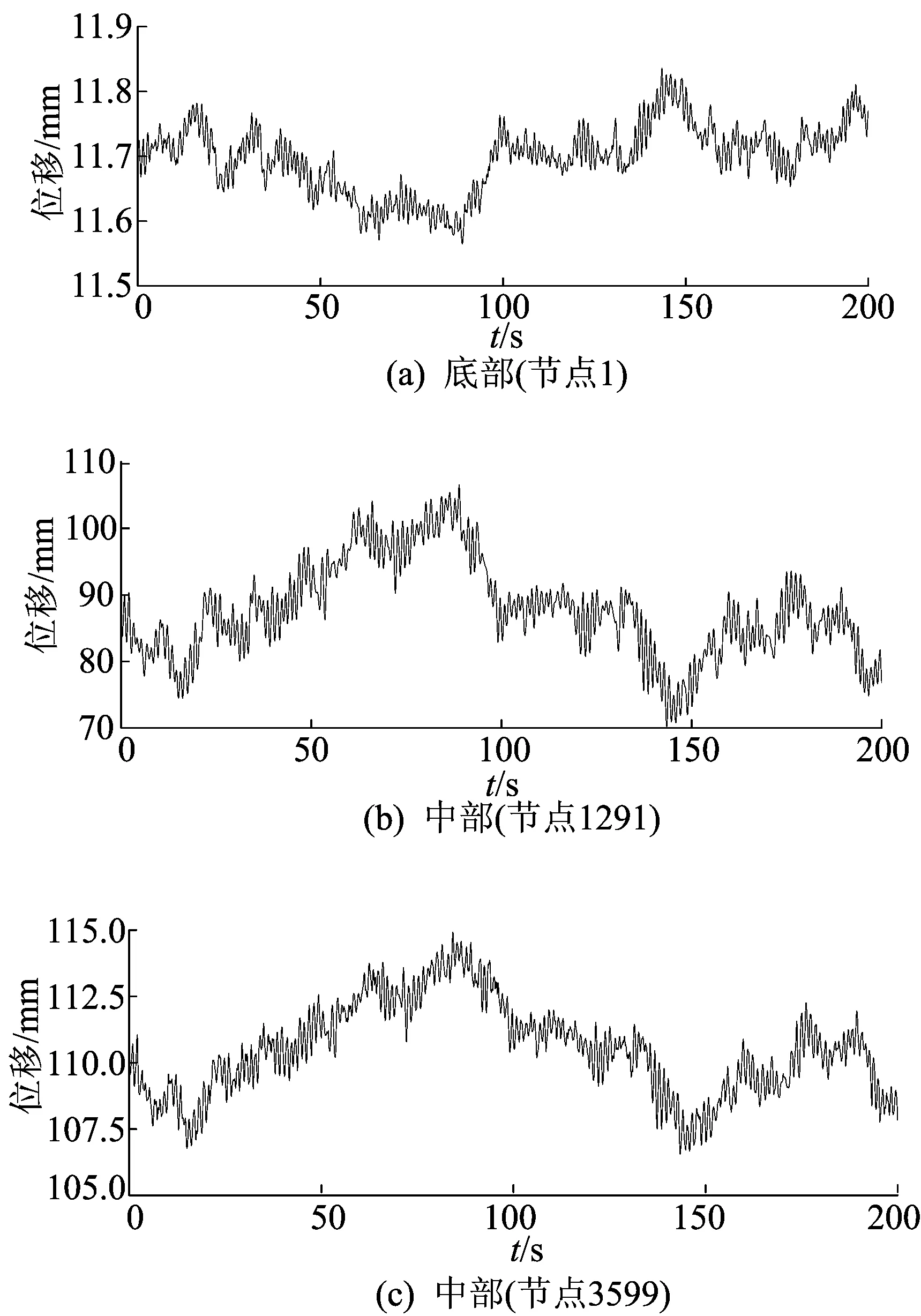
图7 各部分位移时程曲线

由于各点位移均取3个方向的合位移,抱杆在自重和吊重作用下,产生一个较大的位移,风荷载在此基础上施加于结构上。因此,各点位移均为正值,在自重和吊重作用下的平衡位置呈现往复振动形式。对比抱杆各部分位移时程可以看出,抱杆中、上部位移响应较大,底部位移响应较小。抱杆底部承托绳长度相对顶部外拉线较短,所以底部位移响应比顶部小很多,抱杆中部没有其他约束,因此位移响应也较大。建议施工过程中重点监测和控制抱杆的中、上部位移,以确保输电塔的施工安全。

本文将抱杆分为底部、顶部锥段各为1段,中部标准节平均分为8段,共10段,由下到上取11个节点,将200 s内各节点位移的平均值和仅脉动风荷载作用下的均方根值进行比较,各节点位移平均值和均方根值如图8所示。

从图8可以看出,位移平均值随着高度的增加而增大,说明抱杆在工作状态下中上部位移较大,底部位移较小。位移均方根值中间大两端小,说明在风荷载的作用下,抱杆中部振动幅度最大,越往两端振幅越小。抱杆设计和组装过程中,建议加强中间段标准节之间的连接,避免风振引起的标准节连接失效而造成的工程事故。

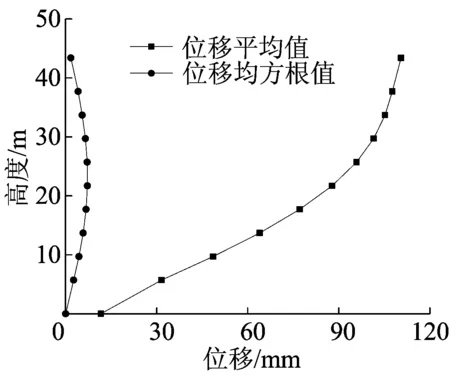
图8 节点位移平均值与均方根值

3.3 风振系数分析

风振系数β是指结构总响应(位移、荷载、内力、力矩)与平均风压引起的结构响应的比值,常用的风振系数有位移风振系数和荷载风振系数[7-8]。本文主要研究位移风振系数βDi,其定义式为:

(4)

其中,UDi、USi分别为动力位移和静力位移;μ为峰值保证因子,本文取3.0[9];σSi为仅脉动风荷载作用下节点i的动位移UDt的均方根值,其计算公式为:

(5)

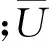
沿抱杆高度的风振系数分布如图9所示。

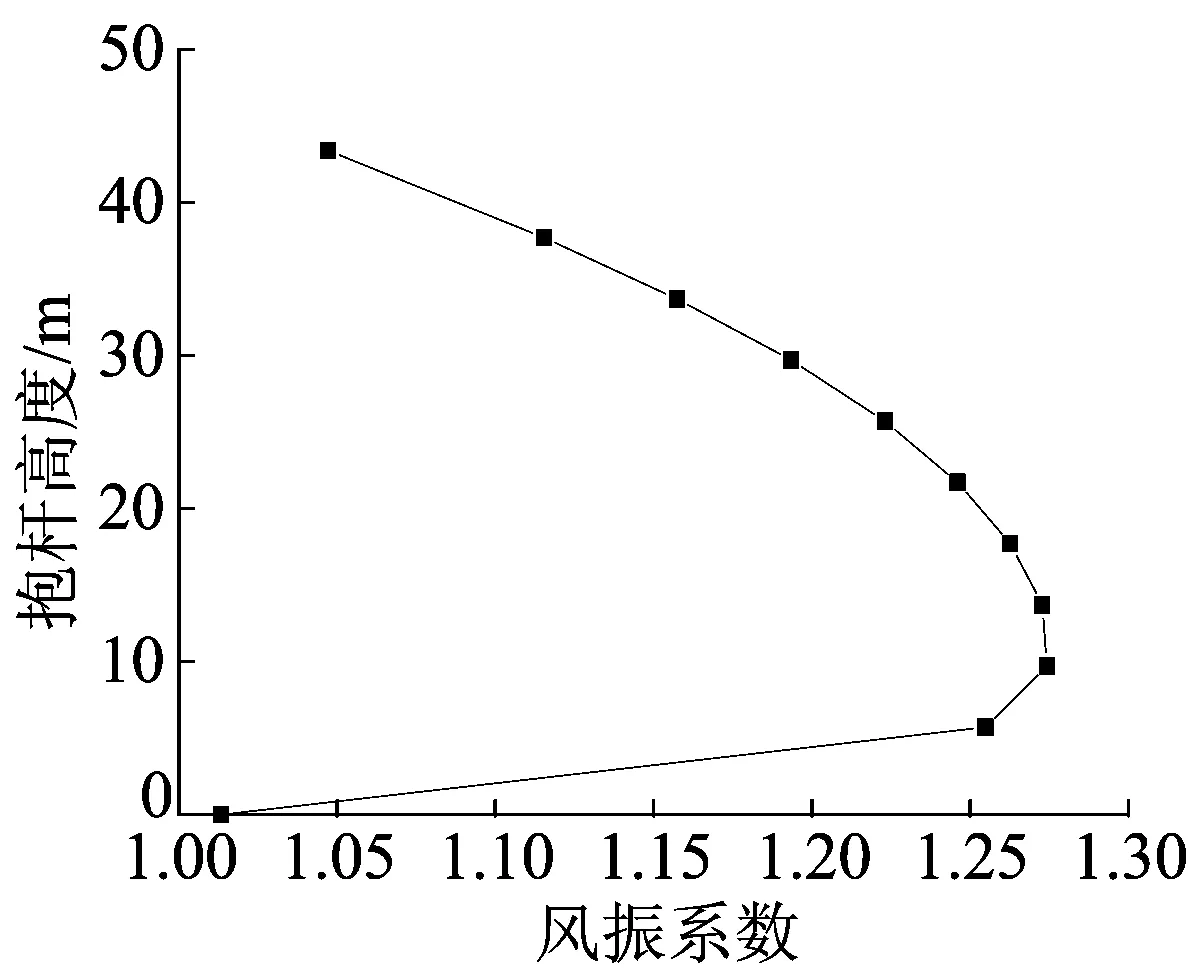
图9 抱杆各高度风振系数

抱杆在最大吊重80 kN、最大工作高度120 m状态下的位移风振系数见表2所列,由结果可以看出,抱杆各高度处的风振系数中间大两端小,这与抱杆两端采用的约束方式有关。其中,86.3 m高度处的风振系数最大,为1.28。根据计算结果,建议工作状态下,抱杆各高度处的风振系数均取1.3。

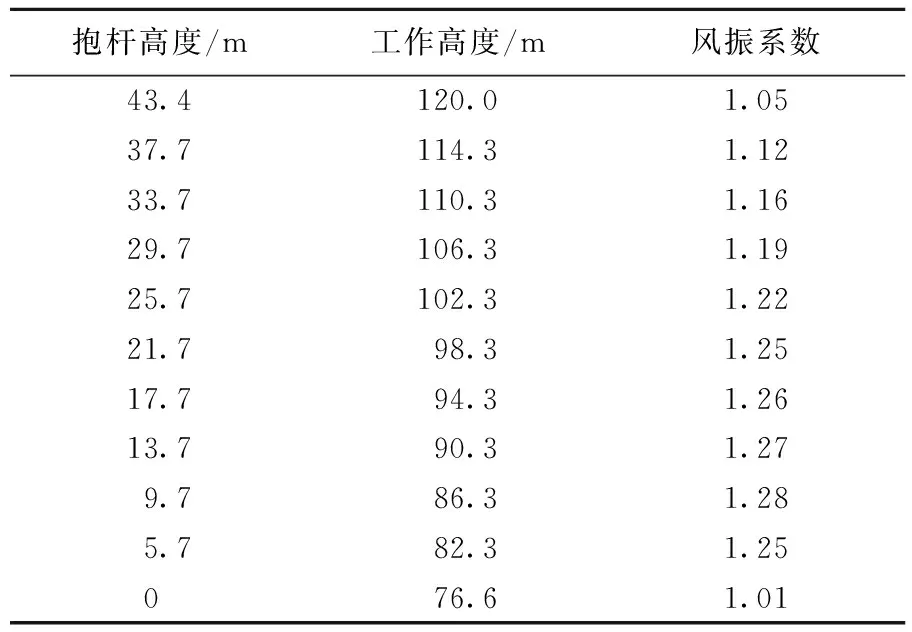
表2 抱杆各高度风振系数

4 结 论

本文基于线性滤波法,利用Matlab模拟各点风速时程,并运用ANSYS有限元软件对内悬浮外拉线抱杆进行风振响应分析,得到以下结论:

(1) 由模态分析结果可以得出,抱杆的抗扭刚度较弱,在抱杆的安装过程中,建议在外拉线和承托绳上施加预紧力,以提高其整体抗扭刚度。

(2) 工作状态下,抱杆中上部位移较大,底部位移较小。建议施工过程中重点监测、控制抱杆的中上部位移,以确保输电塔的施工安全。在风荷载作用下,抱杆中部振幅最大,越往两端振幅越小。在设计和组装抱杆过程中,应当加强中间段标准节之间的连接,避免风振引起的标准节连接失效而造成的工程事故。

(3) 工作状态下,抱杆各高度处的风振系数中间大两端小;根据计算结果,建议各高度处的风振系数均取1.3。

[1] DI PAOLA M.Digital simulation of wind field velocity[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74/75/76:91-109.

[2] 王新敏.ANSYS结构动力分析与应用[M].北京:人民交通出版社,2014:113-122.

[3] KAIMAL J C,WYNGAARD J C,IZUMI Y,et al.Spectral characteristics of surface-layer turbulence[J].Quarterly Journal of the Royal Meteorological Society,1972,98(417):563-589.

[4] 中国机械工业联合会.起重机设计规范:GB/T 3811—2008 [S].[S.l.:s.n.],2009:37-41.

[5] 徐赵东.土木工程常用软件分析与应用：MATLAB-SAP2000-ANSYS[M].北京:中国建筑工业出版社,2010:132-141.

[6] 侯铂,盛宏玉.巨型框架减振结构的脉动风模拟与风振时程分析[J].合肥工业大学学报(自然科学版),2012,35(6):790-793.

[7] 中华人民共和国住房和城乡建设部.建筑结构荷载规范:GB 50009—2012 [S].北京:中国建筑工业出版社,2012:57-60.

[8] 韩庆华,陈越,曾沁敏,等.大跨度球面网壳结构的风振系数研究[J].地震工程与工程振动,2007,27(1):38-45.

[9] 武岳,张建胜,陈波.结构风振极值分析中的峰值因子取值探讨[C]//中国空气动力学会.第七届全国风工程和工业空气动力学学术会议论文集.北京：科学出版社，2006:302-307.

(责任编辑 张淑艳)

Research on wind-induced response for inner suspended and outer guyed holding poles

XU Jincheng1, GENG Shuwei1, XIAO Feng2, ZHOU Huanlin1

(1.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China; 2.State Grid AC Engineering Construction Company, Beijing 100052, China)

The inner suspended and outer guyed holding pole is a kind of special hoisting machine which has been widely used in the electric industry. The holding pole has a large slenderness ratio and a special form of constraints, so it is necessary to analyze the wind-induced vibration response of the structure. Based on the linear filtering method, the fluctuating wind load is obtained by Matlab, and then it is applied to the model of the holding pole established by ANSYS to analyze the wind-induced response. The characteristic of wind-induced vibration of the holding pole is revealed and the wind-induced vibration coefficient of the holding pole in working condition is given. These results can provide a reference for the design and use of holding poles.

inner suspended and outer guyed holding pole; linear filtering method; wind-induced response; wind-induced vibration coefficient

2015-04-28；

2015-06-29

国家电网公司交流建设分公司科技资助项目(SGZB0000JLJS1400072)

徐金城(1989-),男,安徽肥东人,合肥工业大学硕士生; 周焕林(1973-),男,安徽宿松人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.11.019

TH212

A

1003-5060(2016)11-1531-05