挖掘机器人负载工况下的力与位姿控制

陈欠根, 高尚康, 赵喻明, 沈东羽

(1.中南大学 高性能复杂制造国家重点实验室,湖南 长沙 410083; 2.山河智能装备股份有限公司,湖南 长沙 410100)



挖掘机器人负载工况下的力与位姿控制

陈欠根1,2, 高尚康1, 赵喻明1,2, 沈东羽1

(1.中南大学 高性能复杂制造国家重点实验室,湖南 长沙 410083; 2.山河智能装备股份有限公司,湖南 长沙 410100)

文章分析了智能挖掘技术的研究现状,给出了试验挖掘机器人运动学模型及负载工况下动态特性方程;为实现典型挖掘工况下工作装置位姿及液压驱动力的控制,设计了一种基于BP(back propagation)神经网络PID(proportion-integral-derivative)控制算法的控制器;并以山河智能SWE-17E挖掘机器人为平台进行试验验证。试验结果表明,采用BP神经网络PID控制算法得到的工作装置末端轨迹跟踪误差均方差小于10 cm,驱动力跟踪也达到了较高精度,证明了BP神经网络PID控制算法对于挖掘机器人力与位姿控制的可行性和有效性。

挖掘机器人;典型挖掘工况;BP神经网络PID控制;力与位姿控制

液压挖掘机是一种集多功能于一身的工程机械,其结构复杂、应用广泛,在工业、农业、国防等领域都能发挥重要作用。随着工程机械行业技术的发展,机电液一体化和智能化越来越多地与工程机械相结合。液压挖掘机作为最典型的工程机械,其智能化控制一直是世界各国研究者关注的焦点。文献[1]采用了有别于传统PID(proportion-integral-derivative)控制算法的PID算法对液压挖掘机进行轨迹控制;文献[2]对液压挖掘机的负载阻力模型和参数辨识进行了较为深入的研究;文献[3]设计了一种自校正调节器，对液压挖掘机工作装置进行运动控制研究;文献[4]将神经网络控制运用于空载情况下的挖掘机轨迹控制。

本文利用BP(back propagation)神经网络PID控制算法良好的自适应性及非线性映射能力[5],将其应用于黏土挖掘工况下挖掘机器人的末端轨迹跟踪控制和液压驱动力的跟踪控制；并以山河智能SWE-17E型挖掘机器人为试验平台,阐明挖掘机工作装置的运动学特性和负载工况下动力学特性；以典型的满斗挖掘工作循环为分析对象,验证了BP神经网络PID控制算法对于智能挖掘中力与位姿控制的有效性与控制精度。

1 挖掘机器人的运动学模型

挖掘机的工作装置类似于机器人的各个关节。本文以自动挖掘的一个典型实际挖土作业过程作为试验对象,暂不考虑上车平台的回转(θ0=0),因此整个工作装置可视为一个三自由度机器人系统。工作装置的运动学模型如图1所示。

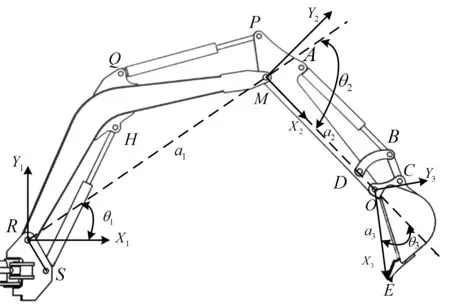
图1 工作装置运动学模型

图1中,分别在每个关节铰点处建立1个坐标系,根据D-H坐标变换可以得出工作装置末端相对于机身坐标原点的位置,限于篇幅和研究侧重点,本文不给出具体的运动学方程推导过程,直接给出铲斗齿尖位置P=[xyz]T和工作装置转角θi的关系,即

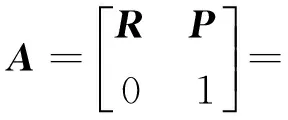
(1)

其中,R为铲斗末端姿态矩阵;a1、a2、a3分别为动臂、斗杆与铲斗的关节长度;Si=sinθi,Sij=sin(θi+θj),Sijk=sin(θi+θj+θk);Ci、Cij、Cijk为形式类同的余弦关系。

由给定末端轨迹坐标可得出各个关节角度θ1、θ2、θ3,而工作装置液压缸长度λ1、λ2、λ3与关节角度值有对应关系,表示为λn=λ(θn)。通过路径规划策略可得任意时刻各个关节转角,再根据液压缸长度与关节转角关系式调节液压缸长度使各个工作装置运动到目标角度。

2 负载工况下系统动态特性分析

试验平台电液比例系统采用的是博世力士乐公司的负载独立流量分配系统(LUDV)[6],多个执行机构可以同时动作,流量与负载无关,因此在负载挖掘过程中动态负载不断变化的工况下仍然可以独立地分配驱动机构流量与压力,实现驱动力的跟踪匹配。

在实际工作中,铲斗直接与负载接触,其工作装置液压活塞杆的实际驱动力[7]为:

F=P1A1-P2A2

(2)

其中,P1、P2分别为无杆腔和有杆腔时的液压油压力;A1、A2分别为无杆腔和有杆腔时活塞杆的有效作用面积。

负载工况下挖掘机工作装置的动力学特性方程[8]可以表示为:

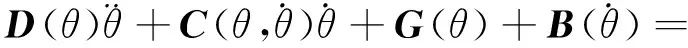
(3)

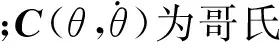
由于土壤内在因素的不确定性及土壤阻力计算的复杂性,一般采用如下经验公式[9]估算挖掘阻力切向分力,即

(4)

其中,C为土壤硬度系数,本文取值为5～8;R为铲斗关节的切削半径;φmax为铲斗从入土到出土总转角的一半;φ为铲斗关节瞬时转角;B为铲斗切削刃宽度影响系数,B=1+2.6b,b为铲斗平均宽度;A为切削角变化影响系数,取为1.3;Z为斗齿影响系数,Z=0.75;X为斗侧壁影响系数,可取X=1.15;D为切削刃挤压土壤的力的大小,可根据斗容量大小选取适当的值。

本文研究中试验土壤为Ⅱ级土壤,土质均匀。根据经验表明,Fn/Ft∈[0.1～0.26],常取Fn=0.2Ft,方向则随机变化,一般为了简化计算,允许Fn=0。将求得的挖掘阻力代入到工作装置的动力学方程(3)中,在其他参数已知的前提下,可以求出理想的液压驱动力Fd。

3 控制器设计

在挖掘机器人的实际挖土作业中,既要控制挖掘力的大小,使得液压缸提供的驱动力能够满足挖掘需求却不超过工作装置的强度极限范围,又要准确控制工作装置的位姿,从而实现对目标轨迹的准确跟踪。传统PID控制器一般只适应于线性系统,难以满足动态系统的控制要求,本文采用BP神经网络PID控制方法来实现智能挖掘过程中力与位姿的控制。

3.1 控制系统整体结构

在一个动态系统中,PID控制要取得良好的控制效果,就必须不断调整比例、积分、微分3个参数,从变化无穷的组合中找出最佳组合。结合BP神经网络是为了在挖掘机器人运行过程中,根据系统动态特性和运行情况,通过BP神经网络自学习能力和权系数的调整来整定PID控制的3个参数,使得控制器能够以某种最优控制率逼近控制目标。

控制系统整体结构如图2所示。

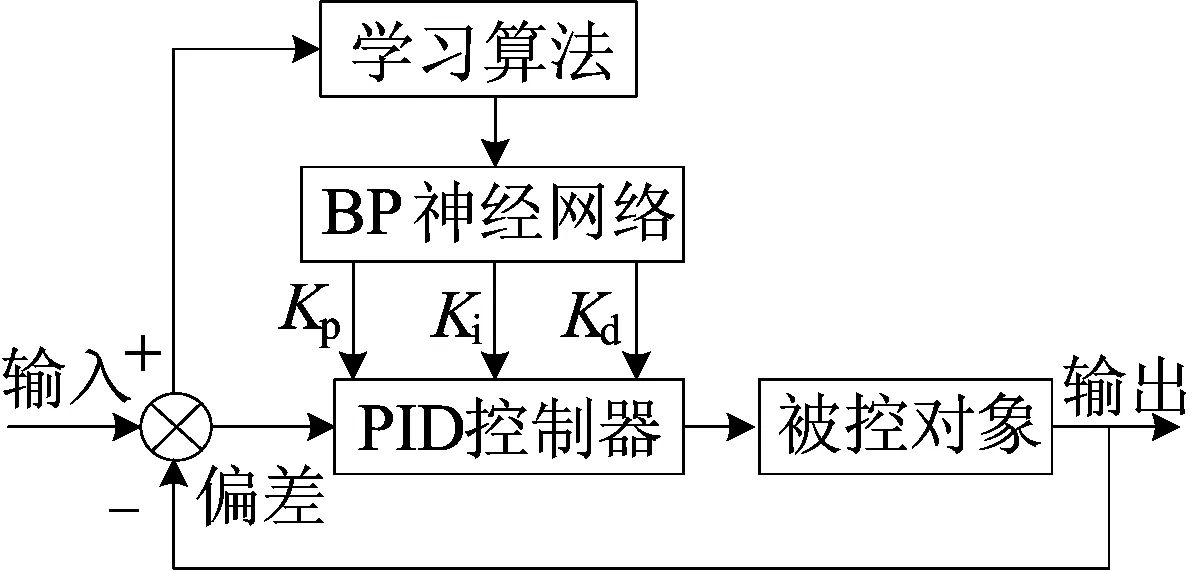
图2 控制系统整体结构

3.2 控制器的神经网络结构

系统采用3层BP神经网络,一般分为输入层、隐含层和输出层。

神经网络输入层的输入为:

(5)

其中,被控对象越复杂,神经元个数M越多,本文取M为6;角度值的3个输入量分别为关节角度设定值θd、角度的实际值θ、角度的设定值与实际值之间的误差eθ(eθ=θd-θ);活塞杆驱动力的3个输入量为理想驱动力Fd、实际驱动力F、理想驱动力与实际驱动力的误差eF(eF=Fd-F)。

BP神经网络整体结构如图3所示。其中,驱动力设定值即为理想驱动力Fd。

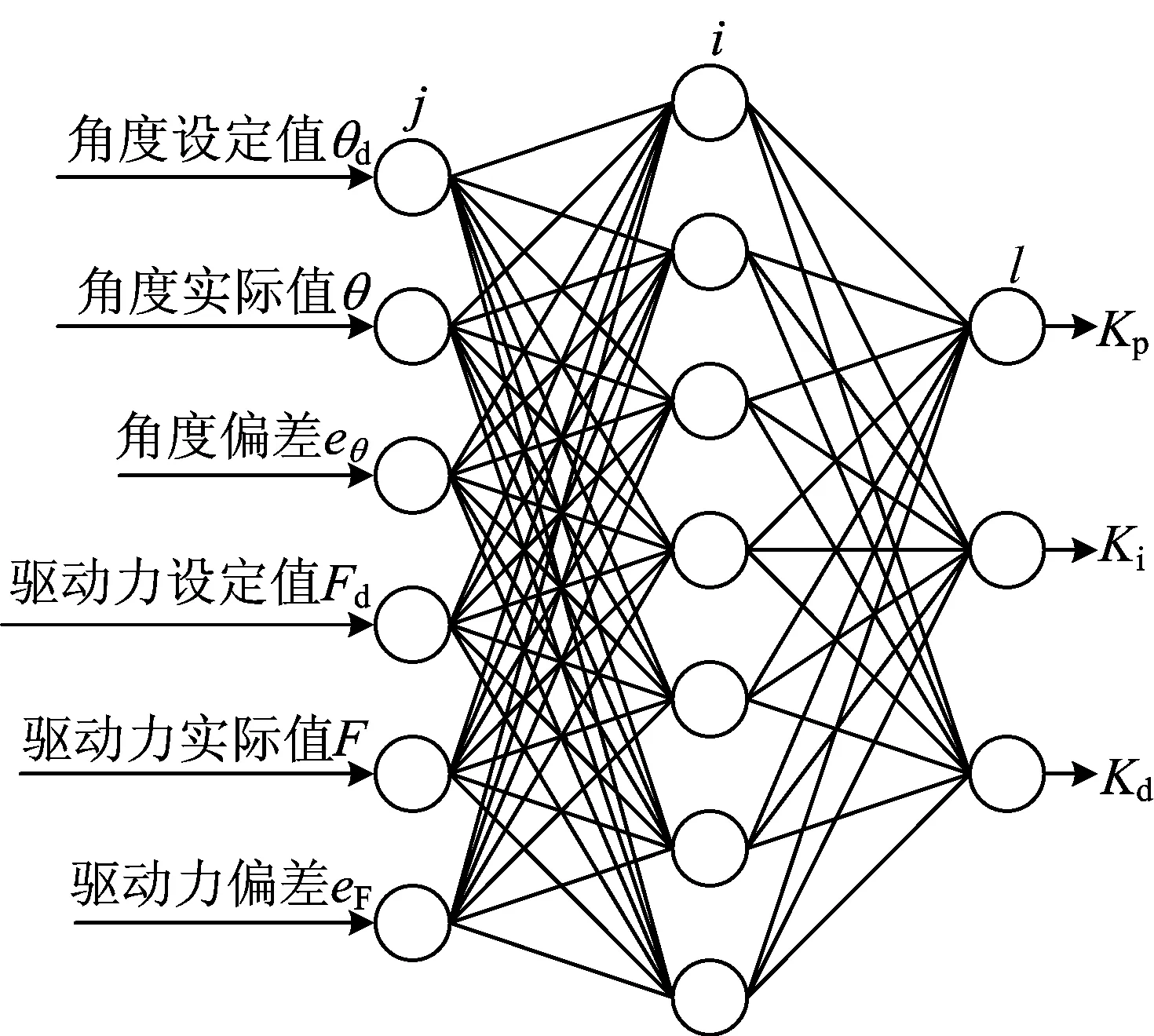
图3 BP神经网络整体结构

网络隐含层的输入和输出分别为:

(6)

(7)

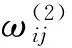
(8)

网络输出层的输入和输出分别为:

(9)

(10)

(11)

网络输出层中,输出节点个数取为3,分别对应PID的3个参数Kp、Ki、Kd,神经元激活函数取非负的Sigmoid函数，即

(12)

3个网络层依次确定后,神经网络结构确定为6-7-3结构。性能指标函数取为:

(13)

由于经典BP神经网络结构收敛速度慢,容易收敛到局部最优[10],因此需要适当改进。本文采用附加惯性项的优化方法,使得网络能够快速收敛到全局最优。由此带来的计算误差可通过调整学习算法进行补偿。

根据以上分析,将网络输出层的学习算法进行调整如下:

(14)

(15)

其中,η为学习速率;α为惯性系数。按同样的方法可以调整网络隐含层权值的学习算法。

4 黏土挖掘试验研究及分析

本研究以山河智能装备股份有限公司生产的SWE-17E挖掘机器人为实际控制对象,以挖掘机器人的准备—入土—满斗挖掘—出土—卸土为控制过程，对SWE-17E液压挖掘机进行改造。同时,在各关节铰点处安装角度传感器，在工作液压缸进出油口安装压力传感器,通过传感器实时监测并反馈数据信号。

试验过程中，由上位机根据预定的挖掘轨迹和满斗挖掘过程中理想的挖掘力规划相应的设定角度和驱动力,下位机通过角度传感器和压力传感器实时监测各个关节角度值和工作油缸的大小腔压力值。在VB编程界面将BP神经网络PID控制算法做成控制模块嵌入控制系统中,对角度值和驱动力的误差进行计算分析,再根据BP神经网络PID控制算法来整定PID参数,通过控制系统向执行机构发出相应的控制信号,改变阀芯位移和阀口开度来控制工作装置的位姿以及电液系统提供的驱动力,从而实现对智能挖掘典型挖掘过程中力与位姿的跟踪控制。

试验所用土壤为湿软黏土,属Ⅱ级土壤,符合液压挖掘机实际工程作业的一般工况。应用BP神经网络结构,令神经网络的学习速率η=0.28,惯性系数α=0.04,加权系数初始值随机选值,取值区间为[-0.5,0.5]。工作装置末端驱动力跟踪曲线如图4所示。由图4可知,采用BP神经网络PID控制能对驱动力进行较为准确的跟踪。动臂、斗杆、铲斗角度跟踪曲线如图5所示。齿尖轨迹跟踪曲线如图6所示。

图4 驱动力跟踪曲线

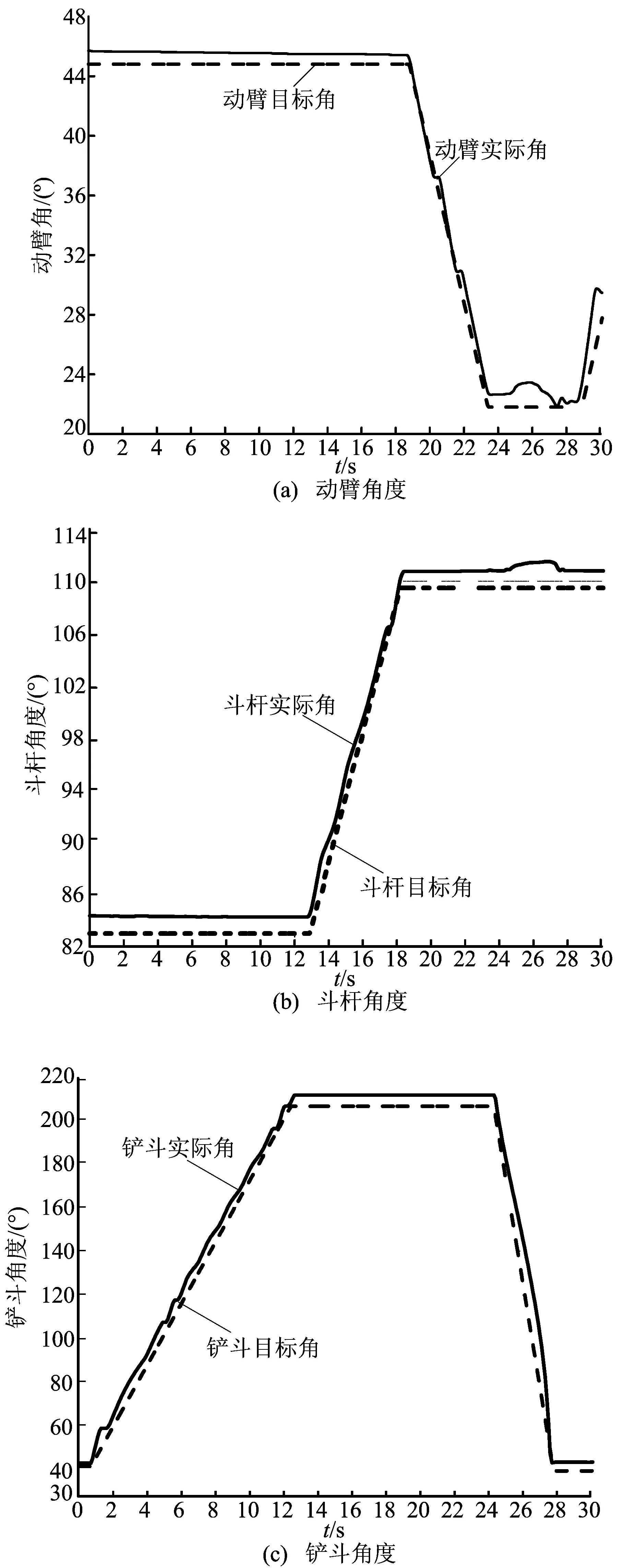
图5 动臂角度、斗杆角度以及铲斗角度跟踪曲线

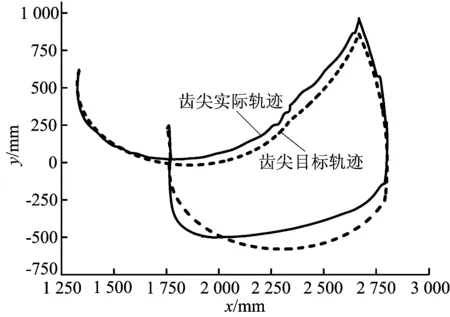
图6 齿尖轨迹跟踪曲线

由图5可知,角度跟踪的最大误差分别小于3°、4°、10°,由于各关节角度误差存在一定的补偿和叠加关系,使得末端齿尖轨迹跟踪的最大误差控制在15 cm之内,误差均方差小于10 cm。

5 结 论

(1) 本文分析了国内外智能挖掘技术的研究现状,在已有基础上建立挖掘机器人工作装置的三自由度运动学模型,并给出了负载工况下的系统动态特性方程。

(2) 基于BP神经网络PID控制算法设计了能够实现挖掘机器人工作装置姿态控制及末端执行机构驱动力跟踪的控制器。

(3) 以山河智能SWE-17E挖掘机器人为平台,对本文设计的控制器进行试验论证。试验结果表明:在Ⅱ级湿软黏土工况下,工作装置末端即齿尖路径跟踪的误差均方差小于10 cm,驱动力也能实现准确跟踪,证明了BP神经网络PID控制算法对于挖掘机器人力与位姿控制的可行性和有效性。

[1] GU J,TAYLOR J,SEWARD D.Proportional-integral-plus control of an intelligent excavator[J].Computer-Aided Civil and Infrastructure Engineering,2004,19(1):16-27.

[3] 张大庆.液压挖掘机工作装置运动控制研究[D].长沙:中南大学,2006.

[4] 吕广明,孙立宁,薛渊.神经网络在液压挖掘机工装轨迹控制中的应用[J].机械工程学报,2005,41(5):119-122.

[5] BERGMANN S,STELZER S,STRASSBURGER S.On the use of artificial neural networks in simulation-based manufacturing control[J].Journal of Simulation,2014,8(1):76-90.

[6] 蒋道成,于兰英,柯坚,等.LUDV控制系统的动态仿真[J].机械工程师,2008(4):27-29.

[7] 张大庆,赵喻明,刘心昊,等.液压挖掘机四自由度自适应控制[J].华中科技大学学报(自然科学版),2013,41(增刊1):455-458，470.

[8] 佘翊妮.基于多体动力学的大型正铲液压挖掘机工作装置的动态特性研究[D].杭州:浙江工业大学,2013.

[9] 刘静.挖掘机器人虚拟样机建模技术及其应用研究[D].杭州:浙江大学,2005.

[10] 卢建中,程浩.改进GA优化BP神经网络的短时交通流预测[J].合肥工业大学学报(自然科学版),2015,38(1):127-131.

(责任编辑 胡亚敏)

Research on force and position and pose control of mining robot under load condition

CHEN Qian’gen1,2, GAO Shangkang1， ZHAO Yuming1,2， SHEN Dongyu1

(1.State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China; 2.Sunward Intelligent Equipment Co., Ltd., Changsha 410100, China)

The kinematic model and dynamic characteristic equation of mining robot under load condition were introduced based on the analysis of research status about intelligent mining technology. To realize the position and pose control of working device and the hydraulic driving force control under typical mining condition, a controller based on the proportion-integral-derivative(PID) control algorithm with back propagation neural network(BP-NN) was designed. The test was conducted on the basis of SWE-17E mining robot of Sunward. The experimental results show that the end-effector trajectory tracking error of working device is less than 10 cm, and the tracking of driving force also has high accuracy, demonstrating that the PID control algorithm with BP-NN is feasible and effective in force and position and pose control of mining robot.

mining robot; typical mining condition; proportion-integral-derivative(PID) control with back propagation neural network(BP-NN); force and position and pose control

2015-06-08；

2015-09-08

国家“十二五”科技支撑计划资助项目(2013BAF07B02)

陈欠根(1956-),男,江西新干人,中南大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.11.003

TU621;TP183

A

1003-5060(2016)11-1451-05