图形变换的规律研究与实践

江苏省扬州市方陵区头桥中学(225109)

陈利明●



图形变换的规律研究与实践

江苏省扬州市方陵区头桥中学(225109)

陈利明●

本文图形的平移、翻折和旋转问题是运用运动观点、运动思想去研究图形位置变化或图形性质的数学问题.这类问题一般有两种情况：①根据条件中的图形运动，研究图形在运动过程中或经过运动后的位置与相关性质；②条件中没有提到图形运动，要利用运动的思想添加辅助线，发现隐含条件，解决问题.

平移；翻折；旋转

在图形的平移、翻折与旋转运动变化中寻找不变的量；对应边相等，对应角相等.把握规律，探究关系，要学会把图形的对称性与分类讨论的数学思想结合在一起.

一、图形的平移

在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移.平移特征：图形平移时，图形中的每一点的平移方向都相同，平移距离都相等.

实践1 在△ABC,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD，再将线段BD平移到EF，使点E在AB上，点F在AC上.(1)如图1，直接写出∠ABD和∠CFE的度数；(2)在图1中证明AE=CF；(3)如图2，连接CE，判断△CEF的形状并加以证明.

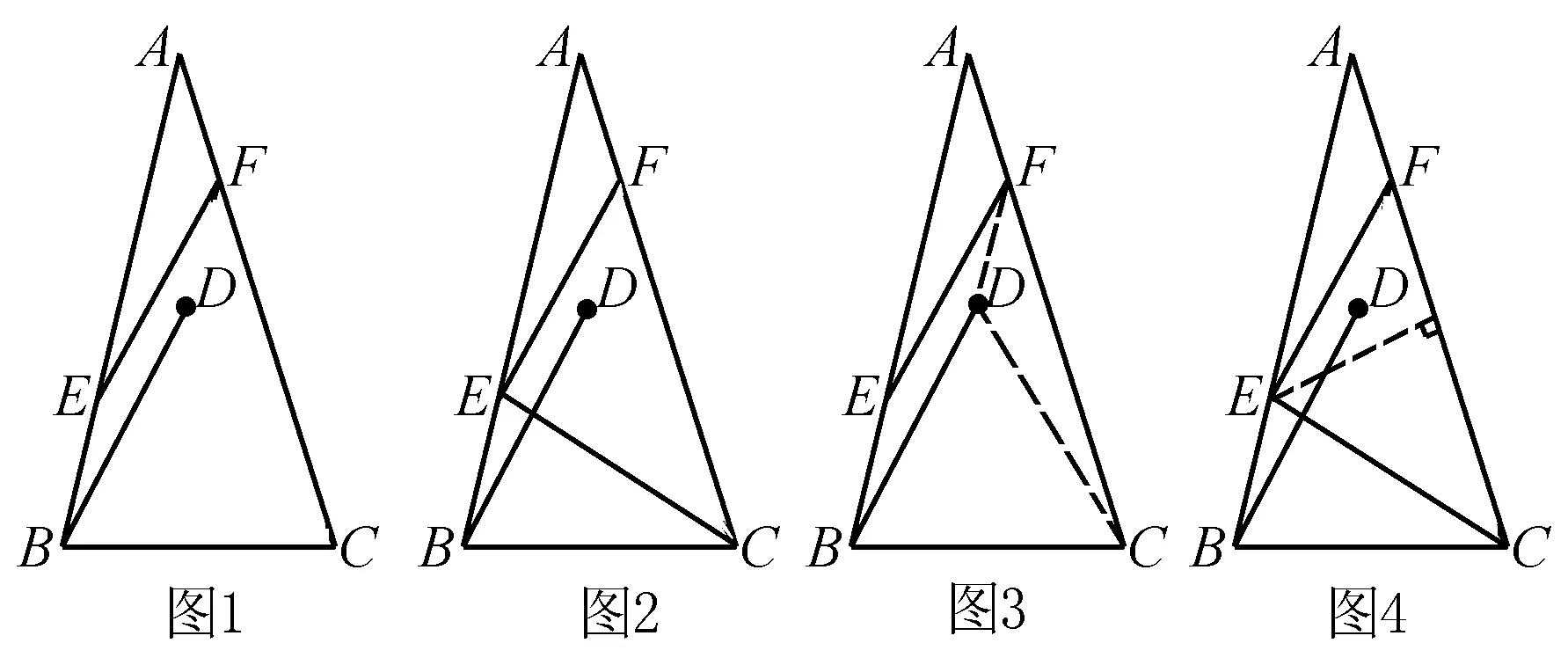
解析 (1)∠ABD=15°,∠CFE=45°.

(2)连接CD、DF，如图3所示.

∵线段BC绕点B逆时针旋转60°得到线段BD ∴BD=BC,∠CBD=60° ∴△BCD是等边三角形.∴CD=BD.

∵线段BD平移到EF，∴EF∥BD,EF=BD.

∴四边形BDFE是平行四边形 ∴EF=CD.

∵AB=AC,∠A=30° ∴∠ABC=∠ACB=∠75°.

∴∠ABD=∠ABC-∠CBD=15°=∠ACD,

∴∠DFE=∠ABD=15°,∠AFE=∠ABD=15°.

∴∠AEF=∠ACD=15°.

∵∠CFE=∠A+∠AEF=30°+15°=45°,

∴∠CFD=∠CFE-∠DFE=45°-15°=30°,

∴∠A=∠CFD=30° ∴△AEF≌△FCD ∴AE=CF.

(3)△CEF是等腰直角三角形.

证明如下：如图4，过点E作EG⊥CF于点G.

∵∠CFE=45° ∴FEG=∠45° ∴EG=FG.

二、图形的翻折

翻折是指把一个图形按某一直线翻折180°后形成的新的图形的变化.解这类题要抓住翻折前后两个图形是全等的，弄清翻折后不变的要素.

实践2 如图5将一张三角形纸片ABC折叠，使点A落在BC边上，折痕EF∥BC，得到△EFG;再继续将纸片沿△BEG的对称轴EM折叠，依照上述作法，再将△CFG折叠，最终到矩形EMNF，折叠后△EMG和△FNG的面积分别为1和2，则△ABC的面积为( ).

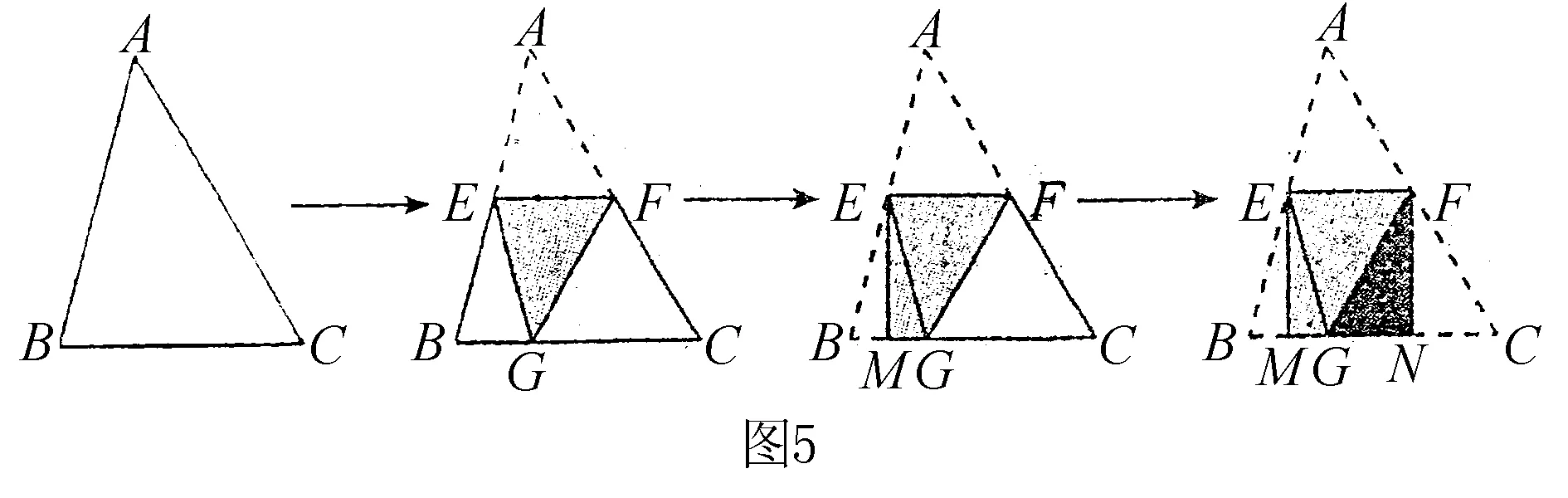
解析 根据折叠的性质可知，△AEF≌△GEF,△EBM≌△EGM,△FCN≌△FGN.则△ABC的面积为矩形.

三、图形的旋转

在平面内，将一个图形绕一个定点沿某个方向转动一个角度成为与原来相等的图形，这样的图形运动叫做图形的旋转，这个定点叫作旋转中心，图形转动的角叫作旋转角.旋转特征：图形旋转时，图形中的每一点旋转的角都相等，都等于图形的旋转角，旋转也是图形的一种基本变换，通过图形旋转变换将一些简单的平面图形按要求旋转到适当的位置，使问题得到简单的解决，它是一种重要的解题方法.

实践3 在平面直角坐标系中，O为原点，点A(-2，0)，点B(0，2)，点E，点F分别为OA，OB的中点.若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′,记旋转角为α.

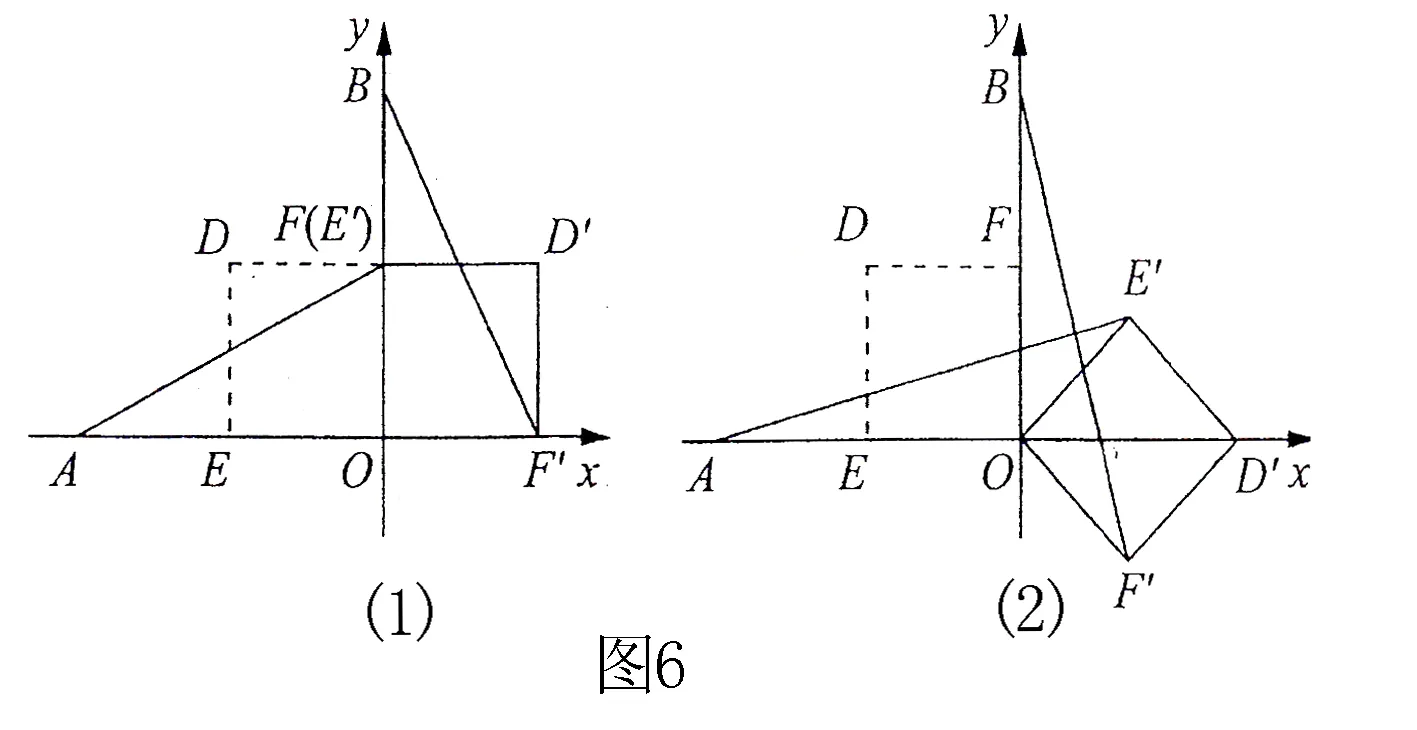
(1)如图6(1)所示，当α=90°时，求AE′,BF′的长；(2)如图6(2)所示，当α=135°时，求证AE′=BF′,且AE′⊥BF′.

G

B