应用转化的数学思想解题讨论
江苏省扬州市广陵区头桥中学(225109)
朱胜杰●
应用转化的数学思想解题讨论
江苏省扬州市广陵区头桥中学(225109)
朱胜杰●
转化和化归的思想就是在研究和解决数学问题时采用某种方式,借助某些图形性质、公式或已知条件将问题通过变换加以转化,进而达到解决问题的目睥.转化和化归思想是初中数学中常见的一种数学思想方法,它的应用十分广泛,我们在解题时经常运用此思想方法,将复杂问题转化成简单问题,将生疏的问题转化成熟悉的问题.转化和化归的思想就是要我们深刻理解并灵活运用新旧知识之间的关系.
转化;分式方程;增根
本文通过实例研究应用转化思想解题.
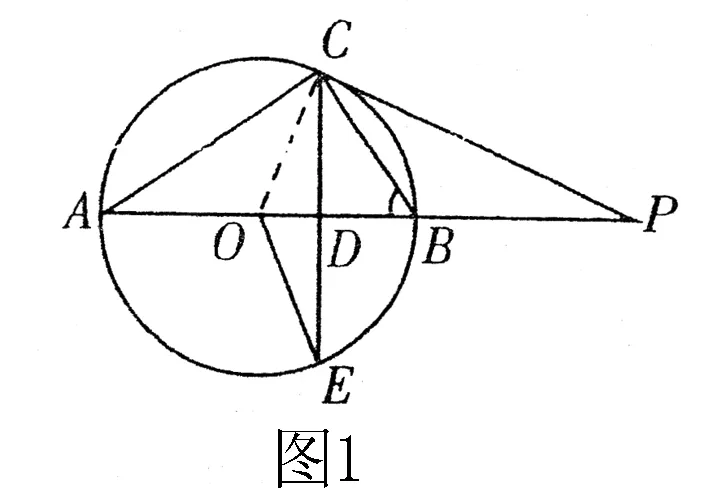
例1 如图1所示,AB是⊙O的直径,点P在AB的延长,弦CE交AB于D点,连接OE,AC,BC,已知∠POE=2∠CAB,∠P=∠E.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径及tan∠P的值.
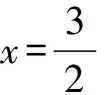
分析 对于分式方程,我们是将其转化为整式方程求解,转化的途径是去分母,也就是用分式方程中各分式的最简公分母去乘以方程的两边,化为整式方程,但这样的转化得到的整式方程可能与原方程不一定同解,有可能产生增根,因此解分式方程时必须对求出的解进行验根.
方程两边都乘以x(x+2)(x-2),得(x-4)(x-2)=x+2-2x.
整理后,得x2-5x+6=0,(x-2)(x-3)=0,解得x1=2,x2=3.
经检验,x=3是原方程的根,x=2是增根,应舍去.
检验的方法有两种,一种方法是将所求出的未知数的值代入原方程两边进行检验,两边相等则是原方程的解,两边不相等则是增根,另一种方法是把变形后所得的整式方程的根代入所乘的整式,如果代入后这个整式为零,这个根就是原方程的增根,如果代入后这个整式不为零,这个根就是原方程的根.
转化思想贯穿于数学的始终,三角函数的定义、解直角三角形的前提是在直角三角形中,而通常给出的是斜三角形、四边形(特别是梯形),因此解题时,常常通过作高(或垂线)将斜三角形、四边形转化为直角三角形的问题,此外,在实际应用时,首先将实际问题转化为数学模型,再借助于解直角三角形的知识求解.
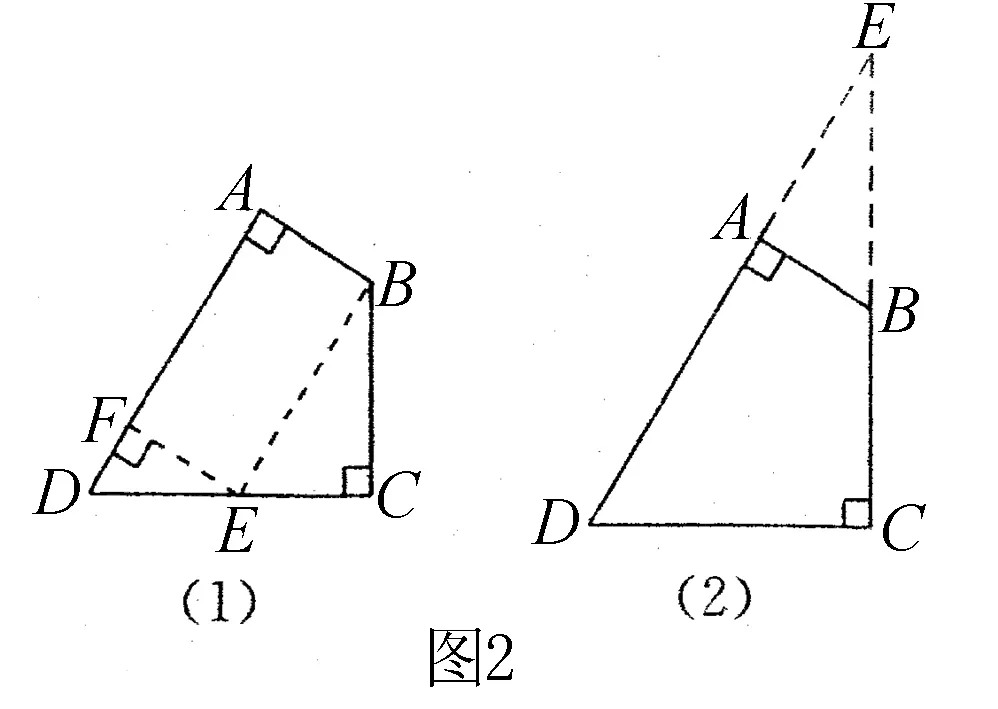
本题求不规则图形的面积要转化为角直角三角形或特殊的四边形的面积来求.
解法1 如图2(1)所示,过点B作BE∥AD交CD于点E,过点E作EF∥AB交AD于点F,则BE⊥AB,EF⊥AD ∴四边形ABEF是矩形 ∴∠CBE=120°,90°30°,∠D=180°-120°=60°.
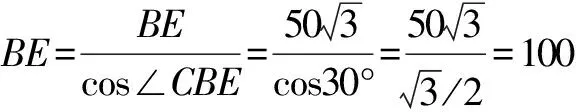

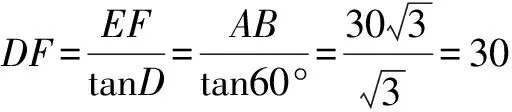

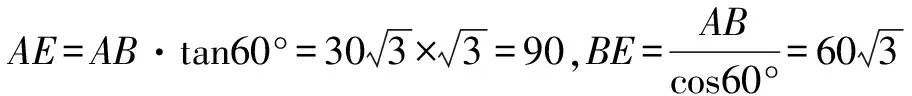
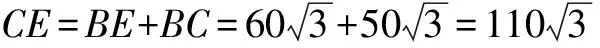
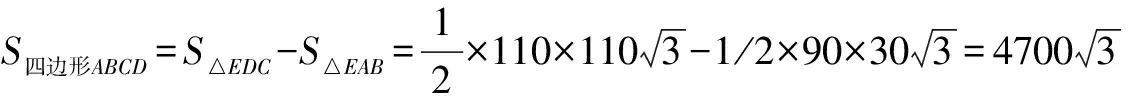
此题给出了两种不同的解答方法,一是适当添加辅助线,把不规则四边形转化为直角三角形和直角梯形求解;二是通过补形,把不规则四边形转化为直角三角形.两种方法的实质是将四边形问题转化为直角三角形问题来求解.
G
B

