数学高考中求解范围问题常见错误分析

甘肃省平凉市华亭一中(744000)

蹇桂花 ●



数学高考中求解范围问题常见错误分析

甘肃省平凉市华亭一中(744000)

蹇桂花 ●

赵振威主编的《中学数学教材教法》(第一分册总论)中，对数学的特点归结为三性：抽象性、精确性和应用的广泛性.数学的精确性，指的是数学具有逻辑的严密性和结论的确定性.

而由于数学的精确性的要求，我们在做题时，只要思维上有一丁点疏忽，便会导致结论大相径庭.

近几年高考中，求解参数的范围问题是热点，几乎年年都考，但对学生而言又是难点、易错点，得分偏低.本文就学生在求解范围时，常见的错误加以整理、分析错因，希望对大家有警醒作用.

一、审题粗枝大叶，致误

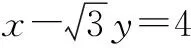
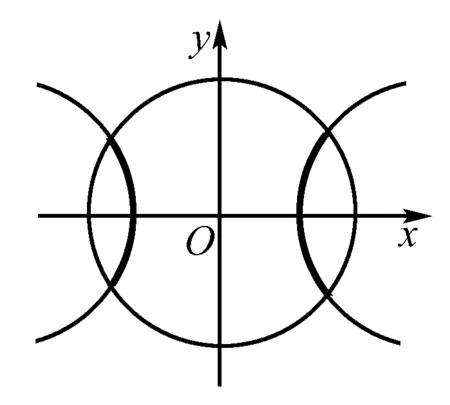
(1)求圆O的方程；

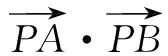
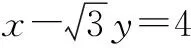
设P(x,y),则有|PO|2=|PA|·|PB|,∴x2-y2=2.

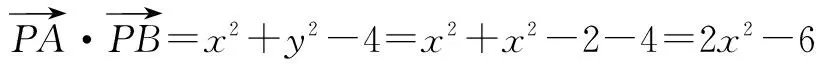
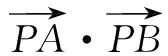
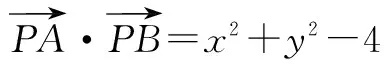
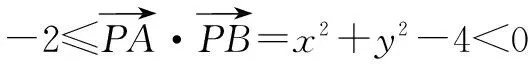
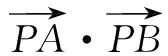
二、未挖掘题目中的隐含条件，致误

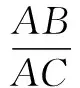
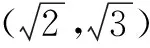
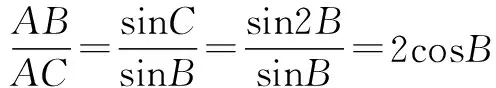
又∵∠C=2∠B且△ABC为锐角三角形,

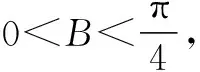
错因 此时选项B、C均符合，应由三角形内角和定理，再求出∠A，保证∠A也为锐角.否则，只由∠B、∠C为锐角，并不能确定△ABC为锐角三角形.

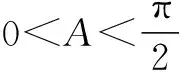
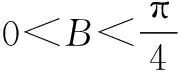
例3 设实数x,y满足2x2-6x+y2=0,求x2+y2+2x的最大值.

错解 ∵2x2-6x+y2=0, ∴y2=-2x2+6x.

令h(x)=x2+y2+2x=-x2+8x.

而函数h(x)的对称轴为x=4,

∴当x=4时，h(x)取得最大值为h(4)=16.

错因 错解只由已知条件将y2作了代换，未考虑题中隐含y2≥0这一条件，导致函数h(x)定义域扩大.

正解 由y2=-2x2+6x≥0得0≤x≤3.对函数h(x)=-x2+8x而言，其定义域为[0,3].

∴h(x)max=h(3)=15.

三、错用不等式性质，扩大范围致误

例4f(x)=ax2-c满足-4≤f(1) ≤-1， -1≤f(2)≤5，求f(3)的取值范围.

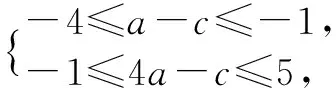
又f(3)=9a-c, ∴-7≤f(3) ≤26.

错因 多次用不等式的不可逆性质，造成范围扩大，而且在求出a、c各自的范围时，破坏了a与c之间原有的关系，把不等式完全当做等式用了，从而导致错误.

正解 此题解法较多，在这只以“待定系数法”为例说明.

∵-4≤f(1) ≤-1，-1≤f(2) ≤5

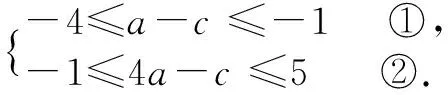
设f(3)=λ1(a-c)+λ2(4a-c),则有9a-c=(λ1+4λ2)a-(λ1+λ2)c,

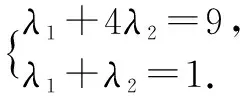
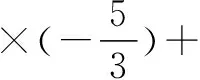
-1≤9a-c≤20,

∴-1≤f(3) ≤20.

四、对概念理解不透，导致范围扩大，致误

错因 只考虑了每段上的情况，未考虑分点处的情况，但题中说是在(-∞,+∞)上为减函数，错误的本质是对减函数概念理解不透彻.

正解 ∵f(x)在(-∞,+∞)上为减函数,

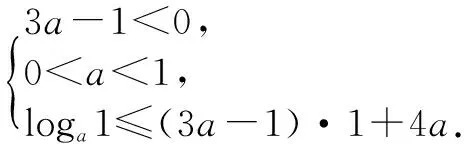
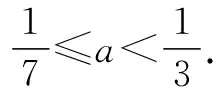
五、未注意定理条件，致误.

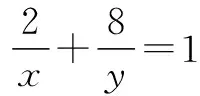
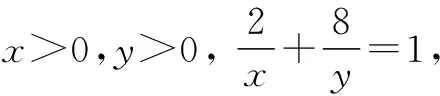
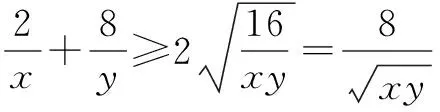
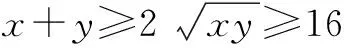
∴(x+y)min=16.

错因 学生在解题时，没有考虑均值不等式中等号成立的条件.(Ⅰ)处取等条件为

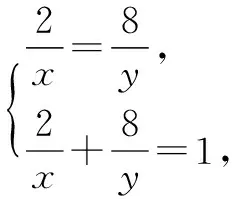
(Ⅱ)处取等条件为x=y，这样两个取等条件矛盾.

∴x+y的最小值不是16.

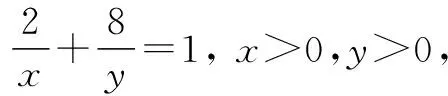
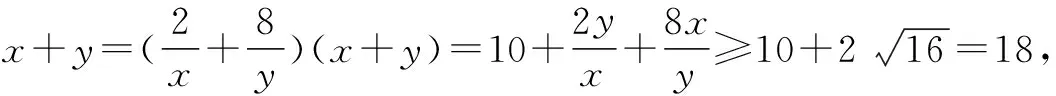
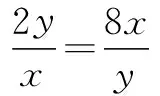
解得x=6，y=12, ∴(x+y)min=18.

求解范围问题虽然是难点﹑热点﹑易错点，但错因要么是审题不仔细﹑不挖掘题意，要么是对知识点理解不深刻，一知半解，模模糊糊，而数学因其精确性和思维的严密性而著称，真正是失之毫厘谬以千里.我们在平时做题时，一定要养成认真审题，对易错﹑易混点及时整理，分析错因，做一个题弄懂这一类题的习惯.这样，无论面对怎样的考试，我们才能得心应手，准确解答.

G632

B

1008-0333(2016)22-0037-02