问诊解三角形问题中的几类高频错解

四川省资阳市外国语实验学校 (641300)

蔡勇全●



问诊解三角形问题中的几类高频错解

四川省资阳市外国语实验学校 (641300)

蔡勇全●

解三角形是高中数学教学中的重点和难点，也是历年高考的必考点和命题热点，但面对利用正余弦定理或三角函数关系所产生的各类解，学生往往缺乏必要的甄别意识和区分技能，从而造成“会而不对，对而不全”的现象时有发生．本文结合实例辨析解三角形问题中的几类高频错解，供大家参考．

一、忽视三角形三内角关系而致错

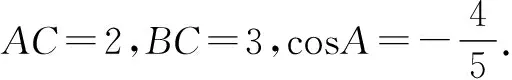
(Ⅰ)求sinB的值；

(Ⅱ)求sin(2B+30°)的值．

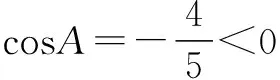
评注 “任意三角形中三内角之和必为180°”是求解所有三角形问题时都应重视的一个隐含条件，也往往是解决此类问题的关键．

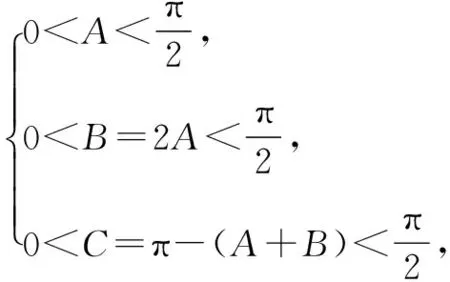
二、忽视三角形角之间的内在制约而致错

例2 在△ABC中，c=4,C=60°，求△ABC周长的最大值．

评注 三角形角之间的内在制约的前提是上文提到的内角和定理，在此基础上，如果已知某一个角，那么余下两角之和必为定值，这就形成了一种制约关系．

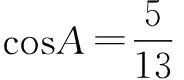
三、忽视对解的个数的判断而致错

辨析 本题的根本错因在于忽视了对三角形解的个数的判断，因为已知两边长与其中一边的对角解三角形可能出现两解、一解、无解三种情况，因此在利用正弦定理解三角形时要根据解的个数进行判断以避免出现错误．

评注 对三角形解的个数的判断往往是建立在使用正余弦定理的基础上，借助边边关系影响角角关系或角角关系影响边边关系来确定解的个数．

四、忽视三边关系定理而致错

例4 已知2a+1，a，2a-1是钝角三角形的三边长度，求a的取值范围．

评注 三边关系定理“任意三角形中，两边之和大于第三边，两边之差小于第三边”是解三角形问题的隐含条件，也是求解本题的关键．

变式 已知锐角三角形的三边长分别为 1、3、a，求a的取值范围．

▶

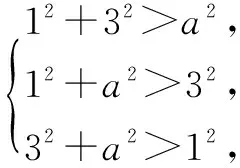
五、忽视三角形的内角范围而致错

例5 在△ABC中，已知sin2A=sin2B，试判断此三角形的形状．

错解 因为sin2A=sin2B，所以2A=2B,A=B，△ABC为等腰三角形．

辨析 上面由“sin2A=sin2B”到“2A=2B”不是等价转化，因未考虑三角形中角的范围而致错．

评注 任意三角形中，正是因为三内角之和等于180°，所以才会有三个内角均介于0°～180°之间这样的隐含信息．

G632

B

1008-0333(2016)22-0021-03