关于一道“基本不等式问题”的解法讨论

新疆巴州库尔勒市石化路华山中学(841000)

马宏云●



关于一道“基本不等式问题”的解法讨论

新疆巴州库尔勒市石化路华山中学(841000)

马宏云●

本文通过对一道“基本不等式问题”解法的探究展现高中数学解题方法的多元性，注重解题通法，拓宽解题思路.

基本不等式；解法；基本不等式法；消元法；换元法

例 已知a,b为实数，且a2-ab+b2=1，求a+b的最大值.

方法一 基本不等式法

点评 此法关注了须知的形式，巧妙地对已知进行了配凑.

方法二 二次使用基本不等式法

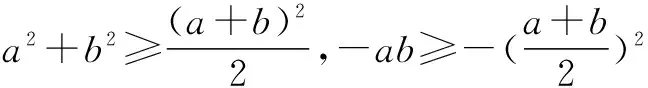
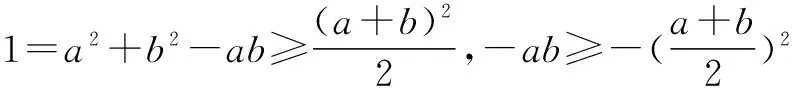
点评 在解题中，一般我们不会使用两次基本不等式，因为取等条件若不同，直接会错解，但是此题中由于“加号”两边的项系数均为1，所以两个基本不等式的取等条件一致，皆为a=b时取“等号”，因此，解法有效.这需要我们在解题中冷静分析，灵活处理.

方法三 消元法

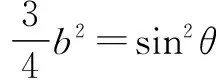
点评 消元法也即函数法，它指将两个有关系的变元的其中一个用另外一个表示出来，来达到将两个变元求最值问题转化为一个变元求最值问题，于是上升到函数问题，考虑到该题有根式，所以想到了三角换元，该题用求导的方法亦可解出.

方法四 消元法(配凑消元)

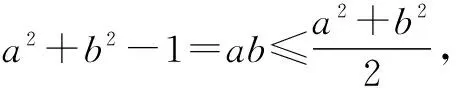
∴(a+b)2=a2+b2+2ab=a2+b2+2(a2+b2-1)=3(a2+b2)-2≤4,

∴-2≤a+b≤2.

点评 此法是将a2+b2整体作为解题的桥梁和纽带，在已知中将ab借助重要不等式消去，再将欲求平方，再次消去ab，来达到解题的目的，这种整体代换的思想在一般解决数学问题中也比较常用.

方法五 换元法(整体代换)

设a+b=t，则b=t-a，于是原式即为a2-a(t-a)+(t-a)2=1，也即3a2-3at+t2-1=0.

∵a∈R，∴方程有解，∴Δ≥0,

∴即9t2-12(t2-1)≥0,∴-2≤t≤2.

点评 此法意为求什么就先设什么，在解题时用的比较多，比如在求函数解析式、求函数的值域、圆锥曲线问题、求复数等多个领域都会使用到，先设出欲求为t，将其看成已知，再借助其它已知构造方程或不等式，最终解决问题.另外，学习三角函数时我们求过sinθ+cosθ+sinθcosθ这个式子的最值，也是利用了换元法，设sinθ+cosθ=t，用t将sinθcosθ表示出来，从而突破了该题.

方法六 换元法(三角换元)

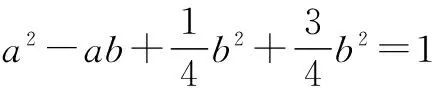
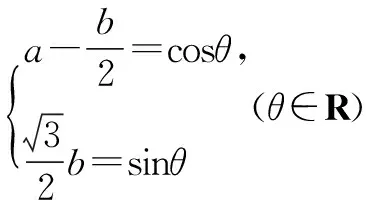
点评 该法难点是对已知进行配凑以便更好地剥离两个字母达到简单换元的目的，不宜普遍学习使用.

下面的几道题都可采取以上六种方法之一进行求解，属一类问题：

1.(2010重庆理7)已知x>0，y>0，x+2y+2xy=8,则x+2y的最小值是____.

2.(2011浙江文16)若实数x,y满足x2+y2+xy=1，则x+y的最大值是____.

3.(2012浙江文9)若正数x,y满足x+3y=5xy，则3x+4y的最小值是____.

4.(2015全国高一数学联赛)已知x,y为实数，且满足2x2+3xy+2y2=1，求x+y+xy的最小值.

总之，基本不等式中的题目解题具有相当大的灵活性，我们只有吃透解法，挖掘形式，注重思维的迁移、发散和联想，大胆尝试，巧妙转化，才可以轻松解决，也才可以使自己在数学的道路上越走越远.

G632

B

1008-0333(2016)22-0041-01