构造向量解(证)高考题

广东省东莞市沙田广荣中学(523991)

何勇波 ●



构造向量解(证)高考题

广东省东莞市沙田广荣中学(523991)

何勇波 ●

近年来一些高考题如果用常规方法解答，计算量很大，而且容易算错，如果通过构造向量，用向量的方法解答或证明，将可以大大减少计算量，增加解题的准确程度.

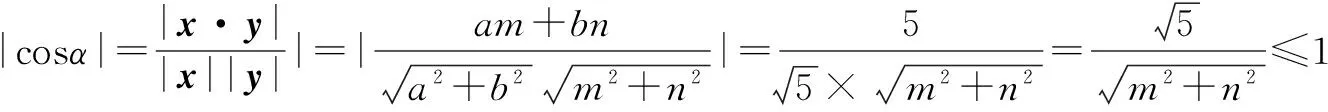
例2 (2014年北京高考文科题)已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0)，B(m,0)(m>0)，若圆C上存在点P，使得∠APB=90°，则m的最大值为( ).

A.7 B.6 C.5 D. 4

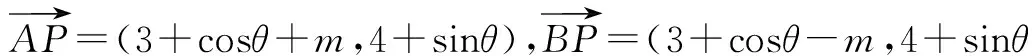
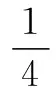
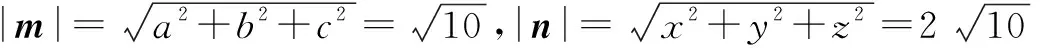
例4 (2013年湖南高考理科题)已知a,b,c∈R，a+2b+3b=6，则a2+4b2+9c2的最小值是____.

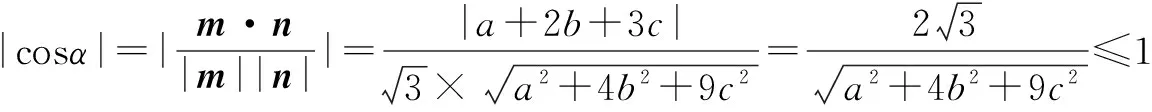
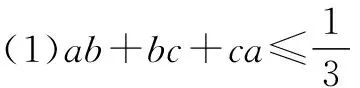
证明 (1)略.

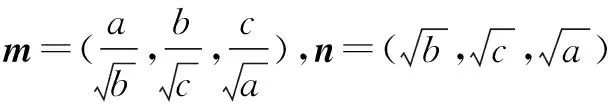
例6 (2014年高考福建理科建卷)已知定义在R上的函数f(x)=|x+1|+|x-2|的最小值为a.(Ⅰ)求a的值；(Ⅱ)若p,q,r为正实数，且p+q+r=a，求证：p2+q2+r2≥3.

证明 (1)amin=3(解题过程略).

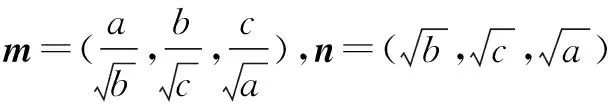
G632

B

1008-0333(2016)22-0010-01