300 MN薄板成型压机框架有限元分析及结构优化
陈惠娟,姜 峰,李吉萍
(兰州兰石能源装备工程研究院有限公司,甘肃 兰州 730314)
300 MN薄板成型压机框架有限元分析及结构优化
陈惠娟,姜 峰,李吉萍
(兰州兰石能源装备工程研究院有限公司,甘肃 兰州 730314)
采用有限元方法对300 MN多缸薄板成型压机框架进行了应力分析,查看应力集中情况,并对容易产生应力集中的初始圆角进行局部优化,得出圆角最优变量值。再结合各种常见的过渡圆角结构,赋予变量参数,进行局部集中应力优化,找出最优过渡圆角结构,以改善压机框架应力集中的情况。
压机框架;液压机;应力分析;圆角优化
薄板是板式换热器的主要组成部分之一,其压制精度要求较高,传统的薄板成型液压机由于自身工作台的变形量大,并且随着液压机吨位的提高,工作台变形量增大,导致作用于模具上的载荷不均匀,不能满足实际生产中的精度要求。近期我公司自主研发的300 MN多缸薄板成型液压机(以下简称压机),近乎均布的多个油缸同时作用工作台成型,降低了工作台自身受力不均导致的变形,使得模具受力更加均匀,压制的薄板成型产品质量稳定、精度高。
机架是压机的主体,设计的合理与否直接关系到压机的整体强度及工作精度,国内不少学者在机架这方面进行了探索分析[1-6],由于我们所研究的压机在国内尚属空白,没有查阅到相关机组的研究报导,在不清楚框架应力集中规律的情况下,盲目增加材料,不仅会增加成本,而且未必达到效果。
针对上述情况,以压机框架为研究对象,运用有限元分析法对其在极限工作载荷状态下进行分析,得到框架任意位置的应力分布状态,为进一步对框架优化结构布局提供依据。
1 有限元分析
1.1 有限元模型的建立
该压机机架为框架式,框架是由多片等尺寸的O形板叠加,通过拉杆连接组成的,O形板为整块钢板切去中间区域的整板,可以将其看作由上横梁、立柱、下横梁三部分组成,压机框架结构如图1所示。
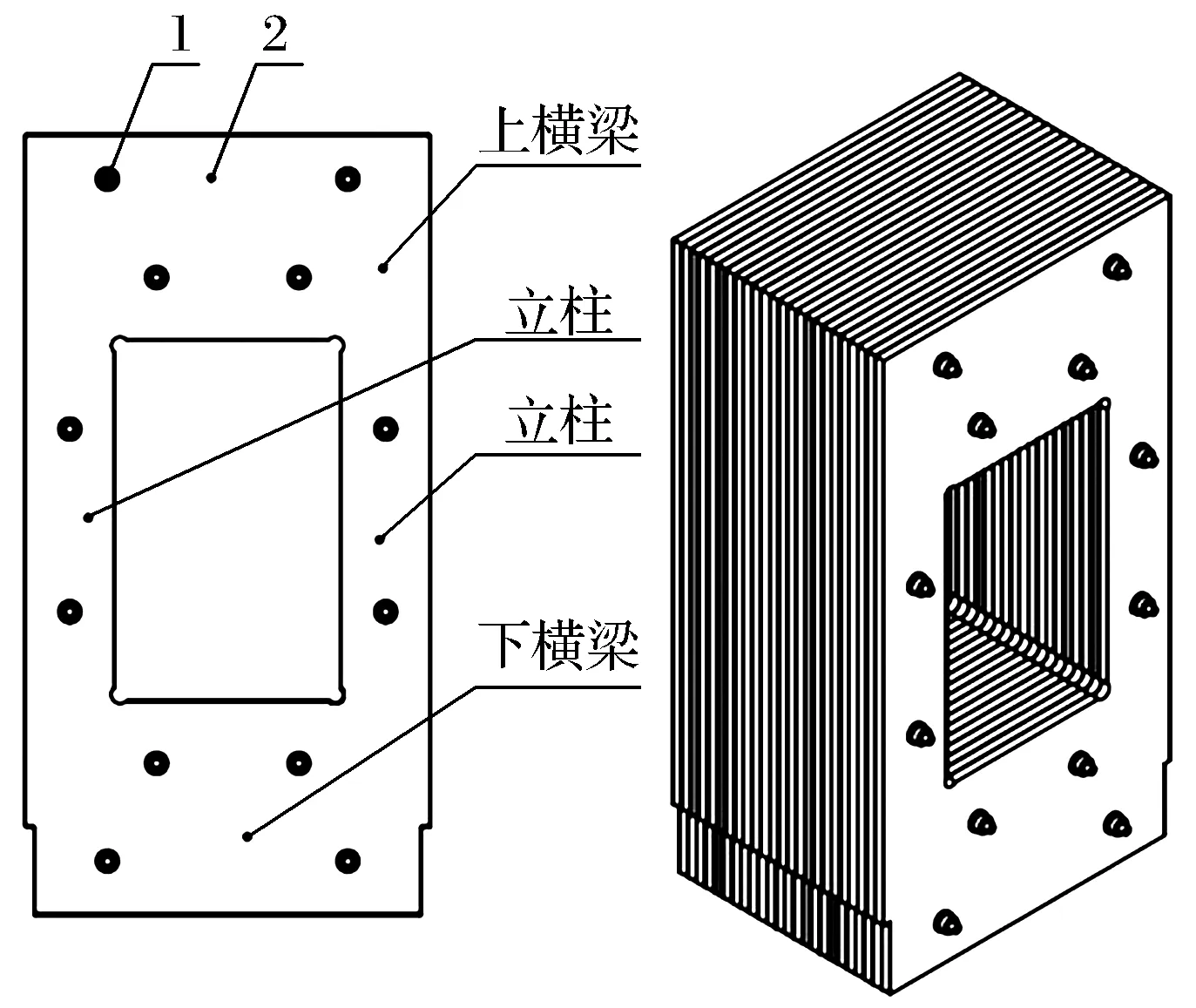
1.拉杆组件; 2.O形板图1 压机框架结构示意图Fig.1 Press frame structure diagram
采用三维建模软件Solidworks建立O形板的几何模型,造型时对不影响整体强度刚度的一些细节结构进行简化,然后将建好的模型导入到ANSYS workbench软件中进行网格划分。全部采用六面体单元对模型进行自由网格划分,并对圆角过渡区域进行细化,网格质量优秀,单元类型选取为实体Solid186号单元。
1.2 边界条件加载
压机在一个工作周期内有加载、保压和卸载三个工作状态,分析不考虑动态载荷的影响,仅对压机框架在保压状态下进行静态强度分析。
压机工作时,多个加载油缸的压力通过工作台、被压板材及模具等作用于上横梁,下横梁连接板承受着底座对油缸的支撑反力,框架受力可看作是对称负荷。油缸分布状态可近似为均布,为了简化问题,将框架上、下作用力区域的载荷近似等效为均布面载荷,忽略底座、模具、工作台及被压板材等的重量。由于框架区域受均匀载荷,分析框架的应力情况与单个O形板的应力情况近似,研究以一个O形板为分析对象,求解其在极限载荷下的应力情况,以了解整个框架的应力分布。
压机输出最大总载荷为300 MN,共有24个O形板,平均每个板受力为12.5 MN,为对称载荷,对其加载两个大小相等、方向相反的力。根据压机实际运行情况,框架通过基础梁固定在基础之上,将O形板凸边下底面与基础梁接触部分定义为全约束,侧面与基础梁接触部分约束、自由度等O形板结构简图及有限元分析模型如图2所示。O形板材料为Q345B,材料弹性模量为206 GPa,泊松比为0.3,密度为7.85×103kg/m3,屈服强度为345 MPa。

1.全约束; 2.约束x、z两个自由度图2 O形板结构简图及有限元分析模型Fig.2 O shaped plate structure diagram and finite element analytical model
1.3 结果分析
通过对压机框架的有限元分析,得出其最大工况载荷下的等效应力分布,如图3所示。分析结果表明,机架的受力不均匀,存在较为严重的应力集中现象,立柱及上横梁上部、中间部分应力值较大,对应的集中应力分别为191.1 MPa、169.9 MPa,机架材料为Q345B,其屈服强度为345 MPa,设计要求安全系数为2.2,其许用应力为156.8 MPa,应力集中区域的最大应力值均已超过许用应力。

图3 等效应力云图(0~191 MPa)Fig.3 Equivalent stress nephogram (0~191 MPa)
将上圆角处的应力云图局部放大,见图4,从图4中可以看出,圆角的最大应力点位于立柱端的过渡圆弧处,该模型在过渡圆角处存在应力集中。

图4 圆角区域等效应力云图(0~191 MPa)Fig.4 Equivalent stress nephogram in circular bead area (0~191 MPa)
在实际使用中,压机整个框架长时间承受几万吨的载荷作用,框架上横梁与立柱的过渡区域、下横梁与立柱的过渡区域是其强度最弱区域,该区域承受上横梁、下横梁对立柱的拉伸应力和弯曲应力,是框架受力最大区域,也是应力集中系数最大区域[7]。该应力主要由框架立柱侧向变形及上、下横梁弯曲变形引起,为拉应力和弯曲应力的合成,该应力也为工作应力,可通过优化圆角结构参数,减小材料的集中应力系数,确保应力在材料的许用范围之内。
2 过渡圆角结构参数优化
在初始模型有限元分析的基础上,对初始模型的圆角部分参数化并进一步优化。O形板过渡处的初始圆角结构如图5所示,圆角为1个过渡圆弧槽,圆弧槽的半径为R0,圆弧的圆心到上横梁底面的距离为H0,到立柱侧面的距离为M0。
优化的设计变量为
X=[R0,H0,M0],
其中:R0∈[100,200];H0∈[5,100];M0∈[5,100]。

图5 圆角结构示意图Fig.5 Circular bead structure diagram
目标函数选择圆角区域的最大等效应力,优化方法选择ANSYS workbench中的直接优化方法。通过优化,得出该过渡圆角优化后的最大应力值为174.4 MPa。
在压机框架初始刚度下,O形板的过渡圆角优化后,与初始模型的分析结果相比,圆角区域的最高应力值减小了16.67 MPa,但仍大于材料的许用应力,说明该过渡圆角结构不适于实际工况要求,有必要对该结构进行改进。
通过改进初始模型的过渡圆角结构,并对改进后的圆角结构进行参数优化,找出最优结构参数变量值。常见的圆角结构如图6所示[3,8]。
根据以上优化分析结果,将初始模型不合理的过渡圆角结构分别更换为图6中的7种圆角结构形式,保持初始模型刚度及施加的极限载荷大小不变,采用上述局部优化分析的方法,将各圆角结构参数化,设置对应的变量范围,以圆角区域的最大应力值作为目标函数,求出各结构下的最优目标函数值。对比分析结果,选出较理想的过渡圆角结构。

图6 常见过渡圆角结构Fig.6 Common transition circular bead structure
各结构的变量定义范围、优化后的最优变量值及对应的最优目标如表1所列。

表1 各结构优化结果及对比
通过表1可以看出结构e、f、g为较好的过渡圆角结构,其中结构e椭圆圆弧是以上提及的所有常用圆角结构中最好的过渡结构,最高应力值降至材料许用应力范围内。
3 结论
通过以上分析与优化可以得出以下结论:
(1) 通过对初始模型应力分析可得,初始圆角结构并不合理,存在较为严重的应力集中,并且最高应力为191.1 MPa,超过材料的许用应力。
(2) 通过对初始模型圆角结构参数的优化,得出初始模型的最优结构,最高应力得到一定程度的下降,但优化之后圆角区域的最高应力仍大于材料的许用应力,说明初始模型的圆角结构不合理。
(3) 将初始模型的圆角结构更换成不同的圆角结构并进行参数化优化,结果表明1/4椭圆弧(结构e)是最优圆角结构。该圆角结构基本不存在集中应力的情况,圆角区域的最大应力为85.59 MPa,相比于初始结构的最大应力其下降了55%。
[1] 高翔,胡淼.框式热压机机架有限元分析及结构优化设计[J].机械设计,2009,26(4):62-64.
[2] 张新洲,蒋清海,武凯,等.压机框架有限元分析及试验验证[J].机械科学与技术,2012,29(3):11-15.
[3] 李刚.热压机框架板的受力分析及改进措施[J].木材加工机械,2003,14(5):8-11.
[4] 张汝,刘为,张倩倩,等.压力机机架设计的有限元分析[J].精密成形工程,2011,3(2):39-42.
[5] 刘强,付文智,李明哲,等.三梁四柱式多点成形压力机机架结构有限元分析和优化设计[J].塑性工程学报,2003,10(5):49-52.
[6] 刘兴,李永堂,闫红红,等.80 MN双柱斜置式快锻液压机机架有限元分析[J].锻压装备与制造技术,2012,47(4):16-18.
[7] 吴新泉.人造板多层热压机[M].北京:中国林业出版社,1985.
[8] 王尚斌,孙宇,武凯.压机框架有限元分析及结构优化[J].机械设计,2011,28(4):79-85.
300 MN Sheet Moulding Press Frame Finite Element Analysis and Structure Optimization
Chen Huijuan,Jiang Feng,Li Jiping
(LanzhouLsEnergyEquipmentEngineeringInstituteCo.,Ltd.,Lanzhou730314,China)
Analyze the stress of 300 MN multi-cylinders sheet moulding press frame by finite element method and observe the situation of centralized stress;optimize the part of initial circular bead which easily makes stress centralized,as last,the optimized variable value of circular bead is concluded.Furthermore,with every kind of common transition corner structure,we give variable parameter to optimize centralized stress in part and find out the best transition corner structure,reaching the aim of improving the situation that stress is centralized.
Press frame;Hydraulic machine;Stress analysis;Circular bead optimization
Chen Huijuan,Jiang Feng,Li Jiping.300 MN Sheet Moulding Press Frame Finite Element Analysis and Structure Optimization[J].Journal of Gansu Sciences,2016,28(6):65-68.[陈惠娟,姜峰,李吉萍.300 MN薄板成型压机框架有限元分析及结构优化[J].甘肃科学学报,2016,28(6):65-68.]
10.16468/j.cnki.issn1004-0366.2016.06.013.
2015-06-04;
2015-07-21.
甘肃省科技重大专项(143GKDA014).
陈惠娟(1985-),女,福建诏安人,硕士,工程师,研究方向为锻压机械的研发设计.E-mail:juanhuichen@163.com.
TG315.4;TH123+.4
A
1004-0366(2016)06-0065-04

