油气管道流固耦合振动特性数值分析*

徐 凯，张 峰，李周波，白 鹤，鲁碧为，马佼佼

（1.国家石油天然气管材工程技术研究中心，陕西 宝鸡721008；2.宝鸡石油钢管有限责任公司 钢管研究院，陕西 宝鸡721008）

油气管道流固耦合振动特性数值分析*

徐 凯1,2，张 峰1,2，李周波1,2，白 鹤1,2，鲁碧为1,2，马佼佼1,2

（1.国家石油天然气管材工程技术研究中心，陕西 宝鸡721008；2.宝鸡石油钢管有限责任公司 钢管研究院，陕西 宝鸡721008）

油气管道服役时由于内部输送油气会产生压力，使其运行的动态环境发生质变，导致管体结构与内部流体产生耦合等一系列问题。为了减小这些问题有可能对整个管道系统造成的重大危害，以某型油气管道为研究对象，建立了管道流固耦合系统的有限元分析模型，分别对管道的结构、内腔流场及其流固耦合系统的模态进行研究；针对其所处的特殊动态环境，考虑流固耦合效应，进行仿真分析，考察管道耦合系统的整体服役特点。计算结果表明，管道结构的在其低阶模态处表现了较为整体的振型，而在较高的频段内则显示出了大量的局部模态；管道内腔流场的模态振型呈对称分布，耦合系统模态的大部分振型与管体结构较为类似。

油气管道；流固耦合；有限元法；振动特性

近年来，随着国内外经济的飞速发展，各国对于石油、天然气等基础能源的需求也大幅增加。油气管道是石油天然气的主要运输方式，在石油工业甚至整个经济体系中都占有举足轻重的地位。然而，随着管道输送量的不断加大，管径、壁厚及强度等不断提升，许多被忽略的问题都会显现出来，如内部输送流体的振动对管道结构服役性能的影响等。这些问题对管道的结构设计、制造都提出了更高要求[1]。

在许多实际的工程研究领域，工程结构和其他相关的学科间日益交叉，其中包括压力、位移、温度场等物理量之间的相互耦合。分析计算的结构也往往不是一个单独的物理场，而是处于多个物理场相互耦合中，越来越多的问题需要进行耦合场分析[2-4]。

对于油气管道的研究，传统的大量研究只是单一地分别集中于管道的结构特性或者管道内部的流体动力学分析。而在实际工程中，油气管道是处在一个大型的流固耦合系统当中，管道的振动会引起内腔流体的非定常流动，产生水锤等现象；反过来，内腔流体的流动又会导致管体的结构振动等[5-6]。因此，基于流固耦合理论的油气管道振动研究十分必要。

振动经典理论已有很长的历史，结构流固耦合特性也已受到许多研究者关注，并且取得了很大进展。由于试验及检测条件等的限制，数值分析由于其快速省时等优点在流固耦合问题中已成为了重要的科研手段，而其中有限元法又是其中最为重要和常用的手段[7-11]。20世纪60年代利用传递矩阵法开创了有限元法在管道流固耦合领域应用的先例，国内外学者也开始对流固耦合系统进行了较为深入的探究，使得有限元法广泛适用于此类问题的求解。

本研究以某油气管道为研究对象，基于有限元法，建立了管道流固耦合系统的有限元分析模型，分别研究了管体的结构模态、内腔流场模态以及考虑流固耦合效应下的系统模态；针对其所处的特殊动态环境，进行仿真分析，考察了管道系统的整体服役振动特点，为管道的结构设计提供参考。

1 流固耦合基本理论

1.1 基本方程

可将管道内腔流场视为一种振动状态的传播，与其内部介质（天然气、石油）相联系[12]。满足物理学运动方程，即牛顿第二定律、质量守恒定律和物态方程，即

式中：p—内部压力；

ρ—介质密度；

v—质点振动速度；

t—时间；

ρ′—密度的增量；

根据介质及传播的基本假设可建立波动方程

1.2 流固耦合有限元方程

对于管道流固耦合系统，考虑内腔结构的刚性壁面、吸声壁面及弹性壁面及其各种边界条件，可以得到内腔体流场的等效积分弱形式[13-14]

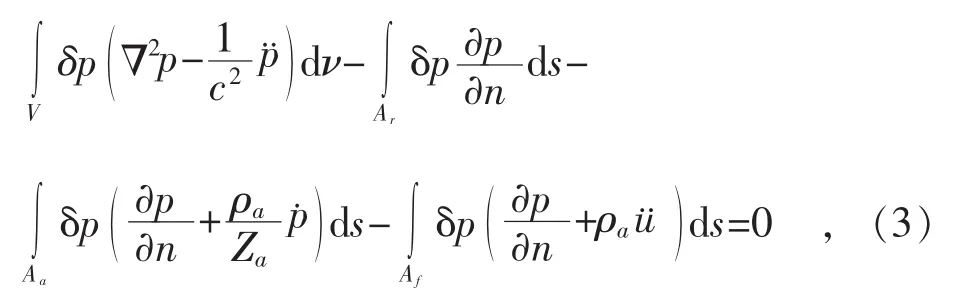
式中：s—管道内部面积；

n—壁面外法线方向；

Za—吸声壁面声阻抗率；

ü—质点振动加速度沿壁面法向的分量；

ρa—流体介质密度；

ν—管道内空腔域；

Ar—刚性壁面域；

Aa—吸声壁面域；

Af—弹性壁面域；

δp—压力的变分。

经过插值可得到与结构耦合的流场有限元方程

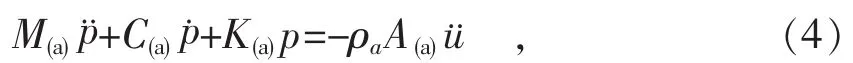
式中：M(a)—流场总体质量阵；

C(a)—流场总体阻尼阵；

K(a)—流场总体刚度阵；

A(a)—流场与结构的耦合阵。

弹性体结构的振动将与内腔流场产生流固耦合作用，根据力学基本方程，可得到结构的等效积分弱形式

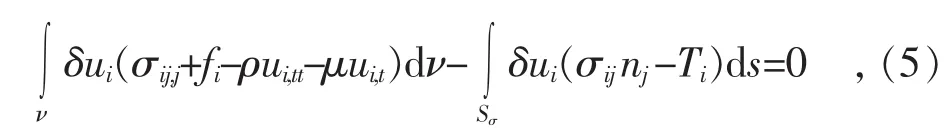
式中： ui（x,y,z）—t时刻的位移场；

nj—边界 sσ的外法线；

σij—二阶应力张量；

Ti—面力。

将内腔声压及其它载荷作为管体结构的载荷，可推导出与内腔流场耦合的结构动力学方程

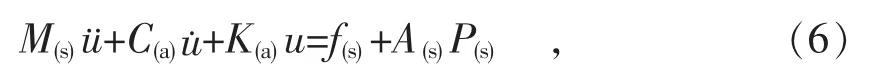
式中：M(s)—结构单元质量阵；

C(s)—结构单元阻尼阵；

K(s)—结构单元刚度阵；

f(s)—结构单元载荷；

A(s)—结构与流场的耦合阵。

在解决结构－流场耦合问题时，同时考虑与流场耦合的结构动力学方程（6）和与结构耦合的流场有限元方程（4）。以结构质点的位移u和流场空间位置声压p为未知量，可得出结构－流场耦合系统的动力学有限元方程

2 数值分析

2.1 有限元模型

以实际工程中的某型油气管道为研究对象，考察其流固耦合特性。首先建立了管体结构、内腔流场及其考虑流固耦合效应下的系统有限元网格模型，如图1所示。

图1 管道结构、内部流场及其结构－流场耦合系统有限元模型

模型网格划分好后，必须在结构与流场空腔之间设置流－固耦合单元（即“接触型”流体单元），该耦合单元是在结构-流场相互耦合的界面上建立的。流－固耦合单元是将结构与流场链接在一起的单元，是结构到流场的过渡[15]。将流－固耦合界面定义成特殊的FSI，如图2所示，只有这样才能在后续的计算中保证结构－流场相互耦合计算的准确性。

图2 流－固耦合界面（FSI）的定义

管道材料为普通碳钢，管道内部空腔介质为天然气，有限元模型所需的材料参数见表1。在0℃及1个大气压条件下，声速为418.96 m/s。对有限元模型网格的划分总共使用了3种单元类型，即管道结构采用四节点等参薄壳单元（Shell 63），管道内腔流场单元分别采用接触型和非接触型的三维流体单元（Fluid 30），单元划分见表2。

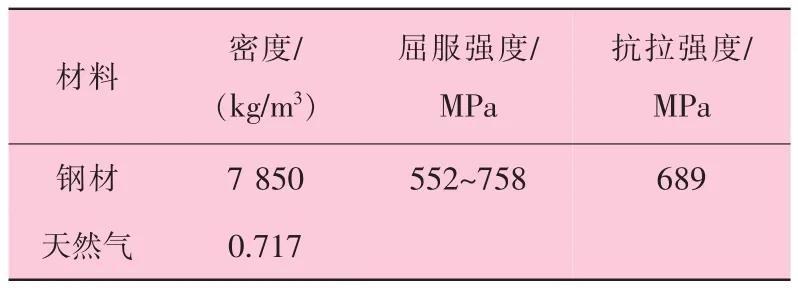
表1 有限元模型所需的材料参数

表2 有限元模型的单元划分

2.2 管道流－固耦合模态分析

2.2.1 管道结构模态分析

结构的固有振动是分析管道振动特性的依据。结合实际工程应用中管道的运行特点，施加两端固支的约束条件，计算了该型油气管道前30阶的结构固有模态。具有代表性的部分模态振型如图3所示。

图3 管道结构模态振型图

由图3可以看出，管道结构的第一阶模态（371.56 Hz）振型表现为整体振动，从第7阶模态（1 684.6 Hz）开始，振型逐步转变为局部模态，且随着频率不断提高，局部模态增多，管道振动逐渐增强。管道结构的在其低阶模态处表现了较为整体的振型，而在较高的频段内则显示出了大量的局部模态。

2.2.2 内空腔流场模态分析

对于管道内空腔流场模态进行分析可用于确定在何处能否激起钢管的共振，以致对结构本身的损伤，可为管道的结构设计提供依据。本研究计算了前30阶管道内空腔流场自由模态。具有代表性的模态振型如图4所示。

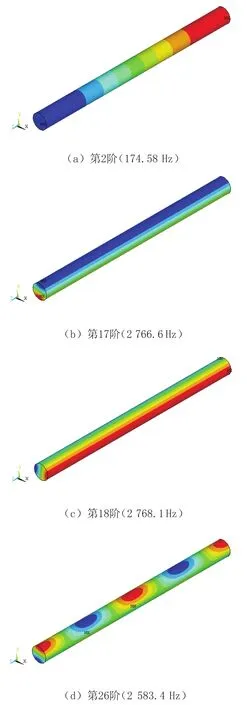
图4 管道内空腔流场模态振型图

空腔内流场的频率和模态振型由其几何形状确定，管道结构为轴对称对称，因此内空腔流场的模态振型也是对称的。由图4可知，前16阶均为流场的纵向模态，内部压力沿纵向变化；第17阶（2 766.6 Hz）开始出现竖向模态，管道底部压力较大；第18阶（2 768.1 Hz）开始出现横向模态，管道侧部压力较大，其余后续的模态均为这三种形式的叠加。

当管道结构的固有模态与内空腔的流体模态重叠时，内空腔与管道结构将发生共振现象，对管道结构本身产生不利影响，如断裂、脆断等。因此在结构设计时应避免此类情况的发生。

2.2.3 结构－内流场耦合系统模态分析

管道结构受外力引起结构振动，结构振动会引起内腔流体介质（空气）的扰动，改变内部流场的流态；同样地，内腔流场所产生的压力同样会影响管体结构的振动，还有可能在某些特定频率处产生共振。因此，将管道结构与内空腔流场耦合起来考虑结构-流场耦合系统的动力学特性是十分必要。本文将结构与内腔流场设定为特殊的耦合界面（FSI），计算耦合系统前30阶模态。耦合系统典型的模态振型如图5所示。

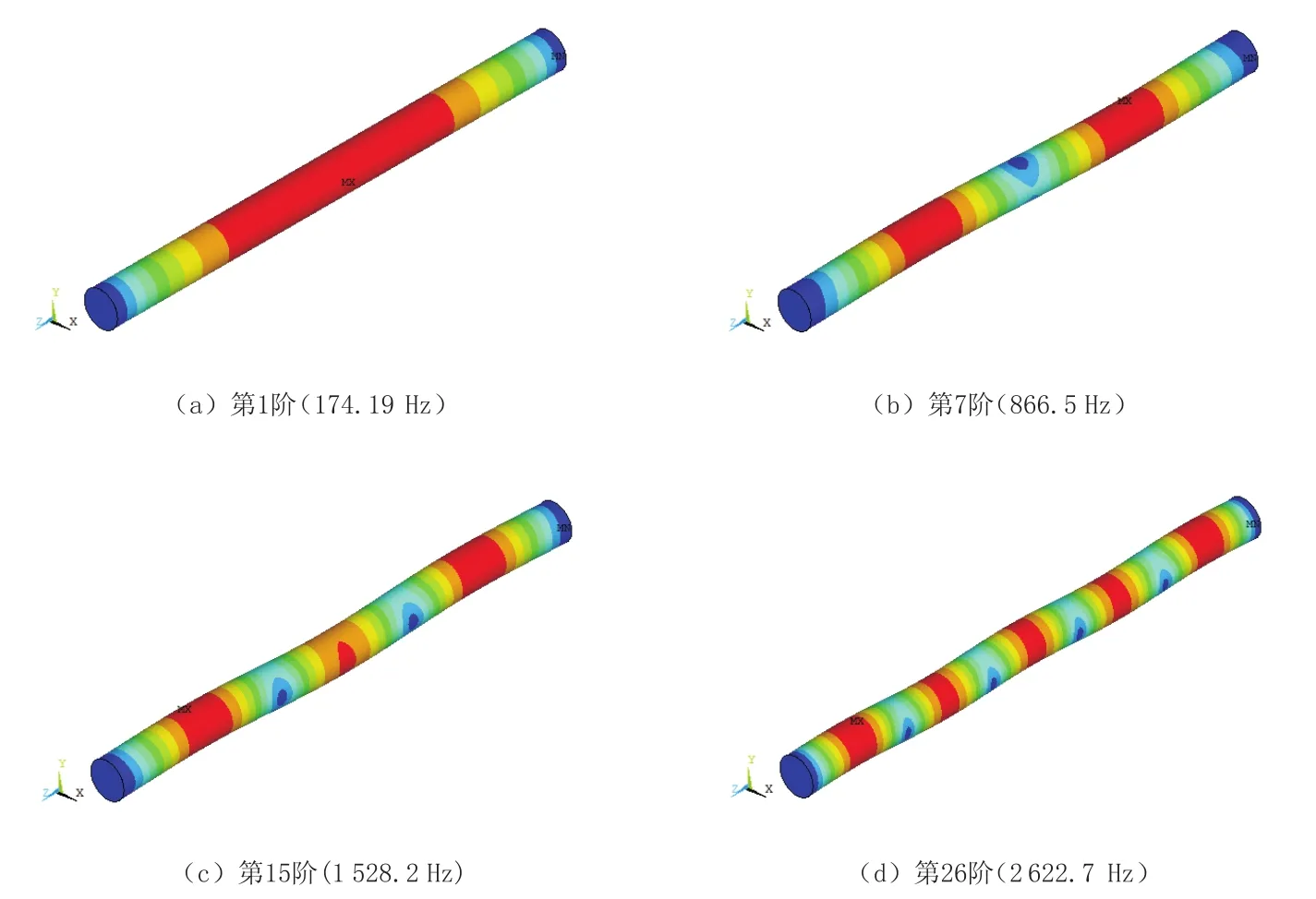
图5 结构－流场耦合系统模态振型图

由图5可见，考虑流固耦合效应后的系统模态与管体结构的振型相近似。大部分表现为管体结构模态，即耦合系统的大部分模态振型与管体结构模态相对应。结构-流场耦合系统模态从第7阶（866.51 Hz）开始逐步变为局部模态。

分别对比前30阶的管体结构、内腔流场以及流固耦合系统的模态频率，对比结果如图6所示。从图6可以看到，三种模态频率均逐步增长，结构-流场耦合效应后的系统模态整体较小；其中管体结构在低阶模态增长较为缓慢，在高阶模态增长较为迅速；内腔流场模态在低阶呈线性增长，在较高阶模态则比较平稳；耦合系统的频率则始终平稳增长且低于结构和流体本身。在第14、15、23、24、25阶结构和内腔流场会产生共振频率，因此在实际工程中要特别重视。

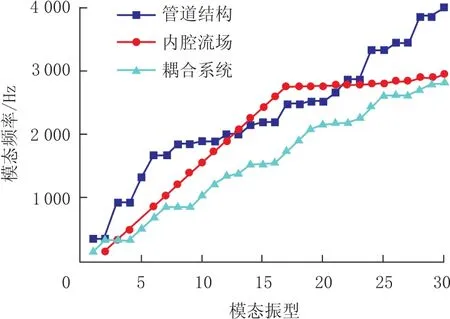
图6 模态振型频率对比

3 结 论

（1）三种模态频率都是逐步增长的，考虑结构－流场耦合效应后的系统模态整体较小。

（2）管道结构在其低阶模态处表现了较为整体的振型，而在较高的频段内则显示出了大量的局部模态；内腔流场的各阶模态振型左右对称，高阶模态为纵向、竖向、横向以及三种形式的复合叠加，耦合系统模态大部分表现为管体的结构模态，与其振型亦相类似。

（3）在某些特定频率处，流场模态与结构模态振动频率很接近，这将会产生共振致使管道振动加剧，使其运行状态产生危险等。

[1]李琳，喻立凡.管道及管路系统流固耦合振动问题的研究动态[J].应用力学学报，1997，14（3）：40-47.

[2]刑景棠，周盛，崔尔杰.流固耦合力学概述[J].力学进展，1997（1）：19-38.

[3]钱若军，董石麟，袁行飞.流固耦合理论研究进展[J].空间结构，2008，14（1）：1-9.

[4]苏波，钱若军，袁行飞.流固耦合界面信息传递理论和方法研究进展[J].空间结构，2010，16（1）：3-9.

[5]张立翔，黄文虎.输流管道流固耦合振动研究进展[J].水动力学研究进展，2000，15（3）:366-379.

[6]任建亭，姜节胜.输流管道系统振动研究进展[J].力学进展，2001，33（3）:313-324.

[7]APPA K.Finite Surface Splines[J].Journal of Aircraft，1989，26（5）：495-496.

[8]SMITH M J，HODGES D H.Evaluation of Computational Algorithms Suitable for Fluid-structure Interactions[J].Journal of Aircraft，2000，37（2）：282-288.

[9]SAMAREH J A.Discrete Data Transfer Technique for Fluid-Structure Interaction[C]//18th AIAA Computational Fluid Dynamics Conference，2007，AIAA Paper：2007-4309.

[10]GLUCK M，BREUCR M，DURST F，et al.Computation of fluid-structure interaction on lightweight structures[J].Journal of Wind Engineering and Industrial Aerodynamics，2001，89（14-15）：1351-1368.

[11]KRUNTCHEVA M R.Acoustic-structural resonances of thin-walled structure-gas systems[J].Journal of Vibration＆Acoustics,2006,128（6）：722-731.

[12]盛美萍，王敏庆，孙进才.噪声与振动控制技术基础[M].北京：科学出版社，2007：33-36.

[13]孙淦云.声-结构耦合系统振动分析和灵敏度分析[D].大连：大连理工大学，2003.

[14]丁渭平，陈花玲.腔体声振耦合的对称化有限元模型及其特性研究[J].西安交通大学学报，2000，34（7）：58-62.

[15]宋学官，蔡林，张华.ANSYS流固耦合分析与工程实例[M].北京：中国水利水电出版社，2012：1-2.

Numerical Analysis of Fluid-solid Coupling Response for Oil and Gas Pipeline

XU Kai1,2，ZHANG Feng1,2，LI Zhoubo1,2，BAI He1,2，LU Biwei1,2，MA Jiaojiao1,2
（1.Chinese National Engineering Research Center for Petroleum and Natural Gas Tubular Goods，Baoji 721008，Shaanxi，China；2.Steel Pipe Research Institute，Baoji Petroleum Steel Pipe Co.,Ltd.,Baoji 721008，Shaanxi，China）

When the oil and gas pipeline in service,the transporting oil and gas will produce pressure,it makes the operational dynamic environment occur qualitative change,which leads to a series of problems,such as coupling between pipeline structure and interior fluids.The above problems are likely to cause significant harm to the whole pipeline system.A FE model of fluid-solid coupling analysis for some type oil and gas pipeline was set up to study the pipeline structure,the fluid modes and the coupling modes.According to the special dynamic environment,considering fluid-solid coupling effect,the simulation analysis was carried out,and the whole service characteristics of pipe coupling system were inspected.The results showed that the structural modes appear a good wholeness at lower frequencies,and appear most local modes at higher frequencies.The fluid modes appear some symmetries.The most modes of coupling modes are more similar to pipeline structure.

oil and gas pipeline；fluid-solid coupling；FEM；vibration characteristics

TE832 文献标志码：B DOI:10.19291/j.cnki.1001-3938.2016.03.006

油气管道工程建设新技术、新产品研究“高钢级ERW油井管新技术研发”（项目号2009A-3006）。

徐 凯（1987—），男，硕士研究生，助理工程师，主要从事油气管材开发与技术研究工作。

2015-08-06

黄蔚莉