基于遗传算法的汽车零配件仓库货位优化研究

侯忠，郑国华

(中南大学 交通运输工程学院，湖南 长沙 410075)



基于遗传算法的汽车零配件仓库货位优化研究

侯忠，郑国华

(中南大学 交通运输工程学院，湖南 长沙 410075)

仓库货位优化问题是仓储管理的重要内容之一。针对配件库汽配货物种类繁多、出入库频率差异较大、需求时间与需求数量具有随机性等特点，对配件库汽配件货物的货位分配与优化问题进行讨论，在明确库内配件货物货位优化思路的基础上，建立基于货位优化的多目标规划模型。最后将此多目标规划模型转化成单目标规划模型，并设计求解此模型的遗传算法。实例结果表明：采用此优化策略能够有效地解决汽配件货物的货位优化分配问题。

仓储管理；货位优化；遗传算法；汽车配件

仓储是物流系统的一个重要组成部分。据估算，储存和物料搬运成本占物流总成本的26%，因此加强仓储管理，提高仓储运作效率，降低仓储运作成本是降低物流成本的重要途径。汽车配件仓储是一种特殊的仓储类别，配件库汽配货物具有种类繁多、出入库频率差异较大、需求时间与需求数量具有随机性等特点。汽车配件仓储作为汽车行业售后物流的一个重要环节，在整个供应链中也扮演了非常重要的角色[1]。

货位优化是仓库布局研究的一个主要分支，随着现代计算机技术以及控制技术的不断发展，生产企业和物流仓储企业仓库管理呈现出控制最优化、运行智能化的发展趋势，对仓库的货位优化已成为物流技术发展的一个重要标志[2]。国外对仓储货位优化研究相对较早。Hesket[3]研究了货物存储所需要的存储空间以及货物的订单数量对仓储效率的影响。Goetschalckx等[4]证明了N类货物分配下最低COI值的货物存储在最适宜的货位，订单拣选和存储时间得到了优化。Graves等[5]分析了货物组合成更少的类别时，高周转率的货物可能会占据不理想的货位。Rosenwein[6]提出了货位布局的分级存储策略。Larson等[7]在Rosenwein研究基础上，使用启发式算法对分级存储策略进行探讨。Sooksaksun等[8]基于分类存储策略对巷道的数量、长度、产品的分类存储建立数学模型，模型以最小化平均行走距离为目标。Zhan等[9]研究了带邻接约束的多层次仓库布局问题，建立了描述同类产品的临近放置的整数规划模型，并采用禁忌搜索算法求解。

在国内，对货位优化研究方面，文献[10]和[11]为本文在算法方面的探究提供了算法的支持,认为遗传算法在解决货位优化NP-难问题方面具有有效性。谭泽波[12]以货物的位置、货物的质量和存取次数为变量建立货位优化模型，文章对货物的相关性等因素缺乏考虑。董溪哲等[13]提出了以物品周转率为标准的货位优化模型。王建[14]以货物出入库效率、货架稳定性以及货品存放的相关性为目标建立了多目标的优化模型，采用权重系数法将多目标问题转化为单目标问题，但没有对不同量纲的目标函数做标准化处理。吴璟等[15]重点讨论了影响拣货效率的因素，根据这些因素引入拣货成本系数，在路径、周转率等关键指标基础上建立线性规划的货位模型。郑凌莺[16]在解决货物相关性即产品族的问题方面，综合考虑货物的周转率、重量和类聚现象的三个主次目标，建立货位优化的多目标模型。马永杰等[17]基于随机存储策略对自动化仓库的库区和货位分配以及堆垛机行驶时间进行优化，在约束条件中考虑到堆垛机容量和速度。马婷[18]提出基于最小时间算法的货位优化方法，建立自动化立体仓库三维立体模型，实现了对烟草仓库货位的优化。

应当看到的是，上述研究成果大多仅局限于理论探索层面，由于每个仓储企业的业务范围、服务对象的差异，特别是在仓库的规模、物料的规格、包装、形状、市场销售等诸多方面存在的差异性，需要我们在实际生产过程中加强具体的实用性研究。因此本文主要考虑汽配件仓储特点，基于汽配件入库频率等因素建立仓储货位优化模型，以实现汽配件仓储货位优化，满足生产对汽配件的配送要求。

1 汽车配件仓库的货位优化问题

1.1 货位优化思路

汽车配件库的仓储管理货物品类相对较多，对于高架立体仓储区在存储策略选择方面适宜采用分类管理策略，把不同的货物进行归类处理，以方便管理(见图1)。

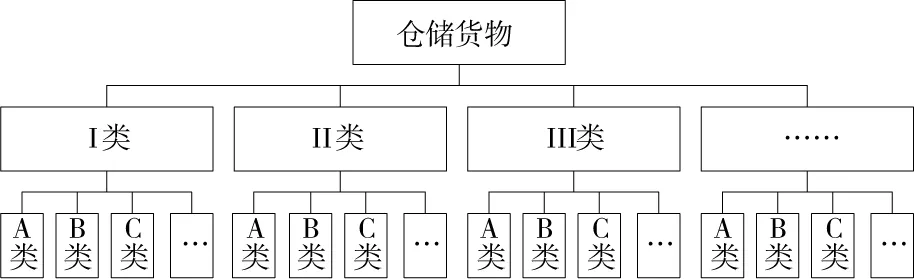
图1 货物归类示意图Fig.1 Goods classification diagram

在实际优化中本着为取而存的思想，首先将货物分为若干大类，每大类货物又包含若干小类货物，对各大类货物的平均在库量 (按每大类货物月均在库的托盘数量计算)进行统计。下面给出大类的平均在库量的统计公式，见式(1)。

(1)

式中：P为大类的货物平均在库量；p为小类货物的平均在库量。

接着在统计数据的基础上对未来一个周期的各大类货物平均在库量进行预测，根据预测结果确定该类货物需要分配的货架排数。对大类货物出入库频率(按每大类货物每月的平均出入库量计算)进行预测。

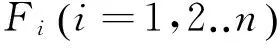
考虑到本文货位分配的依据是平均出入库频率，因此会存在某个时间段内某排货架的货物在库量超出该排货架的容量，所以分配完货架还应考虑建立适量的机动货架来存放超出部分的货物。

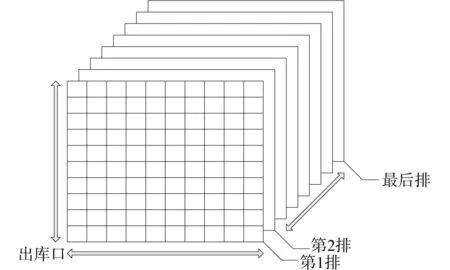
图2 立体仓货架库示意图Fig.2 Stereoscopic warehouse shelves library

最后对每排货架进行细致到货格的货位优化，每排货架的结构示意图如图3所示。

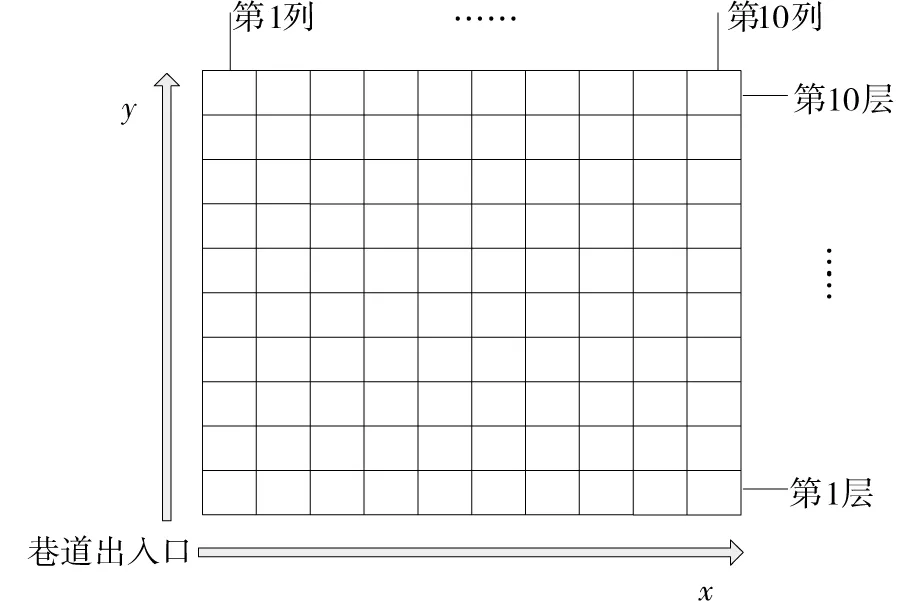
图3 货架单排结构示意图Fig.3 Shelves with single structure diagram

1.2 货位优化的流程图

为了更加清楚描述本文的优化思路，本文以流程图方式表示如图4。

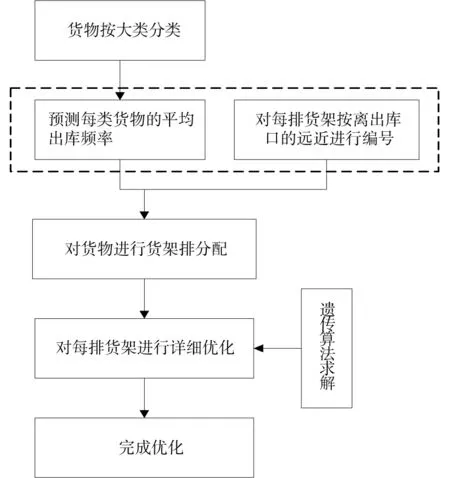
图4 货位优化思路流程图Fig.4 Flow chart of slotting optimization idea

2 汽车配件仓库货位优化模型

2.1 模型的假设

为了将研究问题简化，本文单排货架货位优化模型建立在以下假设基础上：

1)仓库每个巷道均有一台堆垛机；

2)堆垛机的行走的水平速度和垂直速度均为匀速；

3)每个货格的规格是一样的，即货格的长度和高度是固定的；

4)每一类货物的出库频率都能得到满意的预测结果。

2.2 模型中变量的定义

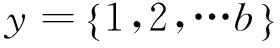
wxy为放在第x列、第y层的货物的重量；

rxy为放在第x列、第y层的货物的出库频率预测值；

txy为第x列、第y层货格的货物到达出库口所需时间；

l为货格的长度；

h为货格的高度；

Vi为堆垛机行走的平均水平速度；

Vj为堆垛机行走的平均垂直速度；

2.3 模型设计

2.3.1 目标函数一

单排货架上货物的优化最主要目的是提升订单的响应速度，这里衡量响应速度的指数当中最直接的就是时间，使出入库频繁高的货物放置在靠近巷道口处是节约出库时间的良好策略，依据上面的思想，建立第一目标函数如式(2)。

(2)

其中rxy可以由预测方法得到。

(3)

2.3.2 目标函数二

单排货架上货物的优化的同时应注意保持货架的稳定性，要遵循“上轻下重”的优化原则，该目标可以转化为所有货物的整体重心高度最低。依据以上思想，建立第二目标函数如式(4)。

(4)

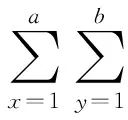
(5)

综合以上可得出单排货位优化的多目标规划的模型如下：

(6)

s.t.

1≤x≤a

1≤y≤b

x,y为整数

3 货位优化模型的算法设计

3.1 多目标优化问题描述

多目标优化(multiple objective program,简记为MOP)问题由FY Edgeworth 最先提出，V Pareto对其进行了完整的定义。在求解多目标问题时候，各个目标函数存在着相互冲突，很难求到满足所有目标函数的最优解，只在非劣解的基础上不断寻找满意解，即帕累托(Pareto)最优解。

多目标优化问题可以描述如下：

s.t.

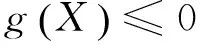
X⊂Ω

(7)

n≥2

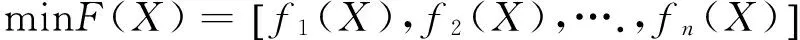
本文采用乘除法，通过目标函数的相乘使所得函数具有明确的含义，这样就把多目标函数转化成单目标函数，这个单目标函数中包含了多目标优化的意图，并利用遗传算法进行求解。

3.2 遗传算法设计

遗传算法(Genetic Algorithm,GA)最早是由Holland教授在20世纪70年代提出并发展起来的智能优化算法，具有更好的全局寻优的能力。遗传算法对种群的每个个体进行搜索，算法通过有效的设计可以跳出局部最优的“陷阱”，有利于得到全局最优解，并且全局最优的获得往往不依赖于初始解。而传统优化算法的寻优能力往往比较依赖于初始解，且不易得到全局最优。

1)目标函数的处理

本文建立的目标函数有两个，一个关注出入库的效率，另一个关注货架的稳定性。为了便于模型的求解，这里利用乘除法把两个目标转化成单个目标。则原目标函数就变成了：

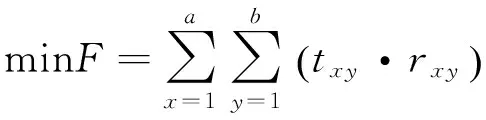
(8)

2)染色体编码

本文对单排货架上的货物采用真值编码，编码串的长度为a*b位，即编码串的长度是单排货架的层数与列数的乘积，也就是单排货架上的所有货物数。如c1c2…cn…ca*b,代表1到a*b之间所有的整数的一个排列组合，cn表示第cn个货物放在第x列第y层的货架上(其中x的取值为a整除n的商加1，y的取值为b整除n的余数)。

3)初始化种群

1到a*b之间所有的整数的一种排列组合组成了一个完整的个体的染色体，随机产生M个染色体即可组成初始种群，一般种群的规模在20～100之间。

4)确定适应度函数

适应度函数又叫评价函数，在遗传算法中适应度值高的个体遗传到下一代的概率比较大，本文的模型是求解最小值，因此需要在目标函数和适应度函数之间做出变换。由于两个目标函数的最小值均为非负，因此可以将目标函数的倒数作为适应度函数，目标函数值越大的解对应的适应度函数值就越小，这样的解被“优胜”的可能性也就会越小。

(9)

(5)选择策略

(10)

那么个体被选中次数的期望为n·p(i)。

图5 轮盘赌示意图Fig.5 Roulette schematic

6)交叉算子

在交叉运算前先将种群中的M个体以随机的方式组成[M/2]对配对，交叉操作就是在这些配对的父代中进行的。本文在交叉策略方面选取单点交叉，在个体的编码串随机设置一个点，对该点以后的部分染色体进行相互交换，对于长度为N位的编码串个体，则交叉点的位置有N-1种可能。单点交叉的示意图如图6。

图6 单点交叉示意图Fig.6 A single point of cross schematic diagram

7)变异算子

本文在编码中采用的是整数编码，为了使变异后的个体染色体仍然能表示可行解，在变异操作中选取个体染色体的指定位置上的基因进行对调(见图7)，从而既通过变异产生新个体又能保持染色体基因组的完备性。

图7 变异运算示意图
Fig.7 Mutation operation schematic diagram

8)终止条件

这里采用迭代次数达到预设的代数来判断算法是否终止。

9)算法步骤

Step1：初始化,设置控制参数和终止条件；

Step2：GenN:=0，随机产生初始种群Pop(0)；

Step3：计算初始种群个体的适应度值和目标函数值；

Step4：按照轮盘赌选择策略，从Pop(GenN)种群中选择出Pop(GenN+1)种群；

Step5：对Pop(GenN+1)种群进行交叉、变异运算，GenN:=GenN+1；

Step6：判断算法是否满足终止条件，满足则停止,不满足则转Step3，继续迭代；

Step7：输出最优解。

4 实例分析

先根据指数平滑预测方法，对仓库的货物进行预测。假定已得到库内某排货架上的16种货物(共计200托盘的量)的属性，具体如表1所示。

把以上货物按照上表中的顺序，以托盘为单位编号1～200，然后将1～200号货物随机排列作为一个初始解见下表2，表中的单元格表示该排货架某个货位对应的货物，如第二列第三层的货格对应的是第133号货物。该初始解对应的目标函数为9.216 8*108。

假设货格的长度和高度均为1米，堆垛机的垂直和水平行走速度均为1 m/s，取种群规模NIND=100，代沟GGAP=0.7，交叉概率Pc=0.7， 变异概率Pm=0.1，迭代次数为4 000代，可以得到优化后的解如表3，该优化后的解对应的目标函数值为4.684 9*108。

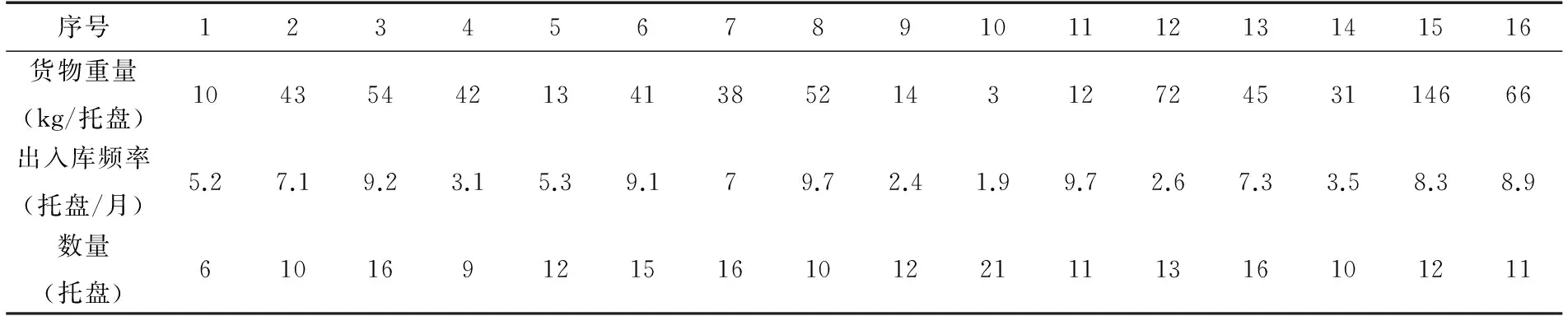
表1 某排架内货物的属性

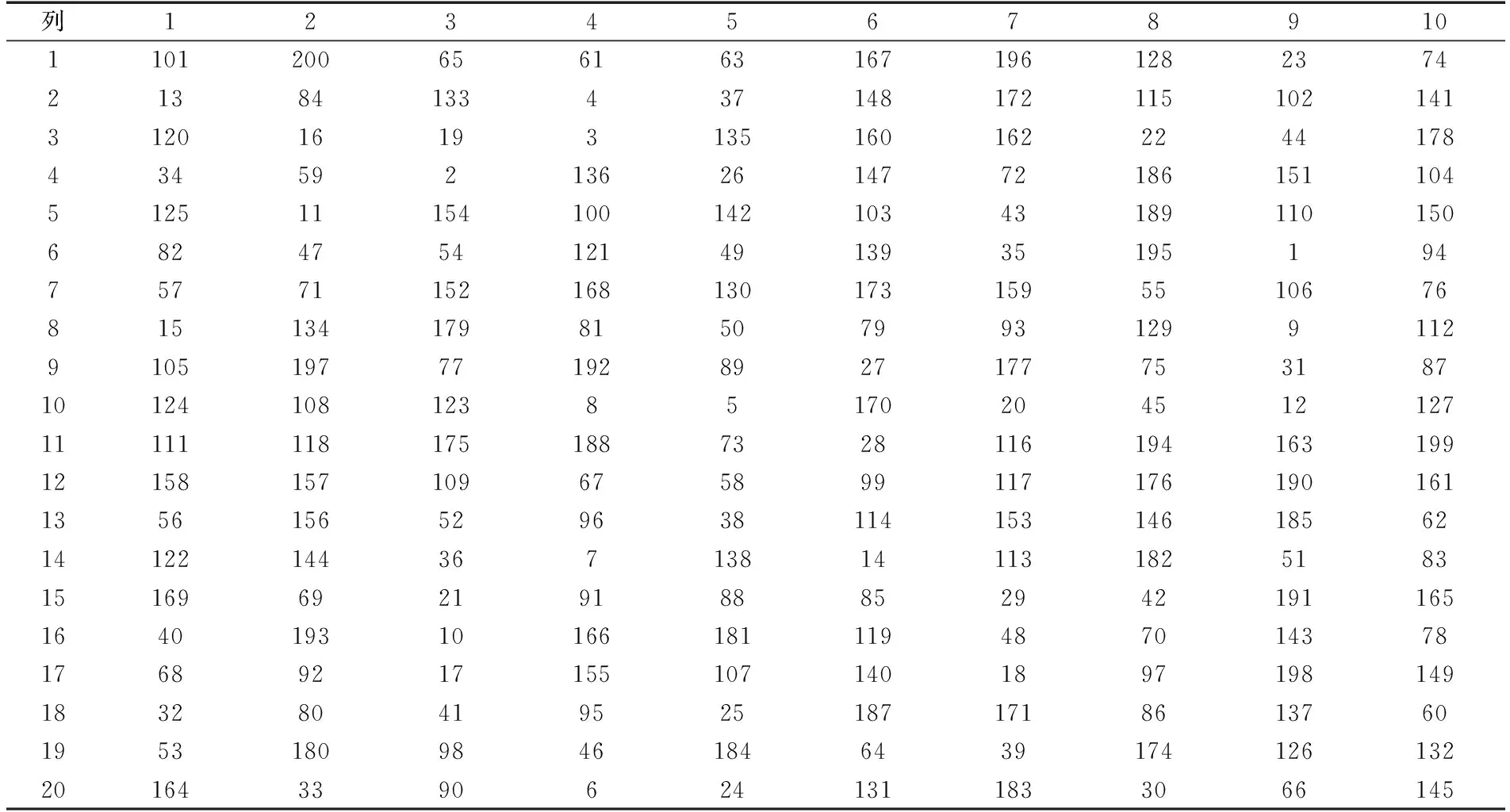
表2 货位优化前的随机初始解

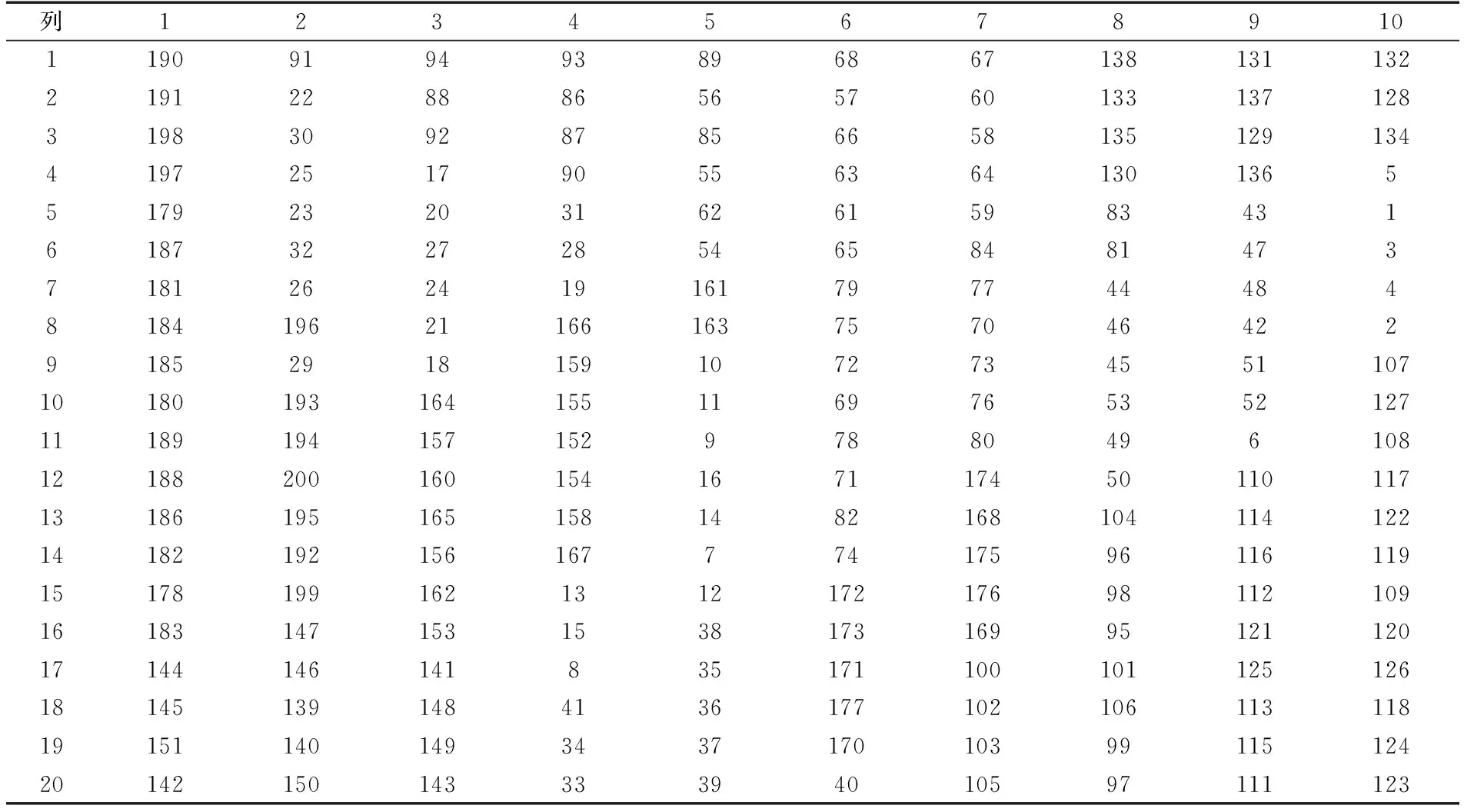
表3 货位优化后的解

由表1和表3可以看出优化后的货位较大程度上保留了货物的相关性，即属性类似的货物临近放置。

图8为算法的优化过程。

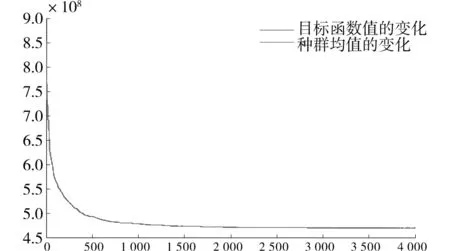
图8 算法优化的过程Fig.8 Algorithm optimization process

由图8算法的优化过程可以看出，算法在1 500代时已经较好的收敛，整个优化时间为164.25 s，优化后解的目标函数值降至原随机解的目标函数的50.83%。也就是说本文建立的货位优化模型，在保持货架的稳定性即货物的摆放遵循“上轻下重”的优化原则的同时，最大限度地把出入库频繁的货物放置在靠近巷道口处，这将极大地提升订单的响应速度。

5 结论

1)本文建立了基于出库时间和货物重心最低的货位优化的双目标优化模型，并利用乘除法将双目标函数转化为单目标函数，并设计了求解此模型的遗传算法。

2)通过遗传算法求解，优化后的目标函数值降至原随机解的目标函数值的50.83%，说明了遗传算法在解决此类问题时的有效性，为企业节约仓储成本，提高作业效率奠定了基础。

[1] Ballou R H. Enterprise logistics management:Plan,organize and control of the supply chain[M].Beijing:Mechanical Industry Press, 2006.

[2] 佘晓波. 义乌共同仓储系统设施规划与布局设计[J]. 中小企业管理与科技, 2012 (4): 275-277. SHE Xiaobo.Yiwu common storage facility planning and layout design system[J].Management&Technology,2012(4):275-277.

[3] Heskett J L. Cube-per-order index-a key to warehouse stock location[J]. Transportation and Distribution Management, 1963, 3(4): 27-31.

[4] Goetschalckx M, Ratliff H D. Shared storage policies based on the duration stay of unit loads[J]. Management Science, 1990, 36(9): 1120-1132.

[5] Graves S C, Hausman W H, Schwarz L B. Storage-retrieval interleaving in automatic warehousing systems[J]. Management Science, 1977, 23(9): 935-945.

[6] Rosenwein M B . An application of cluster analysis to the problem of locating items within a warehouse [J]. IIE Transcations,1994,26(1):101-103.

[7] Larson T N, March H, Kusiak A. A heuristic approach to warehouse layout with class based storage[J].IIE Transactions,1997，1(29):337-348.

[8] Roodbergen K J, Vis I F A. A model for warehouse layout[J]. IIE Transactions, 2006, 38(10): 799-811.

[9] Zhang G Q, Lai K K. Tabu search approaches for the multi-level warehouse layout problem with adjacency constraints[J]. Engineering Optimization, 2010, 42(8): 775-790.

[10] 罗勇，陈治亚.基于改进遗传算法的供应链金融质押物配送路劲优化[J].铁道科学与工程学报，2015，12(4)：949-955. LUO Yong,CHEN Zhiya.Distribution path optimization of pledge in supply chain finance based on improved genetic algorithm[J]. Journal of Railway Science and Engineering, 2015，12(4):949-955.

[11] 张得志，李双艳.物流节点动态布局优化模型及其求解算法研究[J].铁道科学与工程学报，2011,8(5)，96-100. ZHANG Dezhi, LI Shuangyang. Research on an optimization model for logistic nodes dynamic location and its solution algorithm[J]. Journal of Railway Science and Engineering, 2011,8(5),96-100.

[12] 谭泽波.立体仓库库位选择优化模型研究[J].中心企业科技，2007(10)：56-58. TAN Zebo.Warehouse location optimization model of choice[J].Enterprise Technology Center,2007(10):56-58.

[13] 董溪哲.仓储货位优化模型及算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2006. DONG Xizhe.Models and algorithms for warehousing slotting optimization[D]. Harbin:Harbin Institute of Technology, 2006.

[14] 王建.基于遗传算法的仓储货位优化研究[D]. 西安: 西安建筑科技大学, 2009. WANG Jian. Genetic algorithm basedwarehousing slotting optimization[D].Xi’an:Xi’an University of Architecture and Technology,2009.

[15] 吴璟,苏强.基于路径、周转率、拣货成本系数的线性规划在货位优化中的应用[J].中国高新技术企业，2011(9)：46-48. WU Hao, SU Qiang. Based on the path,turnover,cost coefficient of linear picking planning application in slotting optimization[J]. Chinese High-tech Enterprises, 2011(9):46-48.

[16] 郑凌莺.医药物流中心仓库货位优化系统的研究[D]. 上海: 上海交通大学, 2005. ZHENG Lingying.The research on medicine logistics center warehouse slotting optimization system[D].Shanghai:Shanghai Jiaotong Unicersity,2005.

[17] 马永杰，蒋兆远，杨志民,等.基于遗传算法的自动化仓库的动态货位分配[J].西南交通大学学报，2008,43(3):415-421. MA Yongjie,JIANG Zhaoyuan,YANG Zhimin, et al. Dynamic location assignment genetic algorithm-based automated warehouse[J]. Southwest Jiaotong University, 2008,43(3):415-421.

[18] 马婷.包装产品仓储货位的优化问题研究[D]. 西安: 西安理工大学, 2008. MA Ting.Research on optimization of packaging products warehousing cargo space[D]. Xi’an： Xi’an University of Technology, 2008.

The research on auto parts warehouse slottingoptimization based on genetic algorithm

HOU Zhong，ZHENG Guohua

(School of Traffic and Transportation Engineering，Central South University，Changsha 410075，China)

Warehouse Slotting optimization is an important part of warehouse managements. In this paper, the type of accessories for auto goods, warehousing large frequencies, time needs and the number of the randomness of demand characteristics, the goods allocation and optimization problems of the auto parts library package were discussed. On the basis of the library explicitly cargo accessories of Slotting Optimization, slotting optimization mathematical model was established and the multi-objectives were added into a single objective programming problem. Finally, this multi-objective programming model was converted into a single objective programming model, and a genetic algorithm to solve this model was chosen. The results show that using this optimization strategy can effectively solve the auto package goods position optimization allocation problem.

warehouse management;slotting optimization;genetic algorithm;auto parts

2016-01-21

郑国华(1963-)，男，湖南汨罗人，副教授，博士，从事物流与供应链管理、物流系统规划设计等方面研究；Email:zgh@csu.edu.cn

F252

A

1672-7029(2016)11-2305-08