阿尔·卡西《论圆周》研究

郭园园

(中国科学院自然科学史研究所,北京 100190)



阿尔·卡西《论圆周》研究

郭园园

(中国科学院自然科学史研究所,北京 100190)

基于阿拉伯文史料,对波斯数学家、天文学家阿尔·卡西《论圆周》进行研究。该研究表明卡西利用正多边形逼近圆周的方法求解圆周率。由于对圆内接正多边形的边数、边长的精确度及圆周率的精度本质关系的认识,加之精巧的开平方算法,使得卡西将圆周率推算至较高的精度。该研究对于进一步理解《论圆周》中卡西的算法思想有重要意义。

阿尔·卡西 论圆周 圆周率 迭代算法

(续注)在抄本中,当用阿语字母表示60进制数码,要在字母的上方加上横线以区别其他文字；在数表中,当数码可以明显辨别时通常不需要其上方的横线；当利用阿语字母表示含有多个数位数码时,数位与数位之间有空位,但上方的横线是连续的。另由于阿语是从右往左书写,因此相关数码的书写及运算顺序均是从右向左。

关于60进制数码的单位,当结合上下文可以明确辨别时不需要额外书写,但一般情况用阿语单词表示,如下表所示：

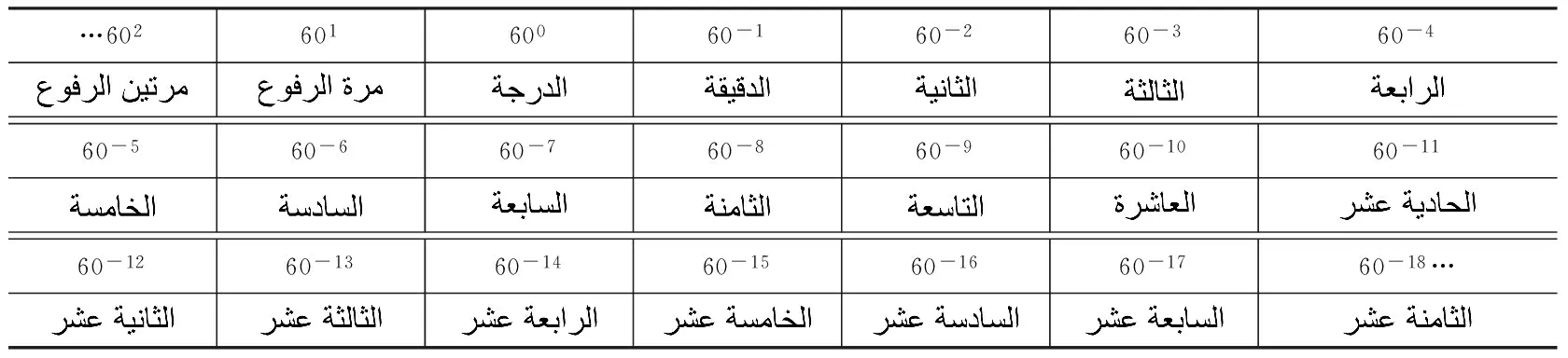
…60260160060-160-260-360-460-560-660-760-860-960-1060-1160-1260-1360-1460-1560-1660-1760-18…

据考证目前已知该书现存8份抄本[1],均为阿拉伯文书写。其中质量较高可供研究的是土耳其伊斯坦布尔抄本①Askeri Müze 756, Istanbul.和伊朗马什哈德抄本②G. al-Dīn Jamshīd M. al-Kāshī, al-Risāla al-muhītīyya. Number 162 of the mathematics collection (Number 5389 of the general collection) of Holy Shrine Library in Mashhad, Iran.。土耳其学者萨利赫·穆拉德(Salih Mourad)曾基于伊斯坦布尔抄本对该书进行过研究,后来他将研究成果告知史密斯(David Eugene Smith,1860～1944)。通过史密斯1925年的作品,西方世界第一次知晓卡西的此项工作。1949年,阿拉伯数学史家勒基(Paul L. Luckey,1884～1949)同样仅基于伊斯坦布尔抄本,首次将该书译为德语并进行了初步研究。直至其去世后的1953年,该德文译本[2]才出版,同时附有校订后的印刷体阿拉伯原文。由于伊斯坦布尔抄本第4、5两节中的29张开方算表多处数据模糊无法辨别,故在勒基提供的阿拉伯语校订部分仅包含第1、2、15、25四张算表③在参考文献[1](87～88页)中,霍根迪耶克通过对伊斯坦布尔抄本、勒基提供阿拉伯文校本和马什哈德抄本进行比对得出：伊斯坦布尔抄本含有较多错误,且在数表部分大量数据模糊无法识读,而这些问题是马什哈德抄本中没有的。勒基的校本对伊斯坦布尔抄本中的多处错误进行了修改,并且最终得到了马什哈德抄本的证实,表现了勒基优秀的阿拉伯文献研读和校订能力。。1954年罗森菲尔德(Boris A. Rosenfeld)和尤什科维奇(A. P. Youschkevitch, 1906～1993)将卡西部分著作译为俄文并出版④B. A. Rosenfeld and A. P. Youschkevitch, Al-Kāshānī, Istorico-matematiches kie Issledovaniya, Volumu VII,Moscow, 1954. 转引于参考文献[3],258页。；1956年罗森菲尔德又将其中的《论圆周》和《算术之钥》两本书重新翻译⑤Dzhemshid Giyaseddin al-Kashi, Klyuch Arifmetiki, Traktat ob Okruzhnosti[Key to Arithmetics, Treatise on the Circumference], Per. B. A. Rosenfeld, Comm. A. P. Youschkevitch, B. A. Rosenfeld. Moskva: Gosudarstvennoe Izdatelstvo Tekhniko-teoreticheskoi Literatury, 1956. 383～424. 转引于参考文献[3],258页。。[3]关于《论圆周》的翻译,罗森菲尔德仍然是基于伊斯坦布尔抄本进行的,并且附上了抄本的影印图片,其中第4节开方数表部分仅包含其中的前两张数表。

后来伊朗学者夸巴尼(A.Qurbānī)首次发现了质量更高的马什哈德抄本(图1为该抄本首页),并于1971年完成了一本关于卡西在数学和天文学领域成就的专著*A. Qurbānī, Kāshānī nāmeh[A monograph on Ghiyāth al-Dīn Jamshīd Mas’ūd al-Kāshī], Tehran University Press, Tehran, Iran, 1971. Revised edition 1989. 转引于参考文献[5],78页。。其中关于《论圆周》一书,夸巴尼基于马什哈德抄本、勒基和罗森菲尔德的研究写了一篇波斯文摘要。夸巴尼在去世前不久将马什哈德抄本的副本提供给霍根迪耶克(Jan P. Hogendijk),霍氏对此进行了较为深入的研究。在其2009年的文章[1]中,霍氏指出在《论圆周》现存抄本中,马什哈德抄本的质量最高、最接近卡西手稿,随后霍氏着重利用马什哈德抄本对勒基的阿拉伯文校本和德文翻译分别进行了部分修订并将马什哈德抄本的影印图片附于文章后。另,2004年,美国学者艾札瑞(K. Azarian)基于马什哈德抄本,将《论圆周》第1节译为英文[4]；2010年,艾札瑞基于马什哈德抄本和夸巴尼的上述著作写了一篇关于《论圆周》主要内容的摘要性文章[5]。

图1 《论圆周》马什哈德抄本首页([1], 152页)

下文中笔者主要基于勒基提供《论圆周》阿拉伯文校本、霍根迪耶克的相关校订工作和马什哈德抄本影印图片*虽然《论圆周》马什哈德抄本质量较高,但由于是阿拉伯文手写体,笔者无法识读每一处细节。故笔者首先对勒基提供的印刷体阿拉伯文校本进行全面的解读和翻译,随后参照了参考文献[1]中霍根迪耶克基于马什哈德抄本对勒基校本的40处非重要词汇的修改。,同时结合卡西另两本数学著作《论弦与正弦》和《算术之钥》中的相关内容,对以往研究比较薄弱的圆周率数值算法部分展开分析。

1 问题的源起——《论圆周》的介绍部分

在《论圆周》介绍部分中,卡西简要叙述了以往三位著名的数学家阿基米德(Archimedes,287～212 B. C.)、阿布·瓦法(Abu’l-Wafā’al-Būzjānī,940～998)和阿尔·比鲁尼(Abū Rayhān al-Bīrūnī,973～1050后)的相关工作。卡西首先指出阿基米德在其《圆的度量》(MeasurementofaCircle)一书中通过圆内接正96边形,及与其相似的圆外切多边形得出：

圆的周长小于三倍直径加上其七分之一,大于(三倍直径)加上直径的七十一分之十。二者之间的差值为四百九十七分之一,即若圆的直径为497腕尺、或497指、或497法尔萨赫,则此时圆的周长误差为1腕尺、或1指、或1法尔萨赫。([2],75页)*本段中涉及长度单位的量值及其换算关系,详见下文中关于《论圆周》第3节的论述。

接下来针对阿布·瓦法的工作,卡西指出：

阿布·瓦法将圆周分为360度,首先求出半度所对弦长,随后将其乘以720便得到圆内接多边形周长,圆外切多边形求法与之类似。若直径为120,则圆周的整数部分为376,分数部分大于59(60-1),10,59,小于59(60-1),23,54,12,二者差值为12(60-2),55,12。([2],75页)

紧接着卡西指出单位圆中0.5°弧所对弦长的准确值为31(60-1),24,56,58,36,而此处阿布·瓦法的错误取值为31(60-1),24,55,54,55,关于这点将在《论圆周》的结论部分中说明。类似地,阿尔·比鲁尼利用其得出的单位圆中2°弧所对弦长2(600),5,39,43,36,求得圆内接180边形的周长为6(600),16,59,10,48,0,同理求出相似外切180边形的周长为6(600),17,1,58,19。卡西指出2°弧所对弦长恰为正弦表中sin1°值的2倍,但比鲁尼的取值有误,准确值应为2(600),5,39,26,22。这点同样在结论部分加以说明。

尽管卡西指出了阿布·瓦法的错误,但是他并未明确该数据究竟是源于阿布·瓦法的哪本著作。据库巴尼考证*A. Qurbānī, Kāshānī nāmeh[A monograph on Ghiyīth al-Dīn Jamshīd Mas’ ūd al-Kāshī], Tehran University Press, Tehran, Iran, 1971. Revised edition 1989, 137. 转引于参考文献[5],79页。,卡西很可能参阅了纳西尔·丁·图西(Nasīr al-Dīn al-Tūsī,1201～1274)的著作Taksīral-Dā’irā,该书是阿基米德著作《圆的分割》(DivisionoftheCircle)一书的阿文译本。其中图西有这样一段论述：

……例如,假设点C为圆心,弧AB为圆周的1/720。连接弦AB,根据前面的定理和阿布·瓦法的运算,弦AB等于31(60-1),24,55,54,55。若圆直径为120,则前面的值可以被视为半度弧所对弦。接下来,如果我们将此弦视为圆内接(正)720边形的边长,则此多边形周长为376(600),59,10,59,……

此数据与卡西指出阿布·瓦法的错误数据完全相同。另通过对阿布·瓦法著作Kitābal-Kāmil*该书为托勒密《至大论》的一个简化版本。的研究,韦普克(F. Woepcke,1826～1864)*F. Woepcke, Sur une mesure de la circonférance du cercle, du aux astronomes arabes, et fondée sur un calcul d’Abol Waf, Journal Asiatique, 5m série, tome 15, 281～320. 转引于参考文献[5],79页。认为上述图西所述弦AB的量值在阿布·瓦法看来仅为一个正弦值,并非弦长。即便如此,至少也可以说明阿布·瓦法所推算弦表的数据是不准确的。另据库巴尼考证*A. Qurbānī, Kāshānī nāmeh[A monograph on Ghiyīth al-Dīn Jamshīd Mas’ ūd al-Kāshī], Tehran University Press, Tehran, Iran, 1971. Revised edition 1989, 138. 转引于参考文献[5],79页。,卡西关于比鲁尼错误数据的论述应源于比鲁尼的著作Qānoūnal-Mas’ūdī。在该书第5卷第3章中,比鲁尼指出2°弧所对弦长为2(600),5,39,43,36,这与卡西前面所指出比鲁尼的错误数据相同。该值比准确值略大,比鲁尼将其视为圆内接正180边形的边长,故据此推算出来的一系列数据均是不准确的。

在介绍部分的最后,卡西给出了他所要求圆周率的精度要求,即若存在一个直径为地球直径600 000倍的假想球体,使得通过此直径所求得的圆周长与真实值之间的误差小于一根马鬃的粗细。卡西及其同时代的伊斯兰天文学家们接受托勒密(Ptolemy,约100～约170)宇宙体系,即地球的外部有一个恒星天球。通过一系列的假设和运算托勒密得出天球半径为地球半径的20 000倍。基于更新的观测数据,中世纪伊斯兰天文学家们改变了托勒密模型中的一些距离参数,但整体上是延续了托勒密体系,并得出近似的结果。在卡西《天堂的阶梯》(Sullamal-Samā’,StairwaytoHeavens)一书中假设天球半径为地球半径的26 328倍([1],77页),另卡西在《论圆周》第10节指出有人计算出天球半径为地球半径的70 073.5倍。笔者认为卡西此处选取直径为地球直径60 000倍的假想球体,是由于该数值比以往天球稍大且便于后续运算,则计算得出的圆周率在天球内部的任意圆中计算时的误差会更小。在《论圆周》第3节的开始部分,卡西重复了这一圆周率的精度要求。卡西显然不满足于前人相关运算的精度与误差,笔者认为这是《论圆周》的直接写作目的,同时卡西对前人正弦表的纠正及其所要求圆周率误差精度的选取或与当时的天文运算有关。

2 迭代算法

卡西在《论圆周》前两节中明确了其推算圆周率的迭代算法。第1节中阐述并证明了一条几何定理(图2),这是后面一系列迭代算法的理论基础,原文如下：

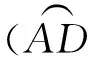
卡西对于上述定理的证明过程用现代数学符号简要表述为：

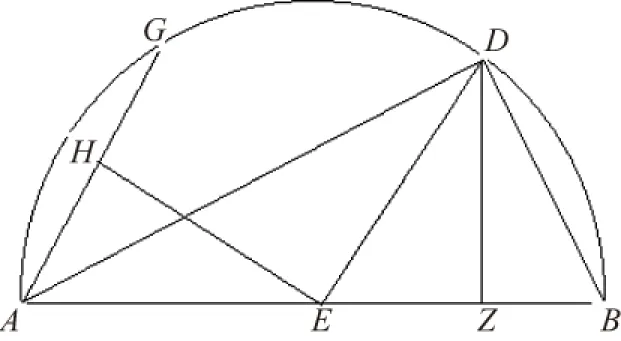
图2 《论圆周》第1节附图([2],4页)

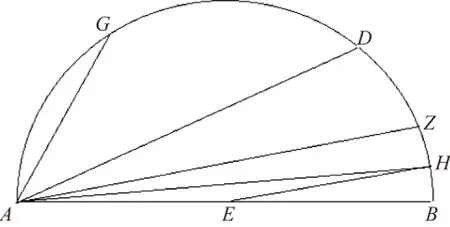
图3 《论圆周》第2节附图([2],5页)②图3与下文中的图4在原抄本中是同一幅图,图4为图3的右下部局部图,此处为了便于表述笔者将二者分开。

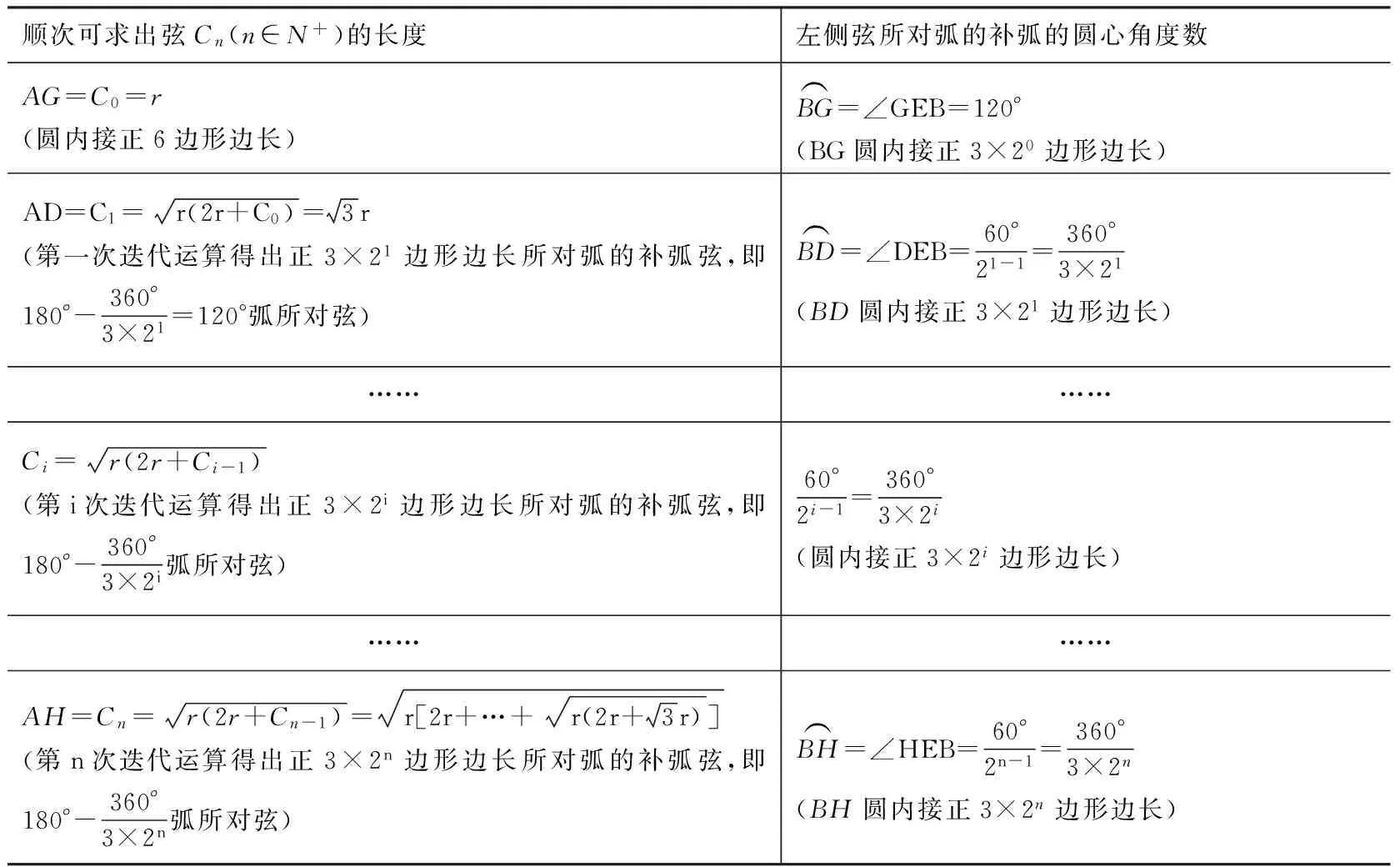
表1 《论圆周》迭代公式归纳算表

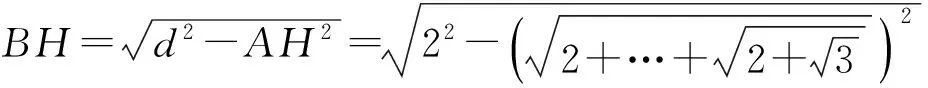
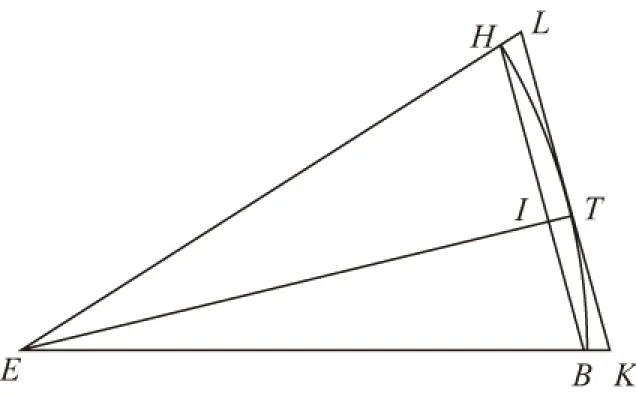
图4 《论圆周》第2节附图局部图([2],5页)

将弧BH在点T处平分,连接ET,其在点I处将弦BH平分。过点T作圆的切线TL,即过点T作ET的垂线段,在两个方向上的垂线段分别为TK、TL。连接并延长EH(与KL)交于点L; 同样连接并延长EB(与KL)交于点K。此时有KL平行于BH。其中BH为圆内接多边形边长,KL为圆外切多边形的边长,且二者*此处指两个正多边形相似。相似。([2],76页)

卡西将BH视为圆内接正3×2n边形边长,KL视为与之相似的圆外切正3×2n边形边长,随后利用相似三角形的性质求出此外切正多边形周长。卡西的推导过程利用现代数学符号简要表述为：

若AH、BH可知，则圆外切正3×2n边形周长可知。

虽然卡西在《论圆周》中对圆周率自身特点并没有相关的直接描述,但他却在其1427年成书的《算术之钥》[6]第4卷(图形的面积与体积计算)第4章(圆及其相关图形的计算)第2节(圆的面积及周长与直径之间的互化)的开始部分关于圆周率有这样一段论述：

我们知道圆的周长等于直径的三倍再加上一个直径的分数倍,此部分小于直径的七分之一,但是在计算过程中为了方便起见通常取其为七分之一。阿基米德告诉我们这个值小于七分之一,大于七十一分之十。通过运算,我们已经在《论圆周》一书中得到了一个较为精确的结果,当圆的直径为1时,圆周长为3(600),8,29,44。前面所述的值要比阿基米德给出的范围精确得多,但是这仅仅是更加接近真实值,除了万能的真主,谁也无法得到真实值…([6],147页)

这显然是卡西对于圆周率无限不循环特性的一种简单朴素的认识,接下来卡西重复了《论圆周》介绍部分所预设的圆周率精度,他叙述道：

现在有一个(假想)球,其直径为地球直径的600 000倍,则其周长同样为地球周长的600 000倍。要求其周长,为了使误差不超过一根马鬃的粗细,则需要将圆周分为多少边形？在运算过程(每次开方运算需要)精确到什么数位？([2],77页)

由上可知,《论圆周》并不是要求出圆周率尽可能精确的数值,而是要满足某种精度要求。为了解决上述第一个问题,卡西首先将该假想球体上的大圆周除以360,得出每度弧长；随后将所得除以60,得出每分度弧长,如此继续下去,连续8次除以60,最终得到1×60-8弧长小于一根马鬃的粗细,如表2所示：

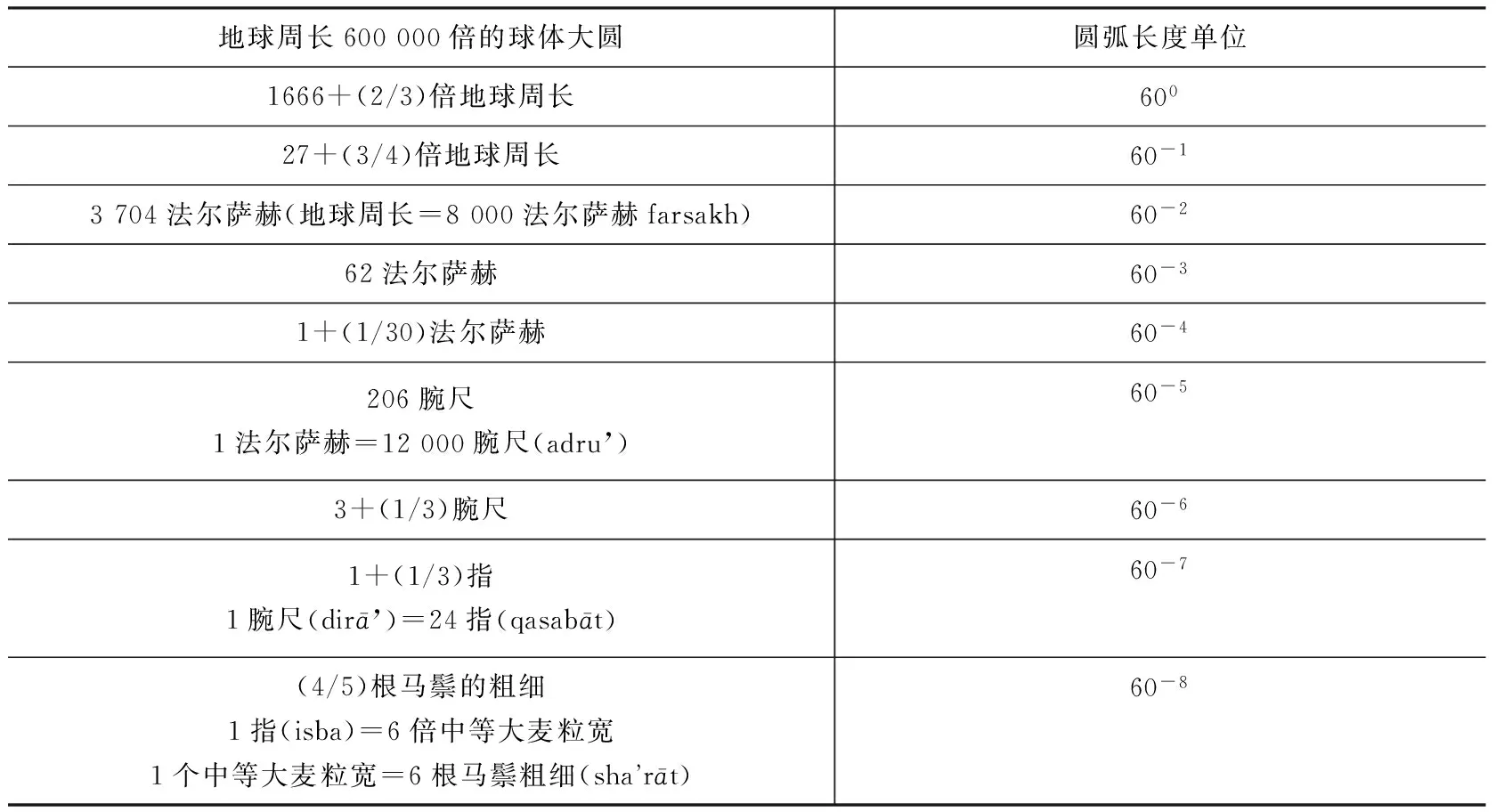
表2 求地球直径六十万倍假想球体大圆中圆心角为1×60-8所对弧长表([2],77页)

接下来当圆周为360度时,卡西引入了满足前面误差精度的一个必要条件——互为相似的圆内接、圆外切正多边形周长差等于1(60-8),则在前面假想大圆的内接与外切正多边形的差值不会超过一根马鬃的粗细,进而利用二者算数平均数表示的圆周与真实圆周长的差值会更小。卡西对选取此必要条件并没有做解释,事实上前面运算过程中涉及的4个初、终量,具备如下的比例关系：

笔者认为上式左侧相比两个量的单位是长度单位,而右侧的两个量是角度单位,它们各自的比值所表示预设的误差率是相等的。卡西此处利用角度的概念在保持预设精度要求的同时巧妙地连接了由长度单位表示的所求大圆周和下面将要涉及的单位圆周。接下来卡西在圆周为360度的圆中经过连续缩放运算,为了达到前面的预设精度,所求圆内接正多边形的边长应小于8(60-4)。笔者将卡西所给缩放运算过程列表3如下：

表3 圆周为360度的圆中满足预设精度内接正多边形边长上限估值表*此表中所有线段及圆弧的单位均为角度单位。

卡西在上述估算过程中,每一步均进行了近似取值。若按照卡西的上述思路整体对圆内接多边形边长a的极大值进行估算：

a2=d2-(2×弦心距)2=(d+弦心距)·(d-弦心距)

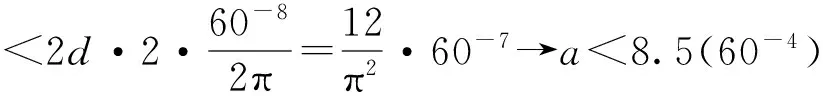
显然卡西经过连续缩放得到a<8(60-4)是合理的。为了使得圆内接正多边形边长小于8(60-4),卡西继续列表运算：从圆内接正三角形开始将其边数连续加倍,同时相应将其每边所对弧长连续减半,经过28次运算最终得到圆内接正3×228边形每边所对弧长达到要求,如表4所示：

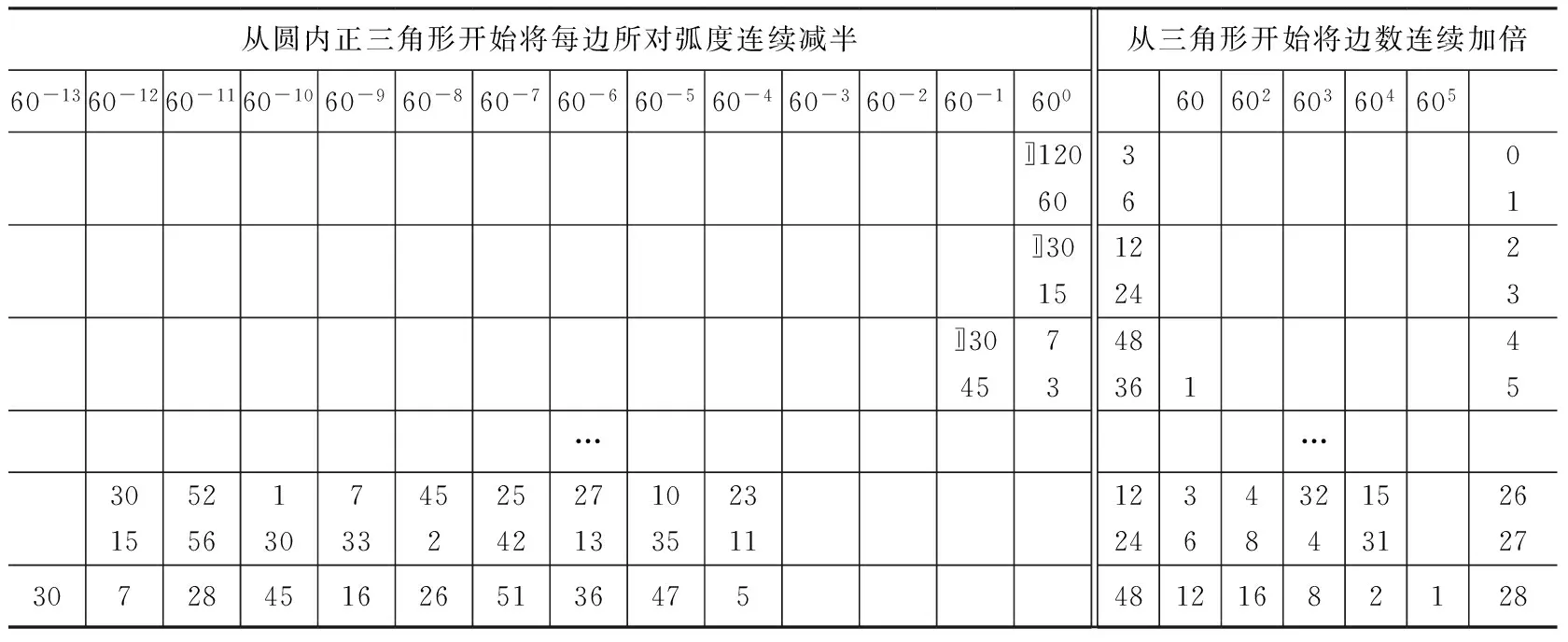
表4 圆内接正多边形边数确定表([2],79页)*原抄本及勒基提供的校本中此数表中的数据是完整且连续的,此处为了示意说明将中间部分行数据略去。

至此卡西得出当圆周为360度时,为了满足圆内接、外切正多边形的周长差小于1(60-8),圆内接、外切正3×228边形满足要求,其每边所对弧长等于5(60-4),47,36,51,26,16,45,28,7,30。另由上下文可知,若从圆内接正3×2边形入手,经过28次连续将边数加倍的迭代运算可以得出每边的长度,随后乘以边数3×228便可以得到内接多边形周长,进而求出圆周。若迭代运算次数少于28次,即多边形的边数不足3×228,则无论其边长如何精确都无法满足前面的精度要求；若迭代运算次数等于28次,则将多边形的边数精确运算到某一数位后,随后乘以边数则可求出满足预设精度的圆周率,但是即使向后继续运算并不会提高圆周率后续数位的精确度；若迭代运算次数多于28次,虽然将多边形的边数精确运算到某一数位后,将其乘以边数可求出满足预设精度的圆周率,但是会造成运算量的浪费。另外通过卡西的构造思想,笔者得出当圆周为360度时,满足互为相似的圆内接、外切正3×2n边形的周长差小于其他数量级时所对应逼近圆周的多边形边数,如表5所示：

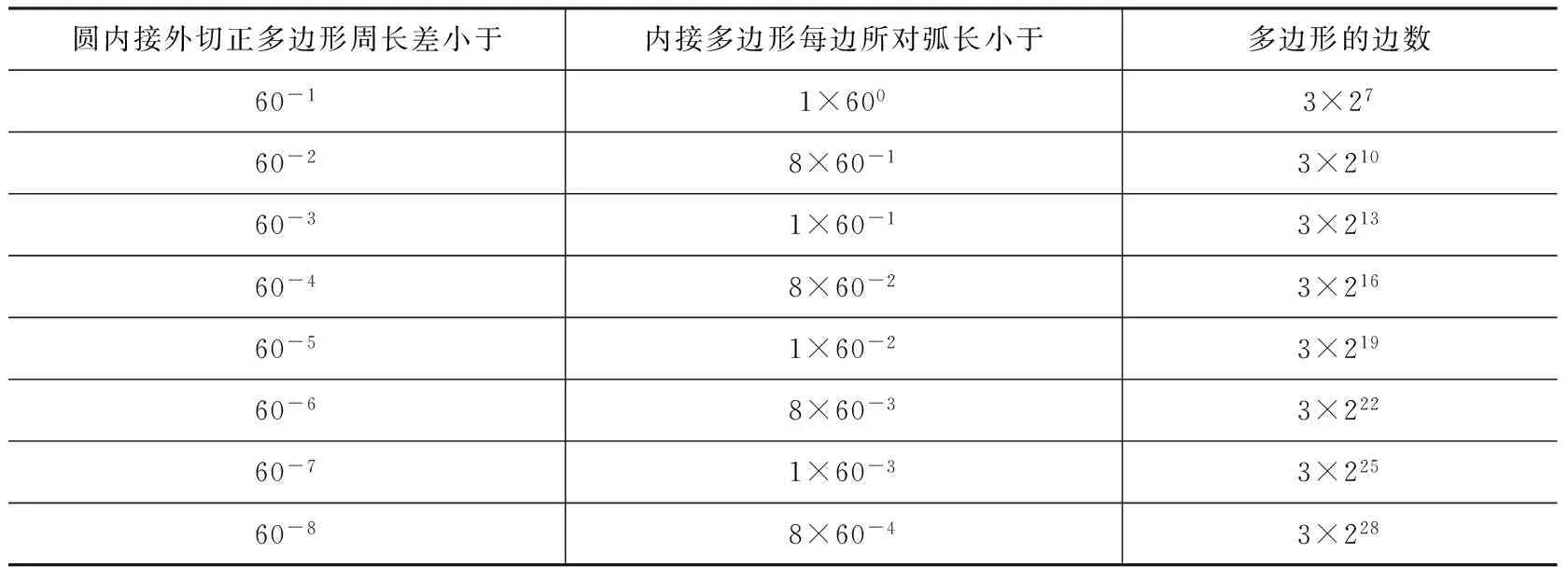
表5 圆内接、外切正多边形周长差小于其他低阶数量级时多边形边数对应表

接下来卡西叙述道：

此时每条弦均小于7(60-4),这是在圆周为360(60°)的情况下。若取直径为120,则圆周不超过其七分之一的三分之一。设存在圆内接正多边形,其边数为800 335 168,即1(605),2,8,16,12,48。([2],80页)*在伊斯坦布尔抄本和马什哈德抄本中用印度数码表示的正多边形边数均为800 335 168,但实际上3×228=805 306 368。霍根迪耶克认为这是卡西在手稿中就出现的错误,导致后来的抄本均出现错误,但由于在《论圆周》后续的运算中是利用六十进制数码(3×228=1,2,8,16,12,48)进行,故不影响最后的结果。([1],87页)

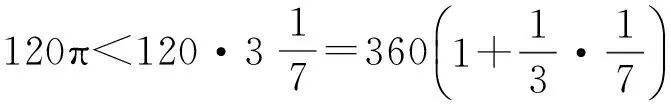
故被开方数的最后一个单位为60-13×60-4=60-17。在前面28次迭代开方运算中,由被开方数的n位有效数字开方得出其平方根的n位有效数字,故每次开方运算的精确值应达到60-17；另保留一位约算数位,故卡西得出每次开方运算的精确值应达到60-18。换言之,在利用圆内接正3×228边形逼近圆周,即进行28次迭代运算的前提下,若每次开方的精确度不足60-18,则最终通过圆内接正多边形来求解圆周所体现出的圆周率达不到前面的精度要求,但是至少可以保证已求出数位结果的准确性；若每次开方的精确度超过60-18,由于前面限定3×228边形,并不会因此而提高圆周率60-8以后数位的精度。

很明显卡西通过预设的圆周率误差精度,首先准确地确定了圆内接正多边形的边数以及每次开方的精确数位,这样既满足了精度要求同时也减省了不必要的运算。由前可知,通过圆的内接、外切正多边形周长来推算圆周率的方法早已有之,但是前人并没有明确多边形的边数、边长的精确度以及圆周率的精确度之间的关系。卡西对于三者之间本质关系的准确把握表明他在该方法的认识上已经达到了较高的理论水平。

3 精巧的开平方算法

《论圆周》第4节是其数值算法的核心,卡西首先叙述道：

将2(601)加到正六边形边长,即1(601)上,得到3(601)；再将其进一位得到3(602)；取其平方根再加上2(601)。将所得之和再次进一位,并取其平方根,重复28次相同的运算。([2],80页)

随后卡西指出在开平方运算中要利用“准数法”(mījān)和将所得平方根平方来检验运算的准确性。除此之外没有过多的论述,之后便是28张连续的迭代开平方算表。由于这些算表算法、结构相同,故此处仅以第一张算表——求解3(602)平方根为例进行说明。如上文所述原始算表中的数码单位是利用阿拉伯语表述,其数码是利用阿语字母表述,故运算书写顺序整体上是从右至左、从上至下进行(图5)。

图5 《论圆周》第4节第一张开方算表马什哈德抄本影印图片([1],142页)

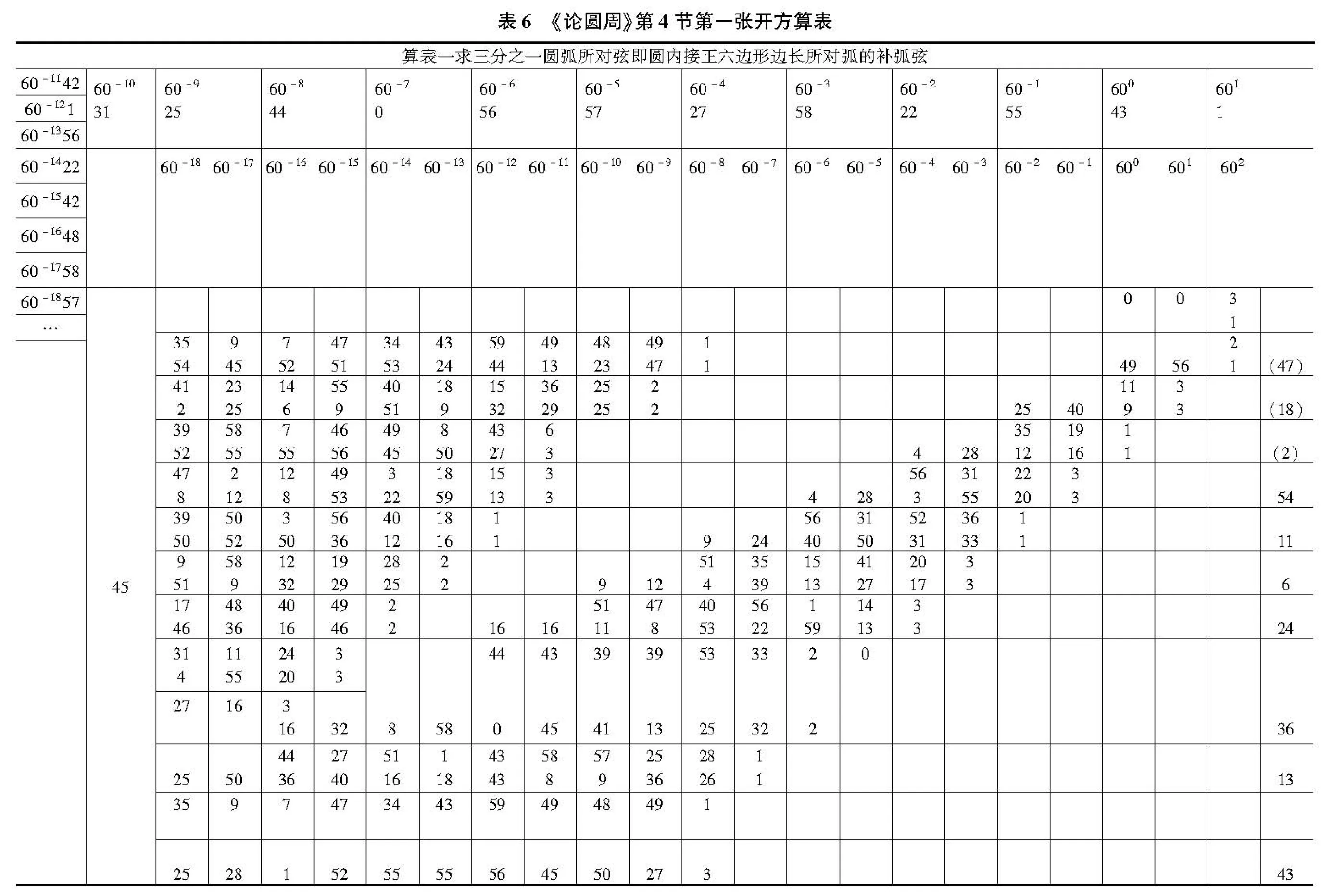
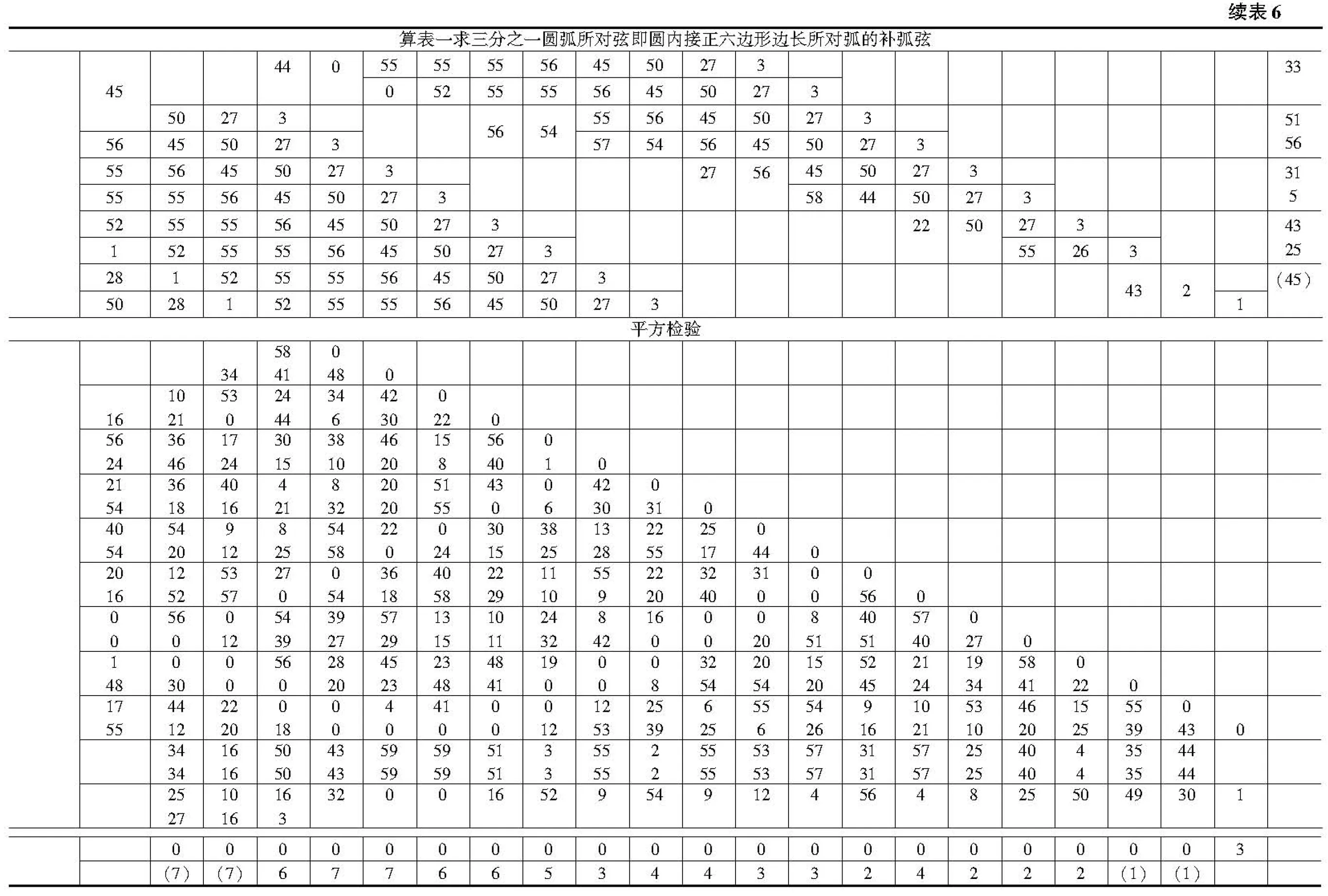
接下来基于图5和勒基提供阿拉伯文校本中的相同算表*勒基提供阿拉伯文校本中的此算表见文献[2],81页；另在勒基的德文译本中将此算表([2],12页)左右颠倒重新编写,笔者在表6中保持了原阿拉伯文抄本中从右到左的书写和运算顺序。,笔者将此算表中的数码全部转写为今天的印度阿拉伯数码,如表6所示。

下面笔者对该算表中涉及的相关算法展开分析。

3.1 精巧的开平方算法

表6整体上分为上下两部分,上部为开平方算表,下部将所得平方根自乘来复原被开方数进行检验。在上部的开方算表中,卡西采用了一种与传统中算“增乘”开方算法类似的算法。在阿拉伯数学史上,早期阿拉伯数学家萨马瓦尔(Al-Samaw’al,约1130～约1180)[7]、

萨拉夫·丁·图西(Sharaf al-Dīn al-Tūsī,1135～1213)[8]都使用过该算法,此外卡西在《算术之钥》第1卷第5章(整数的开方)、第2卷第10章(分数的开方)和第3卷第5章(六十进制数码开方)中,对利用上述算表开方有详细的论述*关于卡西此种形式开方算法过程、算法原理及其历史演变可以参考笔者的另外两篇文章：《〈算术之钥〉与中算若干问题的比较研究》(《自然科学史研究》,2013年第1期,107～128页)、《〈算术之钥〉之代数学研究》(上海交通大学博士学位论文, 2013年)。。尽管卡西不是此算法的原创者,但是从现有史料来看,阿拉伯早期数学家们均是给出与中算相似的分散的算表,卡西却将所有分散的算表整合在一起,他自己的解释是便于运算和检验。笔者按照《算术之钥》中相关算法将上述开方算表中前面几步机械算法复原,如表7所示：

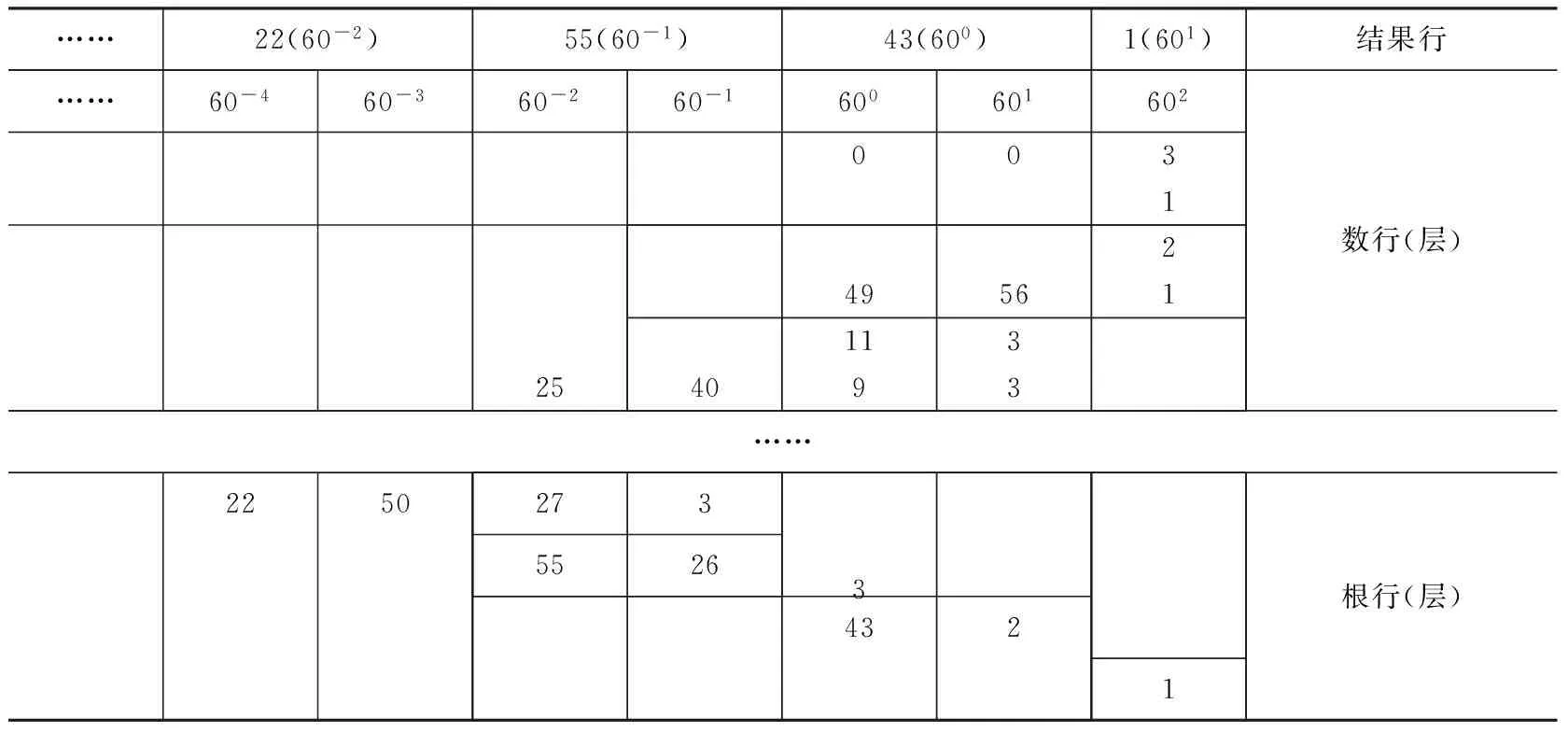
表7 《论圆周》第4节第一张开方算表局部*表7为表6的右上部局部表。

(1)首先写出被开方数3(602)并作表格。从600开始将被开方数分节,其中每节中所含数位的个数等于所要求开方次数,故3(602)被分为两节,首节为数字3(602),次节为0(601),0(600)。其中每一节的第一个数位为被开方数的有理数位,本题中600、602为有理数位,剩余数位称为无理数位。随后在竖直方向上分层,层数等于开方次数,每两层间作水平分割线,每一层的宽度由实际运算需要决定。本题应分为两层,上半部为“数行”,下半部为“根行”,“数行”之上也就是表格的最上方称为“结果行”。

(2)从第一节3(602)开始,试求出0～59中最大的整数,可以从3中减去此数的平方,得到1。将其写在结果行中本节的有理数位上,同时写在根行中与其对应的列。用上面的数字1乘以根行中的数字1,把乘积写在数行被开方数对应位置的下方,即该节有理数位所在列。随后将二者相减,在下方写出二者之差2,在此之前要在二者之间作一条水平分割线用以表示此线上部的数字将被擦去。随后将结果行的数字再次加到根行的数字上,所得和写在原有数字的上方并后(左)退一位,即位于601所在列,在此之前要在二者之间作一条水平分割线用以表示线下方的部分将被擦去。故数行中的运算方向是由上至下,而根行中的运算方向是由下至上。

(3)接下来再次寻找0～59之间的最大整数,即次商x,使得[2(601),x]与x(600)的乘积能够从前面被开方数的剩余部分2(602)中减去,得到43(600),将其写在结果行第二节的有理数位上,同时写在根行中分割线上方对应位置上。用它乘以根行中的数字,将结果写在被开方数剩余部分的下方并从中减去,如果没有得到这样的数字,则在结果行中前面所述的次商位置上写零,同时将根行中的数字继续后退一位,如前继续运算。本例中根行数字为[2(601),43]乘以43(600)得到1(602),56,49写在数行中被开方数剩余部分2(602)的下方并从其中减去,剩余3(601),11。接下来将上方的数字43(600)再次加到根行对应数字上,得到3(600),26,退位如前。

(4)对本题而言,3(602)开平方至单位600时无法开尽,卡西称之为“无理根”。如若得到其精确的方根,需要在其左侧,即低阶数位上补充数字零。例如开平方需要在接下来的两个连续数位上补充数字零；如果是开立方,则连续三个数位上添加数字零,以此类推。如果需要更为精确的方根,可以继续添加数字零,其中开方的次数应为被开方数低阶数位所添加数字零个数的约数,且添加的零个数越多,结果越精确。本题中在60-1及60-2两个数位上添加零作为下一数节,其中60-2为本节有理数位,后面的运算同前。

3.2 开方法中的估商方法

显然按照上面的开平方算法,每进行一次估商运算,整个算表在竖直方向上需增加三行数据、在水平方向上需向左增加两列数据,直至运算至60-18。但是由于题目数据的特殊性,随着被开方数剩余部分以及根行中数字数位的逐渐增加,通过上面算表及《论圆周》下文第7节可知卡西从第4次估商开始,仅需利用被开方数中剩余部分的前三位数码除以根行中的前三位数码便可以准确地求出新的估商。笔者据此将随后每次估商过程复原,如表8所示：

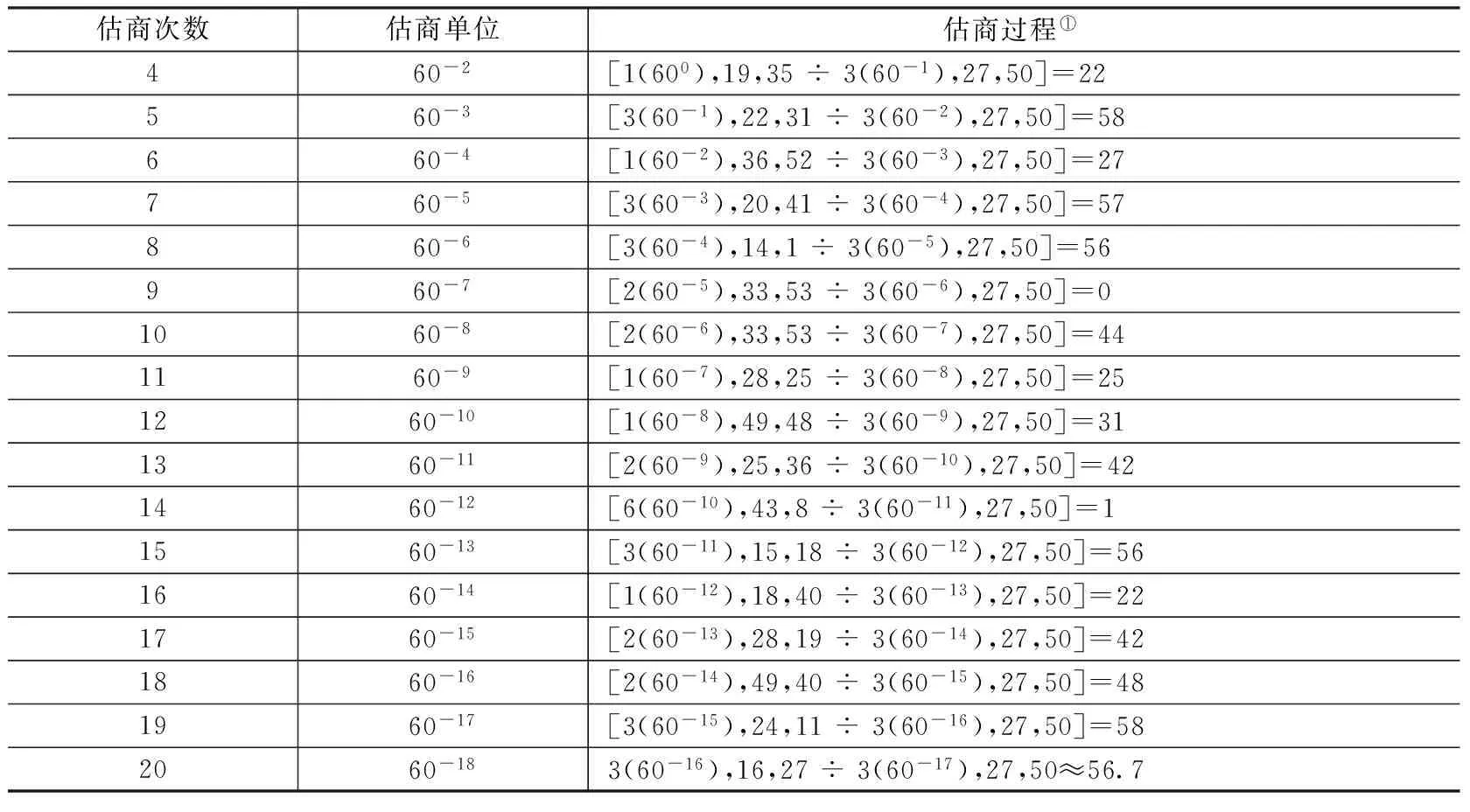
表8 《论圆周》第4节第1张开方算表结果行中60-2～60-13除法估商表

①该表格第三列中的“[]”为取整符号。

3.3 算表结构的调整

若按照传统开平方算法,如图6所示,笔者将原算表数据分为1、2、3、4共计4部分,形成两个同底的三角形结构。其中1、3为数行层,2、4为根行层。

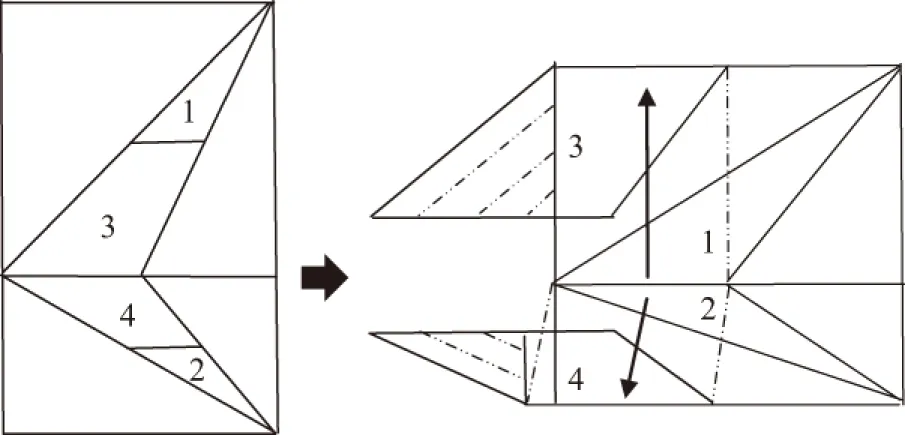
图6 《论圆周》迭代开方算表上部结构图

卡西利用上述估商的特殊性,首先将两个同底的三角形数据结构在竖直方向上进行调整：从第12次估商开始,将被开方数的剩余部分35(60-18),9,7,47,34,43,59,49,48,49,1(60-8)按照图6中右侧上部箭头方向移至数行顶部；同时将根行数字50(60-19),28,1,52,55,55,56,45,50,27,3(60-9)按照图6中右侧下部箭头方向移至根行底部且向左后退一位。在图6中可见卡西保持原有1、2两部分不变并将二者底边靠拢,将3、4两部分移至原有数表中的空白部分。随后在水平方向上,由于在60-10至60-18共计9次估商过程采用的是将被开方数剩余部分的前三位除以根行数字的前三位,故将不需要的图中阴影部分数据略去。通过这样数据结构的转变,在保证结果准确性的同时减省了运算空间与运算量。

3.4 检验算法之一：“准数法”(mījān)

要保证第4节28张开方算表中每一个数据的准确性并非易事,为此卡西进行了两类保证其准确性的运算——准数法和平方检验法。对于前者,在《论圆周》中卡西仅提及了其名称,但是在《算术之钥》第1卷有关十进制整数算术的第9章中对此有详细的论述：

检验计算的正确性可以利用准数法,如果运算准确则准数法一定正确,而没有必要将原来的问题重新计算。该方法是将某个数字的每一位上的数字相加,从结果中逐个减去数字9,直至剩余的差为9或者小于9,此即为原数的准数。例如要求数字64578的准数,将数字8、7、5、4、6相加后逐个减去数字9,剩余3,此即为原数的准数。对于两数乘积的准数等于乘数的准数乘以被乘数的准数,然后将所得乘积逐个减去数字9,剩余的差应等于原乘积的准数,这种方法可以用来检验乘法运算的正确性。([6],76 ～77页)

此方法不仅适用于十进制整数运算,在《论圆周》中同样可用于检验六十进制数码运算的准确性，此时需要将每个数位上数字相加并逐一减去59。我们截取前面开方算表6开始部分的部分数据来说明,如表9所示。

卡西第二次估商得到43(600),将其同时写在结果行及根行中；随后将其乘以根行的数字,把乘积写在被开方数下方并从其中减去。在此过程中需要检验乘法运算：[2(601),43]×43(600)=1(602),56,49的正确性。被乘数[2(601),43]的准数为45,将其写在表格同行的右侧,乘数43(600)的准数为43,二者相乘有：45×43=1 935=59×32+47；另原乘积1(602),56,49的准数同样为(49+56+1=106=59+)47,此时两个准数相等,故原乘法运算正确,剩余同理。随着迭代算法的进行,开方结果逐渐逼近2(601),算表中乘法运算数据逐渐“简单化”,从第20张算表开始卡西便不再需要该算法进行检验。

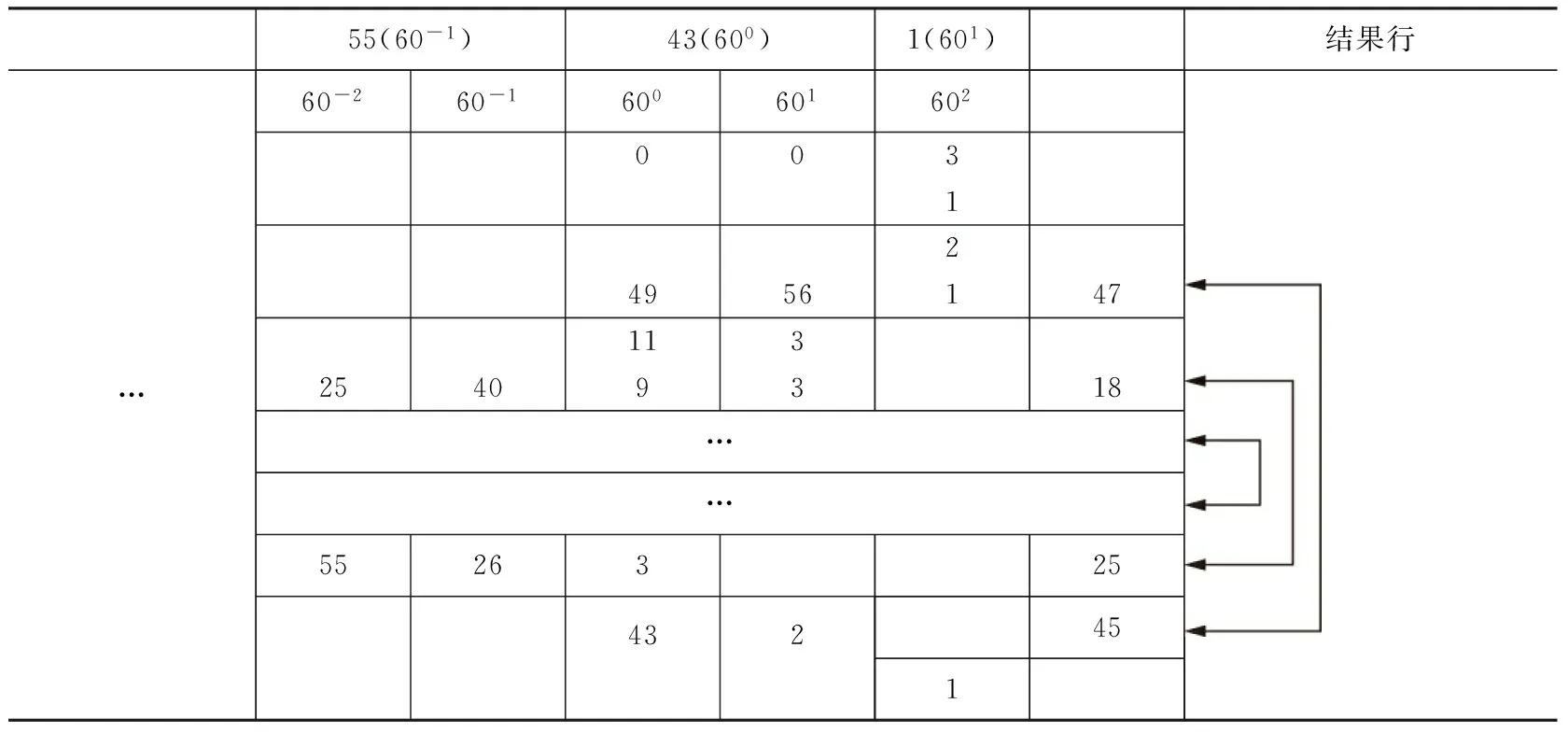
表9 《论圆周》第4节第1张开方算表中“准数法”示意算表*表9为表6的右上部局部表。

3.5 检验算法之二：平方复原法

如果说准数法是用来保证容易发生错误的每一步乘法运算的准确性,那么“平方检验法”便是用来保证28张算表中每一张算表运算的准确性。该算法体现在每张算表的下部,上下两张算表在相同列中数据的单位相同,这样便于运算和检验。所谓的“平方检验法”并非“严格”将所求得的平方根进行平方,随后观察所得结果是否为原被开方数。由于在开方过程中算表结构进行了调整,同时略去了部分数据,故该检验法进行了适应性的调整,以第1张算表为例,整体的原则是将从被开方数3(602)中减去的数相加,最后加上被开方数中的剩余部分3(60-16),16,27,所得和应还为原被开方数3(602)。笔者将平方检验数表按照其运算顺序抽象为图7所示。

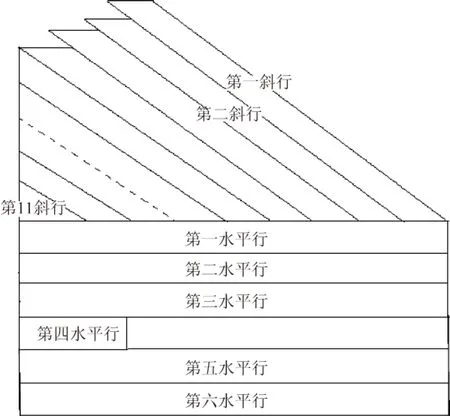
图7 《论圆周》第4节迭代开方算表下部结构图

卡西首先从上部斜行开始运算,第一斜行由下至上分别为平方根的首位数字1(601)顺次乘以平方根中剩余每一位上的数值,直至58(60-17)；第二斜行由下至上分别为平方根的第二位数字43(600)顺次乘以平方根中剩余每一位上的数值,直至58(60-17) ……第四斜行由下至上分别为平方根的第四位数字22(60-2)顺次乘以平方根中剩余每一位上的数值,直至58(60-17)；从第五斜行开始,继续上面的运算规律,但是由于卡西在开平方过程中略去了部分数据,故每一斜行的数据依次减少一个,即第五斜行最后的乘积终止于58(60-3)×48(60-16)；第六斜行终止于27(60-4)×42(60-15)……最后第11斜行仅为25(60-9)×31(60-10)。另由于在开平方过程中部分数据进行了舍入运算,故在平方检验算表的最左侧部分数据进行了适应性的调整。

此时将11个斜行数据在竖直方向上相加,把所得结果写在第一水平行中；由于在每次估商运算后,一次项系数要加倍后退位,故应从被开方数中减去上面所得和的二倍,故此时在第二水平行中将上一行中的数据重新书写；在第三水平行中还应加上从被开方数中减去的部分估商的平方,从右至左分别为1(601)的平方、43(600)的平方……直至25(60-9)的平方；在第四水平行中加上被开方数中剩余部分3(60-16),16,27。最后将4个水平行中的数据相加得到原被开方数3(602),并写在第五水平行,说明原开方运算正确。原抄本在第六水平行中为印度数码书写,每个数字表示上方斜行部分在竖直方向相加时需要进位的数值。*例如在上方斜行部分左侧第四列将要进行加法运算的数值为：58,41,24,44,30,15,4,21,8,25,27,0,54,39,56,0,0,18,6(其中最后的数字6为第六水平行左侧第四列位置的数字)相加得到470=7,50。其中非进位数字50写在第一、二水平行左侧第四列的位置；进位数字7写在第六水平行左侧第五列的位置,随后与上方斜行部分第五列中的数字相加。《论圆周》第4节28张迭代开方算表所得结果统计如表10所示：

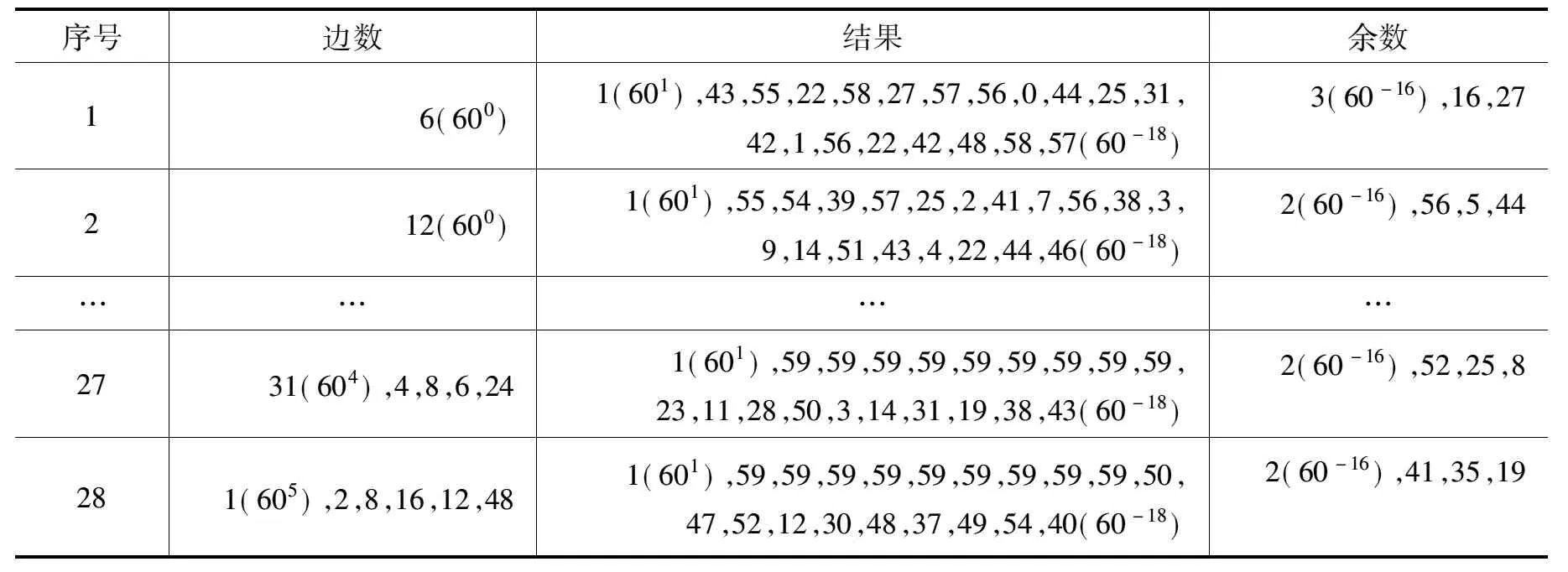
表10 《论圆周》第4节28张迭代开方算表结果统计表([2],9～10页)*勒基在其德文翻译部分所给此数表中的数据是完整且连续的,此处为了示意说明将中间部分行数据略去。

另在此算表的第5、6、7、8行均出现了两行数据,现以第5行中部分数据为例来说明其排列规律：

……59×8=52,71×8=8,06×8=48,0 …………14×8=52,14×8=32,0……

4 《论圆周》的剩余部分

在《论圆周》第5节中仅包含求解圆内接正3×228边形边长的开平方算表①在勒基提供的阿拉伯文校本中并没有包含第5节的算表。,即利用勾股定理,从直径的平方中减去第4节中第28张算表所得平方根的平方②用直径的平方4减去第28张算表所得平方根的平方,等价于用2减去第27张算表所得平方根,随后求所得差的平方根。此处看似不需要第28张算表,但是第4节仍然计算第28张算表的原因是为了第6节中求解圆外切正3×228边形边长所需。,随后将所得进行开平方运算：

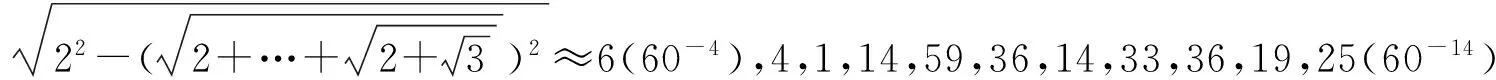
《论圆周》第6节首先讲述的是求解半径为60个单位长度的单位圆中互为相似的圆内接、外切正3×228边形周长。在求内接多边形周长时,卡西将第5节中的开平方结果乘以其边数3×228=1(605),2,8,16,12,48,运算过程如算表11所示：

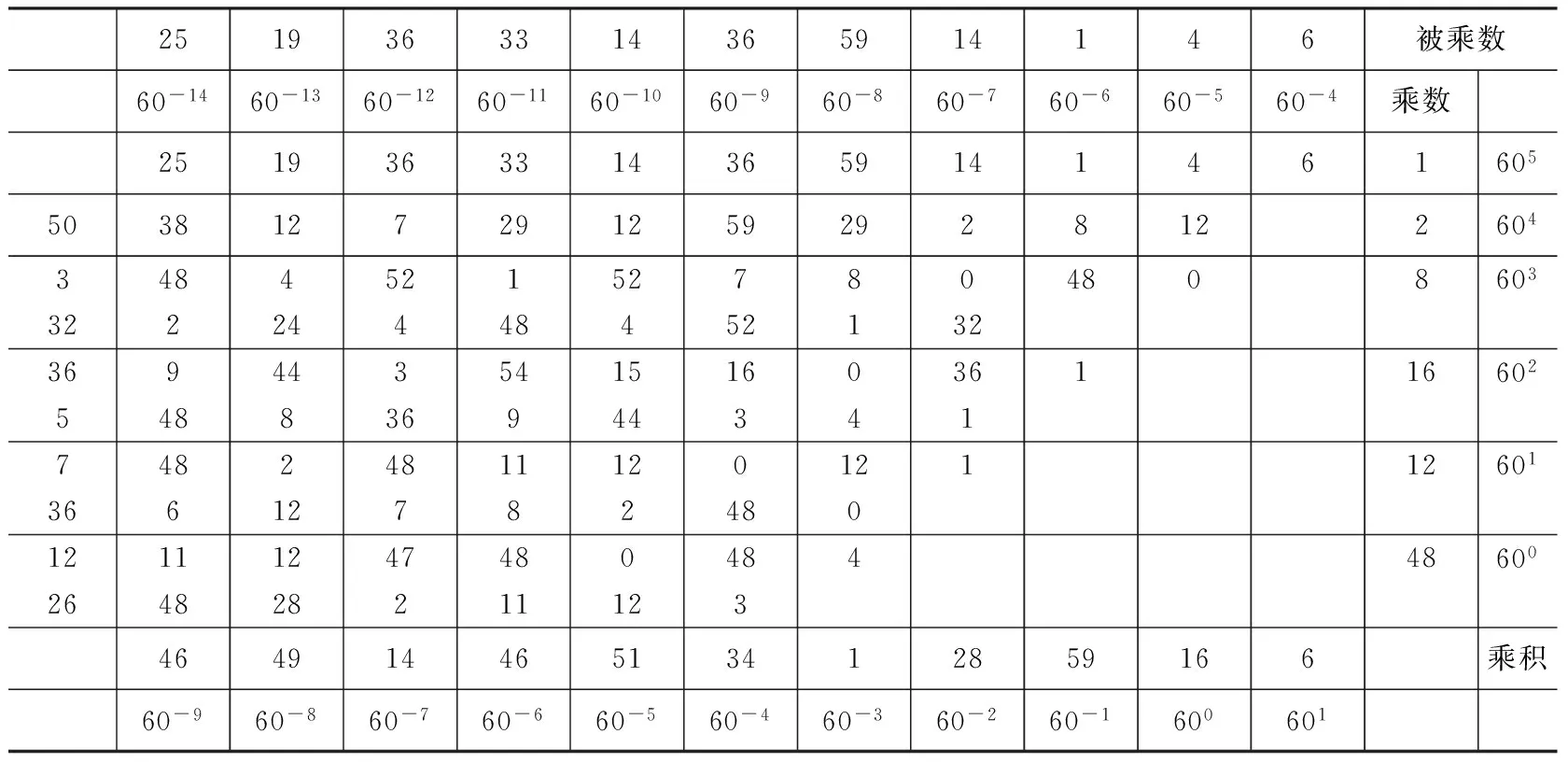
表11 《论圆周》第6节求2π乘法表([2],83页)③此处利用表格进行乘法运算的基本步骤是将乘数与被乘数所有数位上的数字按照顺序写在矩形表格相邻两边；随后将乘数每一数位上的数字乘以被乘数每一数位上的数字,把乘积写在相应交叉位置的格中；最后在竖直方向上将所有乘积相加并写在表格下方,此即为最后乘积。这种利用表格进行乘法运算及相应的除法运算在《论圆周》第9节以及《算术之钥》中多次出现。

随后卡西利用第2节中内外多边形周长的比例关系来求圆外切多边形周长：

其中第一项首位单位为601,第四项首位单位为60-9,二者乘积为60-8；将其除以第三项首位单位600,得到第二项首位单位为60-8。此处由于低阶单位的数字对于运算结果的首位精度没有影响,故将低阶单位数字略去,则上述运算简化为：

将圆内接、外切正3×228边形周长差29(60-9)加到内接多边形周长6(601),16,59,28,1,34,51,46,14,49,46(60-9)之上,得到圆外切多边形的周长为6(601),16,59,28,1,34,51,46,14,50,15(60-9)。由上文可知当圆周为360度时,圆内接、外切多边形的周长差小于1(60-8)度时,满足通过地球直径600 000倍的长度为直径所求圆周的误差小于4/5根马鬃的粗细；在上述单位圆中,圆周约为376.8,内接、外切正多边形周长差小于29(60-9),相对于所求大圆而言,此时内接、外切多边形周长差小于2/5根马鬃的粗细；若利用二者算术平均数来表示圆周,则圆周的真实值与所求值之间的误差小于1/5根马鬃的粗细,满足前面的精度要求。第6节最后卡西指出当单位圆半径为60时,此时圆周为：6(601),16;59,28,1,34,51,46,14,50。若半径为1,则圆周数值不变,但单位要后退一位,即相当于卡西所给2π的取值为：6(600),16,59,28,1,34,51,46,14,50。将此数分别乘以1至60之间的每个数字并列表*在勒基提供的阿拉伯文校本中并未包含此算表,马什哈德抄本中包含此算表([1],110页)。,这样便于通过半径求圆周或是通过圆周求半径等的相关运算。另在《算术之钥》第4卷第4章第2节(圆的面积、周长与直径间的互化)中附有一张类似数表([6],149页),其中π的取值仅为3(600),8,29,44。

卡西在第7节中主要说明第4节中的28张算表精确到60-18已经能够满足预设精度要求,即使再往后精确计算一位,对预设的误差精度不会产生影响。卡西首先指出：

第一张算表的最后一位是正57(60-18),但真实的结果是最后一位为负20(60-19)。 这是由于最后一次运算时将剩余的3(60-16),16,27除以两个平方差中的前几位,即3(60-17),27,50,得到的商为56(60-18),40,但是前面取值仅为57(60-18)。([2],85页)

为了使第2张算表的结果继续向后精确一位,则需要在最后一步除法运算估商之前将被除数减去前面的误差。在迭代公式中每次开方运算之前,前面一次的结果乘以半径60后,所有的单位需要进一位,由于第1张算表略去的误差为-20(60-19),故在第2张算表的被开方数中要减去20(60-18)。第2张算表在最后一次除法运算之前被开方数的剩余部分为2(60-16),56,5,从其中减去20(60-18),剩余2(60-16),55,45。将其除以两个平方之差,即下方根行中的一次项系数3(60-17),51,49,得到的商为45(60-18),28。原来第2张算表的结果末位为46(60-18),故第2张算表的误差为-32(60-19)。按照此规律,卡西将上文中所有按照顺序得到的平方根及内接正多边形边长、周长都继续向后推算一位,如表12所示：

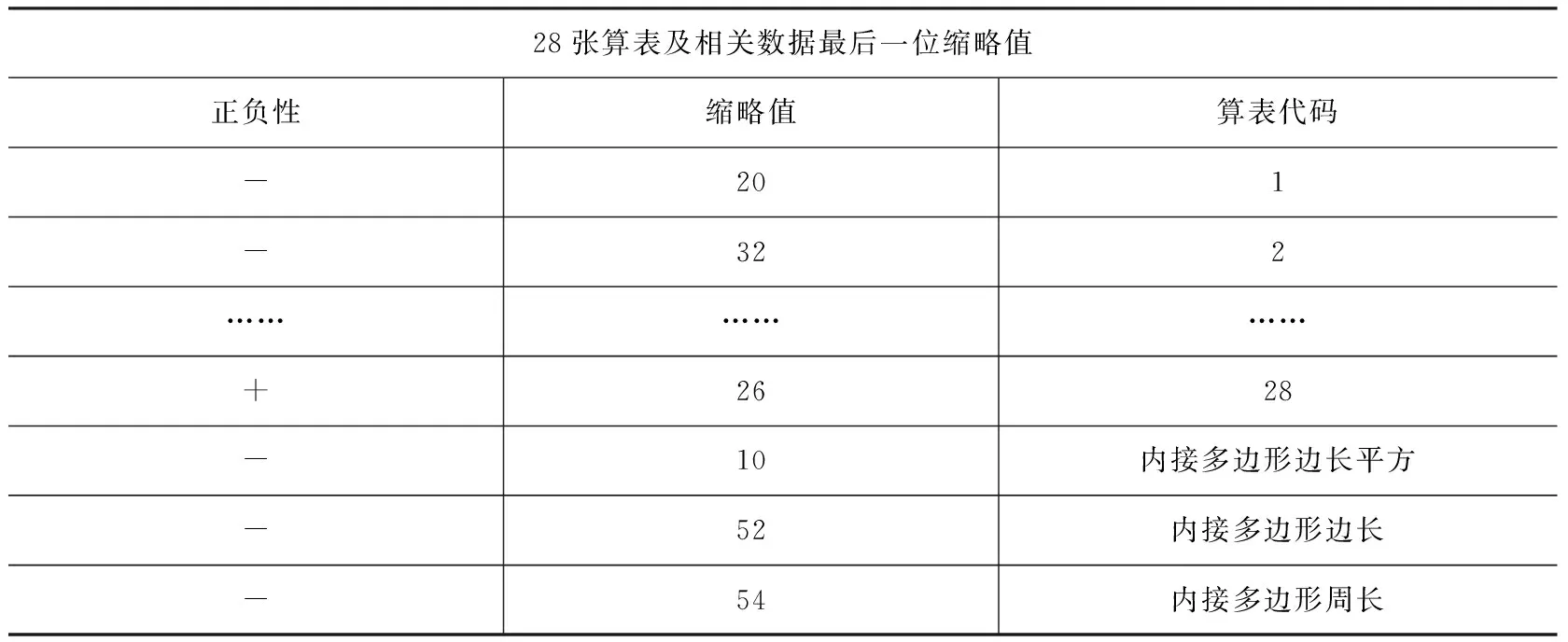
表12 《论圆周》第7节2π误差检验表([2],86页)*原抄本及勒基提供的校本中此数表是横向排列,且数据是完整连续的,此处为了示意说明将中间部分行数据略去。

由此可知,如果将圆内接正3×228边形边长继续向后推算一位,则需要在原有最后一位25(60-14)基础上减去52(60-15)；进而所得多边形周长需要在原有最后一位46(60-9)基础上减去54(60-10)。我们可以取内接多边形边长最后一位为24(60-14),周长为45(60-9),即便如此周长的误差也小于1(60-9),仍满足前面的误差精度。

在第8节中,卡西将前面求出半径为1的单位圆周长——相当于2π,直接转化为印度数码。《论圆周》并未给出具体的六十进制分数到十进制小数的转化方法,但卡西在《算术之钥》第3卷第6章中对于60进制数码与印度数码的互化有详尽的阐述,且他指出《论圆周》第8节的转化运算就是利用此法。《算术之钥》原文如下：

将六十进制数码表示的分数转化为用印度数码表示,即十进制小数。首先将六十进制数码表示的分数乘以10,此时结果中的首位数字,即“度”位上的数字为(转化后十进制小数的)十分位数字；如果此位没有数字,则在十分位补上数字0；随后将刚才结果取出整数部分(即十分位数字)后的剩余部分继续乘以数字10,如果结果中的首位数字同上满足要求,则取其作为百分位数字；如若不然,则在百分位补上数字0；随后将剩余的分数继续乘以数字10,将得到结果中(处于度单位上)的数字写在千分位上,如此继续下去。([6],123～124页)

例题：现在要将8(60-1), 29, 44转化为十进制小数,解题过程如表13所示：

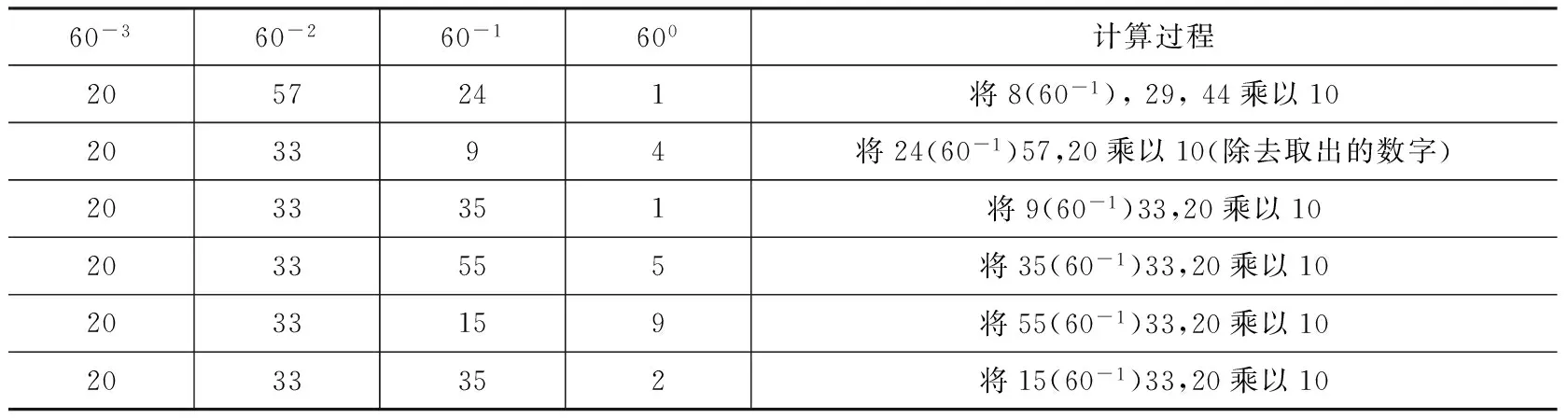
表13 《算术之钥》第三卷第6章六十进制分数转化十进制小数例题算表

由于(最后一行)乘法结果中“分”单位上的数字大于一半*此处指表13中第7行第3列数字35,其大于60的一半,即大于30,目的是四舍五入。,则将百万分位上所取的数字加1,得到3。随后将结果按照印度数码的书写方式记为：1 4 1 5 9 3,此即为所求,其中最右侧一位数字的单位为百万分位。([6],123～124页)

卡西利用上述方法得到二倍圆周率等于6.2831853071795865,随后将其分别乘以1至10之间的每一个整数,这样便于通过印度数码表示的半径求圆周,或是通过印度数码表示的圆周来求半径,如表14所示：

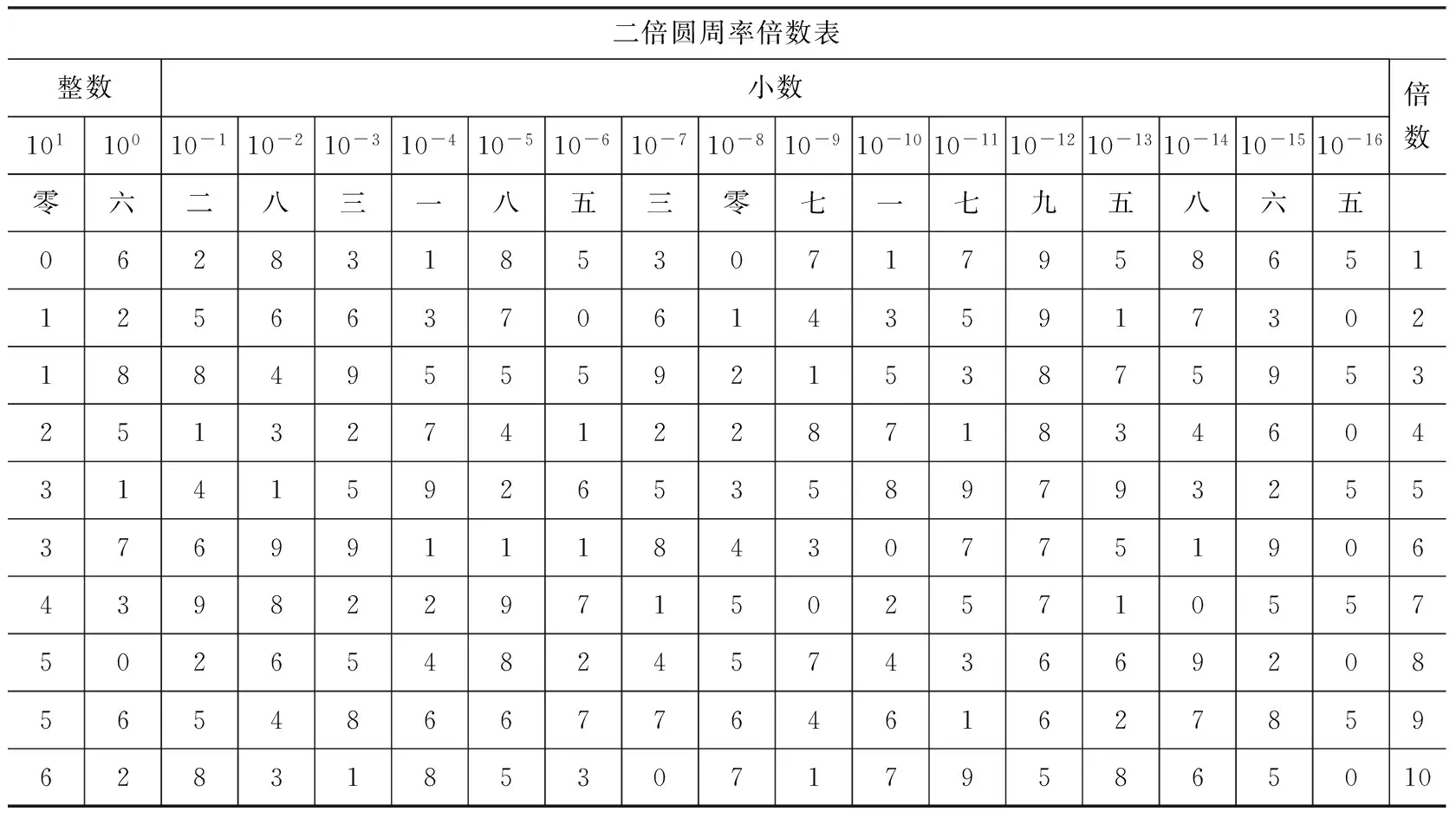
表14 《论圆周》第8节用印度数码表示2π倍数表([2],86页)

在《论圆周》第9节中卡西利用第6节和第8节中2π的两张倍数表,分别举例如何利用类似于第6节中的表格算法通过半径来求圆周,以及通过圆周来求半径。此外在《算术之钥》第5卷第4章第2节有关圆面积的计算内容中,还包含了半径与面积之间类似的表格算法。

表15 《论圆周》第10节两个2π近似值差值表([2],91页)

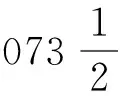
在《论圆周》结语部分,卡西主要解决了《论圆周》开始部分中所提及的阿布·瓦法与阿尔·比鲁尼在弦表中部分数据运算错误的问题,此处不再展开论述。

5 结 语

在众多古代文明中都可以找到有关圆周率推算的数学内容。卡西在《论圆周》一书中得到拥有16位准确数字的用十进制小数表示的圆周率,若仅从推算精度看,直至1596年荷兰数学家鲁道夫·范·科伊伦(Ludolph Van Ceulen,1539～1610)才将用十进制小数表示的圆周率推算至20位准确数字。圆周率的推算是一项复杂的工作,若要客观准确地评价卡西在《论圆周》一书中取得的数学成就,不能仅凭圆周率的推算精度。

由上文可知,卡西已经认识到了圆周率无限不循环的特点,在天文学及高精度运算中对圆周率的精度提出了较高要求,因此在《论圆周》开始部分就确定了圆周率的精度要求,这也是该书的写作目的。在算法思想上,卡西采用了阿基米德的方法,即从互为相似的圆内接、外切正六边形入手,将多边形边数连续加倍,相应地二者的周长逐渐逼近圆周,随后在单位圆中利用推算出的内接、外切多边形周长的算术平均数表示圆周,即二倍圆周率。在《论圆周》正文部分,卡西首先利用几何模型构造了迭代算法；随后通过对圆周率精度、迭代运算次数和迭代运算中的开方精度之间本质关系的认识,进而确定了运算量,使得在满足预设精度的同时避免了运算量的浪费。有了理论上的保证,进而卡西在《论圆周》第4节,利用28张迭代开方算表进行推算。在具体的操作过程中,卡西将已有的开方算表算法进行了适应性的改造,使得在保证运算结果准确的同时减省了运算量,体现了他高超的构造运算能力。

1 Hogendijk J P. Al-Kāshī’s determination of π to 16 decimals in an old manuscript [J].ZeitschriftfürGeschichtederArabisch-IslamischenWissenschaften, 2009, 19: 73～154．

2 Luckey P L. Der Lehrbrief über den Kreisumfang [J].AbhandlungenderDeutschenAkademiederWissenschaftenzuBerlin, 1953, 6．

3 Youschkevitch A, Rosenfeld B. Ghiyath al-din Jamshid Mas’ud al-Kashi (or al-Kashani) [C] //DictionaryofScientificBiography.Volume 11. New York: Charles Scribner’s Sons, 1981. 255～262．

4 Azarian M K. Al-Kāshī’s fundamental theorem [J].InternationalJournalofPureandAppliedMathematics, 2004, 14(4), 499～509．

5 Azarian M K. Al-Risāla al-muhītīyya: A Summary [J].MissouriJournalofMathematicalScience, 2010, 22(2), 64～85．

6 Jamshīd al-Kāshī. al-Demerdash A S, al-Cheikh M H (eds.).Miftahal-Hisab(KeytoArithmetic) [M]. Cairo: Dār al-Kātib al-‘Arabī, 1967．

7 Rashed R.TheDevelopmentofArabicMathematics:BetweenArithmeticandAlgebra[M]. Translated by Armstrong A F. Kluwer Academic Publishers, 1994．

8 Sharaf al-Dīn al-Tūsī. Rashed R. (ed. & trans.).Oeuvresmathématiques:AlgèbreetgéométrieauXIIesiècle[M]. 2 Vols. Paris: Les Belles Lettres, 1986．

A Study of al-Kāshī’sTreatiseontheCircumference

GUO Yuanyuan

(InstitutefortheHistoryofNaturalSciences,CAS,Beijing100190,China)

This article analyzesTreatiseontheCircumference(1424) by al-Kāshī (circa 1380～1429) based on related Arabic historical materials. Al-Kāshī adopted regular polygons to approximate circle circumference in the calculation of Pi. The results show that an insight into the relationship among the side number of the regular polygons, plus the side length accuracy and the precision of Pi, were crucial in al-Kāshī’s high accuracy of Pi. The results also demonstrate that the sophisticated algorithm of extracting square root contributed to his calculation. The present study is of significance in understanding the algorithm used inTreatiseontheCircumference．

al-Kāshī,TreatiseontheCircumference,Pi,iterative algorithm

2015- 01- 13；

2015- 11- 30

郭园园,1981年出生,天津人,助理研究员,主要研究方向为数学史。

中国科学院科学技术史青年人才研教特别支持项目：阿尔·卡西代数学研究(编号：Y522021009)

N091∶O11

A

1000- 0224(2016)01- 0095- 25