位似图形研究与实践

江苏省扬州市江都区吴桥中学(225232)

马 萍●



位似图形研究与实践

江苏省扬州市江都区吴桥中学(225232)

马 萍●

一、位似图形的概念

如图1所示，每幅图的两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的两个图形叫做位似图形，这点叫做位似中心，这时我们说这两个图形关于这点位似.

在图1中，△ABC与△A′B′C是以O为位似中心的位似图形，四边形ABCD与四边形A′B′C′D′是以O为位似中心的位似图形，五边形ABCDE与五边形A′B′C′D′E′是以O为位似中心的位似图形.

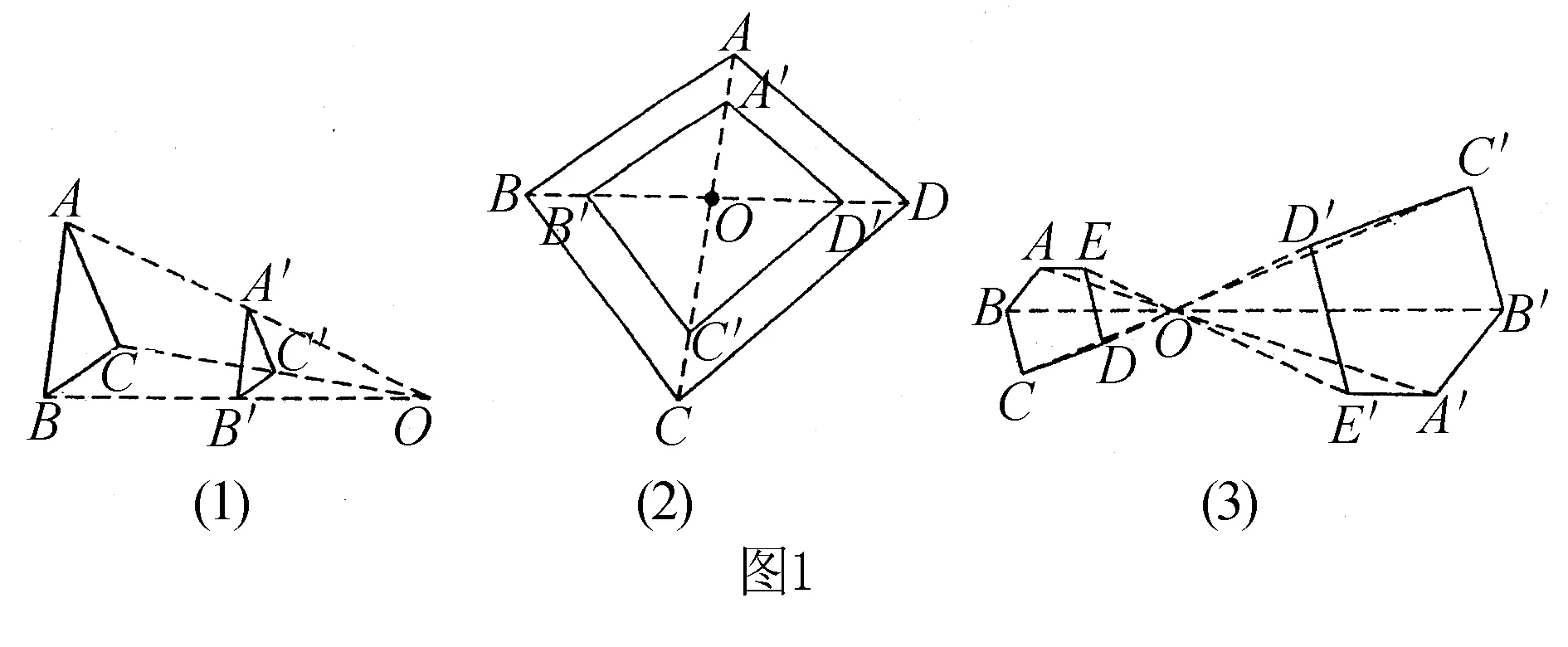
(1)位似图形一定是相似图形，而相似图形不一定是位似图形.位似图形具有两个特点：一是对应点的连线交于一点；二是对应边互相平行或在同一条直线上.

(2)两个位似图形的位似中心只有一个.

二、位似图形的性质

根据位似图形的概念，可得到位似图形的四个基本性质：(1)位似图形的对应角相等，对应边成比例；(2)位似图形的对应点的连线所在的直线相交于一点，即经过位似中心.(3)位似图形的对应边互相平行或在同一条直线上；(4)位似图形上任意一对对应点，到位似中心的距离之比等于相似比.

例1 一般的室外放映的电影胶片上每一个图片的规格是3.5cm×3.5cm，放映的屏幕的规格是2m×2m，若放映机的光源距胶片20cm，问：屏幕拉在距离光源多远的地方时，放映的图像刚好布满整个屏幕？

分析 四边形ABCD(胶片)与四边形A′B′C′D′(屏幕)是位似图形，根据对应线段的比相等，列出比例式即可求解.

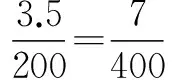
三、位似图形的判定

判断两个图形是不是位似图形，先看它们是否相似，若相似，再看两个图形对应点的连线是否经过同一点，若经过同一点，则是位似图形，否则不是位似图形.

例2 如图3所示，矩形ABCD的对角线AC与BD相交于点O，E，F，G，H分别是OA，OB，OC，OD的中点那么矩形ABCD与四边形EFGH是不是位似图形？如果是，指出位似中心，并求出相似比；如果不是，请说明理由.

解 ∵E,F,G,H分别是OA，OB，OC，OD的中点，∴EFD.

∴EF∥GH,EF=GH,∠FEH=90°.

四、位似图形实践中易误点

误点1 弄不清位似与相似的关系而出错

位似图形是特殊的相似科形，而相似图形则不一定是位似图形，只有当相似图形的对应点的连线所成的直线交于一点(位似中心)时，相似图形才是位似图形，判断两个图形是不是位似图形，应严格按位似图形的概念去判断.

例3 如图4所示，∠ADE=∠ACB,试判断△ADE与△ACB两图形是否为位似图形？

解 不是位似图形.因为∠ADE=∠ACB,且∠A=∠A,所以△AED∽△ABC.但对应点D，C的连线与E，B的连线不交于点A，对应边DE与CB也不平行，故△ADE与△ACB两个图形不是位似图形.两个图形是不是位似图形，关键是根据位似图形的定义去判断，首先两个图形是相似图形；其次是对应点的连线交于一点；然后对应边相互地或在同一条直线上.本题中图形满足第一个条件，但不满足后两个条件，易出现判断错误.

易误点2 求关于某点位似的图形时容易漏解导致错误.

在平面直角坐标系中，以原点为位似中心将一个图形按照一定的相似比k放大或缩小，有两种情况：一种是两个图形在原点的同侧，这时对应点的坐标比为k；另一种是两个图形在原点的异侧，这时对应点的坐标比为-k，求对应点的坐标时要把已知点的坐标分别乘k和-k得出两种情况下对应点的坐标，有时由于考虑不全面，容易造成漏解的错误.

例2 已知E(-4，2)，F(-1，-1)，以原点O为位似中心，按相似比1∶2，把△EFO缩小，则点E的对应点E′的坐标为( ).

A.(2,-1)或(-2,1)B.(8,-4)或(-8,-4)

C.(-2,1)D.(-8,4)

一般地，在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).

G632

B

1008-0333(2016)29-0003-01