基于模型估计的LiFePO4电池EKF滤波算法SOC估计研究

邓宫泰，马　磊，贾俊波，韩　明

(1.西南交通大学电气工程学院系统科学与技术研究所，四川成都610031；2.淡马锡理工学院清洁能源研究中心，新加坡529757)

基于模型估计的LiFePO4电池EKF滤波算法SOC估计研究

邓宫泰1，马磊1，贾俊波2，韩明2

(1.西南交通大学电气工程学院系统科学与技术研究所，四川成都610031；2.淡马锡理工学院清洁能源研究中心，新加坡529757)

常规LiFePO4动力电池组SOC(state of charge)估计方法难以同时满足复杂工况下SOC预测的可靠性与初值不敏感性,为解决该问题，提出一种针对电池组工况特性下的扩展卡尔曼滤波算法。该算法基于电池组工况放电特性，提取其特征参数并进行模式分类，根据在电池充放电时不同参数与区间，对卡尔曼滤波模型进行动态参数补偿，加快SOC向真值的收敛速度,并减少SOC估计误差,实现算法对SOC估计初值的不敏感性。最后使用美国机车工况测试UDDS标准模型，对实际采集的电池模型进行仿真实验，其结果验证了所提出的算法可行性和有效性。

LiFePO4动力电池组；SOC；能量管理；扩展卡尔曼滤波；自适应卡尔曼滤波

随着能源危机的加剧及环境的恶化，电动汽车已成为全球交通能源转型的发展方向。但动力电池组已成为阻碍纯电动汽车发展的瓶颈，其安全性和续航能力是目前面临的核心问题。在电池组管理方面，对SOC(电池荷电状态)的精确估计是保障电池组安全性能和续航能力的基础。

目前研究者已经提出一些解决SOC问题的方法和理论，如库仑计量法[1-2]，神经网络算法[3],卡尔曼滤波算法[4]等。库仑计量法容易受到系统初值误差和电流传感器的漂移以及积分时间误差等的影响，导致算法不收敛。虽然研究者提出了多种智能修正方法[1-2]，但估计精度难以进一步提升。神经网络方法[3]与模糊逻辑控制算法[4]由于需要大量的训练过程，在工程实验上仍然具有一定难度[5]。同时锂电池在放电平坦期(SOC为20%～85%)的SOC与OCV(开路电压)变化率极小，且电池模型不确定性因素大，非线性强，易受到不确定因素的干扰，而锂电池SOC初值的准确性还未能解决，单一的电池模型与算法很难表现出实际的电池工作状态，需要根据数据采集信息实时调整模型策略与算法。

一些学者在使用卡尔曼滤波量测SOC方面做了深入探讨，但其模型负载仅为恒流负载，或则没有考虑电池SOC初值误差因素，在SOC初值不准确时，卡尔曼滤波收敛过慢，无法满足系统实时性要求。

本文为解决电池组工作在复杂工况下的实际需求，在以上研究基础上，建立起硬件实验平台，测试电池在不同SOC下的模型参数，实时跟踪并更新模型参数，解决了模型参数时变的问题，提高了电池模型的准确性。同时，在扩展卡尔曼滤波算法基础上，根据电池实际运行的不一致性、采集系统噪声模型不确定性等特征，提出了Rk补偿扩展卡尔曼滤波算法，从理论上分析其可行性，并使用实验采集数据验证了该算法的有效性。

1　磷酸铁锂电池等效电路模型的建立

1.1实验平台搭建

相比于其他电池模型，等效电路模型能更直观地表现输入电流与输出电压之间的关系[6]，本文通过对电池在设定工作条件下充放电实验，建立电池的等效电路模型。实验对象为天津力神公司LR1865EC-1.35 Ah/3.6 V磷酸铁锂离子动力电池。实验平台工作电源由台湾Chroma 6Z60-60型电源提供。采用日本菊水公司PLZ1004 W可编程电子负载模拟。数据采集模块使用美国NI公司的USB-6343数据采集板。图1为实验系统结构图。

图1　实验系统结构图

1.2Thevenin等效电路模型参数辨识

Salameh等人[7]最先提出了Thevenin模型，图2为Thevenin模型等效模型。

图2　Thevenin等效电池模型

图2中，理想电压源E为电池的开路电压 (open circuit voltage,OCV)，与电池当前的SOC相关；电阻R为电池欧姆内阻；电容C与电阻Rc为电池的极化环节，其中Rp为电池极化内阻，C为电池极化电容；U0为系统输出电压。

本文使用复合脉冲功率特性实验(HPPC Test)，结合激励响应分析和最小二乘拟合法对电池不同状态下的参数进行辨识。图3为HPPC TEST实验过程中电池电流和电压曲线。此时电池SOC为80%，脉冲冲击电流设定为2倍额定电流。

0 s到10 s之间，电池电流为3 A，此时电池电压会快速下降。在10 s负载变为0 A，电压会有一段突变(ΔU),其可视作卸载电流在欧姆内阻上引起的变化(R=ΔU/I)。在10 s到40 s之间，电池电压缓慢上升，可认为是由于储存在RC支路中的电能被施放所致。通过该曲线可以计算出RC支路中极化电阻Rc，极化电容C和电池响应时间τ等参数。图4为电池在不同SOC特征值下的模型参数。

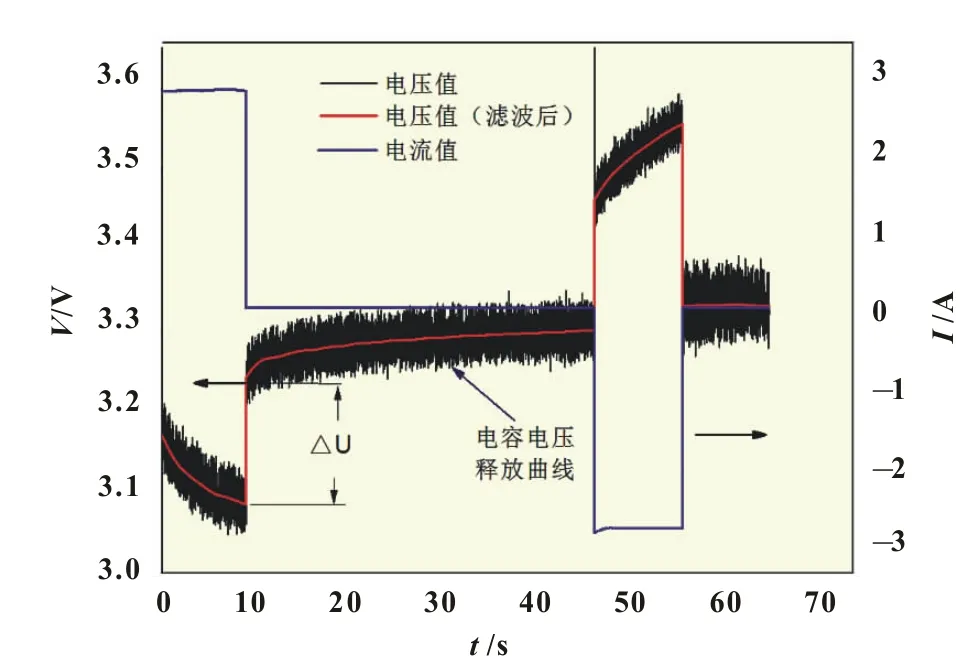
图3　HPPC TEST实验曲线

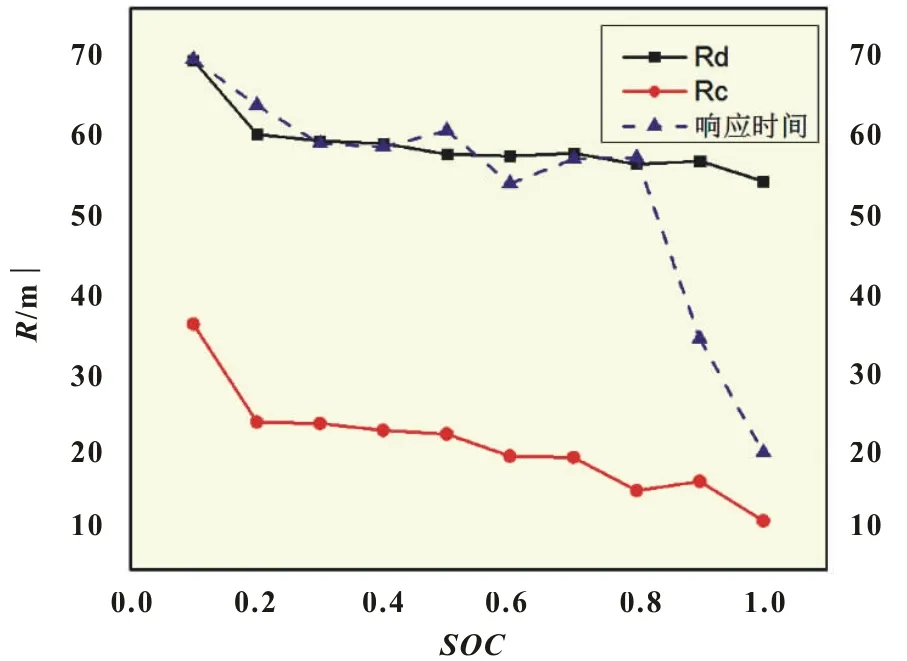
图4　电池模型特征值

2　磷酸铁锂电池SOC估计算法

2.1卡尔曼滤波算法

卡尔曼滤波是以最小均方差为估计的最佳准则，来寻求一套递推估计的算法，其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值[8]。

针对电池SOC测量系统中的非线性模型，文献[9-11]首次提出了一种基于扩展卡尔曼滤波方法。把非线性模型中的非线性函数通过泰勒公式展开成线性模型，再结合卡尔曼的基本滤波方程来进行SOC的估算。基于扩展卡尔曼滤波公式的锂电池SOC估计如式(1)～(6)。式中：Δt为系统采样周期；C为电池标定容量；τ(k)、Rc(k)分别为电池响应时间、极化电阻，其值由图X模型公式查表得出；Up为电池电容电压。

系统状态模型：

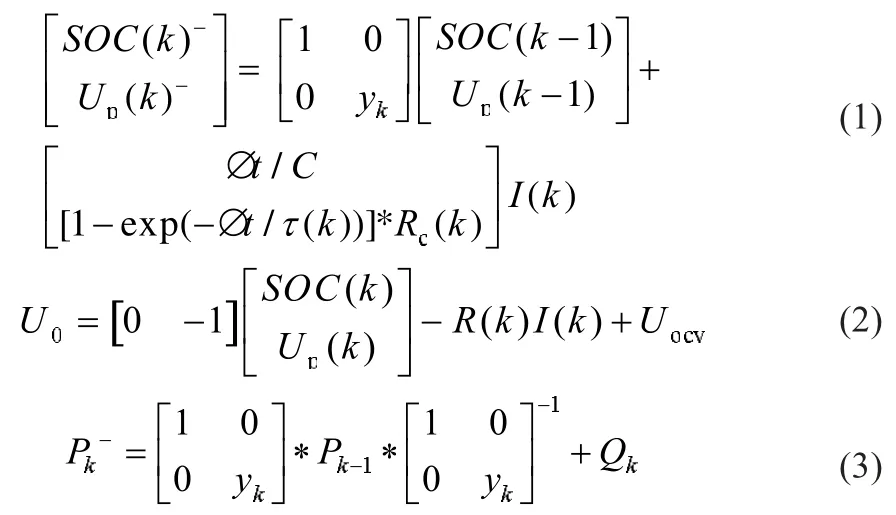
卡尔曼增益系数Kk计算公式，其中Hk取决于SOC和OCV的关系曲线：

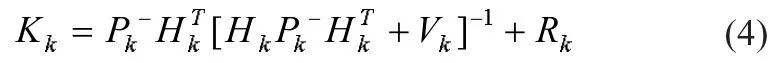
最优估计值及其置信系数：

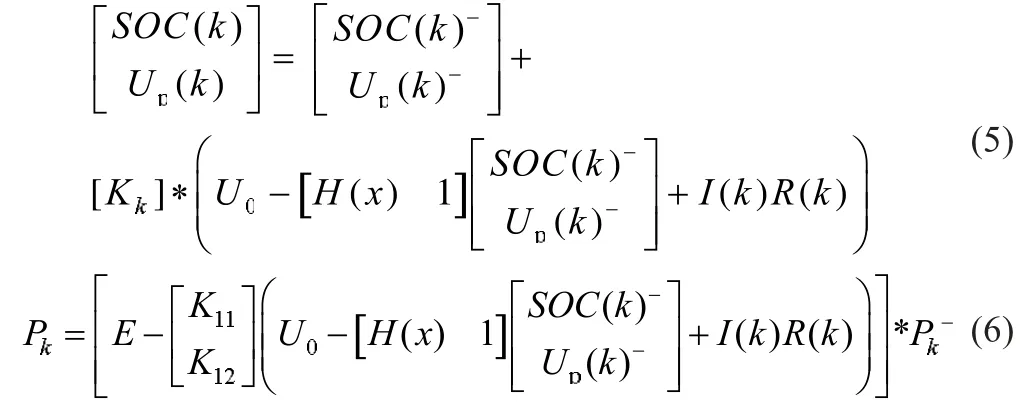
2.2电池放电特征值提取

图5为LiFePO4电池组实际工况下从满电到放完电的一次完整运行过程的单体电压曲线。

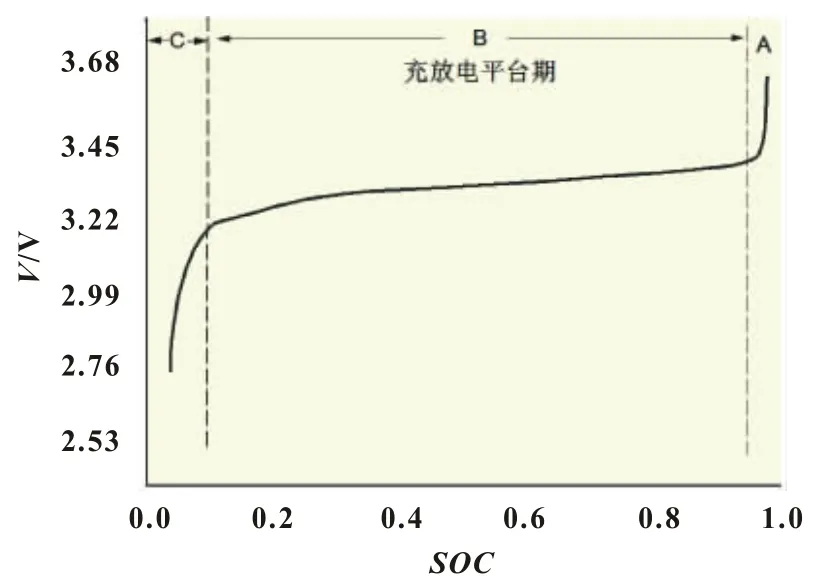
图5LiFePO4电池OCV曲线

电池OCV曲线可分为3个部分，在A区域内，电池充电时电压快速上升直到电池管理系统进入保护模式,而放电时可以很快进入电压平台期(B阶段)。随着电池充电量减少，电池OCV曲线进入B区域(约为SOC95%到15%之间)，在该区域内,电池电压的变化非常缓慢,此时电池处于稳定的工作状态。随着电池SOC的继续降低，电池OCV曲线进入C区域内,充、放电时电池的电压变化较快,属于充电预充区间和放电保护区间。

3　改进扩展卡尔曼滤波SOC算法

在锂电池组的SOC估计系统中，其核心目标是使SOC估计能够实时动态地反映真实的锂电池荷电状态的变化，同时也能具有误差矫正的功能。公式(3)中Kk是卡尔曼增益，代表对上一时刻状态值的协方差系数；Rk为测量噪声的协方差系数。Rk、Pk、Hk等系统参数值决定了系统最终稳态误差，以及系统收敛速度等。

普通EKF算法中，Rk值是由系统测量系统决定的。但在SOC测量中，由于模型本身的误差、系统测量误差等，以及电池本身的不一致性，使用静态的系统误差测置信参数Rk(公式3)的扩展卡尔曼滤波算法反而达不到良好的效果。其原因分析如下：

(1)SOC估计系统特性的数学模型不准确。扩展卡尔曼滤波器估计电池状态，是把非线性的电池状态空间模型进行线性化处理后的计算，期间忽略了非线性系统线性化所导致的误差。

(2)缺乏对噪声模型的完整了解，导致噪声统计特性描述不准确。这一问题对电池系统尤为明显，磷酸铁锂电池本身特性决定其在SOC 95%～SOC 20%的区间内，电压变化极小，相对应的测量噪声对SOC估计影响增大，由于物理原因所导致的噪声模型错误，会对SOC估计结果产生极大影响

(3)应用卡尔曼滤波器时，必须掌握所研究动态系统的数学模型和系统中有关噪声的统计特性。这一点，在实际应用中很难满足。

当电池工作在复杂工况，负载电流变化快，电压波动明显时，此时模型计算的OCV值误差较大，SOC估计值容易出现较大误差。

图6为改进EKF算法的流程图。

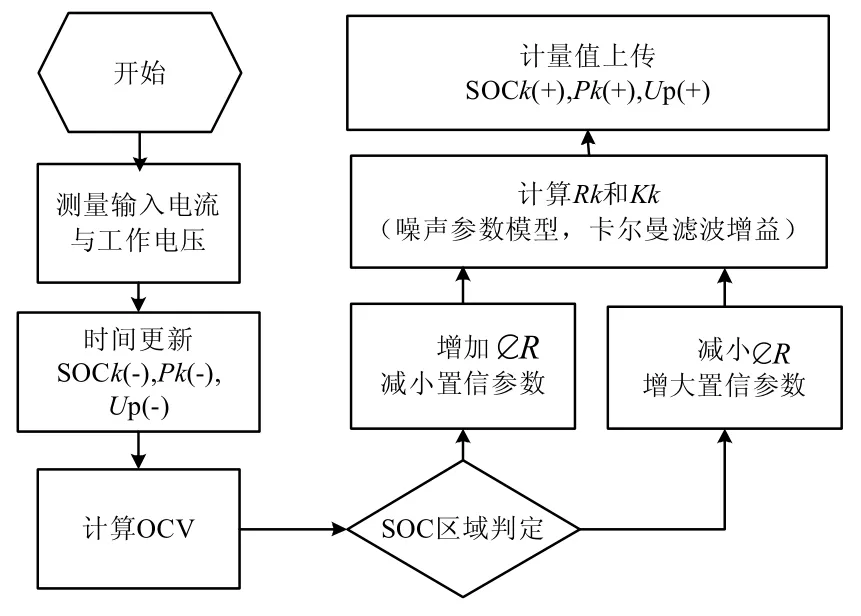
图6　Rk补偿扩展卡尔曼滤波算法流程

在EKF算法中，使用较大的Rk0系数，SOC估计值能很快逼近SOC真值，但是同时SOC容易受到电压测量值和模型误差的影响，其值波动也较大。相反，较大的Rk1有更好的稳态误差值，但达到稳态值需要花费更多的时间，同时，算法对电池和SOC初值误差的矫正表现也较差。从实际运用电池的角度来说，两种结果都不能满足系统要求。

假设系统是带未知模型误差的系统，即真实系统不是式(1)而是：

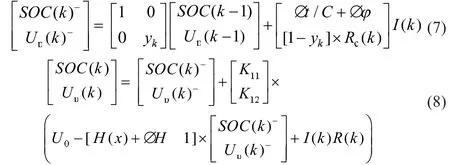
式中：Δφ为状态转移矩阵误差；ΔH为系统模型误差。由于其值均未知，对带模型误差系统进行常规卡尔曼滤波很难达到良好效果。为了补偿模型误差，将真实系统改写为：

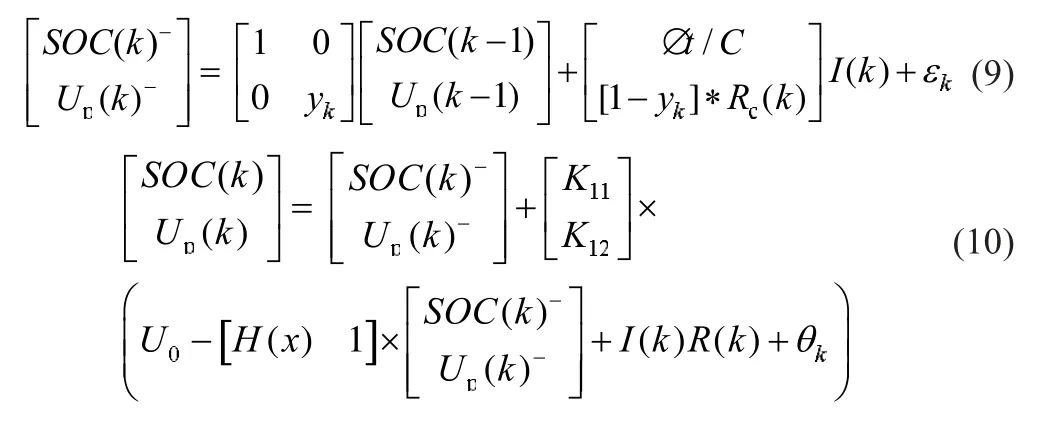
式中：εk为虚拟模型噪声；θk为虚拟量测噪声。可近似假设虚拟噪声εk和θk是带未知时变噪声统计的互相独立的白噪声。对于电池SOC系统，虚拟量测噪声的影响远大于虚拟模拟噪声。

为解决此问题，本文根据电池所在SOC不同的特征区域，把电池SOC分为3个阶段，分别进行不同的Rk补偿。

把公式(4)改写为：

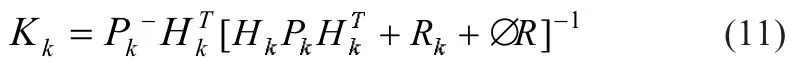
式中：ΔR是针对虚拟噪声的补偿。

在SOC曲线的A区域与C区域，此时SOC随电压变化较快，电压值作为系统估计参数能够有良好效果，系统噪声带来的误差影响较小。此时对系统使用较小的系数，能够有效解决SOC初值误差，并使快速收敛。在B区域(SOC10%～85%)，系统动态补偿ΔR值，减小系统受到电池端电压的影响，使SOC估计不会随电池工作的加载与卸载急剧变化，提高系统的估计精度。对Rk的补偿有助于提高系统收敛速度和鲁棒性，能更好地反应不同工况下的SOC估计值。

4Rk补偿算法验证及结果分析

本文在MATLAB环境下建立电池系统仿真，测试所提出的Rk补偿扩展卡尔曼滤波算法。该仿真系统使用UDDS(美国机车城市工况运行标准)工况模型，其模拟了电动机车在城市内运行时的复杂负载情况，相较于恒定电流负载，对系统动态响应能力要求更高，能够验证卡尔曼滤波的效果。图7为电池测量电压曲线以及卡尔曼算法计算中，滤去负载电流影响后计算出的电池开路电压和所对应的负载电流曲线。

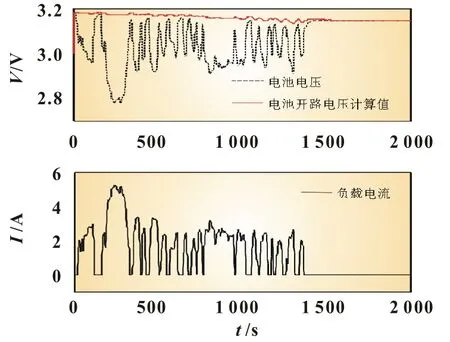
图7　UDDS TEST电流电压曲线

为验证SOC估计值最终的结果，图8表示相同的系统模型工作在不同的Rk值下的SOC曲线，此时SOC初值设置为0.8。图8(b)中可见，Rk参数较大时，系统的跟随性能更好，稳定误差ess=0.7%。Rk参数较小时SOC值受负载电流工况影响较大，其最大误差达到15%，同时也更容易受到采集过程中的噪声因素影响，最终稳定误差ess=2.5%。在Rk可变卡尔曼滤波算法中，系统最大误差只有4%，最终稳定误差ess=0.8%，满足SOC测量的要求。表1显示了三种算法下的误差最大偏差与均方差值，可以看出动态Rk算法具有最优越的性能。

图9为电池测量电压值与卡尔曼滤波算法中的计算电压值的对比。可以看出，卡尔曼估计系统所计算的电压值与实际测量电压值误差主要在电压值有突变的动态情况下，其值差距最大值只有0.01 V。单纯的增加Rk值，可以减少系统受到的误差和波动影响，但是会影响系统的反馈速率。

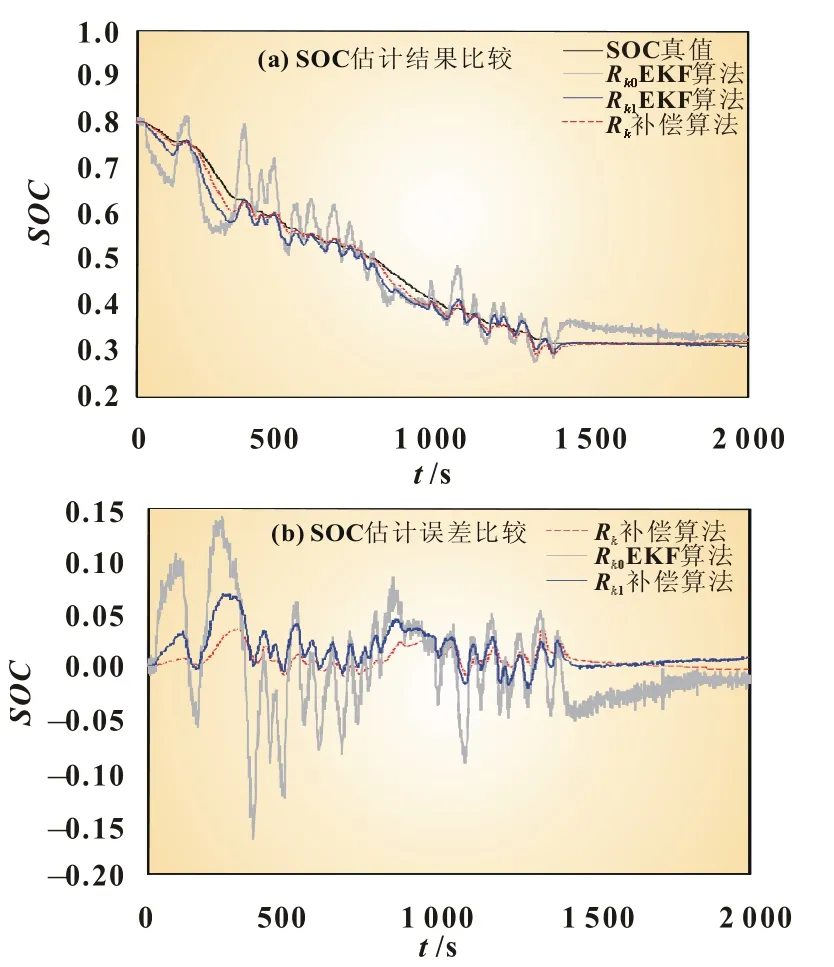
图8　SOC估计曲线(设置正确初值条件)

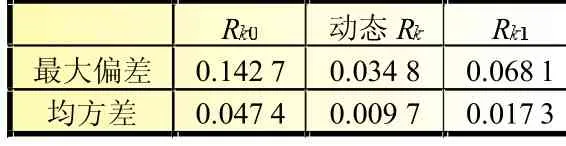
表1　SOC估计误差比较

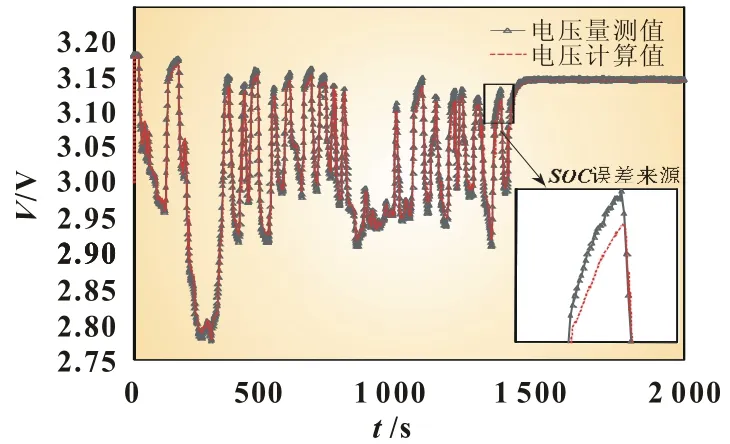
图9　SOC估计曲线(设置正确初值条件)

为了验证算法对SOC的矫正功能，图10为设置系统SOC初值真值为0.8，卡尔曼滤波算法初值设置为0.9的仿真结果。

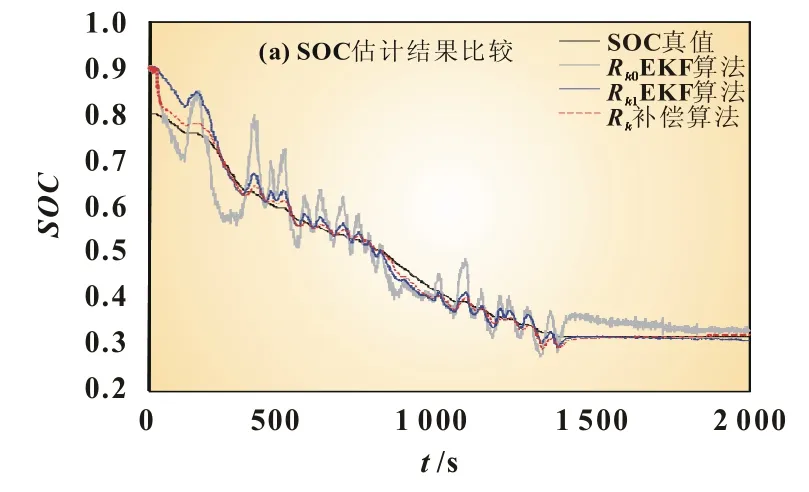
从图10(a)中可见Rk值较小的曲线能迅速调整到真实值附近，但是在SOC平台期(B区域)，LiFePO4电池开路电压相对SOC的变化率极小，无法通过电压反馈实现SOC的精确校准,反而出现了SOC过调整，且最终稳定误差ess=3.5%；相反Rk值较大的算法，均方根误差较大，需要花费更多的时间才能跟随真值。Rk补偿卡尔曼滤波算法在平台期Rk值接近Rk0，因此有良好的接近效果，SOC末端时其值接近Rk1，系统达到了良好的收敛性能与矫正能力，能满足实际系统的需求。

在实际测试中，实验测试数据显示在电池平台期，SOC每变化10%，实际OCV变化只有5 mV，其动态特性难以真正描述，加上系统测量误差、传递误差等。根据电池的不同状态，进行系统参数补偿是十分有必要的。

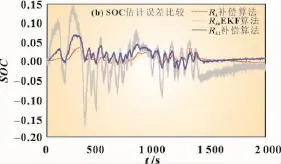
图10　SOC估计曲线(设置错误初值条件)

5　结论

LiFePO4动力电池组SOC的精确估计受诸多因素的影响(温度、工作状态等)，且电池本身具有强烈的非线性与不一致性，其理论模型与实际模型具有一定的误差，利用单一的估计参数难以同时满足SOC估计的精确性与实时性的需求，在初值有误差的极端情况下甚至会导致系统发散。

本文在融合电池组信息的基础上结合EKF滤波算法，将LiFePO4电池组放电过程划分为不同状态，在不同的系统条件下补偿系统Rk值，对SOC进行估计计算。通过使用实际复杂工况下的运行数据进行MATLAB环境下的仿真实验，提高了在负载电流急剧变化的情况下SOC算法的可靠性，同时验证了该算法在SOC系统具有初值误差时，能有效收敛到真值区间，实现SOC的矫正功能。与此同时，本文所使用的模型只能在一定程度上反应其特性。如何更多的融合外部信息，提高LiFePO4电池组SOC估计的精度有待进一步研究。

[1]NG K S,MOO C S,CHEN Y P,et al.Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithiumion batteries[J].Applied Energy,2009,86(9):1506-1511.

[2]PILLER S,PERRIN M,JOSSEN A.Methods for state-of-charge determination and their applications[J].Journal of Power Sources, 2001,96(1):113-120.

[3]CHARKHGARD M,FARROKHI M.State-of-charge estimation for lithium-ion batteries using neural networks and EKF[J].IEEE Transactions on Industrial Electronics,2010,57(12):4178-4187.

[4]尹安东,张万兴,赵韩,等.基于神经网络的磷酸铁锂电池SOC预测研究[J].电子测量与仪器学报,2011,25(5):433-437.

[5]何耀,刘兴涛,陈宗海.基于信息融合的LiFePO4动力电池组SOC估计[J].控制与决策，2014(1):188-192.

[6]刘和平,许巧巧,胡银全,等.自适应卡尔曼滤波法磷酸铁锂动力电池剩余容量估计[J].重大学报,2014,37(1):68-74.

[7]SALAMEH Z M,CASACCA M A,LYNCH W A.A mathematical model for lead-acid batteries[J].IEEE Transactions on Energy Conversion,1992,7(1):93-98.

[8]KALMAN R E.A new approach to linear filtering and prediction problems[J].Journal of Basic Engineering,1960,82(1):35-45.

[9]PLETT G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs:Part 1.Background[J]. Journal of Power Sources,2004,134(2):252-261.

[10]PLETT G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs:Part 2.Modeling and identification[J].Journal of Power Sources,2004,134(2):262-276. [11]PLETT G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs:Part 3.State and parameter estimation[J].Journal of Power Sources,2004,134(2):277-292.

State of charge estimation using extended Kalman filter for battery management systems based on battery model

DENG Gong-tai1,MA Lei1,JIA Jun-bo2,HAN Ming2
(1.School of Electrical Engineering,Southwest Jiaotong University,Chengdu Sichuan 610031,China; 2.Clean Energy Research Center,Temasek Polytechnic,Singapore 529757)

Aiming at the inaccuracy problem of state-of-charge(SOC)estimation under complex conditions,a new SOC estimation algorithm based on EKF(extend Kalman filter)was proposed for LiFePO4high-power batteries.This algorithm carried out feature extraction and pattern classification of the charge and discharge processes,and then re-optimized the estimation model according to different patterns.The new algorithm switched to the matching estimation model to acquire better performance based on the feature matching.The result of simulation with the running data of LiFePO4batteries shows feasibility and effectiveness of the SOC estimation based on the proposed algorithm.

LiFePO4batteries;state-of-charge;energy management;EKF

TM 912.9

A

1002-087 X(2016)10-1931-05

2016-03-14

国家自然科学基金(51177138)

邓宫泰(1988—)，男，四川省人，硕士研究生，主要研究方向为新能源系统。