考虑剪切变形的波形钢腹板组合梁的挠度计算
左志鹏(南昌市城市规划设计研究总院,南昌 330038)
考虑剪切变形的波形钢腹板组合梁的挠度计算
左志鹏
(南昌市城市规划设计研究总院,南昌 330038)
采用能量变分法,建立了考虑剪切变形影响时波形钢腹板组合梁的挠曲线微分方程。利用此挠曲线微分方程,得到了简支波形钢腹板组合梁在不同荷载作用下由剪切变形产生的跨中挠度的计算公式。通过与空间有限元模型进行对比分析,表明理论计算公式是准确的。
波形钢腹板组合梁;剪切变形;跨中挠度;理论计算公式
【DOI】10.13616/j.cnki.gcjsysj.2016.11.003
1 引言
为减轻混凝土主梁结构的重量从而减小永久荷载作用下结构的内力,桥梁工程师们做了一系列创新而有益的探索,在20世纪80年代末,波形钢腹板组合梁桥作为一种新型组合结构桥梁应运而生[1]。波形钢腹板组合梁桥中利用很薄的波形钢腹板替代厚度很大的混凝土腹板后,与传统混凝土梁桥相比,可提高预应力使用效率、降低造价、节约成本等,并且从根本上解决了混凝土腹板的开裂问题。近年来,国内外学者通过理论计算、有限元和试验等多种手段对波形钢腹板梁抗剪、弯曲和扭转等方面的性能进行了大量深入的研究[2,3],得到了一些有益的结论和有价值的成果。本文对波形钢腹板组合梁的挠度进行了研究,首先分析了波形钢板的刚度特征,依据波形钢腹板组合梁自身的几何特征探讨了在剪切变形的影响下波形钢腹板组合梁变形计算的理论公式。
2 波形钢板的刚度分析
2.1轴向刚度和抗弯刚度
从几何形状特征上看,波形钢板由于具有折皱效应[4],在轴向力作用下沿纵向可以自由变形,因此可以预见其轴向刚度相比于平钢板要弱,也即当组合梁截面承受轴向力和弯矩作用时,可以忽略波形钢腹板的贡献,这一点也已为国内外的研究所证实[5,6]。
对于图1中所示的组合截面,需要计入上、下混凝土板和波形钢腹板钢梁两者提供的刚度,此时截面的轴向刚度和抗弯刚度可分别采用式(1)和式(2)计算:

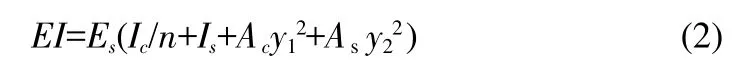
式中,As为上、下钢翼缘板的面积之和;Is为波形钢腹板钢梁的惯性矩;y1为混凝土板形心轴到组合截面形心轴的距离;y2为波形钢腹板钢梁形心轴到组合截面形心轴的距离。
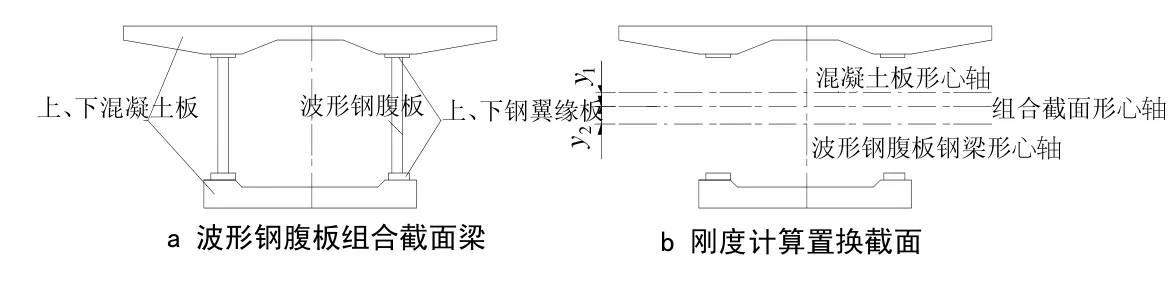
图1 波形钢腹板组合梁截面刚度计算简图
2.2剪切刚度
根据文献[2]的分析研究,波形钢板(见图2)的剪切模量值有所降低(降低10%左右),并得出其有效剪切模量Ge的表达式为:

式中,G为钢的剪切模量。
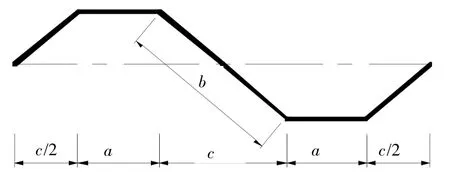
图2 波形钢板示意图
另外,混凝土板所分担的剪力荷载很小,截面上的剪应力基本上等值均匀分布于波形钢腹板之上。因此,截面的剪切刚度计算公式如下:

3 考虑剪切变形的短期刚度及变形计算
选取两个独立的广义位移w(x)(截面挠曲位移)和(截面挠曲转角)以考虑剪切变形的影响。为建立分析方程,根据第2节波形钢腹板组合梁的弯曲特性和剪切特性,可以假定两点:在计算组合梁的弯曲正应变能时,不考虑波形钢腹板的贡献;在计算组合梁的剪切应变能时,只考虑波形钢腹板的贡献。
结构的总势能由三部分组成,即:外荷载势能、组合梁剪切应变能和组合梁弯曲正应变能:

式中:∏p为外荷载势能;∏w为波形钢腹板组合梁剪切应变能;∏f为波形钢腹板组合梁弯曲正应变能。
如图3所示,得出各势能的表达式代入式(5),并根据变分法则,可得:
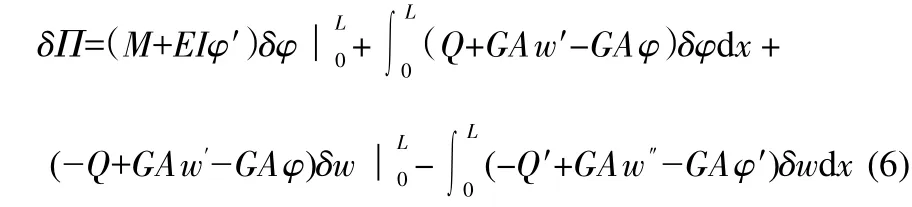
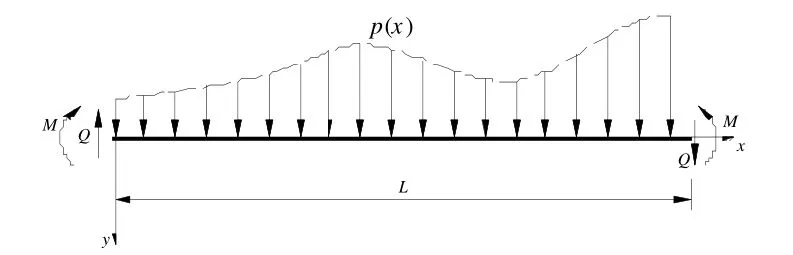
图3 坐标系及荷载
根据最小势能原理δ∏=0,并注意到M'=Q,可得:

式中,抗弯刚度EI可根据式(2)计算,抗剪刚度GA可根据式(4)计算。
根据以上推导的挠曲线微分方程并注意到波形钢腹板组合梁截面上的剪应力基本上等值均匀分布于波形钢腹板上,据此可得波形钢腹板简支梁处于跨中集中荷载、三分点对称集中荷载、均布荷载作用下的总挠度wsb1、wsb2、wsb3分别为:
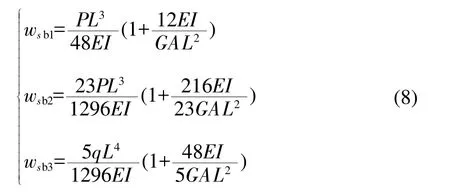
式中,P为集中外荷载总和;q为外荷载集度。
4 有限元验证
以文献[7]的试验梁为对象(见图4)。试验梁跨度为6500mm,计算跨度为6400mm,梁高为540mm;混凝土强度等级为C50,上混凝土板厚度为100mm,下混凝土板厚度为110mm;波形钢腹板钢梁的顶、底钢翼缘板以及钢腹板均采用Q345钢,厚度分别为10mm和4mm;波形钢腹板波长值分别为a=80mm,b=86mm,c=70mm。
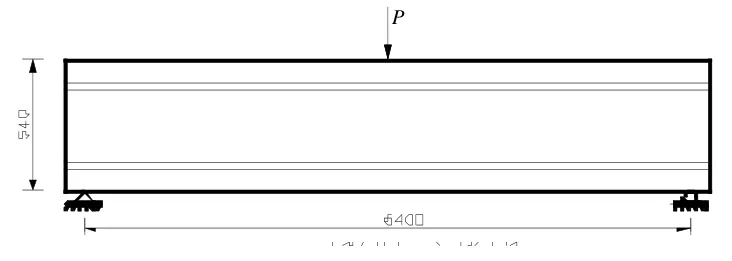
图4 波形钢腹板工字型组合梁构造图
据此,建立空间有限元模型,如图5所示。在有限元模型中,波形钢腹板钢梁选用板单元模拟,混凝土板选用实体单元模拟;不考虑上、下界面的相对滑移即板壳单元的节点和实体单元的节点完全耦合;为模拟边界条件,在固定支座处,约束节点沿纵向、横向和竖向的平动自由度,在活动支座处,约束节点沿竖向的平动自由度;模型梁受到跨中集中荷载作用。

图5 波形钢腹板工字型组合梁空间有限元模型
根据文献[7]的试验,试验梁跨中位移一直到8-9mm左右时,试验梁仍处于线弹性状态。根据有限元模型分析和理论计算,表1列出了梁在线弹性范围内的跨中挠度值。表1中,有限元分析值和理论计算值相差在7%左右,由此可见,理论计算公式有较好的精度。需要说明的是,本节计算抗弯刚度时考虑了上、下钢翼缘板的贡献,即采用式(2)。

表1 简支波形钢腹板组合梁的跨中挠度
此外值得注意的是,该试验梁的高跨比大约为1/10,剪切变形引起的挠度占总挠度的百分比达到了22%,可见高跨比是影响波形钢腹板组合梁剪切变形重要的因素之一。
为了研究高跨比的影响,在跨中集中荷载P=10kN和截面不变的情况下,通过改变梁的跨径,给出了模型梁在不同高跨比下的跨中挠度,见表2。由表2,当高跨比由1/10变化到1/30时,组合梁由剪切变形引起的跨中挠度占总挠度的百分比从28%减小到4%,即随着高跨比的降低,剪切变形对挠度的影响也随之降低。
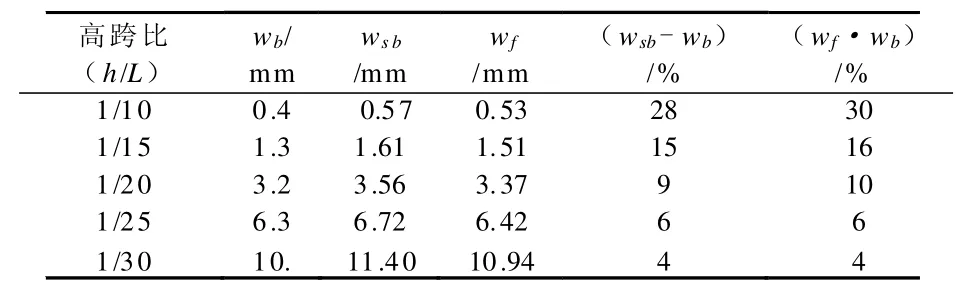
表2 不同高跨比时简支波形钢腹板组合梁的跨中挠度
5 结语
本文考虑剪切变形对挠度的贡献,得到了波形钢腹板简支组合梁分别在跨中集中荷载、三分点对称集中荷载和均布荷载作用下短期跨中挠度的计算公式,并通过空间有限元模型进行了验证,表明理论计算公式具有较好的精度。此外,通过有限元和理论计算分析可知,高跨比是影响波形钢腹板组合梁剪切变形重要的因素之一。
【1】CheyrezyM,CombaultJ.Compositebridgesw ithcorrugatedsteel webs-Achievementsandprospects[C].IABSESymposium,Brussels, 1990:M ixed Structures,includingNew Materials,IABSEReports,1990.
【2】JohnsonRP,Cafolla J,BERNARDC.Corrugatedwebsinplategirders forbridges[J].Proceedingsofthe ICE-StructuresandBuildings,1997, 122(2):157-164.
【3】李宏江.波形钢腹板箱梁扭转与畸变的试验研究与分析[D].南京:东南大学,2003.
【4】刘磊,钱冬生.波纹钢腹板的受力行为[J].铁道学报,2000,22(B05): 53-56.
【5】ElgaalyM,SeshadriA.Girderswithcorrugated webs under partial compressiveedge loading[J].JournalofStructuralEngineering,1997, 123(6):783-791.
【6】吴文清.波形钢腹板组合箱梁剪力滞效应问题研究[D].南京:东南大学,2002.
【7】陈卓异,黄侨,杨明.波形钢腹板预弯工形梁的试验研究[J].东南大学学报:自然科学版,2013,43(5):973-978.
Calculation of Deflection for Composite Beams w ith CorrugatedSteel Webs Considering Shear Deformation
ZUO Zhi-peng
(NanchangUrbanPlanning&Design Institute,Nanchang330038,China)
Considering the influenceof the shear deformation,the deflection differential equation ofstringof the compositebeam bridgew ith corrugatedsteelwebsisestablishedbyenergyvariationalmethod.Therefore,having thedeflectiondifferentialequationof string,a calculation formula ofmid-span deflection which iscaused by shear deformation,and the short-term reduced rigidity of the simplysupported compositebeam bridgewithcorrugatedsteelwebsunderdifferentloads,areprovided.Comparedw ith thespace finite elementmodel,itshowsthatthetheoreticalformulaisaccurate.
compositegirderwithcorrugatedsteelweb;sheardeformation;m id-spandeflection;theoreticalcalculation formula
U448.21+6
B
1007-9467(2016)11-0025-03
左志鹏(1991~),男,江西抚州人,助理工程师,从事现代桥式与桥梁结构设计理论研究。
2016-05-27

