加速寿命试验失效时间的估算方法研究
王耀冬, 俞卫博, 宣兆龙, 姚 恺, 李天鹏
(军械工程学院,河北 石家庄 050003)
加速寿命试验失效时间的估算方法研究
王耀冬, 俞卫博, 宣兆龙, 姚 恺, 李天鹏
(军械工程学院,河北 石家庄 050003)
在加速寿命试验失效时间估算的原有方法基础上,从概念对称角度出发,提出了区间中位分布估计法和指数均匀分布估计法。通过理论计算分析和蒙特卡洛模拟分析两方面,对比和检验了每种估算方法的特点和准确性。结果表明,提出的方法较原方法在特定条件下具有一定的优越性,当产品的失效率为递增型时采用指数均匀分布估计法、递减型采用对数均匀分布估计法或是变化未知时使用等间隔分布估计法和区间中位分布估计法,所得的失效时间估计精度较高。因此,在对加速寿命试验失效时间进行估算时,应视产品的失效类型选择估算方法,以提高参数估计的准确性。
加速寿命试验; 失效时间; 估算方法; 蒙特卡洛
1 引 言
加速寿命试验是指在不改变失效机理的前提下,对产品加载高于正常条件下的应力水平,检测并记录产品的失效时间等失效数据,最后用统计方法对这些数据进行处理,从而获得产品正常条件下的各项可靠性指标的方法[1]。从中可以看到,若确定的产品失效时间存在偏差,那么所得的各项可靠性指标也必然存在偏差。为了避免这种情况,在整个加速寿命试验过程中应采用自动监测、连续检测的方法。但现阶段仅对于试验样品所处的环境应力能够实现自动监测,连续检测不仅在技术上要求高,而且费用昂贵,耗费人力物力。因此,实际应用中通常采用周期检测的方法[2],即将试验时间分为若干个检测区间,在每个区间的端点对样品进行检测,并记录失效数据。但是,这种方法只能得到检测区间内样品的失效个数以及失效的发现时间,而无法得到每个失效样品真正的失效时间。因此,仍需对获得的失效数据进行估计,以获取准确有效的失效时间。
2 失效时间的估算方法
失效时间的估算其实就是对失效时间在检测区间内的再分布,文献[3]中使用了等间隔分布估计法,文献[4]中又介绍了对数均匀分布估计法,这两种为加速寿命试验中常用的失效时间估算方法。而既然是失效时间的再分布,在对比了两种常用方法的形式后,由概念对称角度出发自然提出了两种新的估算方法,即区间中位分布估计法和指数均匀分布估计法。
假设在检测区间[tj-1,tj]时间内,测得样品失效数为rj,估算此间隔内第k个失效样品的失效时间tjk。
2.1 等间隔分布估计法
将rj个样品的失效时间均匀分布在[tj-1,tj]内,计算公式如下
(1)
2.2 对数均匀分布估计法
将rj个样品的失效时间的对数均匀分布在[lntj-1,lntj]内,计算公式如下
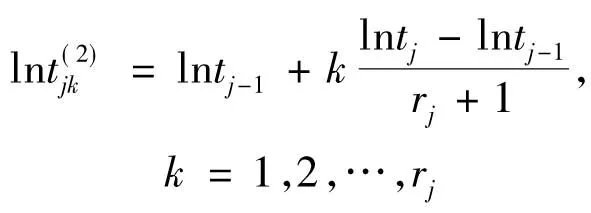
(2)
2.3 区间中位分布估计法
将检测区间[tj-1,tj]均匀分成rj个子区间,则每个样品的失效时间位于该子区间的中点,计算公式如下
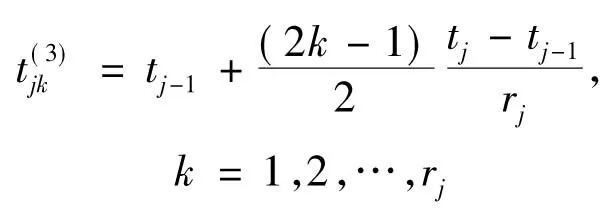
(3)
2.4 指数均匀分布估计法
将rj个样品的失效时间的指数均匀分布在[exptj-1,exptj]内,计算公式如下
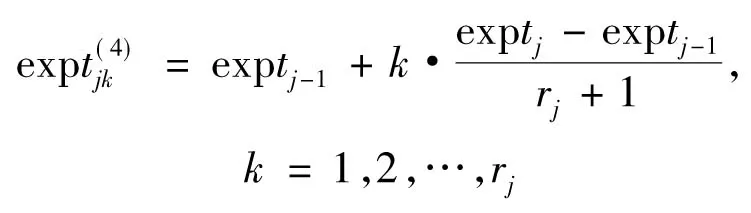
(4)
3 估算方法对比
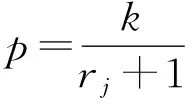
3.1 等间隔分布估计法与对数均匀分布估计法
由(1)式和(2)式可得
(5)

F(x)=(1-p)x-p+px1-p
(6)
对F(x)求一阶导数

(7)
3.2 等间隔分布估计法与区间中位分布估计法
由(1)式和(3)式可得
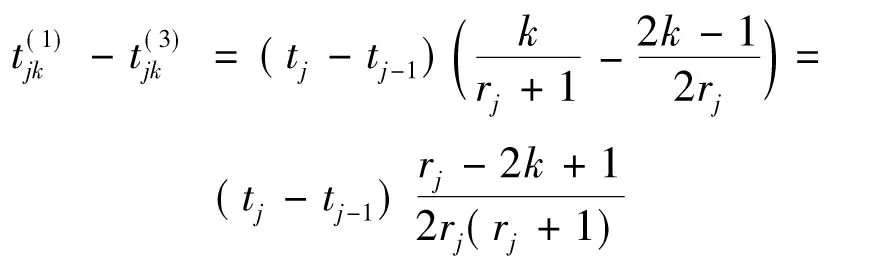
(8)

3.3 等间隔分布估计法与指数均匀分布估计法
由(1)式和(4)式可得
(9)
令x=tj-tj-1,则
F(x)=(1-p)exp(-px)+pexp[(1-p)x]
(10)
对F(x)求一阶导数
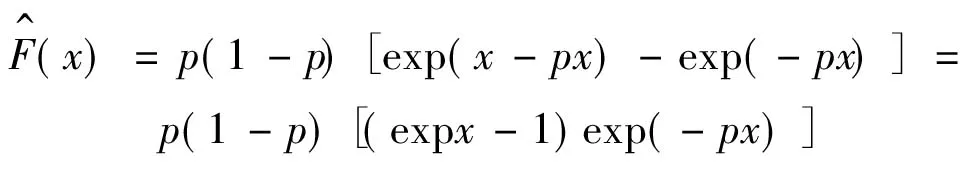
(11)

3.4 对比分析
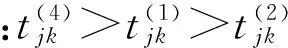
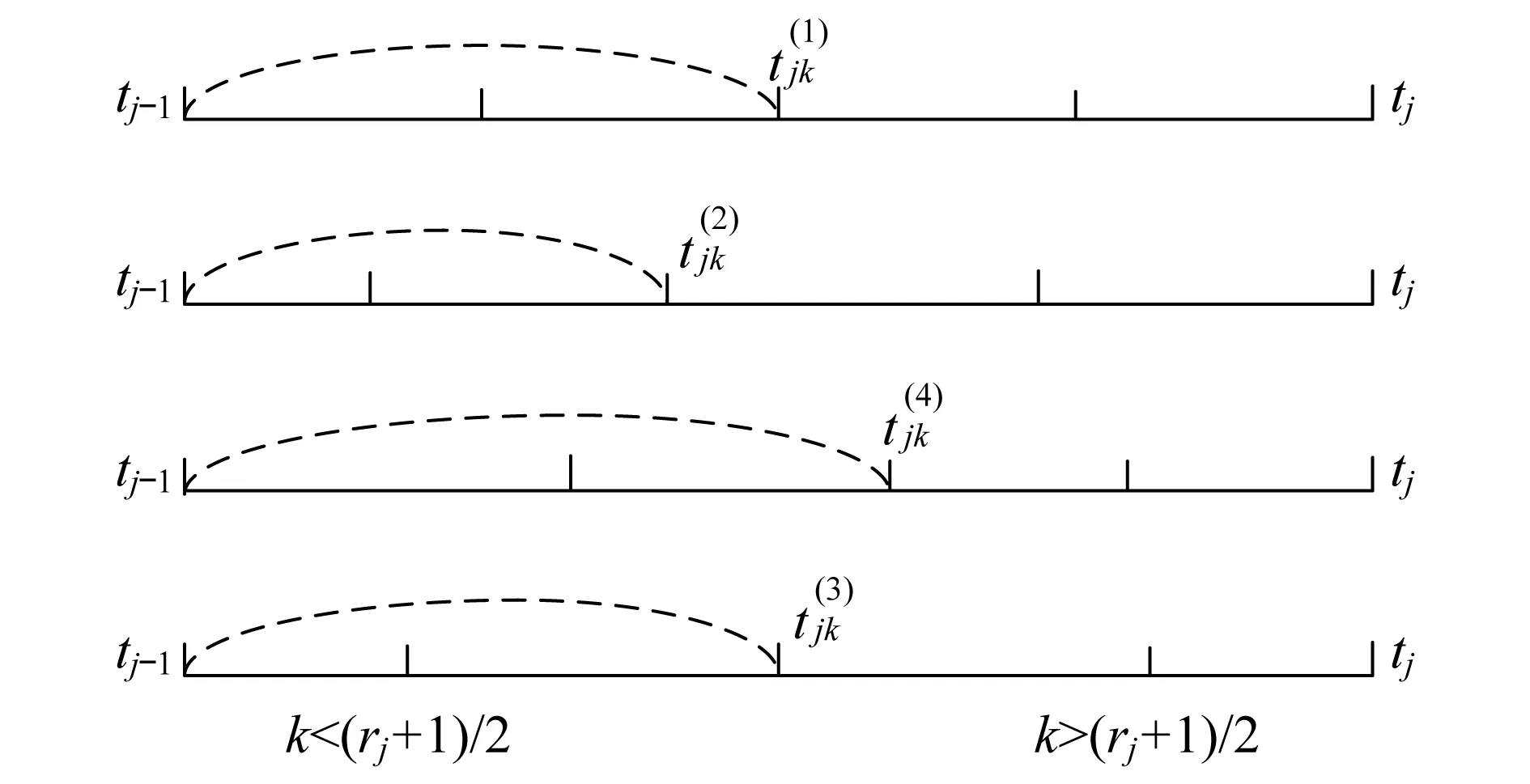
图1 四种失效时间估算方法对比Fig.1Comparison of four methods of failure time estimation
即与等间隔分布估计法相比,对数均匀分布估计法估算出来的失效时间先密后疏,适合那些失效率随时间递减的产品;指数均匀分布估计法估算出来的失效时间先疏后密,适合那些失效率随时间递增的产品;而区间中位分布估计法估算出来的失效时间,分别在k=(rj+1)/2两侧先疏后密,适合失效率为“浴盆曲线”,即经历早期失效、偶然失效和耗损失效阶段的产品。
4 实例分析
使用蒙特卡洛法[5]进行随机变量抽样,得到模拟试验数据,然后分别用以上四种方法进行失效时间估计,并进一步得到可靠性参数估计。比较四种失效时间估算方法得到的可靠性参数,说明每种方法的精度和特点。
Weibull分布是可靠性中常用的一种寿命分布[6],在拟合随机数据时有很大的灵活性和适应性[7]。双参数Weibull 分布的分布函数和密度函数分别为
F(t)=1-exp[-(t/η)m],t≥0
(12)
f(t)=(m/ηm)tm-1exp[(t/η)m],t≥0
(13)
式中:m为形状参数,m> 0;η为特征寿命,η>0。
则Weibull 分布的失效率函数为
(14)
可以看到,λ(t)是时间t的幂函数,当m> 1时,λ(t)是增函数,失效率随时间递增;当m<1时,λ(t)是减函数,失效率随时间递减;当m= 1时,λ(t)是常数,失效率恒定,可视为指数分布。因此,可以根据m的数值区分不同的失效类型。
设容量为rj的全子样数据为t1 (15) 似然方程为 整理化简后得 (16) (17) 令η=100,分别取m1=0.6、m2=1、m3=2,通过蒙特卡洛模拟得到三种失效类型的Weibull分布随机变量共三组,再将每组随机变量代入上述四种失效时间估算方法中,分别得到检测区间[tj-1,tj]上的四组容量为rj的全子样数据t1,t2,…,trj,即估算后的失效时间tjk。将tjk代入上述参数估计的方法中,由(17)式用迭代法[8]求出m的极大似然估计,再由(16)式得到η的极大似然估计。经过大量的模拟,将得到的m和η的估计值取平均值,具体数值如表1所示。 由表可以看出,当m<1时,对数均匀分布估计法得到的结果与真值最为接近,指数均匀分布估计法误差最大;当m=1时,等间隔分布估计法和区间中位分布估计法得到的结果与真值较为接近;当m>1时,指数均匀分布估计法得到的结果与真值最为接近,对数均匀分布估计法误差最大。 表1 参数的极大似然估计Tab.1 Maximum likelihood estimation of parameters 通过理论计算分析和蒙特卡洛模拟分析两方面,对比并检验了四种方法的准确性。结果表明,在对失效时间进行估算时,应视产品的失效类型选择估算方法。若产品的失效率为递增型,则采用指数均匀分布估计法得到的结果精度较高;若产品的失效率为递减型,则采用对数均匀分布估计法得到的结果精度较高;若产品的失效率变化未知,则采用等间隔分布估计法和区间中位分布估计法得到的结果精度较高。为加速寿命试验统计分析中对失效时间的估计,提供了方法和思路,提高了参数估计的准确性。 [1] 陈循,张春华,汪亚顺,等.加速寿命试验技术与应用[M].北京:国防工业出版社,2013. CHEN Xun,ZHANG Chunhua,WANG Yashun,et al.Accelerated Life Testing Technology and Application[M].Beijing:National Defense Industry Press,2013. [2] 张春华.步降应力加速寿命试验的理论和方法[D].国防科学技术大学,2003. ZHANG Chunhua.Theory and Method of Step-谦down-谦stress Accelerated Life Testing[D].National University of Defense Technology,2003. [3] GJB736.13-91.火工品试验方法 加速寿命试验 恒定温度应力试验法[S]. GJB736.13-91.The test sensitivity method.Accelerated Life Test.Constant temperature stress test method[S]. [4] 茆诗松,王玲玲.加速寿命试验[M].北京:科学出版社,1997. MAO Shisong,WANG Lingling.Accelerated Life Test[M].Beijing:Science Press,1997. [5] 张德丰,周燕.详解MATLAB在统计与工程数据分析中的应用[M].北京:电子工业出版社,2010. ZHANG Defeng,ZHOU Yan.The application of MATLAB in statistics and engineering data analysis[M].Beijing:Electronic Industry Press,2010. [6] Saad J.Almalki,Saralees Nadarajah.Modifications of the Weibull distribution:A review[J].Reliability Engineering & System Safety,2014,124(9):32-55. [7] 熊华锋.复合材料疲劳分散性与强度分散性的关系[D].南京航空航天大学,2009. XIONG Huafeng.A Relationship of Dispersity between Fatigue Life and Strength of Composites[D].Nanjing University of Aeronautics and Astronautics,2009. [8] 张军.数值计算[M].北京:清华大学出版社,2008. 王耀冬 男(1991-),黑龙江宾县人,硕士研究生,主要研究方向为弹药系统设计与试验评估。 Research on the Estimation Method of Accelerated Life Test Failure Time WANG Yaodong, YU Weibo, XUAN Zhaolong, YAO Kai, LI Tianpeng (Ordnance Engineering College,Shijiazhuang 050003,China) This paper presents the interval median distribution estimation and exponential uniform distribution estimation,which is based on the original method of estimating the accelerated life test failure time from the conception of symmetry.We examined the characteristics and accuracy of each estimation method by theoretical analysis and Monte Carlo simulation.The results show that the new method has superiority in certain conditions.When the failure rate of the product is increasing,we use the exponential uniform distribution estimation.When the failure rate is decreasing,we use the logarithmic uniform distribution estimation.When the change is unknown,we use the equal interval estimation and interval estimation.These methods have high estimation precision.Therefore,in order to improve the accuracy of parameter estimation,we should choose the estimation method in failure time estimation of accelerated life test depending on products estimating failure types. accelerated life test; failure time; estimation method; Monte Carlo 俞卫博 男(1976-),山西永济人,副教授,主要研究方向为弹药系统设计与试验评估。 TB 114 A

5 结 论



