远火分队机动过程中动态模型研究
王 彬, 黄少罗, 王广彦
(1.军械工程学院 军事教研室;2.军械工程学院 装备指挥与管理系,河北 石家庄 050003)
远火分队机动过程中动态模型研究
王 彬1, 黄少罗1, 王广彦2
(1.军械工程学院 军事教研室;2.军械工程学院 装备指挥与管理系,河北 石家庄 050003)
远火武器系统依托其发射速度快、射程远、火力猛、威慑力大、机动性好、操作方便等特点,越来越受到战场重视。文章分析了国内目前对装备机动过程研究现状,结合远火分队自身机动特点,从六个方面分析了影响远火分队在机动过程中的影响因素,通过模型描述并分析了远火分队在机动过程中的机动速度,到达指定机动位置的坐标以及到达位置的时间,利用数学公式描述其动态机动过程,建立了远火分队机动过程计算流程图,并依据数学模型进行实例分析,通过MATLAB软件仿真得出速度、时间、路程的关系图,并加以分析,研究远火分队的机动过程动态模型对今后研究远火武器系统的战损仿真具有重要借鉴意义。
远火分队; 机动; 动态模型
1 引 言
随着信息化水平的不断提高,传统的阵地作战已逐步向灵活多样的联合机动作战转变。远程火箭炮武器系统作为陆军装备的“杀手锏”武器,依靠发射速度快、射程远、火力猛、威慑力大、机动性好、操作方便等优势,在联合机动作战中扮演着重要角色[1]。目前我国远火分队通常以营或连为基本作战单元,远火武器系统按用途主要分为战斗装备和保障装备两大部分[2]。远火分队在执行任务过程中,无论在作战还是机动过程中,通常都是以“集群”的方式出现。远火武器系统在战场上停留时间较短,更多的时间都在机动过程中,所以研究远火武器系统在机动中的动态过程,对今后研究远火武器系统的战斗损伤有着重要借鉴意义。
当前我国对战斗损伤的研究对象多以静态的、相对位置较为固定的装备为主,忽略了被毁伤装备的机动行为,这与战场实际不相符合。在作战过程中,无论是作为进攻方或防守方,其机动行为是时时存在的。以往研究动态模型的方法有贝叶斯方法[3]、兰彻斯特方程线性规律[4]等研究方法,但并不能直观反映出机动对象的实时状态,特别对于描述类似于远火武器系统等集群装备时,作战指挥员要想实时掌握机动对象的各项动态指标,最直观的方法就是通过图形、图表来给出机动对象的状态过程。本文就以远火分队在机动过程中的影响因素、机动过程的动态模型描述以及计算过程进行阐述。
2 远火分队机动过程的影响因素分析
影响远火分队机动的因素主要有路况地形、天气气候、敌火力干扰等客观因素,也有机动方式、机动能力、机动队形及组织指挥等主观因素。在实际作战环境下,指挥员要具体考虑以下因素:
(1) 地形与路况:如山路、丘陵、等级公路级别,路面损坏程度,道路是否结冰湿滑、是否穿过闹市等人群密集地区等,其修正系数D如表1所示。

表1 地形条件对远火分队机动过程的修正系数值Tab.1The correction coefficient value of terrain conditions on the long-range rocket uint
(2) 天气气候:如降水、降雪、雷、风、雾霾等,其修正系数U如表2所示。

表2 气候条件对远火分队机动过程的修正系数值Tab.2The correction coefficient value of climatic conditions on the long-range rocket uint
(3) 敌火力干扰:如火力压制、烟幕、临时设障等,其修正系数W如表3所示。

表3 敌火力干扰对远火分队机动过程的修正系数值Tab.3The correction coefficient value of the enemy fire disturbance on the long-range rocket uint
(4) 机动方式:如自行机动、乘交通工具机动;
(5) 机动能力:如修路能力、架桥能力、渡河能力、破障能力等;
(6) 机动队形:如同步机动、分批次机动、连续机动、分散机动以及各装备车辆间距等。
以上因素一部分可以用数学表达式进行定量描述,另一部分可以归结为影响系数。作战指挥员要综合考虑机动因素影响,把握机动过程中的首要选取原则,例如从出发地域向作战地域集结时要首要选取时间最短原则,避免贻误战机;而从作战地域撤退时且没有其他作战任务时,就应优先选择道理隐蔽原则,充分利用地形地貌,尽可能在机动撤退的过程中伪装自身。
3 远火分队机动过程动态模型描述
在远火分队机动过程中,认为其运动路线是固定的。如果要考虑运动路线的不确定因素,则应当给出对应的分布函数,并利用其他综合评判方法选出既定路线,本文不予阐述。在远火武器系统机动的动态模型中,主要研究机动速度和空间位移两个重要参数。利用数学公式对其进行分析可以直接给出速度、时间和位移三者之间的关系。
3.1 远火分队的机动速度
机动速度的计算是依靠特定环境条件对标准速度(平均速度)进行修正的结果。假设在某种特定的作战环境和作战任务下,远火分队的标准机动速度为v0,设有n类环境因素,第i类环境有mi个,第i类环境因素对远火分队机动速度的影响系数为α,则:
(1) 第i类单个因素对远火分队机动速度的影响结果为
v=αiv0,0≤αi<1,i=1,2,…,n
(1)
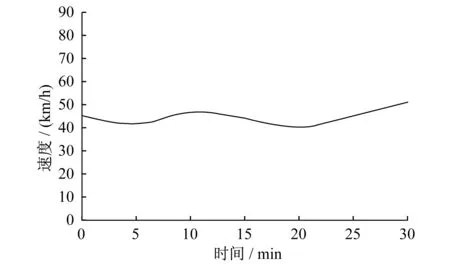
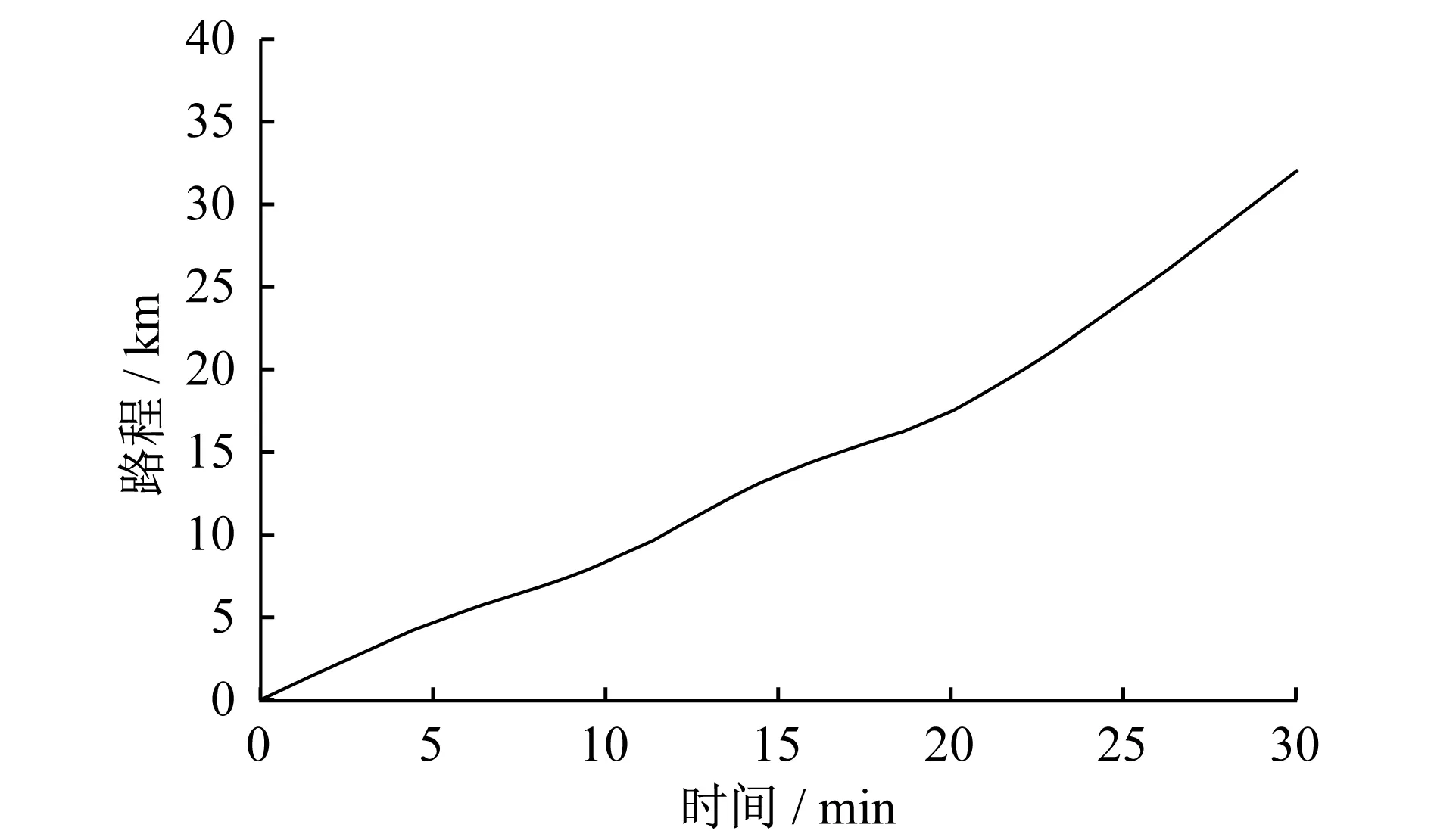
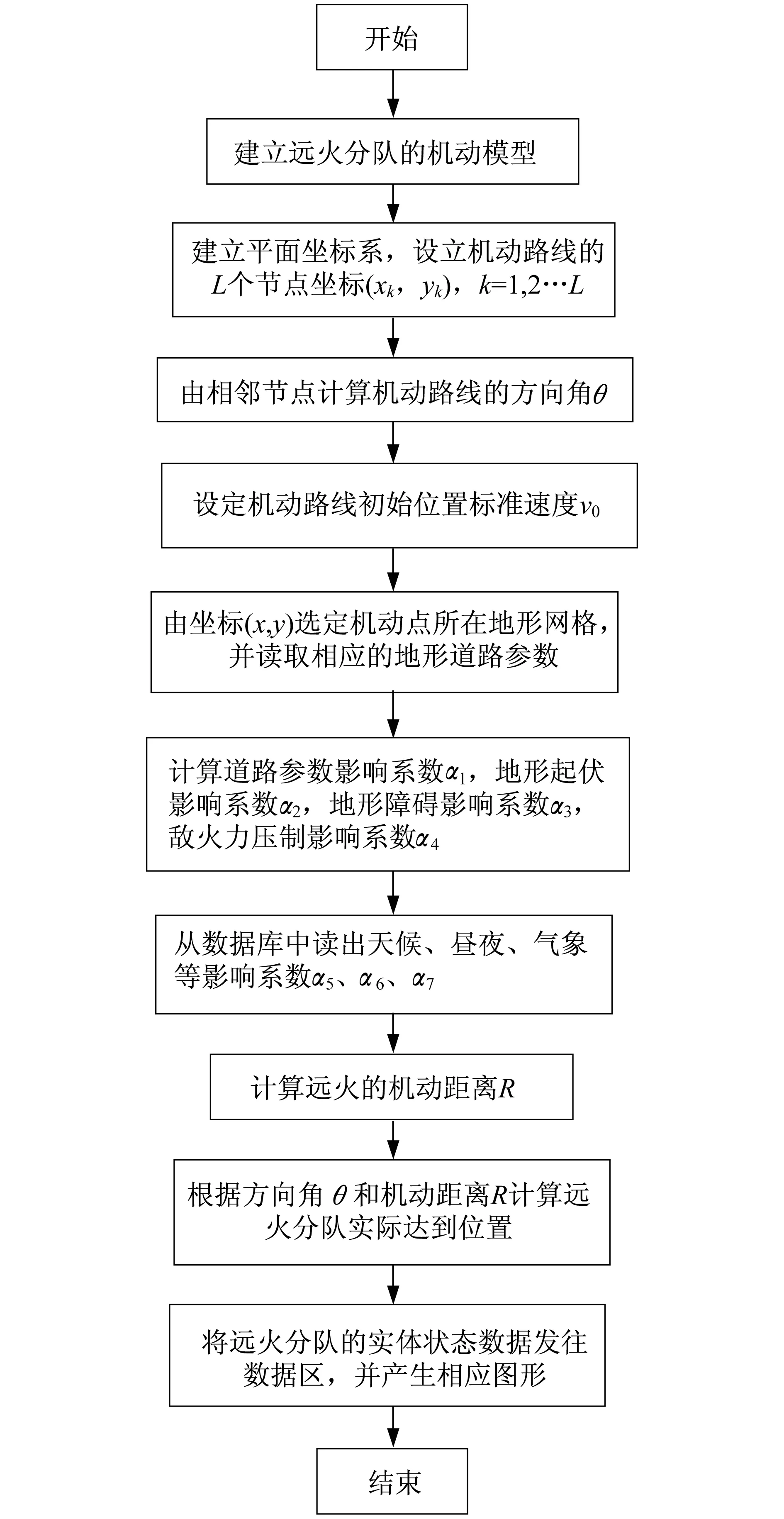
(2) 第i类有j(i)(1 (2) (3) 有s类环境因素,每类都有因素影响远火分队的机动速度,设第i类有j(i)(1 (3) 3.2 远火分队的机动位置坐标和机动到达时刻 (1) 基本计算条件 设远火分队的机动路线是一条折线,有L个节点,坐标为(xk,yk),k=1,2,…,L。其中(x1,y1)为远火分队的起始点坐标,远火分队的机动路线由L-1条线段构成。以下计算公式以第k段机动路线为例,有s(1 ① 如果xk+1=xk且yk+1>yk,则θ=π/2;如果xk+1=xk且yk+1 设机动路线的第k段所对应的环境因素对机动距离的修正系数为βk(0<βk≤1),则远火分队机动路线上第k个节点到第k+1个节点间的距离,可由其平面距离Rk(水平面上投影距离)可表示为 (4) 其中, (2) 到达节点的时间和指定时刻机动位置的坐标 远火分队到达第k+1个节点的时间为 (5) Tk表示远火分队到达第k个节点的时间。 远火分队在T(Tk≤T≤Tk+1)时刻的位置坐标为 (6) (3) 到达指定位置的的时间 由给定条件,也可计算出远火分队到达指定位置(x,y)(xk≤x≤xk+1,yk≤y≤yk+1)的时刻 (7) 3.3 远火机动模型的计算流程 根据节3.1和节3.2的各个计算公式,对远火机动过程进行仿真时,计算流程如图1所示,其中各系数参数由相关参考资料[5]中选取。 假设某远火分队需要从A点机动到G点,机动路线如图2所示,共有L个节点,分为L-1条路线,出发点A起始坐标为(x1,y1),到达第二个节点B的坐标为(x2,y2),依次类推,到达最后节点G的坐标为(xn,yn);在A点的出发时刻为T1,到达第二个节点B的时刻为T2,行驶速度为V1,依次类推,到达最后节点G的时刻为Tn,最后一段行驶速度为Vn-1,D、W分别代表各路段地形干扰系数和敌火力干扰系数,U代表气象干扰系数。各路段地形影响因素和敌火力干扰因素不尽相同。 图1 远火机动模型计算流程图Fig.1The calculation flow chart of the long-range rocket maneuvering model 给定初始速度为45km/h,出发时刻开始计时,对每一路段的地形系数和(实际数值的计算应根据实际地形和作战情况而定),根据上述公式,可求出相应节点的时刻和坐标,进而求得行驶路程。将所计算得出的结果利用仿真软件可得出对应速度和时间关系图,时间与路程的关系图,如图3、图4所示。 从上述两图可以发现远火分队机动速度的变化整体成平稳状态,在局部受其他因素影响速度发生变化,但变化幅度不大,而机动路程整体随时间变化基本可看做成线性变化。若将远火分队分为若干子单元,则同一图中进行叠加即可实现。 利用上述机动模型仿真得出的结果可以作为作战指挥员在战场了解远火分队机动的位置和时间的参考依据,对了解远火分队的机动过程有一个直观的认识。以上计算结果所得的图形是相对较为简单的数据生成,其各影响系数值的设定也较为理想化,在实际作战运用中,坐标的建立还需依靠实际作战地图,而各影响系数的计算是多种影响因素共同作用的结果,所得的图形也更为复杂。 图2 某远火分队机动路线图Fig.2 The maneuvering roadmap of certain long-range rocket unit 图3 某远火分队在机动过程中的时间与速度关系图Fig.3The relationship of the time and speed of certain long-range rocket unit in the maneuvering process 图4 某远火分队在机动过程中的时间与路程关系图Fig.4The relationship of the time and route of certain long-range rocket unit in the maneuvering process 远火分队的动态机动模型研究是今后研究远火武器系统战斗损伤的重要组成部分。笔者对机动过程中存在的影响因素进行分析,对机动过程中的速度和位移进行了计算,并给出了研究远火分队机动模型的计算流程图。文章存在的不足之处在于文章默认远火分队各装备之间的速度关系和位置关系是恒定的,忽略了远火分队内部因素对其速度和位移的影响。在以后的研究中将对其内部之间的相互位置关系进行分析。 [1] 党崇民,张羽.联合作战学[M].北京:解放军出版社,2009. DANG Chongmin,ZHANG Yu.Joint operation science[M].Beijing:PLA Publishing Press,2009. [2] 张广苏.远程多管火箭炮武器系统[M].南京:炮兵学院南京分院,2006. ZHANG Guangsu.Long-range rocket system[M].Nanjing:The Artillery Academy NanjingCollege,2006. [3] 蒋英杰,李欣欣,闫志强,等.增长因子动态模型Bayes可靠性评定[J].计算机仿真,2008.25(8):73-75. JIANG Yingjie,LI Xinxin,YAN Zhiqiang,et al.The bayesian reliability evaluation based on dynamic modeling method of growth factor[J].Computer Simulation,2008.25(8):73-75. [4] 张景新,王亮.火炮战损率动态模型的建立与运用研究[J].火炮发射与控制学报,2008.(1);94-96. ZHANG Jingxin,WANG Liang.Dynamic model establishment and operational research of artillery combat damage rate[J].Journal of Gun Launch& Control,2008,(1);94-96. [5] 郭齐胜,曹晓东.作战模拟基础[M].装甲兵工程学院,2006. GUO Qisheng,CAO Xiaodong.Operational simulation basis[M].The Academy of Armored Forces Engineering,2006. The Research on the Dynamic Model in the Maneuvering Process of Long-range Rocket Unit WANG Bin1,HUANG Shaoluo1,WANG Guangyan2 (1.Staff Room of Military,Ordnance Engineering College; 2.Department of Equipment Command and Management,Ordnance Engineering College,Shijiazhuang 050003,China) Nowadays,The battlefield pays more and more attention on the long-range rocket weapon system because of its characteristics of fast launch speed,long range,fierce fire,strong power,good maneuverability and easy to operate.In this paper,the current domestic research status of the maneuvering process of the weaponry was analyzed and the influence factors of the long-range rocket unit in the maneuvering process was analyzed from six aspects combined with the characteristics of the long-range rocket unit.The motor speed,the coordinates and time of reaching the specified location of the long-range rocket unit in the maneuvering process was described and analyzed by the model,and the dynamic maneuvering process was described by mathematical formula.The flow chart of the long-range rocket unit in the maneuvering process was also established.The certain examples was analyzed according to the mathematical model and the relationship chart between certain speed,time and distance was obtained by MATLAB software simulation.The research on the dynamic model in the maneuvering process of long-range unit is a very importance step,which has important significance to the research on the battlefield damage simulation of long-range rocket weapon system. long-range rocket unit; maneuver; dynamic model 王 彬 男(1986-),山西盂县人,硕士研究生,主要研究方向为装备保障理论与应用。 黄少罗 男(1965-),湖南双峰人,教授,主要研究方向为装备保障理论与应用。 E 917 A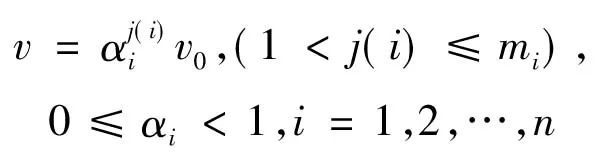




4 结束语