强拟α-预不变凸性与最优化

李 婷

(山西大学商务学院,山西 太原 030031)



强拟α-预不变凸性与最优化

李 婷

(山西大学商务学院,山西 太原 030031)

考虑了一类重要的广义凸函数-强拟α-预不变凸函数,首先给出了强拟α-预不变凸函数的一个性质,然后讨论了强拟α-预不变凸函数分别在带不等式约束的非线性规划问题及多目标规划问题中的应用,得到了一些最优性结果.

强拟α-预不变凸函数;拟α-预不变凸函数;非线性规划;多目标规划

凸性及广义凸性在经济均衡、管理科学、对策论及数学规划等理论中起着非常重要的作用.近年来,对凸性和广义凸性的研究已经成为优化研究中的一个重要课题.然而凸函数相对较少,广义凸函数有许多类似于凸函数的性质,因此对广义凸函数的研究非常有必要,并且取得了一系列重要的成果.1981年,Hanson在文献[1]中提出了不变凸函数;1988年,Weir和Mond, Weir和Jeyakwma先后在文献[2]和[3]中引入了不变凸集和预不变凸函数的定义,研究了预不变凸函数的性质及其在最优化中的应用.2001年,Yang和Li在文献[4]中又引进了严格预不变凸函数和半严格预不变凸函数的概念,得到了它们的一些性质及其在数学规划中的应用.2006年,Tang和Yang在文献[5]中引进了强预不变凸函数的定义,而且进一步分析了这个函数与预不变凸函数、严格预不变凸函数及半严格预不变凸函数之间的关系.同年,Noor M A和Noor K I在文献[6]中提出了两类新的广义凸函数——α-预不变凸函数和拟α-预不变凸函数. 2007年,刘彩平和杨新民在文献[7]中引入了强预拟不变凸函数和强拟不变凸函数的概念,讨论了强预拟不变凸函数的性质,并研究了强预拟不变凸函数在多目标优化中的应用. 2008年,刘彩平在文献[8]中进一步将拟α-预不变凸性推广到强拟α-预不变凸性,在适当的条件下建立了强拟α-预不变凸性,强拟α-不变凸性之间的关系.

在这些文献的基础上,本文对文献[7]的部分结果加以推广,首先给出了强拟α-预不变凸函数的一个性质,然后讨论了强拟α-预不变凸函数分别在带不等式约束的非线性规划问题及多目标规划中的应用,得到了一些最优性结果.这些结果在一定程度上完善了对强拟α-预不变凸函数的研究.

1 预备知识

设H是定义了内积〈·,·〉和范数‖·‖的实Hilbert空间,K是H的一个非空子集,

定义1.1[6]如果∀x,y∈K,∀λ∈[0,1],有

则称集合K为α-不变凸集．

定义1.2[6]设集合K是关于α和η的α-不变凸集,若∀x,y∈K,∀λ∈[0,1],有

则称f是K上关于α和η的α-预不变凸函数;

定义1.3[6]设集合K是关于α和η的α-不变凸集,若∀x,y∈K,∀λ∈[0,1],有

则称f是K上关于α和η的拟α-预不变凸函数.

定义1.4[8]设集合K是关于α和η的α-不变凸集,若∀x,y∈K,∀λ∈[0,1],∃β>0,有

则称f是K上关于α和η的强拟α-预不变凸函数．

根据定义1.3和定义1.4,易知强拟α-预不变凸函数一定是拟α-预不变凸函数.

2 强拟α-预不变凸函数的性质

定理2.1 设K⊆Rn是关于α和η的α-不变凸集,令I为有限或无限指标集,函数fi:K→R(i∈I)是K上关于α和η的强拟α-预不变凸函数,记f(x)=sup{fi(x),i∈I},∀x∈K.如果∀x∈K,∃ij=i(x)∈I,使得f(x)=fj(x),那么f(x)一定是K上关于α和η的强拟α-预不变凸函数.

证明 假设f(x)不是K上关于α和η的强拟α-预不变凸函数.则∀β>0,∃x,y∈K,∃λ∈(0,1),使得

(1)

令z=y+λα(x,y)η(x,y),由已知条件,存在i(z)=i0,i(x)=i1,i(y)=i2,满足

因为fi:K→R(i∈I)是K上关于α和η的强拟α-预不变凸函数,则∃β0>0,有

(2)

(3)

于是由(2)和(3)得

即f(z)=f(y+λα(x,y)η(x,y))≤max{f(x),f(y)}-β0λ(1-λ)‖η(x,y)‖2

上式与式(1)矛盾,假设不成立,即f(x)=sup{fi(x),i∈I}一定是K上关于α和η的强拟α-预不变凸函数.

3 强拟α-预不变凸函数在带不等式约束的规划问题中的应用

考虑下面的约束非线性规划问题:

(P)minf(x)

其中K是Rn的非空子集,f,gi:K→R,i=1,…,m

可行解集D={x∈K|gi(x)≤0,i∈J}.

(4)

(5)

由于gi:K→R(i∈J)在K上是拟α-预不变凸函数,则∀i∈J,λ∈[0,1],有

(6)

综合(5)和(6)式可知

(7)

4 强拟α-预不变凸函数在多目标规划中的应用

考虑下面的多目标规划问题

其中F:K→RP,fi:K→R(i=1,…,p),K⊆Rn是关于α和η的α-不变凸集.

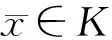
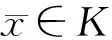
定理4.1设集合K⊆Rn是关于α和η的α-不变凸集,x≠y时,有η(x,y)≠0,

α(x,y)≠0.fi(x)(i=1,…,p)是K上关于α和η的拟α-预不变凸函数.若∃j0(1≤j0≤p),fj0(x)在K上关于相同的α和η是强拟α-预不变凸函数,则(VP)的局部有效解也是全局有效解.

(8)

(9)

(10)

定理4.2 设集合K⊆Rn是关于α和η的α-不变凸集,x≠y时,有η(x,y)≠0,

α(x,y)≠0.f1(x),f2(x),…,fp(x)是K上关于α和η的强拟α-预不变凸函数,则(VP)的局部弱有效解也是全局弱有效解.

(11)

(12)

[1] Hanson.M.A.On sufficiency of the Kuhn-Tucker conditions[J].Journal of Mathematical Ana-lysis and Applications,1981,80:545-550

[2] WEIR T,MONG B.Preinvex functions in multiple objective optimization[J].Journal of Math Anal and Appl,1988,136:29-38

[3] WEIR T,JEYAKUMAR V.A class of nonconvex functions and Mathematical programming[J].Bull Austral Math Soc,1988,38:177-189

[4] YANG X M, LI D.Semistrictly preinvex functions[J].Journal of Mathematical Analysis and Ap-plications,2001,258:287-308

[5] TANG W M,YANG X M.The sufficiency and necessity conditions of strongly preinvex functio-ns[J]. 运筹学学报,2006(3):50-58

[6] NOOR M A,NOOR K I.Some characterizations of strongly preinvex functions[J].Journal of Mat-hematical Anaiysis and Applications,2006,316,697-706

[7] 刘彩平,杨新民.强预拟不变凸函数和强拟不变凸函数[J].经济数学,2007,24(4):414-419

[8] 刘彩平.几类广义不变凸函数及其性质[D].重庆:重庆师范大学,2008

[9] 林锉云,董加礼.多目标优化的方法与理论[M].长春:吉林教育出版社,1992

The Strongly Quasi α-Preinvexity and Optimization

LI Ting

(Fundamental Teaching Department,the Business College of Shanxi University,Taiyuan 030031, China)

A class of generalized convex functions, termed strongly quasi α-preinvex functions, is considered. Firstly, one property of strongly quasi α-preinex functions is given. Then, some optimality results are obtained in nonlinear programming problems with inequality constraint and multibjective optimization problems.

strongly quasiα-preinex functiongs; quasi α-preinex functions; nonlinear programming; multibjective optimization

2016-06-08

李 婷(1981-),女,山西永济人,硕士,山西大学商务学院讲师,从事最优化理论与应用研究．

1672-2027(2016)03-0016-04

O221

A