基于灰色马尔可夫链组合模型的兰州铁路局集装箱运量预测
邱 菲
(兰州铁路局 客货运输统计所,甘肃 兰州 730000)
基于灰色马尔可夫链组合模型的兰州铁路局集装箱运量预测
邱 菲
(兰州铁路局 客货运输统计所,甘肃 兰州 730000)
阐述灰色马尔可夫链组合模型理论,在分析兰州铁路局集装箱运输现状及特点的基础上,以兰州铁路局集装箱运量现状及历史数据为依据,运用灰色马尔可夫链组合模型对兰州铁路局集装箱运量进行预测分析,为铁路部门制定物流营销政策、科学组织货物运输提供参考。
铁路;集装箱;运量预测;灰色预测;马尔可夫模型
集装箱运输作为我国铁路运输重点发展方向,具有标准统一、方便运输、环境友好等优势,目前全路正在大力建设集装箱中心站,积极将集装箱运输作为铁路运输发展的主要方向之一。选用基于灰色马尔可夫链组合模型进行铁路集装箱运量预测,为科学分析和预测集装箱运量提供理论支持。
1 灰色马尔可夫链组合模型
1.1 灰色马尔可夫链组合模型概述
随着自然科学的发展和计算机应用技术的不断推广,多种交通量预测模型产生,预测的准确性也随之提高[1]。常用的预测方法可以分为定性预测和定量预测。定性预测方法主要以专家为索取信息的对象,组织相关专家,通过对过去和现在发生的问题进行综合分析,从中找出规律,对未来作出判断[2]。定性预测方法包括集体意见法、头脑风暴法、德尔菲法、情景分析法等。定量预测方法是用定量分析研究运量的发展趋势,它以历史统计资料和有关信息为依据,运用各种数学方法预测未来货运市场需求情况[3]。定量预测方法包括时间序列预测法、因果分析预测法、灰色预测法、组合预测法等。
铁路集装箱运量预测受多种因素影响,主要包括社会经济因素、箱源基础、设施条件和服务水平、政策及其他因素。在铁路集装箱运量的影响因素中,有的因素可以量化,有的因素只能做定性分析。随着经济社会的快速发展,以及铁路推进现代物流转型发展、实施铁路供给侧改革、转变服务观念,在这种背景下,影响铁路货物运量的因素更加复杂,而这些因素部分是确定的,部分是不确定的。灰色系统预测避开系统复杂的相互关系,着眼于系统本身的灰色信
息,通过处理原始数据和建立灰色模型,掌握系统发展规律,对系统的未来状态做出科学的定量预测,达到使灰色系统白化的目的[4]。GM (1,1) 模型是灰色系统预测理论的基本模型和具体应用。GM 代表灰色模型(Grey Model)[5],第 1 个数字“l”表示微分方程的阶数,第 2 个数字“1”表示只含 1 个变量。灰色系统预测理论的基本思路是将已知的数据序列按照某种规则构成动态或非动态的白色模块,再按照某种变换或解法来求解未来的灰色模型,在灰色模块中再按照某种准则,逐步提高白度,从而确定系统在未来发展变化的趋势,为事物的规划决策、系统的控制与状态的评估提供依据[6]。灰色系统预测具有预测精准度高、无需大量有规律样本、计算工作量小等优点[7],但其预测结果精确度受原始数据变化幅度的影响较大,可以通过结合马尔可夫链修正的灰色预测来体现GM (1,1) 预测数据时间序列宏观上的变化规律,以及马尔可夫链预测数据时间序列的微观波动规律,使预测结果得到较大改善,其精度明显优于传统的灰色马尔可夫模型或单一的灰色预测模型[8]。因此,选用基于灰色马尔可夫链组合模型对集装箱运量进行预测,并且进行算例验证。
1.2 构建灰色马尔可夫链组合模型
(1)原始数列生成累加数列[9]。记原始数列为x(0)= (x(0)(1),x(0)(2),…,x(0)(k),…,x(0)(n)),x(0)表示 x(0)(k) 中第 k 个原始数据,n 表示原始数据的个数。对原始数列经过一次累加后生成累加数列为x(1)= (x(1)(1),x(1)(2),…,x(1)(k),…,x(1)(n)),其中,。
(2)构造均值数列。对 x(1)作紧临均值生成均值数列 z(1)= (z(1)(1),z(1)(2),z(1)(3),…,z(1)(k),…,z(1)(n)),其中,z(1)(k) = 0.5x(1)(k) + 0.5x(1)(k-1),k = 2,3,…,n。
(3)求解灰色参数。将紧临均值数据代入灰色微分方程 x(0)(k) + ax(1)(k) = b 中,k = 2,3,…,n,a,b为灰色参数,记


用最小二乘法求解灰色参数,得

(4)建立灰色模型预测公式。

(5)残差检验。模型相对残差可以表示为

如果 |δ (k+ 1)| < 16%,则模型达到一般要求;如果 |δ (k+ 1)| < 8%,则模型达到较高要求。
(6)对预测结果进行马尔可夫链修正。
①预测效果状态划分。根据马尔可夫链随机过程分析方法的应用经验及相对残差幅度分布情况,对预测效果进行状态划分,如表 1 所示。
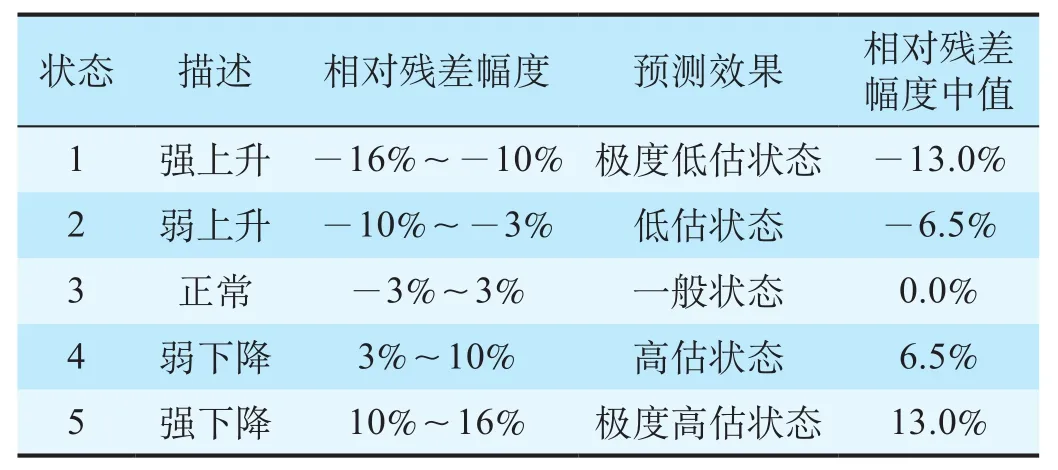
表 1 预测效果状态划分标准
②生成预测结果转移概率矩阵。记 aij表示状态 i转移到状态 j 的次数之和,ai表示状态 i 转移到其他状态的次数之和,从状态划分情况可得出状态转移情况,如表 2 所示。
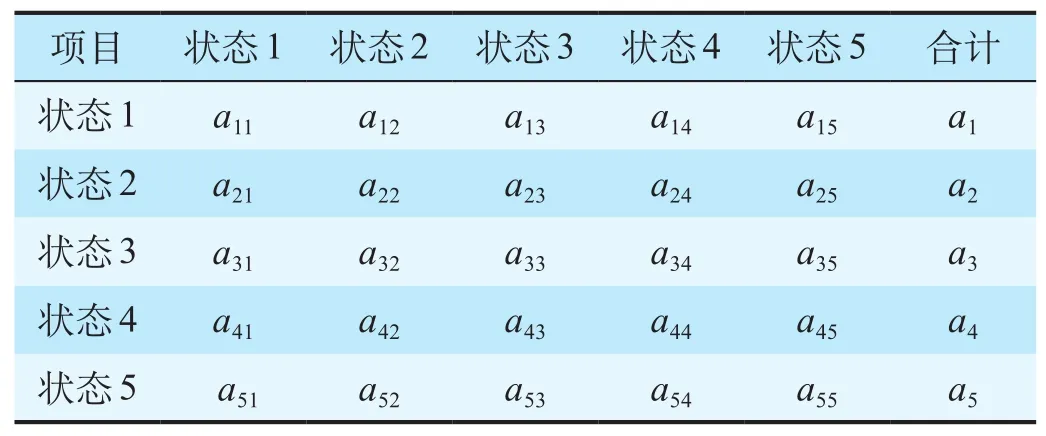
表 2 预测结果转移
根据表 2,可得预测结果转移概率矩阵为

式中:P 为 aij占 ai的比率,即状态 i 转移到状态 j 的次数之和占状态 i 转移到其他状态的次数之和的比率。pij的计算公式为

③生成预测状态向量。根据马尔可夫链预测模型,得到预测状态向量

式中:k=0,1,…,n,A(0)为初始时刻的状态概率向量,,为初始时刻的状态 i 对应的取值,当初始时刻的状态为状态i 时,,否则为 k + 1时刻的预测状态概率向量,为 k + 1 时刻的状态 i 对应的取值。
④生成修正后的预测值。对公式 ⑵ 得出的预测值进行修正,修正表达式为

式中:Qi表示状态i 的相对残差幅度中间值。
2 兰州铁路局集装箱运量预测分析
2.1 兰州铁路局集装箱运输现状及特点
兰州铁路局位于全国铁路网西北部,跨越甘肃省和宁夏回族自治区,处于亚欧大陆桥在中国境内的重要区段,东连西安,西通乌鲁木齐,南接西宁,北望银川,是西北交通运输和经济建设的大动脉。兰州铁路局货源结构以资源输出为主,产成品输出为辅。自2005 年起,兰州铁路局货物发送量稳步攀升,2012年达到历史高点,2013 年同比开始下降,但铁路集装箱运量除2013 年有所回落外,整体呈线性上涨的趋势,自2005 年的 113 万 t 至 2015 年的 445 万 t,累计上涨 332 万 t。2015 年以来,兰州铁路局实施了现代物流转型发展战略,货物运输水平和服务水平得到显著提升,其中集装箱运输对全局铁路货运量增长贡献突出。兰州铁路综合货场项目是全路 18 个区域性集装箱中心站之一,该项目预计 2017 年初建成,投入运营后,将成为西北地区集装箱装卸、运输的中心和枢纽,通过铁路实现与全国其他中心站的联通,兰州铁路局集装箱运量将呈现快速增长态势。兰州铁路局2005—2015 年集装箱发送量趋势如图 1 所示。

图 1 兰州铁路局 2005—2015 年集装箱发送量趋势图
兰州铁路局集装箱运输有以下特点:一是集装箱发送量增幅明显,占比逐年增加。由 2006 年的 2.3%增加到 2015 年的 5.9%,10 年时间集装箱占比翻了近2 番,可见集装箱运输越来越得到市场的认可,也是未来兰州铁路局货运增长的一个亮点。二是主要集装箱办理站发送量增幅明显,发货人较为集中。三是集装箱装运的品名众多,主要品类占比较大,如 2015 年集装箱钢铁运量占集装箱发送量的近 80%。四是集装箱运输多为长距离运输,运距集中在 1 000~3 500 km。五是铁路集装箱运费较低。
2.2 基于灰色马尔可夫链组合模型的集装箱运量预测
(1)以兰州铁路局 2005—2015 年集装箱运量为参考数据,生成原始数列 x(0),并且对原始数列进行一次累加生成累加数列 x(1),如表 3 所示。

表 3 2005—2015 年兰州铁路局铁路集装箱发送量原始数列及累加数列
(2)对 x(1)作紧临均值生成新的数列 z(1),具体数值如表 4 所示。

表 4 x(1)的紧临均值生成数列z(1)
(3)将表 4 中 z(1)(k) 数据代入公式⑴,得

(4)根据公式 ⑵,兰州铁路局集装箱货物发送量灰色预测模型可表示为

(5)检验残差。根据集装箱发送量的灰色模型计算 2006—2015 年集装箱运量预测值,预测结果如表 5 所示。

表 5 兰州铁路局集装箱发送量的 GM (1,1) 预测结果
由表 5 中预测数据,可得兰州铁路局集装箱发送量预测结果平均残差为 7.7%,在可允许和接受的范围内,可以用来预测,但准确度仍然有待进一步提高。
(6)对预测结果进行马尔可夫链修正。根据马尔可夫链随机过程分析方法的应用经验及相对残差幅度分布情况,对其进行状态划分。根据表 5 中相对残差幅度值及表 1 的预测效果状态划分标准可得,状态2 的弱上升年份为 2010—2012 年、2015 年,状态 3 的正常年份为 2007 年,状态 4 的弱下降年份为 2006年、2008 年、2009 年、2014 年,状态 5 的强下降年份为 2013 年。兰州铁路局 2006—2015 年集装箱运量预测结果状态转移情况如表 6 所示。
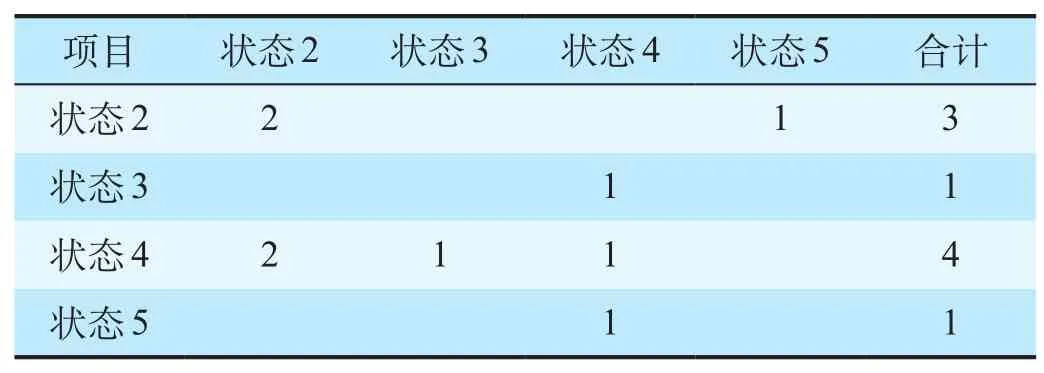
表 6 集装箱运量预测结果转移

根据表 6 可得兰州铁路局集装箱运量转移概率矩阵 P。 2015 年相对残差为 -4.56%,其预测结果状态划分至状态 2,其状态概率向量可表示为:A(0)= (1,
0,0,0)。根据公式 ⑹,得到兰州铁路局 2016—
2020 年集装箱运量预测状态向量,如表 7 所示。

表 7 兰州铁路局 2016—2020 年集装箱运量预测状态向量
根据公式 ⑺,经马尔可夫链修正后得到的 2016—2020 年的预测结果如表 8 所示。
通过马尔可夫链对集装箱运量预测值进行修正后,平均相对残差为 3.05%,较之前灰色 GM(1,
1) 预测模型的平均相对残差 7.7% 相比,精度明显提高,预测准确度得到较大改善,体现了灰色马尔可夫链组合模型的优点。在使用灰色 GM(1,1) 进行集装箱运量预测的过程中,发现突变性因素无法在灰色预测模型中反映,如铁路集装箱运量在 2010—2012 年上升过快,而在 2013 年有所下降等。能够明显看到2008 年、2011 年、2012年、2013 年和 2014 年的拟合数据与实际数据存在较大的差距,相对残差分别为9.99%、-9.55%、-9.44%、11.83% 和 9.7%,远远高于平均相对残差 7.7%。一般的模型无法处理突变因素,甚至受突异点的影响,将误差带到预测中,而马尔可夫状态转移将历史的波动信息考虑进来,使得预测结果准确度提高[10]。

表 8 基于灰色马尔可夫链组合模型的兰州铁路局集装箱运量预测结果
3 结束语
集装化运输由于中途运输换装次数少、机械化程度和装卸效率高、运费比较优惠,能够提升运输货品的安全性,降低货品的损毁率,在市场竞争中具有优势。大力发展集装箱运输,突出集装箱运输优势,扩大铁路集装箱运输占比,是实现铁路向现代物流转型的手段之一。利用灰色马尔可夫链组合模型进行预测,能够发挥灰色系统预测模型的优点,并在考虑原始数据影响的基础上,考虑历年状态转移情况,避免了灰色系统预测模型受原始数据变化幅度影响大的缺点。基于灰色马尔可夫链组合模型的集装箱运量预测,为铁路科学确定考核指标、合理安排车辆运用计划提供重要的依据,其分析结果对于铁路部门制定物流营销政策、科学组织货物运输具有重要作用。
[1] 宋光平. 铁路货运量预测方法研究[D]. 北京:北京交通大学,2007.
[2] 罗安全. 铁路现代物流中心的构建与运作模式研究[D].长沙:中南大学,2009.
[3] 程礼芬. 区域货运量预测方法的比较[J]. 重庆交通学院学报,2005,24(4):114-116. CHENG Li-fen. Compare of Regional Freight Volume Forecast Methods[J]. Journal of Chongqing Jiaotong University,2005,24(4):114-116.
[4] 郭 晶,姜秀山. 铁路集装箱运量发展预测[J]. 物流科技,2006,29(1):31-34. GUO Jing,JIANG Xiu-shan. Application of Grey System to the Forecast of the Railroad Container Volume[J]. Logistics Technology,2006,29(1):31-34.
[5] 吴 璇,王 烈. 组合预测模型在铁路集装箱运量预测中的应用[J]. 铁道运输与经济,2010,32(10):90-94. WU Xuan,WANG Lie. Application of Combined Forecasting Model in Railway Container Prediction[J]. Railway Transport and Economy,2010,32(10):90-94.
[6] 张 诚,周湘峰. 基于灰色预测-马尔可夫链-定性分析的铁路货运量预测[J]. 铁道学报,2007,29(5):15-21. ZHANG Cheng,ZHOU Xiang-feng. Railway Freight Volume Forecasting based on Grey Prediction-Markov-Qualitative Analysis[J]. Railway Transaction,2007,29(5):15-21.
[7] 张 玥,帅 斌. 基于改进灰色模型的东北地区铁路货运量预测[J]. 铁道科学与工程学报,2012,9(5):125-128. ZHANG Yue,SHUAI Bin. Railway Freight Volume Forecast in Northeast Region based on the Improved Gray
Model[J]. Journal of Railway Science and Engineering,2012,9(5):125-128.
[8] 谢建文,张元标,王志伟. 基于无偏灰色模糊马尔可夫链法的铁路货运量预测研究[J]. 铁道学报,2009,31(1):1-7. XIE Jian-wen,ZHANG Yuan-biao,WANG Zhi-wei. Railway Freight Volume Forecasting based on Unbiased Grey -Fuzzy-Markov Chain Method[J]. Journal of the China Railway Society,2009,31(1):1-7.
[9] 于 洋,杨学斌,杜 文. 基于灰色-马尔可夫链改进方法的预测方法[J]. 统计与决策,2013(13):53-55.
[10] 李金龙,张红亮. 我国铁路集装箱运输发展对策的思考[J]. 铁道货运,2013,31(1):47-50. LI Jin-long,ZHANG Hong-liang. Thoughts on the Development of Railway Container Transportation in China[J]. Railway Freight Transport,2013,31(1):47-50.
(责任编辑 王 静)
Container Transportation Volume Prediction of Lanzhou Railway Administration based on Gray Markov Combination Chain Model
QIU Fei
(Passenger and Freight Transportation Statistical Institute, Lanzhou Railway Administration, Lanzhou 730000, Gansu, China)
Through elaborating on the Gray Markov combination chain model theory, this paper analyses Present situation and characteristics of container transportation of Lanzhou Railway Administration, and applies Markov combination chain model for prediction and analysis for container transportation volume of Lanzhou Railway Administration based on current status and historical data, which provides
for railway department to formulate logistic marketing policy and scientifically organize freight transportation.
Railway; Container; Freight Volume Prediction; Gray Prediction, Markov Model
1004-2024(2016)09-0024-06
U294.3
B
10.16669/j.cnki.issn.1004-2024.2016.09.06
2016-07-25
邱菲(1982—),女,天津人,大学本科。

