混凝土材料球形空腔膨胀的数值研究

晋小超,杨华伟,王志华,树学峰

(太原理工大学 应用力学与生物医学工程研究所,太原 030024)



混凝土材料球形空腔膨胀的数值研究

晋小超,杨华伟,王志华,树学峰

(太原理工大学 应用力学与生物医学工程研究所,太原 030024)

为研究混凝土材料动态球形空腔膨胀的机理,采用LS-DYNA对其进行了数值模拟。结果表明，空腔界面压力与膨胀速度平方成正比,密度与膨胀速度平方成反比,且膨胀速度随抗压强度的提高而降低;而空腔初始半径,及混凝土材料的抗拉强度等对空腔界面的膨胀速度基本没有影响。对膨胀过程中模型径向应力的分布情况进行了分析,并与空腔膨胀理论进行了对比,二者保持一致。通过对不同强度混凝土动态球形空腔膨胀的数值分析,拟合了空腔界面膨胀速度到达稳定时对应的临界速度的计算公式,建立了空腔压力与界面膨胀速度的函数关系,并依此给出了混凝土靶体侵彻深度的计算公式。通过与实验数据对比,验证了公式的正确性和适用性,表明空腔膨胀数值模拟结果可以用于侵彻深度计算。

混凝土;球形空腔膨胀;临界压力;侵彻深度;数值研究

空腔膨胀理论在岩土材料的侵彻与穿甲研究中得到了广泛的应用,但理论本身并不完善。BISHOP和HILL et al[1-2]最早提出了球形和柱形空腔膨胀理论,通过理论推导研究了空腔在土壤介质中的膨胀问题。GOODIER[3]将空腔膨胀理论用于不可压缩弹塑性固体,提出了动态球形空腔膨胀理论,研究了球形弹体侵彻金属靶体问题,讨论了球形弹侵入半无限大土壤靶体问题。FORRESTAL,LUK et al[4-6]将空腔膨胀理论应用到可压缩的靶体模型中,建立了弹体在靶体中的阻力模型,并且与实验结果吻合较好。FORRESTAL et al[7]将球形和柱形空腔膨胀理论应用到混凝土靶体中,推导空腔表面的应力与膨胀速度的表达式,由此得到了弹体侵彻半无限大混凝土靶体的半经验公式,比较了可压缩模型与不可压缩模型、弹性-塑性模型与弹性-裂纹-塑性模型与混凝土侵彻实验数据的吻合情况。

近年来,国内学者也对不同材料的空腔膨胀理论做了大量研究。王延斌等[8]利用静态空腔膨胀理论求出了脆性材料时的空腔膨胀压力,并据此求出了弹体撞击脆性材料时的侵彻深度计算公式。黄民荣等[9]采用GRIFFITH强度理论,发展了弹丸深侵彻混凝土靶的动态空腔膨胀模型,建立了深侵彻理论计算公式。王一楠等[10]用有限元方法对混凝土材料动态球形空腔膨胀进行了数值模拟。

混凝土作为建筑材料被广泛应用于民事和军事工程中,因此混凝土在冲击载荷作用下的响应一直是防护工程的研究热点。但是由于混凝土是一种脆性材料,本构模型复杂,而且各种空腔膨胀模型中的参数难以准确测量,限制了空腔膨胀理论的进一步发展,因而混凝土靶体在侵彻和穿甲过程中的响应机制也一直未能被准确描述。因此,对混凝土材料动态球形空腔膨胀理论的数值研究成为了一种新的研究方向,而且现有计算软件也可保证数值研究的精确度。本文通过采用LS-DYNA软件的系列模拟,对混凝土动态空腔膨胀过程的影响因素进行了分析,拟合得到了不同强度混凝土靶体中空腔膨胀速度达到稳定值对应的临界压力计算公式,并建立了空腔表面膨胀压力与空腔边界膨胀速度间函数关系,进而得到了弹体侵彻混凝土靶体深度的计算公式。

1 动态球形空腔膨胀模型

对于混凝土材料,FORRESTAL[6]分别对可压缩模型和不可压缩模型进行了理论分析,并与实验数据进行了比较,结果表明将混凝土材料视为可压缩材料与实验结果更为吻合。基于HJC模型的状态方程,李志康和黄风雷[11-12]对混凝土材料动态球形空腔膨胀理论做了大量的理论推导,提出了弹性区-开裂区-压实区的动态响应模型,如图1所示。假定混凝土材料空腔初始半径为0,空腔边界膨胀速度为v,r为Euler球坐标系中的空腔半径。当压力足够大使球形空腔膨胀发生时,空腔周围的混凝土内的空隙将被逐渐压实,产生压实区。产生的弹性球面压缩波将以弹性体积波速向周围传播,压缩波达到的区域会形成弹性区。压缩波在传播的同时产生环向拉应力,由于混凝土的抗拉强度远远低于其抗压强度,故在压实区周围产生裂纹,形成开裂区。按照FORRESTAL的理论,当空腔膨胀速度足够大时,开裂区会逐渐被压实区吞噬,最终形成弹性区-压实区的响应模型。

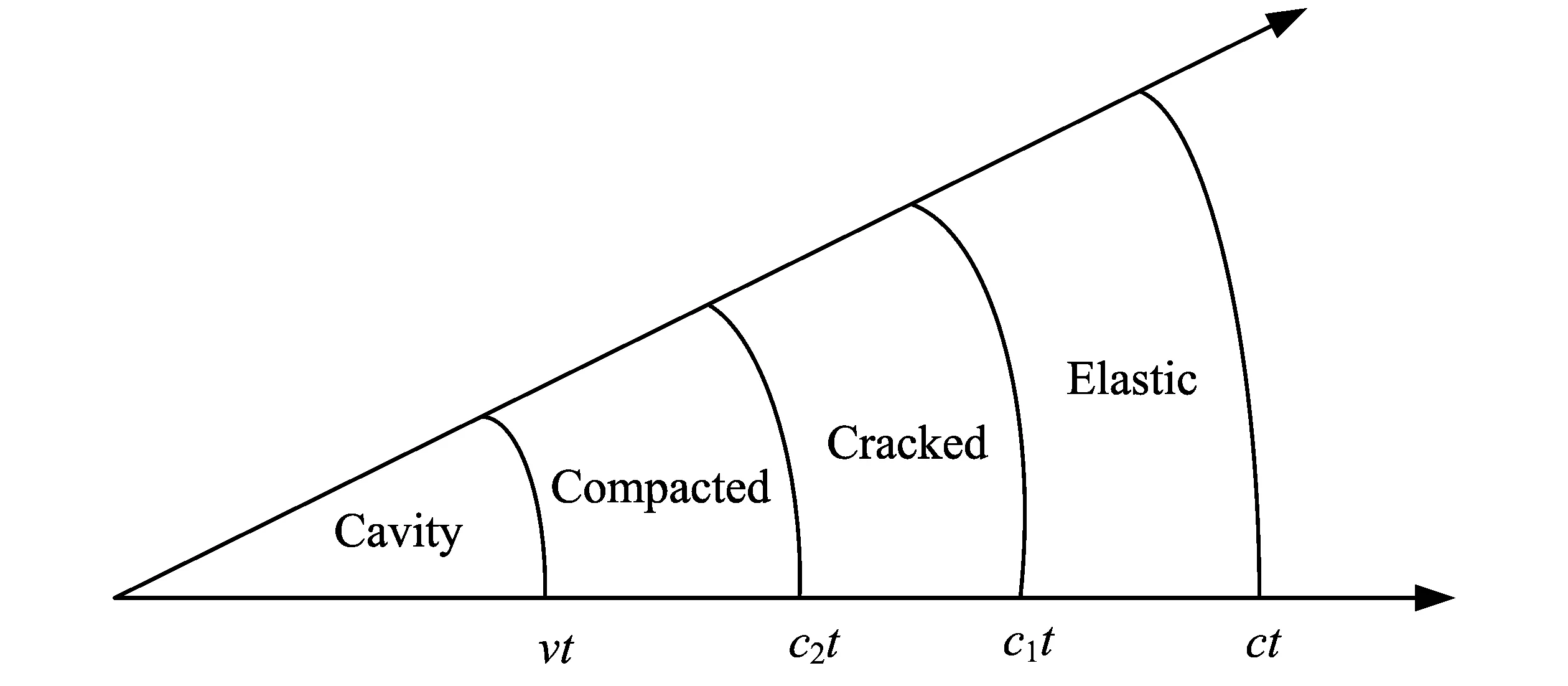
图1 动态球形空腔膨胀响应区域Fig.1 Response region of spherical cavity expansion

2 计算模型和材料模型

2.1 仿真模型

本文采用LS-DYNA软件,建立半径为0.1 m的1/8三维球体模型。通过计算,该半径可保证在计算时间内靶体中膨胀压缩弹性波不会达到靶体的边界,因此可将其视为无限大模型。同时在球体中心预置半径为0.001 m的1/8球形空腔,通过在空腔表面施加沿空腔表面外法线方向的应力p来实现混凝土球体的球形动态空腔膨胀。对球体的对称面节点施加对称约束,对球体的外边界约束全部自由度。采用Solid164 六面体单元对球体进行网格划分,并对球体中心变形较大区域采用局部网格细化,该模型包含实体单元98 700个。通过网格敏感性分析,表明继续细化网格对计算结果没有明显影响。

2.2 材料参数

表1 混凝土的材料模型参数

3 数值模拟结果分析

3.1 空腔边界膨胀速度的影响因素

3.1.1 膨胀压力的影响

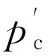
图2 不同压力条件下混凝土空腔边界膨胀速度-时间曲线Fig.2 The cavity wall velocity-time curves of concrete with different pressure

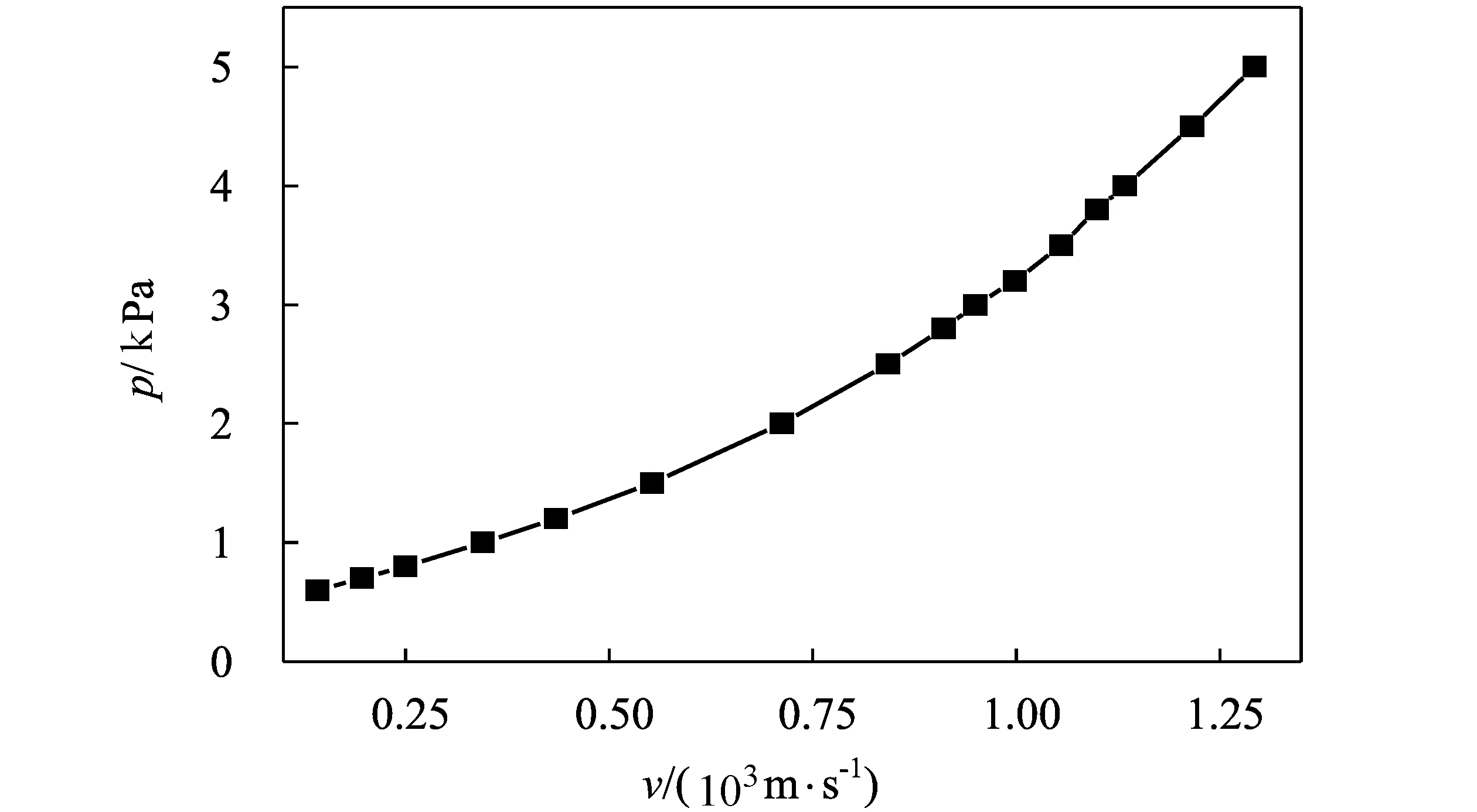
图3 50 MPa混凝土膨胀压力与空腔界面膨胀速度关系曲线Fig.3 The relation of the cavity pressure and expansion velocity for 50 MPa concrete

3.1.2 空腔初始半径的影响

模拟分别采用空腔初始半径r=1,3,5 mm的1/8混凝土球体,膨胀压力为1 500 MPa,分析了空腔初始半径对空腔稳定膨胀速度的影响。如图4所示为空腔半径对膨胀速度影响的模拟结果。结果表明对应较小的空腔初始半径,空腔界面膨胀速度能以更快的速度达到稳定值,但是稳定膨胀速度值与空腔初始半径大小无关。

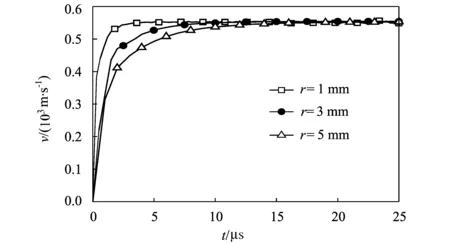
图4 不同空腔初始半径条件下混凝土空腔边界膨胀速度-时间曲线Fig.4 The cavity wall velocity-time curves of concrete with different initial radius of the cavity

3.1.3 材料强度的影响

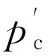
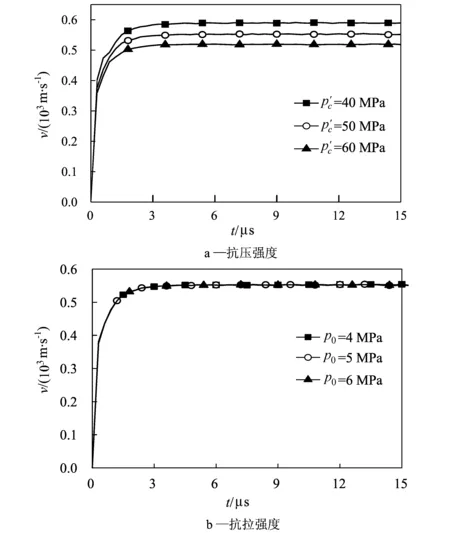
图5 不同强度条件下混凝土空腔界面膨胀速度-时间曲线Fig.5 The cavity wall velocity-time curves of concrete with different initial radius of the cavity

3.1.4 材料密度的影响

为讨论混凝土密度ρ0对空腔膨胀的影响,给定膨胀压力为1 500 MPa,分别采用2 300,2 400,2 500 kg/m3等3种不同密度的50 MPa混凝土材料进行模拟,其他材料参数不变。图6所示为不同密度条件下空腔界面膨胀速度-时间的数值模拟结果。结果表明当膨胀压力一定时,随着混凝土材料密度的增加,空腔界面膨胀的速度将会降低。按照FORRESTAL[7]的理论推导,材料密度与空腔膨胀速度呈反比,为验证其正确性,图7给出了材料密度与膨胀速度二次方的关系曲线。由图知,在膨胀压力一定时,材料密度与膨胀速度二次方近似为反比关系,与理论一致。

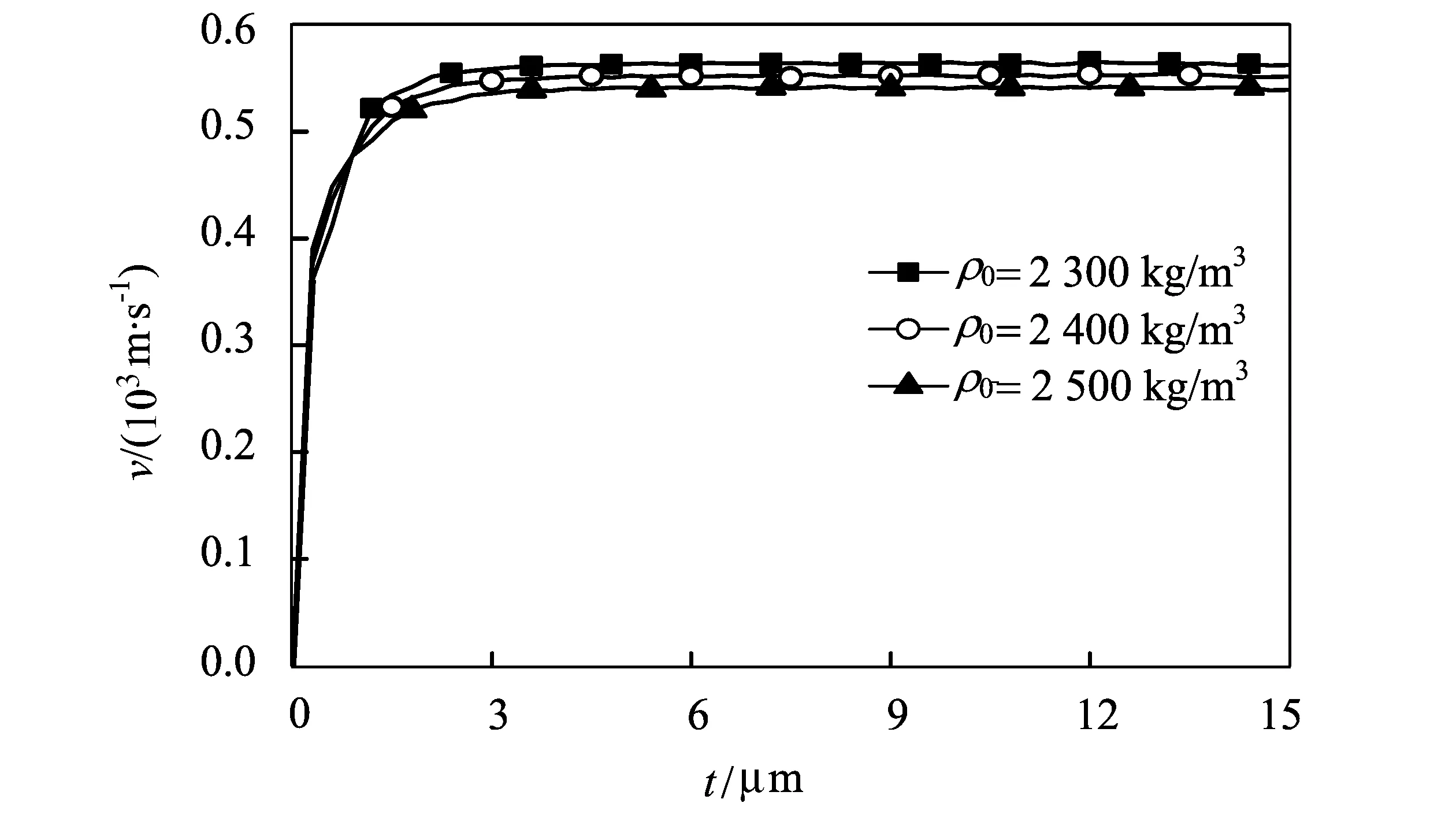
图6 不同密度条件下混凝土空腔界面膨胀速度-时间曲线;Fig.6 The cavity wall velocity-time curves of concrete with different density

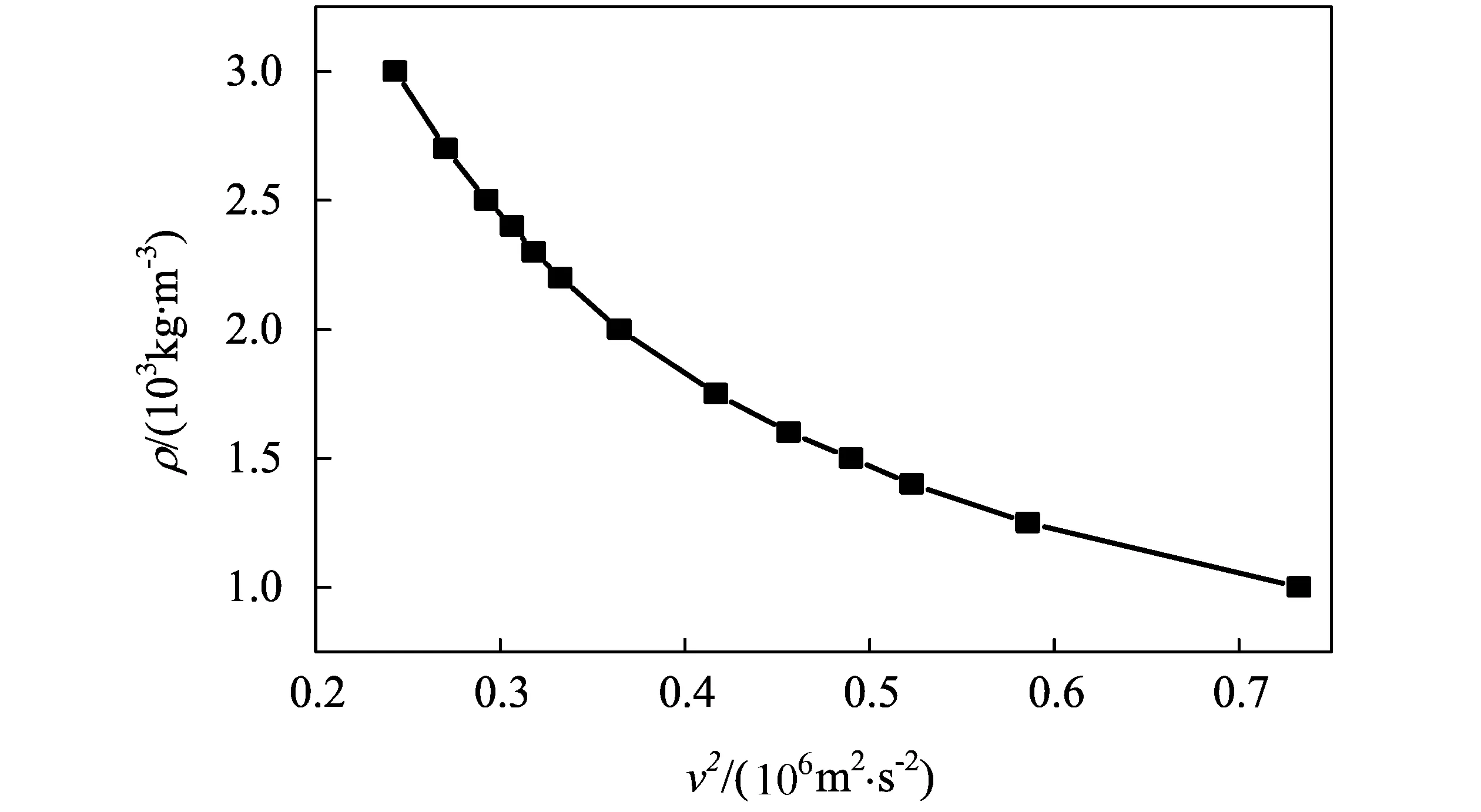
图7 密度与空腔界面膨胀速度二次方关系曲线Fig.7 The relation of the material density and the square of the expansion velocity for 50 MPa concrete

3.2 空腔膨胀模型径向应力分布

由图4可知,对半径为1 mm的50 MPa混凝土空腔边界加载1 500 MPa的载荷,在膨胀开始后3 μs后空腔边界膨胀速度达到稳定值。为讨论混凝土空腔膨胀模型中压力沿径向的分布情况,在t=5 μs时在模型中沿径向取点,输出单元沿径向的应力值,并绘成曲线图与李志康等[11-12]的理论曲线进行对比。如图8所示为t=5 μs时刻径向应力随径向坐标分布的曲线图。在t=5 μs时,空腔边界膨胀了2.3 mm,此时的空腔半径为3.3 mm。数值模拟得到的应力分布情况与理论值吻合的很好。前文已经证明随着膨胀压力的增大,空腔边界的膨胀速度值会增大,而弹性压缩波的速度保持不变,即弹性区与开裂区的边界膨胀速度保持不变,因此随着空腔边界膨胀速度的增大,开裂区必然会被逐渐压缩,进一步证明了FORRESTAL[7]的结论。

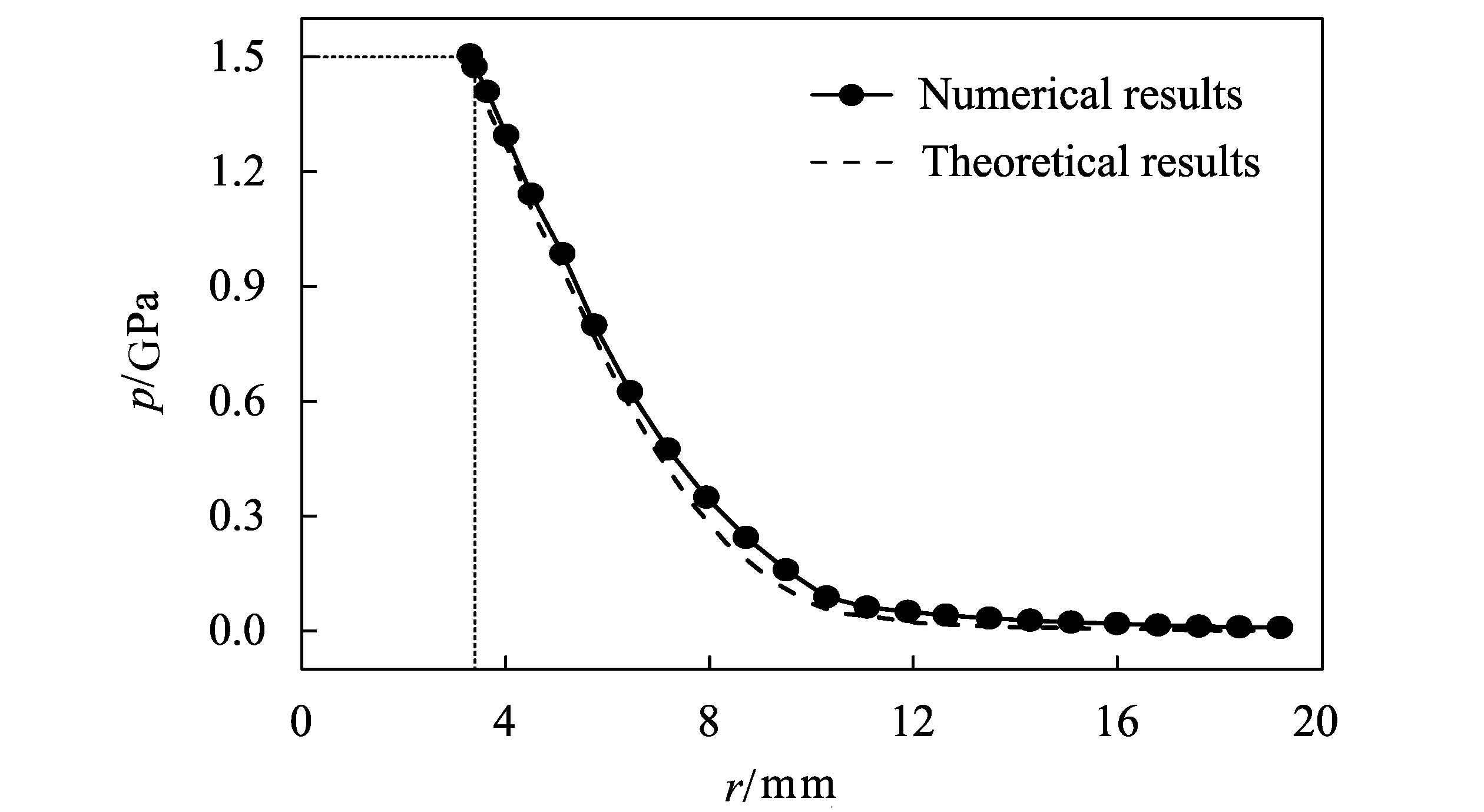
图8 t=5 μs时刻径向应力的数值结果与理论结果对比Fig.8 Numerical and theoretical results of radial stress in concrete at t=5 μs

3.3 空腔边界膨胀速度的公式拟合

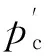
(1)

采用上式拟合,得到无量纲拟合系数值A,D值分别为73.15,-0.50。图10为模拟结果与拟合公式和FORRESTAL经验曲线的对比,可以看到三者吻合较好。按照FORRESTAL[6-7]提出的计算方法,通过引入混凝土材料的抗压强度和密度即可建立空腔表面压力与空腔界面膨胀速度的函数关系,本文采用计算公式如下。

(2)

通过数值拟合,得到无量纲拟合系数B的值为1.12。将抗压强度为30,50,60 MPa的混凝土数值计算得到的结果与拟合得到的公式进行对比,如图11所示,二者相当一致,因此可以认为拟合的公式是可靠的。

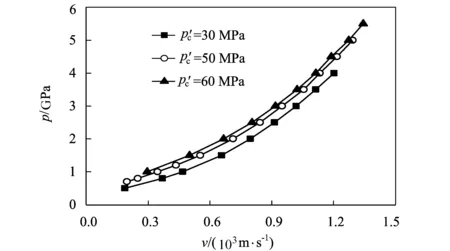
图9 空腔膨胀压力与空腔界面膨胀速度关系曲线Fig.9 The cavity pressure-expansion velocity curves of the cavity wall

图10 空腔膨胀临界压力数值计算结果与拟合公式Fig.10 The numerical results and fitting formula of critical expansion pressure

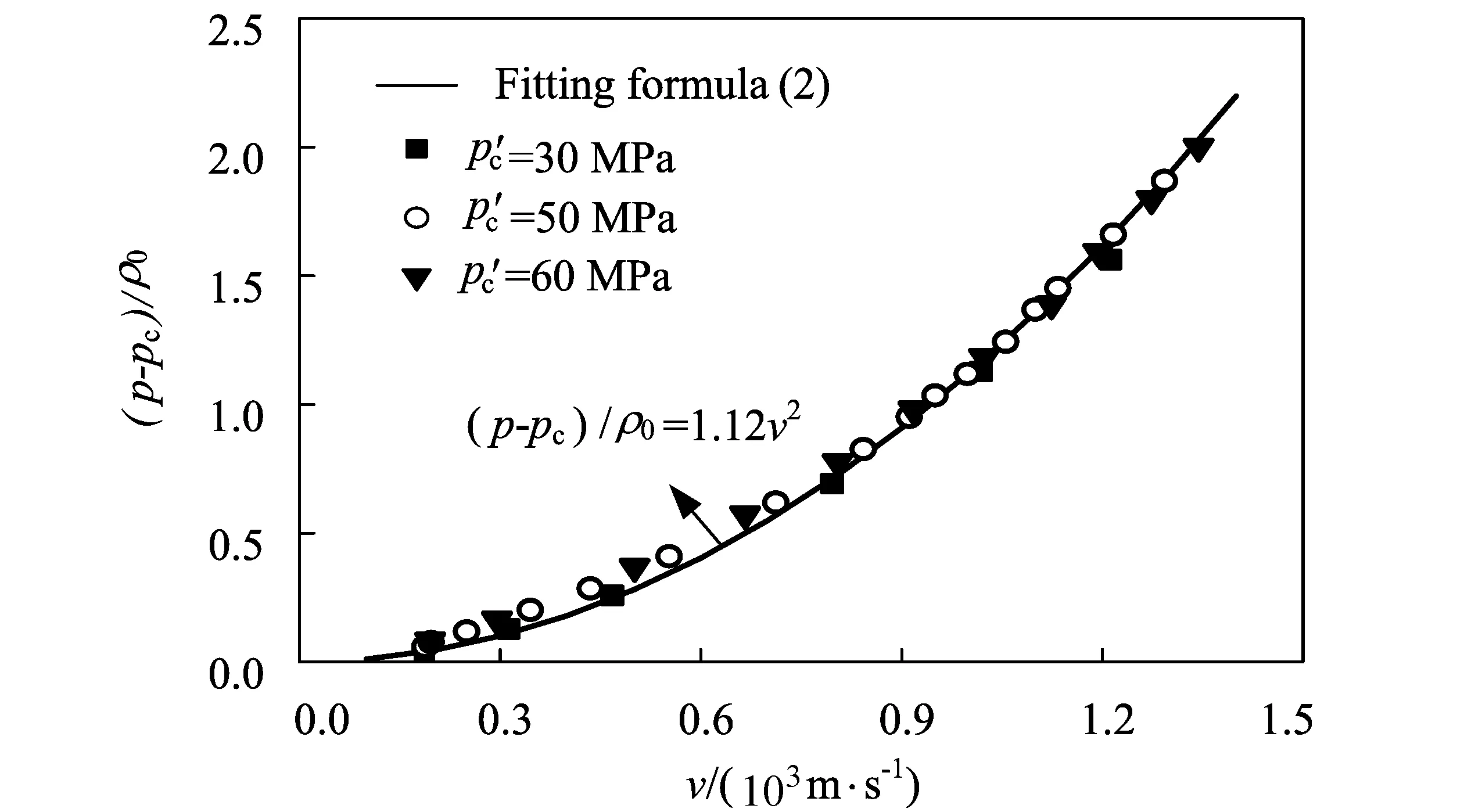
图11 空腔膨胀压力-膨胀速度的数值计算结果与拟合公式Fig.11 The numerical results and fitting formula of cavity pressure-expansion velocity

3.4 拟合结果的验证

将拟合得到的公式带入FORRESTAL[6]的侵彻深度计算公式,可得刚性弹体的侵彻半无限大混凝土靶体的深度H计算公式如下所示：

(3)

式中:m,d,ρ,N分别为弹体的质量、弹体直径、弹体密度和弹头形状因子;v1为侵彻过程开坑阶段结束时的速度,表达式如下所示。

(4)

FREW et al[16]中给出了直径d分别为2.03和3.05 mm,材料分别为4340和AerMet的两种弹体侵彻抗压强度为58.4 MPa混凝土的实验数据。将通式(3)的计算结果与实验数据作对比,如图12所示。图中实验值略大于本文公式的预测值,分析如下:

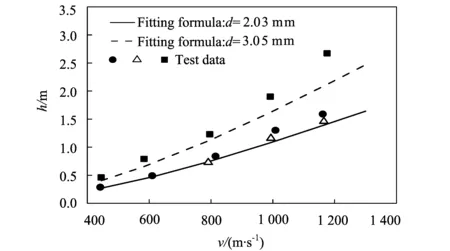
图12 计算侵彻深度与实验数据的对比Fig.12 Comparison of penetration depths between the fitting formulas and experiments

1) 本文推导的公式是基于FORRESTAL理论的结论,FORRESTAL理论对开坑深度的估计值偏小,进而会导致对整体侵彻深度的估计偏小。

2) 按照FORRESTAL的理论,均认为pc的取值应对应与空腔边界膨胀的速度达到稳定值,但在实际侵彻过程不能保证弹道周围靶体材料膨胀速度都达到了稳定值,因此过大地估计了弹体所受到的阻力,因此使侵彻深度预测值偏小。虽有误差,但计算结果仍然与实验数据基本保持一致,验证了本文采用球形动态空腔膨胀模拟方法的正确性,同时也验证了拟合得到的计算公式的适用性。

4 结论

采用LS-DYNA对混凝土材料三维动态球形空腔膨胀的数值模拟,表明空腔界面压力与膨胀速度平方成正比,密度与膨胀速度平方成反比,且膨胀速度随抗压强度的提高而降低;而空腔初始半径,及混凝土材料的抗拉强度和剪切模量等对空腔界面的膨胀速度基本没有影响。通过将膨胀过程中模型径向应力分布情况与空腔膨胀理论计算数值进行对比,二者基本保持一致,证明了该模拟方法的可靠性。根据数值计算结果通过引入无量纲修正系数,得到了混凝土空腔膨胀速度达到稳定值并持续膨胀对应的临界压力的计算公式。同时拟合得到了混凝土材料空腔界面压力与其膨胀速度的函数关系,并将公式与侵彻模型结合,得到侵彻深度的计算公式。通过与实验数据的对比,验证了模拟方法的正确性,同时也表明侵彻深度计算公式是适用的。

[1] BISHOP R F,HILL R,MOTT N F.The theory of indentation and hardness test[J].Proc Phys Soc,1945,57(3):147-159.

[2] HILL R.The mathematical theory of plasticity[M].Oxford:Oxford University Press，1952,2:97-114.

[3] GOODIER J N.On the mechanics of indentation cratering in solid targets by impact of hard and soft spheres[J].Seventh symposium on hypervelocity,1965,3:215-219.

[4] FORRESTAL M J,LUK V K.Dynamic spherical cavity expansion in a compressible elastic-plastic solid[J].Journal of Applied Mechanics,1988,55:275-279.

[5] LUK V K,FORRESTAL M J,AMOS D E.Dynamic spherical cavity expansion of strain-hardening materials[J].Journal of Applied Mechanics,1991,58(1):1-6.

[6] FORRESTAL M J,ALTMAN B S,CARGILE J D,et al.An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J].Int J Impact Engng,1994,15(4):395-405.

[7] FORRESTAL M J,TZOU D Y.A spherical cavity expansion penetration model for concrete targets[J].Int J Solids Struct,1997,34(31/32):4127-4146.

[8] 王延斌,李九红,魏雪英,等.高速钨杆弹对脆性靶体的侵彻分析 [J].高压物理学报,2005,19(3):257-263.

[9] 黄民荣,顾晓辉,高永宏.基于Griffith强度理论的空腔膨胀模型与应用研究[J].力学与实践,2009,31(5):30-34.

[10] 王一楠,黄风雷.混凝土材料动态球形空腔膨胀的数值模拟[J].北京理工大学学报,2010,30(1):5-9.

[11] 李志康,黄风雷.混凝土材料的动态空腔膨胀理论[J].爆炸与冲击,2009,29(1):95-100.

[12] 李志康,黄风雷.考虑混凝土孔隙压实效应的球形空腔膨胀理论[J].岩土力学,2010,31(5):1481-1485.

[13] 陈星明,刘彤,肖正学.混凝土HJC模型抗侵彻参数敏感性数值模拟研究[J].高压物理学报,2012,26(3):313-318.

[14] 巫绪涛,李耀,李和平.混凝土HJC本构模型参数的研究[J].应用力学学报,2010，27(2):340-344.

[15] LSTC.LS-DUNA keyword user’s manual version 971[M].California:Lstc,2007:673-682.

[16] FREW D J,HANCHAK S J,GREEN M L,et al.Penetration of concrete targets with ogive-nose steel rods[J].Int J Impact Eng,1998,21(5):489-497.

(编辑：朱 倩)

Numerical Study on the Dynamic Spherical Cavity Expansion of Concrete Materials

JIN Xiaochao,YANG Huawei,WANG Zhihua,SHU Xuefeng

(InstituteofAppliedMechanicsandBiomedicalEngineering,TaiyuanUniversityofTechnology,Taiyuan, 030024,China)

To study the influence factors of the dynamic spherical cavity expansion,a series of numerical simulations of concrete materials were performed by using LS-DYNA. Numerical results show that the cavity wall expansion velocity squared is proportional to the pressure on the cavity wall, is inversely proportional to the density, and expansion velocity decreases with the increase of the unconfined compression strength, while the initial radius of the cavity and the tensile strength of concrete are independent of the expansion velocity of the cavity wall. The distribution of the radial stress in the simulation model has a good agreement with the theoretical computation for the compressible concrete materials. The fitting formula of the critical pressure that can ensure the cavity expansion velocity to reach a constant was proposed. In addition, the function between the pressure inside the spherical cavity and the expansion velocity was established on the basis of the numerical results. Finally, the equations were proposed to calculate the penetration depth for concrete target. The fitting formulas were validated by the experimental data.

concrete;spherical cavity expansion;critical pressure;penetration depth;numerical study

1007-9432(2016)03-0405-06

2015-08-25

国家自然科学基金资助项目:强动载荷下碳纤维增强复合夹芯结构的动力行为及其吸能机理研究(11390362),强冲击载荷下钢筋混凝土的本构关系、破坏机理与数值方法(11172195);山西省青年科技研究基金:焊接工艺参数对金属间化合物力学性能及焊点可靠性的影响研究(2015021017)

晋小超(1990-),男,湖北十堰人，硕士生,主要从事冲击动力学研究,(E-mail)jinxiaochaotyut@163.com

树学峰,教授,博导,主要从事冲击动力学研究,(E-mail)shuxuefeng@tyut.edu.cn

O385.1

A

10.16355/j.cnki.issn1007-9432tyut.2016.03.024