氟化氢团簇（HF）n（n＝2～8）拓扑性区别氢键构型的图论列举法和量子化学计算法研究

买合木提江·杰力，阿布来提·麦麦提，阿里木江·艾拜都拉，买买提·吐尔逊

（1.喀什大学化学与环境科学学院，2.新疆特色药食用植物资源化学重点实验室，3.物理与电气工程学院，喀什844006）

氟化氢团簇（HF）n（n＝2～8）拓扑性区别氢键构型的图论列举法和量子化学计算法研究

买合木提江·杰力1，2，阿布来提·麦麦提3，阿里木江·艾拜都拉1，买买提·吐尔逊1，2

（1.喀什大学化学与环境科学学院，2.新疆特色药食用植物资源化学重点实验室，3.物理与电气工程学院，喀什844006）

利用提出的图论程序列举出氟化氢团簇（HF）n（n＝2～8）所有可能存在的拓扑性区别氢键构型，通过精密调查获得有可能存在的拓扑性区别构型，发现了满足HF团簇稳定性的若干条件，在这些条件的基础上编写FORTRAN程序和Python语言执行程序，再用画图软件包GraphViz2.37自动画出对应的有向图或条件性有向图.以对应的有向图作理论框架，分别利用从头算法Moller⁃Plesset（MP2）二级微扰方法和密度泛函理论（DFT）方法B3LYP计算水平的6⁃31G∗∗（d，p）基组对氟化氢团簇（HF）n（n＝3～7）所有拓扑性区别条件性有向图对应的初始结构进行结构优化并作振动频率分析，获得氟化氢团簇（HF）n（n＝2～7）的最稳定构型，发现了氟化氢团簇的五聚体（HF）5、六聚体（HF）6和七聚体（HF）7等一些新的稳定结构.

氟化氢团簇；图论列举法；氢键矩阵；有向图；拓扑性区别；量子化学计算

通过氢键作用形成的氢键团簇在许多化学和生物过程中具有重要意义.研究氢键团簇的形成、结构和性质及演化过程，不仅可在原子与分子物理和凝聚态物理之间架起一座桥梁，而且对于发展原子、分子间相互作用理论和氢键理论、生命科学、材料科学、表面科学、催化反应动力学、生命科学及环境科学等都具有重要意义.氢键团簇是近几十年来的研究热点，溶解、能量转移、生物体中各种生物化学反应和有机及无机化学反应都离不开氢键的作用，无论是在理论上还是在实验上对氢键的研究都很多报道［1，2］.近几十年来，随着有关气相中氟化氢团簇的结构和热力学性质研究［3，4］的开展，越来越多的科学家对氟化氢团簇予以了广泛关注.如利用电子衍射法研究了偏离理想气体的性质［5，6］、热容量［7］和光谱特征［8，9］.此外，对氟化氢团簇还进行了从头计算分子轨道计算法研究［10～13］、密度泛函理论计算法研究［10］、分子动力学（MD）模拟［14，15］和蒙特卡洛模拟研究［16］等，研究范围主要涉及到尺寸不同氟化氢团簇的振动光谱振动频率、势能表面曲线、稳定结构［10～16］和热力学性质［13］等.（HF）n作为已知原子数最少的氢键体系，具有很大的自缔能力，选择（HF）n为氢键体系研究氢键团簇模型有助于人们更深入地了解氢键的本质.

图是表示一定分子或分子团簇拓扑学特性的一种数学结构.人们应用图论研究了烷烃的热力学性质［17］、芳香烃的π电子能量［18］等各种分子的不同性质，还利用图论技术研究过（H2O）8，（H2O）20，H＋（H2O）8和H＋（H2O）20［19］；我们［20～23］曾研究列举过水团簇和质子化水团簇所有可能存在的拓扑性区别氢键构型.虽然研究者从实验和理论上研究测定了不同凝聚相中不同尺寸的氟化氢团簇及其质子化团簇体系的振动光谱、电离能、热力学性质［8，9，13］，理论研究也从不同角度研究过这些氟化氢团簇体系［10～16］，但是这些研究没有阐明所有可能存在的拓扑性构型，也没有系统地导出拓扑性区别稳定团簇及不同稳定构型的振动光谱图和热力学性质.目前尚未发现利用图论技术研究氟化氢团簇的研究报道.

本文提出了一种列举氟化氢团簇（HF）n（n＝2～8）所有可能存在的拓扑性区别构型的算法，将这些列举出的构型当作理论框架，分别利用从头算法Moller⁃Plesset二级微扰方法（MP2）的6⁃31G∗∗（d，p）和密度泛函理论（DFT）方法B3LYP计算水平的6⁃31G∗∗（d，p）基组对氟化氢团簇（HF）n（n＝2～5）和所有可能存在的拓扑性区别初始结构进行结构优化，并获得拓扑性区别稳定结构，选取了氟化氢团簇的稳定氢键构型满足的一些结构条件，并将这些条件运用于中等尺寸氟化氢团簇（HF）n（n＝5～7）获得了所有可能存在的稳定构型.

1 理论基础和计算方法

1．1 图和邻接矩阵

根据数学概念，图是顶点和边的集合.图有对应的矩阵，即邻接矩阵表示式.邻接矩阵A＝（aij）为顶点之间相邻关系的矩阵.当顶点i和j通过边连接时，邻接矩阵元素aij＝1，若相反，则aij＝0.分子结构可以用图来表示［11］.如氟化氢团簇三聚体（HF）3的结构（图1），图1中1个顶点相当于1个氟化氢分子，边相当于2个氟化氢分子之间的氢键.氟化氢团簇三聚体（HF）3对应的图可以表示3个分子中氢键连接情况.

Fig．1 Structure of a hydrogen⁃bonded HF cluster trimer（A）with the equivalent graph（B）and the corresponding adjacency matrix（C）

1.2 有向图和氢键矩阵

根据有关数学概念有向图是顶点和弧的集合，弧是有方向的边，通常用箭头来表示.如三聚氟化氢团簇（图2）中氟化氢分子通过有方向性的氢键相互连接，此处，方向性表示2个氟化氢分子之间的给⁃受质子的关系.氟化氢团簇中的氢键构型可以用有向图来表示.

Fig．2 Structure of a hydrogen⁃bonded HF cluster trimer with the equivalent digraph and the corresponding hydrogen⁃bond matrix

由图2可见，氟化氢团簇结构中的1个氟化氢分子相当于有向图的顶点，从给予体氟化氢分子到接受体氟化氢分子的氢键相当于有向图中的箭头.与图一样有向图也有对应的矩阵表示式，这种矩阵式称为氢键矩阵（简称HB矩阵）［24］.一个HB矩阵H＝（hij）的元素hij取值：当氟化氢分子i向另一个氟化氢分子j给予质子（提供氢键）时，hij＝1，否则hij＝0.

每个有向图相当于1个氟化氢分子团簇氢键构型，而这些有向图需要满足若干条件.在1个HF分子团簇中1个HF分子有从其它HF分子接受3个质子的可能性，同时它把一个质子可以共享给其它2个HF分子.通过HB矩阵可以列举满足上述构成HF分子团簇条件的所有可能存在的拓扑性区别有向图，通过这些有向图获得所有可能存在的拓扑性区别氢键构型.根据上述算法编写的FORTRAN程序列举出的（HF）n（n＝2～8）的图总数和有向图总数列于表1.

Table 1 Numbers of graphs，digraphs，and restrictive digraphs of HF clusters（HF）n（n＝2—8）and the number of stable structures of HF clusters（HF）n（n＝2—7）under the calculation method of MP2／6⁃31G∗∗（d，p）

1.3 条件性有向图和条件性氢键构型

对列举出的所有氟化氢团簇（HF）n，每个拓扑性区别氢键构型设计出不同的初始几何构型.通过分子轨道从头算方法的MP2／6⁃31G∗∗（d，p）或B3LYP／6⁃31G∗∗（d，p）计算水平对每个几何构型进行几何结构优化计算.由表1可见，虽然随着氟化氢团簇体系中HF分子数的增加，HF团簇可能存在的氢键构型迅速增加，但是其中的稳定构型非常少，如通过对氟化氢团簇三聚体的5个有向图（可能存在的氢键构型）、氟化氢团簇四聚体的27个有向图和氟化氢团簇五聚体的247个有向图对应的初始结构的计算，分别发现了2个、2个和4个稳定结构.通过以上结果和前期研究结果［25～38］，总结出了氟化氢团簇的稳定氢键构型对应的有向图需满足的3种结构条件：（1）指向一个顶点的箭头数最多等于2；（2）从一个顶点出来的箭头数可以等于1或2，不能等于零；（3）某个顶点从邻近的其它顶点接受2个箭头时，这个顶点向其它顶点可以提供2个箭头，否则，它不能向其它顶点提供2个箭头.

根据上述条件为基础的算法编写了另一套新的FORTRAN程序，执行该程序移除了所有可能存在的有向图中不能满足上述3个条件的有向图，剩余有向图为条件性有向图，对应这些条件性有向图的氢键构型为条件性氢键构型.列举所有可能存在的拓扑性区别氢键构型和拓扑性区别条件性氢键构型的算法和程序已有详细解释［24］.按编写的FORTRAN语言程序组列举出所有氟化氢团簇（HF）n（n＝2～8）可能存在的有向图和条件性有向图对应的HB矩阵，然后利用编写的Python语言程序，在画图软件包GraphViz2.37［39］中自动画出对应的有向图或条件性有向图.

探索中等尺寸氟化氢分子（HF）n（n＝5～7）团簇稳定结构时，条件性氢键构型提供比较理想的初始结构.

1.4 每个稳定构型对应于一个HB矩阵

用计算化学图形工具软件Chem Office Ultra1 2.0［40］和GaussView 5.0［41］分别对上述步骤列举出的每个拓扑性区别氟化氢团簇（HF）n（n＝2～6）条件性有向图设计出不同的最初几何构型.利用Gaussian 09程序［42］进行分子轨道从头算法MP2／6⁃31G∗∗（d，p）和密度泛函理论方法的B3LYP／6⁃31G∗∗（d，p）计算水平对每个几何构型进行几何结构优化计算，对获得的每个优化结构进行振动频率分析并保证没有虚频.需要强调的是，最后得到的稳定构型对应于一个有向图（或条件性有向图），每个稳定构型对应的这个有向图（或条件性有向图）对应于唯一的某个HB矩阵.

2 结果与讨论

（HF）n（n＝2～8）团簇图、有向图和条件性有向图总数与对应的稳定结构列于表1.需要强调的是，本文只研究了拓扑性区别的几何构型，即不考虑团簇几何结构中自由H—F共价键位置区别等任何精细结构.

由图3可见，具有3个顶点的氟化氢团簇三聚体分别有2个图和5个有向图，通过MP2／6⁃31G∗∗（d，p）和B3LYP／6⁃31G∗∗（d，p）水平计算后，从5个有向图对应的5个可能存在的拓扑性区别氢键构型中发现了2个稳定构型.对有4个顶点的氟化氢团簇四聚体，通过计算从27个有向图对应的27个可能存在的拓扑性区别氢键构型中发现了2个稳定构型.（HF）n（n＝5，6）团簇条件性有向图见图4.（HF）n（n＝2～7）团簇优化构型及其对应的有向图见图5.

Fig．3 All the enumerated possible topology⁃distinct graphs and digraphs with n vertices for（HF）n（n＝2—4）The designated patterns（2A，3A，3B，4A and 4B）correspond to the stable structures.

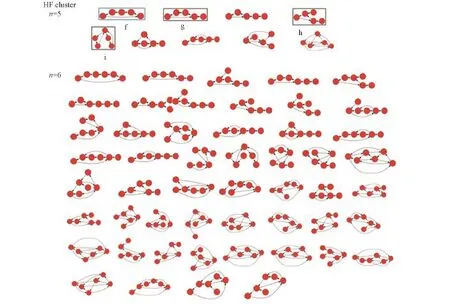
Fig．4 Enumerated restrictive digraphs generated from H⁃B matrices by Python program and GraphViz 2．37 program package corresponding to HF pentamer and hexamerThe designated patterns（f，g，h and i）correspond to the stable structures.

Fig．5 Digraphs and the optimized geometries of HF clusters（HF）n（n＝2—7）

对氟化氢团簇三聚体最稳定的构型是三角形环状结构c，与另一个线形稳定构型b的总能差为34.36 kJ／mol.对于HF四聚体，最稳定的是四角形环状构型（图5中的构型d），与另一个稳定构型e的总能差为51.83 kJ／mol.计算获得的HF团簇的三聚体和四聚体稳定结构（图3中的2A，3A，3B，4A和4B）和五聚体稳定结构（图4和图5的构型f，g，h和i）的拓扑性与通过Monte Carlo模拟和分子模拟方法［16］、从头算法［34，43～46］和DFT计算法［43］等所得的结构相似.

与水团簇四聚体相比，列举出的HF团簇四聚体可能存在的拓扑性区别氢键构型数多于水团簇四聚体［20，21］，但稳定构型数少于水团簇四聚体.

从表1可见，随着氟化氢团簇体系中HF分子数的增加，从HF团簇五聚体开始，可能存在的氢键构型迅速增加，对这么多的初始结构进行计算搜索稳定构型非常难，本文对中等尺寸氟化氢团簇（HF五聚体、六聚体和七聚体）先列举出了条件性拓扑性区别氢键构型，然后对每个氟化氢团簇拓扑性区别条件性氢键构型设计出不同的最初几何构型，并进行结构优化计算.

对HF五聚体，从247种可能存在的有向图中列举了9个条件性有向图，然后对每个拓扑性区别条件性有向图设计出对应这些有向图的不同最初几何构型，并进行结构优化计算，获得了4个稳定构型.对于HF五聚体，最稳定构型的是五角环状构型（图5的构型f）具有C5h对称性，此构型拓扑性相似于文献［15，38～42］报道的最稳定结构.在MP2／6⁃31G∗∗（d，p）计算水平下，构型f与其它稳定构型g，h与i的总能差分别为29.12，69.87和50.00 kJ／mol.氢键最弱且稳定性最差的是带有2个尾巴的三角形构型（图4的构型h）.列举出的HF团簇五聚体可能存在的拓扑性区别氢键构型数多于水团簇五聚体［20～21］，但稳定构型数少于水团簇五聚体［21］.计算获得的HF团簇五聚体稳定结构（图5的构型g，h和i）都具有Cs对称性.通过计算发现了（HF）5团簇的1个新的稳定结构（图4的构型i），即5个氟化氢分子构成2个三角形，中间的氟化氢把1个质子分别与2个相邻氟化氢共享而形成2个氢键的特殊构型.

对HF团簇六聚体，从3272种可能存在的有向图中列举了51个条件性有向图，通过对51个条件性有向图对应的初始结构在MP2／6⁃31G∗∗（d，p）和B3LYP／6⁃31G∗∗（d，p）计算水平下进行优化计算获得了8种稳定结构（图5中结构式6A～6H）.对于HF六聚体，最稳定的构型是六角环状构型（图5的构型6A），具有C6h对称性，此构型拓扑性的角度与蒙特卡洛模拟和分子动力学模拟法［6］、从头算法研究［20，34］中报道的最稳定结构相似.此外，还发现了HF团簇六聚体（HF）6的2个新的稳定构型（图5中的构型6G和6H），其中构型6G的结构是由6个氟化氢分子构成的1个三角形和1个四角形连接而形成的、中间的氟化氢把1个质子分别与2个相邻氟化氢共享形成2个氢键的特殊结构.构型6H是2个三角形结构上连接1个单独氟化氢分子，这2个新的稳定构型都含有7个氢键.在MP2／6⁃31G∗∗（d，p）计算水平下，最稳定构型6A与其它稳定构型6B，6C，6D，6E，6F，6G和6H的总能差分别为22.80，53.18，54.94，54.27，94.60，39.46和67.24 kJ／mol.势能最高的构型6F是由6个氢键构成的1个三角形结构中3个顶点上分别连接3个单独HF分子的结构.从表1可知，列举出的氟化氢团簇六聚体可能存在的拓扑性区别构型数比水团簇六聚体可能存在的拓扑性区别构型数［24，25］多3倍以上，但实际存在的拓扑性区别稳定构型只有8个.

对HF七聚体，从55005种可能存在的有向图中列举了320个条件性有向图，通过对320个条件性有向图对应的初始结构在MP2／6⁃31G∗∗（d，p）和密度泛函理论方法的B3LYP／6⁃31∗∗G（d，p）水平下进行几何优化和频率计算分析获得了14种稳定构型.这些稳定构型（图5构型7A～7N）通过在MP2／6⁃31G∗∗（d，p）水平上计算的总势能（E，eV）和相对总势能（ΔE，eV）列于表2.这14种构型中能量最低的为7个HF构成的七环型结构，此构型与其它用蒙特卡洛模拟和分子动力学模拟法［14］、从头算法研究［20，34］中报道的结构一致.氟化氢团簇七聚体的稳定结构中有七元环结构、六元环上加1个HF分子支链型结构、五元环上加2个HF分子支链结构形成的蝴蝶型结构（5个氟化氢分子形成2个三角形，且2个HF分子分别连接这2个三角形）和3个三元环相互连接结构等（见图5构型7A～7N），14种稳定构型通过能量大小对比可发现七元环状构型最稳定.此外，为了更明确反映（HF）7团簇各中稳定构型相对能量与内部结构之间的关系，给出了各构型的相对能量与稳定结构之间的关系图（见图6）和稳定结构相对势能及氢键数之间的关系图（见图7）.按（HF）7的相对能量与各个稳定结构之间的关系曲线图可见，环状（七分子HF构成的七边形环）结构最稳定.此外随着支链（环外自由的氟化氢分子）数的增加，氟化氢团簇七聚体（HF）7的稳定性减弱，大环形结构比小环形结构更稳定.随着氟化氢团簇七聚体（HF）7构型中小环形单元（三元环或四元环）的增加，团簇体系的能量升高、稳定性减弱.图7表明，（HF）7的分子团簇中最稳定的是氢键数为7的七元环结构，稳定性最弱的是3个三元环结构，可见，随着支链（环外自由的氟化氢分子）数的增加，氢键数也增加，氟化氢团簇七聚体（HF）7体系的能量升高，相应构型的稳定性减弱，有9个氢键的3个相连的三元环型构型最不稳定，即随着氟化氢团簇七聚体（HF）7体系结构上支链数和氢键数目的增多，氟化氢团簇七聚体体系的稳定性减弱.

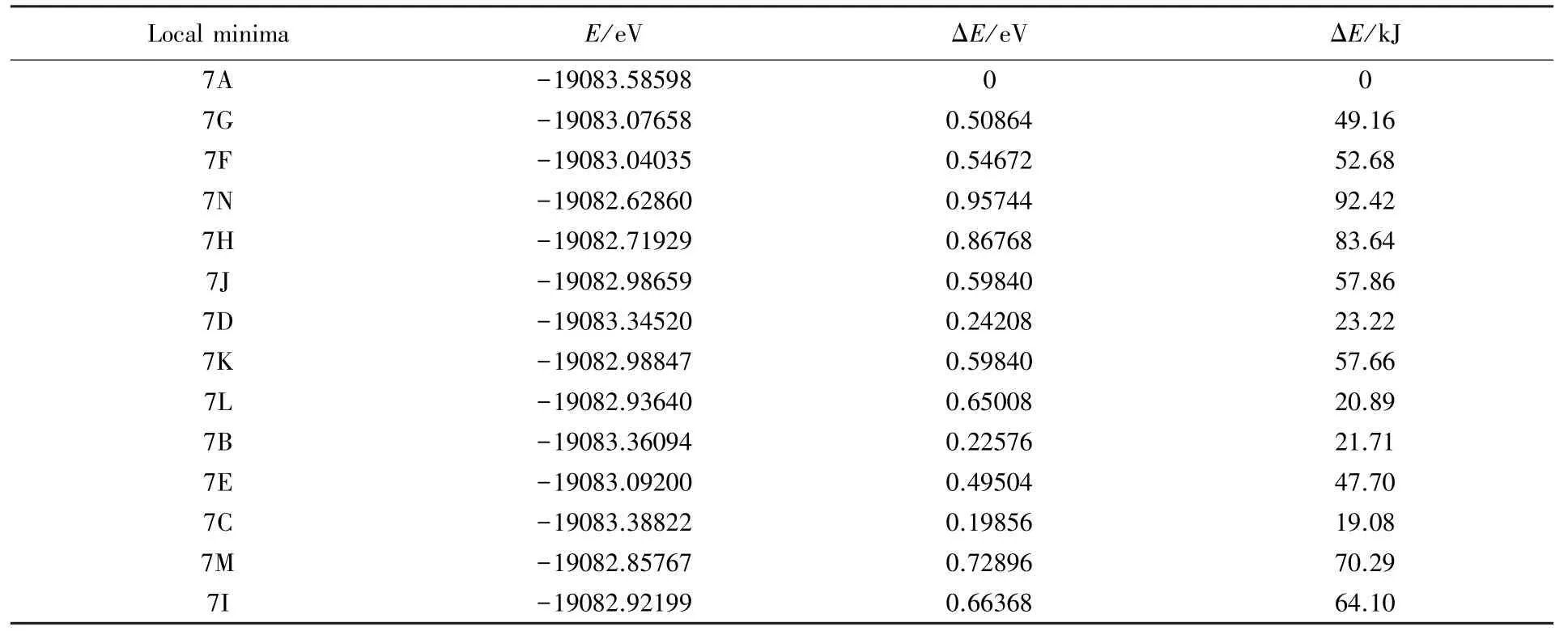
Table 2 14 local minima and corresponding total energy and relative total energy of the（HF）7clusters［MP2／6⁃31G∗∗（d，p）］

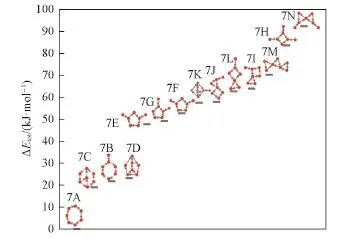
Fig．6 Relative energy of the local minima of（HF）7with the calculation method of MP2／6⁃31G∗∗（d，p）

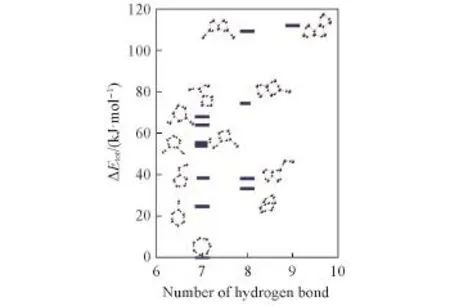
Fig．7 Relative energy and the numbers of hydrogen bond of the local minima of（HF）7with the calculation method of B3LYP／6⁃31G∗∗（d，p）

3 结 论

通过FORTRAN程序分别列举出氟化氢团簇（HF）n（n＝2～8）所有可能存在的拓扑性区别构型，将这些氢团簇（HF）n（n＝2～7）构型当作理论框架，用GaussView5.0和ChemBioOffice等分子结构图形化软件分别做出初始结构，利用MP2／6⁃31G∗∗（d，p）和B3LYP 6⁃31G∗∗（d，p）计算水平分别对氟化氢团簇的1个二聚体（HF）2、5个三聚体（HF）3、27个四聚体（HF）4、247个五聚体（HF）5、51个六聚体（HF）6和320个七聚体（HF）7的初始结构进行结构优化计算.并进行振动频率分析，从而分别获得了氟化氢团簇二聚体（HF）2的1个稳定构型、三聚体（HF）3的2个稳定构型、四聚体（HF）4的2个稳定构型、五聚体（HF）5的4个稳定构型、六聚体（HF）6的8个稳定构型和七聚体（HF）7的14个稳定构型.选取了氟化氢团簇的稳定氢键构型满足的一些结构条件，将这些条件运用于中等尺寸氟化氢团簇（HF）n（n＝5～7）获得了所有可能存在的稳定构型，发现了氟化氢团簇五聚体、六聚体和七聚体等一些新的稳定构型.

［1］ Aakerðy C.B.，Seddon K.R.，Chem．Soc．Rew.，1993，22（6），397—407

［2］ Scheiner S.，Molecular Interactions from van der Waals to Strong Bound Complexes，John Wiley＆Sons Lid.，Chichester，1997，25—97

［3］ Redington R.L.，J．Phys．Chem．，1982，86，552—560

［4］ Curtis L.A.，Blander M.，Chem．Rev．，1988，88，827—841

［5］ Wang R.W.，Hildeb J.H.，Morell W.E.，J．Am．Chem．Soc．，1943，65，182—187

［6］ Briegleb G.，Strohmeier W.，Z．Elektrochem．，1953，57，668—674

［7］ Frank U.，Meyer F.，Z．Elektrochem．，1959，63，571—578

［8］ Barnes A.J.，Hallan H.E.，Jones D.，Proc．R．Soc．London，Ser．A，1973，335，97—104

［9］ Smith D.F.，J．Chem．Phys．，1958，28，1040—1047

［10］ Yulia N.，Struct．Chem．，2012，23，1253—1266

［11］ Almeida T.S.，Cabral B.J.C.，J．Chem．Phys．，2010，132，094307

［12］ Bai X.，Ming N.，Brown R.E.，J．Phys．Chem．A，2011，115，10596—10599

［13］ Sophy K.B.，Kuo J.L.，J．Chem．Phys．，2009，131，224307

［14］ Swalina C.，Wang Q.，Chakraborty A.，Hammes⁃Schiffer S.，J．Phys．Chem．A，2007，111，2206—2212

［15］ Sun H.，Watts R.O.，Buck U.，J．Chem．Phys．，1992，96，1810—1821

［16］ Zhang C.，Freeman D.L.，Doll J.D.，J．Chem．Phys．，1989，91，2489—2497

［17］ Hosoya H.，Gotoh M.，Murakami M.，Ikeda S.，J．Chem．，Inf．Comput．Sci．，1999，39，192—196

［18］ Gutman I.，Soldatovic′T.，Vidovic D.，Chem．Phys．Lett．，1998，297，428—432

［19］ McDonald S.，Ojamae L.，Singer S.J.，J．Phys．Chem．A，1998，102，2824—2832

［20］ Miyake T.，Aida M.，Chem．Phys．Lett．，2002，363，106—110

［21］ Miyake T.，Aida M.，Internet Electron．J．Mol．Des．，2003，2，24—32

［22］ Jieli M.，Miyake T.，Aida M.，Bull．Chem．Soc．Jpn．，2007，80（11），2131—2136

［23］ Jieli M.，Aida M.，J．Phys．Chem．A，2009，113，1586—1594

［24］ Jelil M.，Abaydulla A.，J．Chem．Phys．，2015，143，044301

［25］ Alfred K.，Int．J．Q．Chem．，2004，38（S24），129—140

［26］ Curtis L.A.，Blander M.，Chem．Rev．，1988，88，827—841

［27］ Sun H.，Watts R.O.，Buck U.，J．Chem．Phys．，1992，96，1810—1821

［28］ Zhang C.，Freeman D.L.，Doll J.D.，J．Chem．Phys.，1989，91，2489—2497

［29］ Quack M.，Suhm M.A.，J．Chem．Phys．，1991，95，28—59

［30］ Klopper W.，Quack M.，Suhm M.A.，J．Chem．Phys．，1998，108，10096—10115

［31］ Grigorenko B.L.，Nemukhin A.V.，Apkarian V.A.，J．Chem．Phys．，1998，108，4413—4425

［32］ Ovchinnikov M.，Apkarian V.A.，J．Chem．Phys.，1999，110，9842—9852

［33］ Guedes R.C.，DoCouto P.C.，Costa Cabral B.J.，J．Chem．Phys．，2003，118，1272—1281

［34］ Luis R.，Rafael A.，David G.A.，Helena D.R.，J．Chem．Phys.，2001，114，5552—5561

［35］ Michael W.A.，Philip T.G.，Curottoa E.，J．Chem．Phys．，2006，124，174305

［36］ Howard B.J.，Dyke T.R.，Klemperer W.，J．Chem．Phys．，1984，81，5417—5423

［37］ Pine A.S.，Howard B.J.，J．Chem．Phys．，1986，84，590—596

［38］ Yukhnevich G.V.，Tarakanova E.G.，Nemukhin A.V.，Russian．Chem．Bull．，1997，46，414—422

［39］ Arif B.，GraphViz，Version 2.38，AT＆TLabs，Inc.，Austin，2014

［40］ ChemBio Office Ultra，Version 12.0，Cambridge Soft Corporation，Software Publishers Association，Washington DC.，2010

［41］ Dennington，Keith T.，Millam J.，GaussView，Version 5，Semichem Inc.，Shawnee Mission，KS，2009

［42］ Frisch M.J.，Trucks G.W.，Schlegel H.B.，Scuseria G.E.，Robb M.A.，Cheeseman J.R.，Scalmani G.，Barone V.，Mennucci B.，Petersson G.A.，Nakatsuji H.，Caricato M.，Li X.，Hratchian H.P.，Izmaylov A.F.，Bloino J.，Zheng G.，Sonnenberg J.L.，Hada M.，Ehara M.，Toyota K.，Fukuda R.，Hasegawa J.，Ishida M.，Nakajima T.，Honda Y.，Kitao O.，Nakai H.，Vreven T.，Montgomery J.A.，Peralta J.E.，Ogliaro F.，Bearpark M.，Heyd J.J.，Brothers E.，Kudin K.N.，Staroverov V.N.，Kobayashi R.，Normand J.，Raghavachari K.，Rendell A.，Burant J.C.，Iyengar S.S.，Tomasi J.，Cossi M.，Rega N.，Millam J.M.，Klene M.，Knox J.E.，CrossJ.B.，Bakken V.，Adamo C.，Jaramillo J.，Gomperts R.，Stratmann R.E.，Yazyev O.，Austin O.A.J.，Cammi R.，Pomelli C.，Ochter⁃ski J.W.，Martin R.L.，Morokuma K.，Zakrzewski V.G.，Voth G.A.，Gaussian 09，Revision A．02，Gaussian Inc．，Wallingford CT，2009

［43］ Abu⁃Awwad F.M.，Chem．Phys．Lett.，2002，360，340—348

［44］ Friedrich J.，Perlt E.，Roatsch M.，Spickermann C.，Kirchner B.，J．Chem．，Theory Comput．，2011，7，843—851

［45］ Muller H.，Franke R.，Vogtner S.，Jaquet R.，Kutzelnig W.，Theor．Chem．Acc．，1998，100，85—102

［46］ Andrews L.，Bondybev V.E.，English J.H.，J．Chem．Phys.，1984，81，3452—3457

（Ed.：Y，Z，S）

†Supported by the National Natural Science Foundation of China（No.21363010）and the Kashgar University Research Key Program Founda⁃tion，China（No.132457）.

Investigation of Topology⁃distinct Stable Structures for Hydrogen Fluoride Clusters（HF）n（n＝2—8）by the Methods of Graph Theoretical Enumerations and Quantum Chemical Calculations†

MAHMUTJAN Jelil1，2，ABLAT Mamat3∗，ALIMJAN Abaydulla1，MAMAT Tursun1，2
（1．College of Chemistry and Environmental Science，2．Key Laboratory of Xinjiang Native Medicinal and Edible Plant Resources Chemistry，3．College of Physics and Electrical Engineering，Kashgar University，Kashgar 844006，China）

A graph theoretical procedure to generate all the possible topology⁃distinct structures for hydrogen fluoride（HF）clusters was presented and all the possible topology⁃distinct structures for hydrogen fluoride（HF）n（n＝2—8）clusters were enumerated in this work.On the basis of the restrictions found，FORTRAN program was designed and executed by Python program，and the corresponding diagraphs or restrictive digraphs were drawn by means of free graph visualization software，GraphViz 2.38 for HF cluster（HF）n（n＝2—8）.Within the theoretical framework of the corresponding digraphs or restrictive digraphs，all the topology⁃distinct local minima for（HF）n（n＝3—7）were optimized and analyzed by means of ab initio method and density functional theory（DFT）method at the level of MP2／6⁃31G∗∗（d，p）and B3LYP／6⁃31G∗∗（d，p），respectively.The local minimum structures for（HF）n（n＝3—7）are the same as those in the previous works.For HF pentamer，hexamer and heptamer，some new local minimum structures were obtained.

Hydrogen fluoride cluster；Graph theoretical enumeration；Hydrogen bond matrix；Digraph；Topology⁃distinct；Quantum chemical calculation

O641

A

10.7503／cjcu20160275

2016⁃04⁃25.网络出版日期：2016⁃11⁃15.

国家自然科学基金（批准号：21363010）和喀什大学重点项目（批准号：132457）资助.

联系人简介：阿布来提·麦麦提，男，讲师，主要从事计算物理方面的研究.E⁃mail：ablet238＠aliyun.com