用于超宽带高分辨率成像的二维稀疏MIMO面阵拓扑结构研究

谭恺 吴世有 王友成 叶盛波 陈洁 方广有

(1.中国科学院电子学研究所，北京 100190;2.中国科学院大学,北京 100039)



用于超宽带高分辨率成像的二维稀疏MIMO面阵拓扑结构研究

谭恺1,2吴世有1王友成1,2叶盛波1陈洁1方广有1

(1.中国科学院电子学研究所，北京 100190;2.中国科学院大学,北京 100039)

分析并总结了超宽带二维多输入多输出(Multiple Input Multiple Output,MIMO)面阵拓扑结构设计的两条原则——等效孔径的均匀性与无明显遮蔽性,并根据这两条原则提出了一种用于超宽带近距离高分辨率成像的新型面阵拓扑结构.与尺寸、阵元数相同的MIMO面阵相比,该新型面阵结构在仿真获取的方向图中具有更好的聚焦效果和旁瓣抑制能力.并且,不同距离下的聚焦结果显示,该面阵的峰值旁瓣水平均要低于另两个阵列2 dB以上.对复杂目标成像的实验结果进一步证明了该阵列良好的成像性能.结合其等效阵元数量较少的特点,文中提出的这种新型MIMO面阵拓扑结构为高效、实时的超宽带近距离高分辨率成像应用提供了可能.

超宽带雷达技术;高分辨率成像;MIMO阵列;二维面阵拓扑结构

DOI 10.13443/j.cjors.2015121701

引 言

超宽带多输入多输出(Multiple Input Multiple Output,MIMO)阵列系统由于能够实现高分辨率和低栅瓣、低旁瓣水平的成像效果而在许多应用中受到了日益广泛的关注.例如,无线监控,机场安检,穿墙探测与救援,医疗诊断,等等.在超宽带MIMO阵列成像系统的应用中,阵列拓扑结构是系统设计中关键的一个环节,这是因为阵元的空间配置对最终的成像结果有直接影响.一个合理设计的面阵拓扑结构,能够提高阵列的旁瓣抑制能力和成像效果,从而提高阵元的使用效率.

利用等效孔径的概念,超宽带MIMO阵列可以转换为单程阵列进行分析和设计[1].通过文献[1]可知,对于一维线阵列而言,若其等效孔径满足均匀、周期且单位加权的排列方式,则该线阵结构即为最优的拓扑结构.据此,文献[2]提出了设计最优的一维线性MIMO超宽带阵列结构的方法.然而,对于二维面阵的设计,情况则要复杂得多,这是因为二维面阵列的辐射特性沿其所在平面内不同角度是不同的,因此难以获得一个通用的设计方法.文献[3]通过改变收发阵元的间距,提出了一种面阵结构设计的框架思路.而后,文献[4-8]分别研究了多种不同的用于超宽带成像的MIMO面阵结构.文献[9]结合射电望远镜系统中传感器阵元的配置方式,提出了一种9发16收的平面螺旋结构.与其他具备相同阵元数的面阵相比,该螺旋结构面阵具有更好的旁瓣抑制能力.然而,到目前为止,并没有一种通过使用较少数量的等效阵元以实现高效、实时成像的面阵结构,因而在该领域仍需要做进一步的研究.

对于某些对实时性要求较高的场合,例如,穿墙动目标跟踪成像,较多的等效阵元虽然在一定程度上可以增加成像结果的动态水平,但同时也大大增加了数据量和处理时间,因而在这些场合下是不合适的.针对该问题,本文分析并总结了关于超宽带二维MIMO面阵设计的两条基本原则,等效孔径的均匀性和无明显遮蔽性,并根据这两条设计原则,提出了一种仅使用4个发射单元和16个接收单元的新型二维面阵拓扑结构.

1 超宽带MIMO面阵设计原则及新型面阵拓扑结构

1.1 基本理论及设计原则分析

宽带阵列系统由于其发射信号具有窄脉冲的特点,目标回波在聚焦时只会在焦点位置及其附近区域内进行相干叠加,该区域被称为相干区域(Interference Region,IR),其角度范围确定如下[10]:

(1)

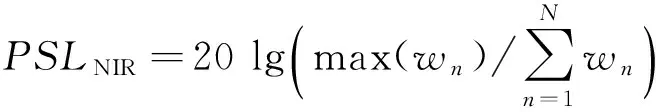
(2)

式中,wn是第n个阵元的权值.

在分析和设计雷达回波阵列系统时,通常需先将其转换为一个单程等效孔径.对于超宽带MIMO阵列而言,等效孔径可以通过式(3)获得[2]:

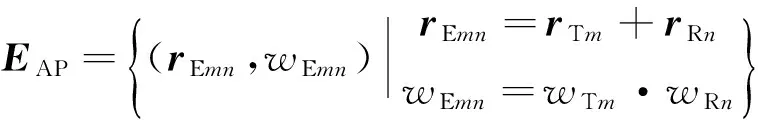
(3)

式中: m=1,…,NT; n=1,…,NR; NT和NR分别是发射阵元的个数和接收阵元的个数; (rTm,wTm)和(rRn,wRn)分别代表第m个发射单元和第n个接收单元的位置及其权值.对于一维线性超宽带MIMO阵列的设计,最优的拓扑结构须能够使其等效阵列具备周期、均匀排列且单位加权的特点,即应满足如下关系[2]:

(4)

式中： ΔT和ΔR分别为发射阵列和接收阵列的采样间隔； Δsub，T和Nsub，T分别为每一个发射子阵中的阵元总数和采样间隔.因此,给定阵列尺寸及阵元个数NT和NR,通过式(4)就可以设计出具有均匀排列、单位加权等效孔径的最优一维线性MIMO阵列拓扑结构.

相对一维线阵列结构设计,二维面阵的情形要复杂许多,这是因为面阵的方向图是其所在二维平面的函数,即面阵的辐射特性沿其所在平面内的不同角度是不相同的.但是,通过切片投影法[11],二维面阵可以等效为一系列的一维线阵,进而分析其不同角度的特性.这里所谓的一维等效线阵是指二维面阵的所有阵元沿某直线的投影,该直线位于面阵所在的平面内,且与x轴的夹角为φ.切片投影法指出,在φ角度下,投影所得一维等效线阵远场(也包括近场焦点附近)的辐射方向图即为此面阵沿该角度的方向图.

通过对上述基本概念的介绍和分析,对于二维超宽带稀疏MIMO面阵结构的设计,应当使其等效孔径沿任意角度的投影都尽量满足均匀、周期排列和单位加权这两个特点,才能使该二维面阵沿各角度都有良好的聚焦性能和旁瓣控制能力.因此,两条基本设计原则可以总结如下:

1) 等效面阵中所有阵元应当均匀地覆盖孔径平面,尽可能少地出现阵元的重叠和冗余,以保证面阵沿各角度投影所得的一维等效线阵都能近似满足均匀、周期排列的特点.该条原则简称为等效孔径的均匀性.

2) 面阵应避免出现严重的阵元遮蔽,以保证沿每个角度投影所得的一维等效线阵都能近似满足单位加权的特点.该条原则简称为等效孔径的无明显遮蔽性.

由上述两条设计原则,在二维面阵结构的设计中,规则排列并不是一个好的选择,它虽然具备良好的均匀性,但其周期、规则的排列方式必然会导致沿某些角度出现严重的阵元遮蔽效应.从这个角度上讲,一个合理的二维面阵拓扑结构,其等效孔径从直观上看应当满足均匀且随机的排列方式.

1.2 新型超宽带MIMO面阵拓扑结构

根据式(3)给出的等效孔径的概念,结合上述

两条超宽带稀疏面阵设计原则,本文提出一种新型的4发16收稀疏MIMO面阵结构,其实孔径和等效孔径如图1(a)(左为实孔径，右为等效孔径)所示阵列1，其向x轴和y轴的投影均为一个2发16收的最优线阵.图中阵元的坐标用中心频率fc=6.0 GHz对应的波长λc=0.05 m为单位进行表示.该拓扑结

(a) 本文提出的面阵(阵列1)

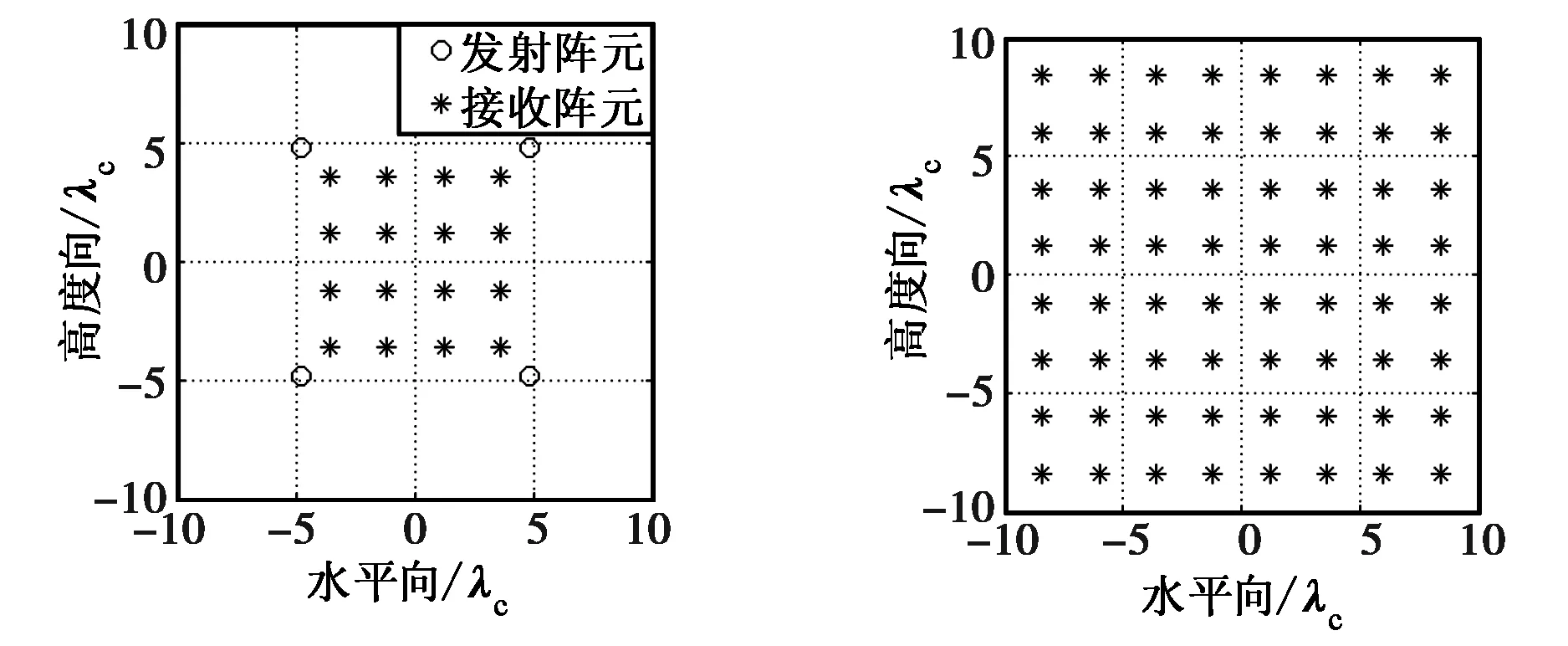
(b) 等效方形面阵(阵列2)

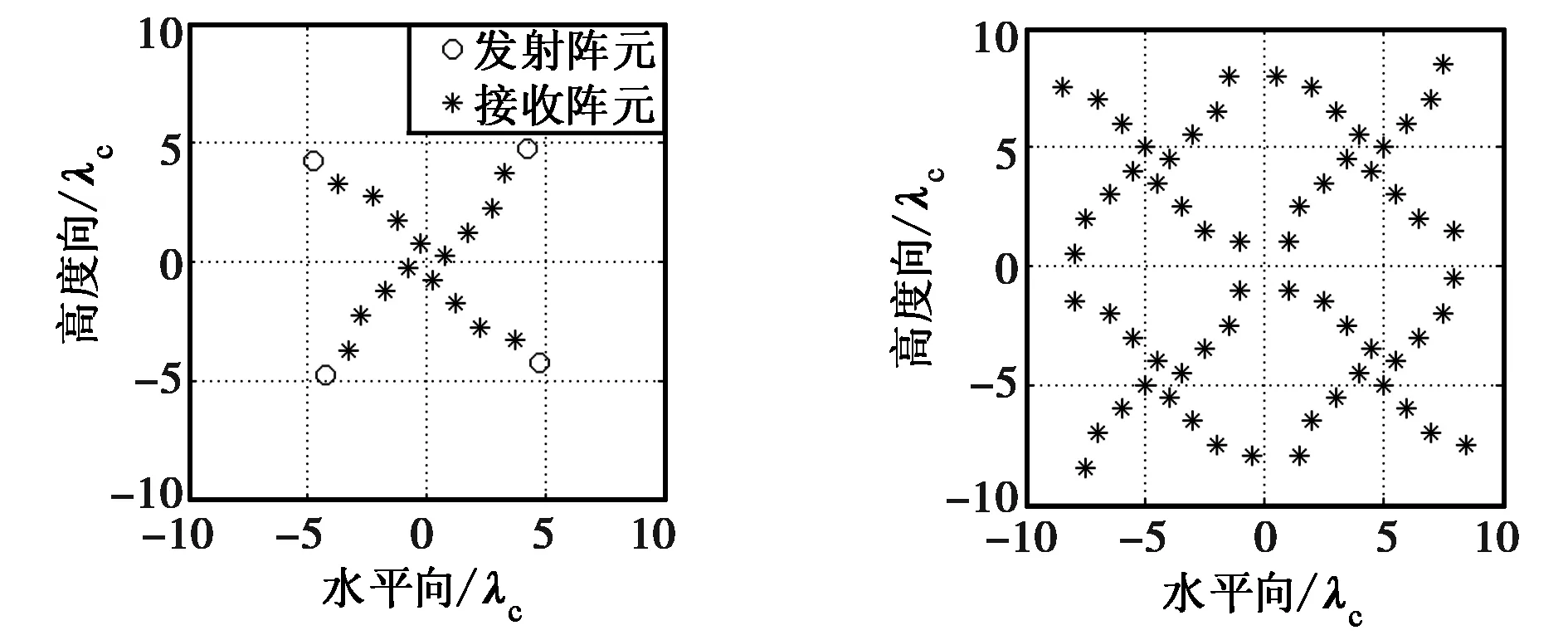
(c)十字型面阵(阵列3)图1 MIMO阵列拓扑结构及其等效孔径

构中,四个发射阵元对称地位于一个宽度为ΔT的正方形四个顶点处,即发射阵列坐标为

(5)

宽度ΔT由成像所需分辨率决定.16个接收阵元全部位于该正方形内部,给定向量

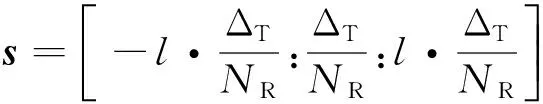
(6)

式中,l=(NR-1)/2.则接收阵列具体坐标

(7)

式(5)和(7)表明该面阵向x轴和y轴的投影都是一个满足式(4)的宽度为ΔT的最优一维线性MIMO阵列,如图1(a)所示.

为了突出该新型面阵良好的聚焦性能及旁瓣抑制能力,本文引入了另外两个被广泛使用的4发16收面阵结构作为对比:等效矩形面阵(阵列2)[9]和十字形面阵(阵列3)[5].它们的MIMO实孔径结构及其对应的等效孔径如图1(b)和(c)所示.为了保证有相同的分辨率,图1中阵列2和3的尺寸与图1(a)中阵列1基本一致.

2 理论与仿真分析

2.1 理论分析

在进行仿真之前,我们通过观察和分析图1中的等效孔径,先对三个阵列的性能做一个初步的判断.首先,三个阵列都拥有尺寸大小近乎一样的等效孔径,这说明三者的聚焦结果中主瓣宽度应当基本相同,也即方位向分辨率基本一致.不难看出,阵列1和阵列2的等效阵元都均匀地分布在孔径面上,很好地满足上述第一条均匀性的设计原则.相比而言,阵列3的等效孔径则不满足均匀性,这势必导致其等效阵元在孔径面内的某块区域或沿某些方向产生冗余,使得其等效孔径沿某些方向投影所得的一维等效线阵不满足均匀、周期排列的特点,进而提升这些方向的旁瓣水平,干扰成像结果.再从第二条设计原则的角度来分析.阵列2的等效孔径是一个规则的方形面阵,这导致了该阵列沿0°,45°,135°等角度方向出现明显的阵元遮蔽,因而该面阵结构不满足无明显遮蔽性的原则.而阵列3,十字面阵,它的等效孔径同样在其两个交叉方向(约为45°和135°)上存在一定的遮蔽.反观阵列1,得益于其发射阵列的对称性和接收阵列的随机性,其等效阵元均匀且随机地分布在孔径面上,沿任何方向都不存在明显的遮蔽效应,这也可以说明其等效孔径沿任意方向投影所得的一维线阵都能够很好地满足均匀、周期且单位加权的特点,因而,可以推测该阵列沿任意方向都具有更好的聚焦效果和旁瓣抑制能力.

(a) 阵列1的两组方向图

(b) 阵列2的两组方向图

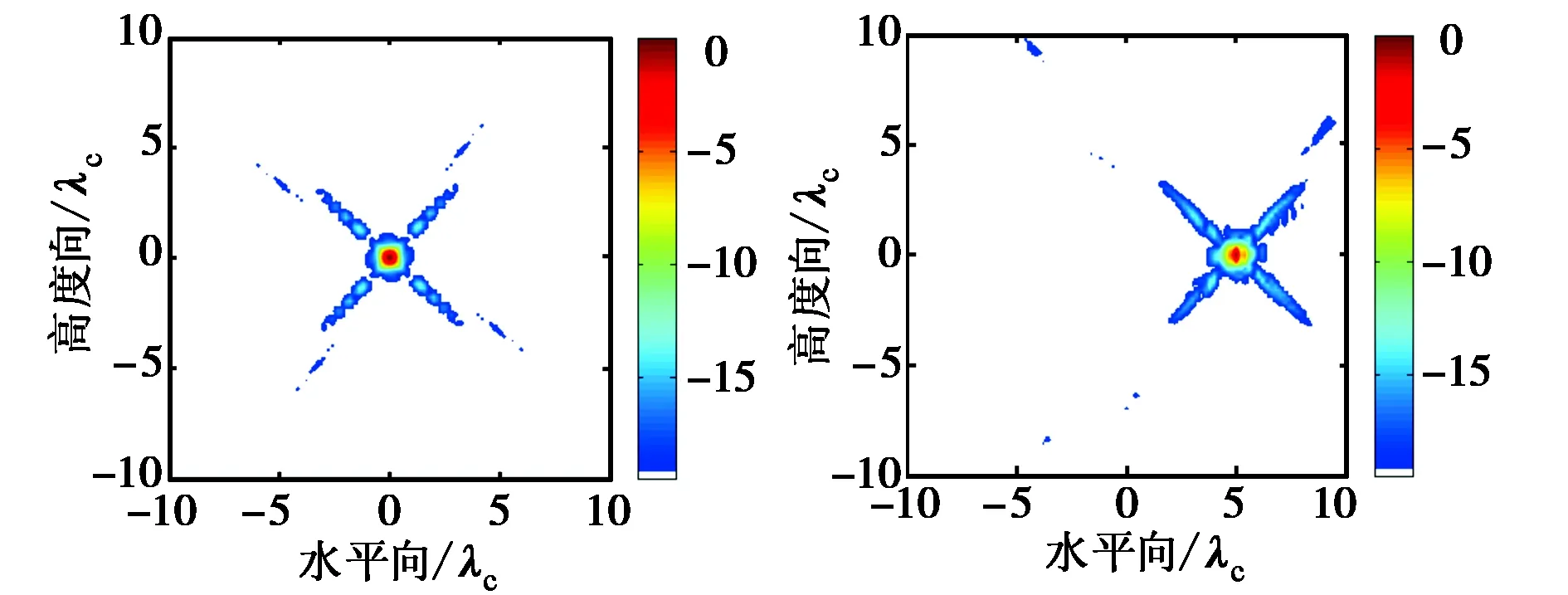
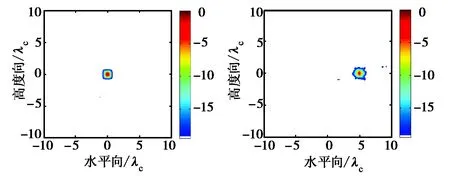
(c) 阵列3的两组方向图图2 仿真获得的三个面阵的方向图(聚焦位置分别在阵列中心正前方(0,0,10λc)处和阵列边缘正前方(5λc,0,10λc)处,显示动态范围均为19.5 dB)

2.2 仿真结果

在本文的仿真中,我们通过如图2所示的近场方向图来分析这三个MIMO面阵的成像性能.仿真中阵列所采用的收发传感器均为赫兹偶极子(Hertzian dipole)单元,发射信号为超宽带窄脉冲,中心频率fc=6 GHz,相对带宽大于100%.图2中的方向图通过如下方式获得:将直径为1 cm的金属小球用作点目标并先后放在阵列中心和边缘正前方10λc(λc=0.05 m对应于中心频率6 GHz)处.散射电磁场通过仿真软件GPR-MAX计算得到,该软件采用有限时域差分法求解波动方程.发射天线依次发射信号,每次发射,所有接收阵元同时接收.然后,利用修正的Kirchhoff徙动算法[12-13]将所有接收回波做相干累加得到三维空间的重建结果.最后,将该三维成像结果沿距离向做最大值投影至水平向和高度向构成的平面上即得到阵列的近场方向图.由于目标距离与阵列尺寸相近,因而图2中的方向图并未采用极坐标的形式表示,而是采用直角坐标的形式给出,且三组方向图均在相同的动态水平19.5 dB下显示.

首先,分析阵列中心位置的聚焦情况,即图2中左侧的三组结果.与本文之前的理论分析一致,阵列3由于其等效孔径非均匀分布,沿其交叉方向存在明显的冗余,导致其主瓣附近的相干区域内受到沿这些方向的旁瓣的严重“污染”,这些“污染”将会直接影响该阵列对空间位置连续的复杂目标成像时的效果.而阵列2,由于其沿多个角度都存在明显遮蔽,因而沿这些角度,成像结果中的非相干区域内都出现了明显的旁瓣.综合来看,由于既满足均匀性又无明显遮蔽,只有阵列1中心位置的聚焦结果在19.5 dB的动态范围下几乎没有出现干扰旁瓣.再对比图2右侧的三组边缘位置聚焦结果.从图中可以看到,三者边缘位置的方向图与中心位置的情况基本类似,只是旁瓣水平都要略高于对应的中心位置的结果.

(a) 阵列1方向图曲线

(b) 阵列2方向图曲线

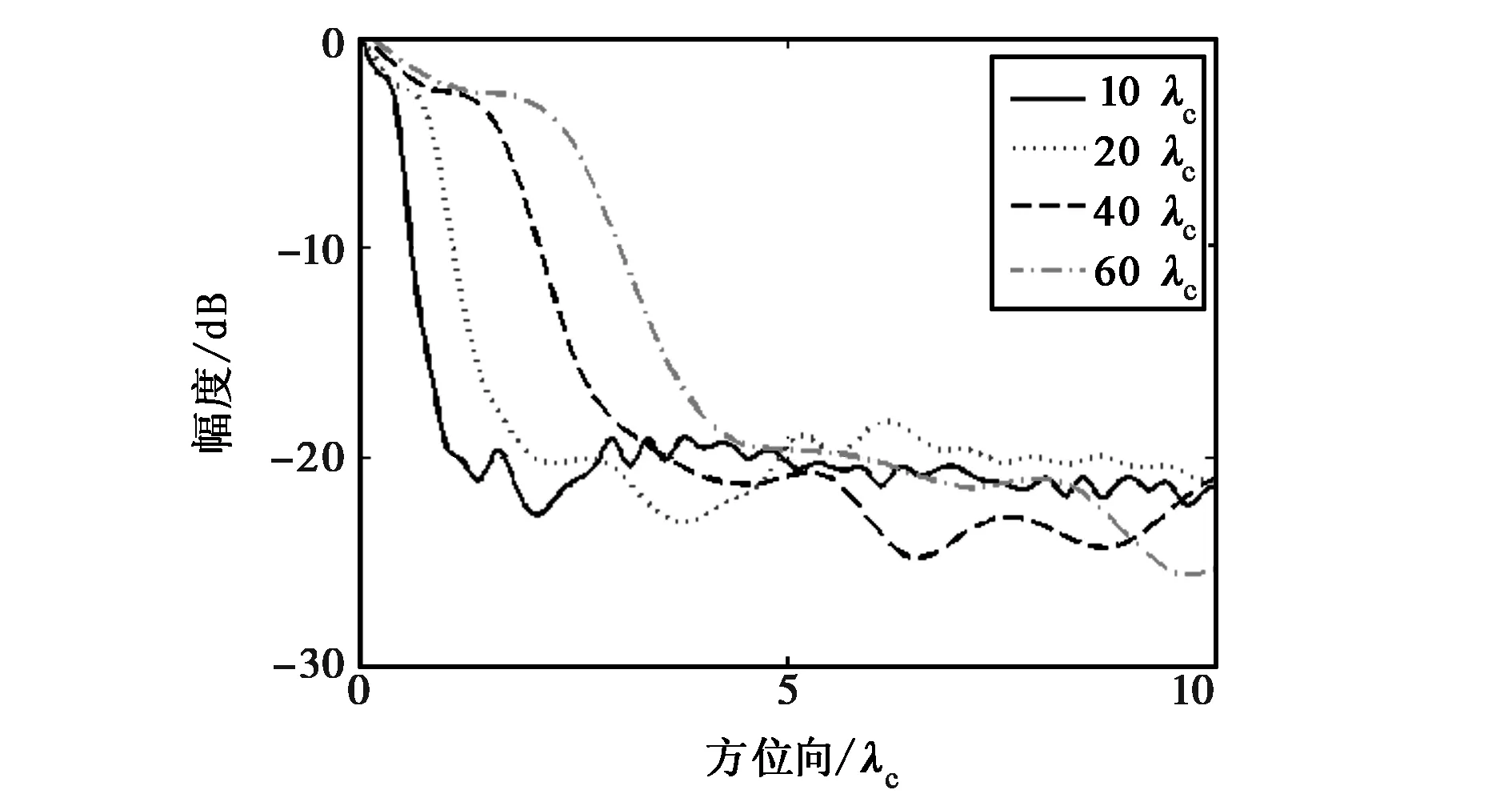
(c) 阵列3方向图曲线图3 三个阵列在不同聚焦距离下的方向图曲线

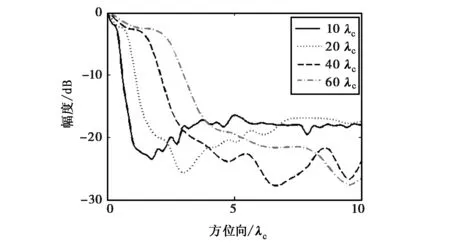
由于阵列的方向图和聚焦的距离有关,因而我们用同样的方法仿真获取了点目标位于阵列中心正前方其他不同距离下的结果,如图3所示.为了方便显示,图3中各组方向图是由类似图2中的最大投影结果,再以目标位置为中心,旋转360°,取方位向沿各个角度最大值所得到的曲线.从三组方向图曲线可以看到,另外三个不同距离下的结果与10λc下的情况基本相同,这也说明了本文提出的阵列结构在不同的聚焦距离下均有良好的表现.这里,不妨定义图3曲线中第一个波谷以内的区域为主瓣所在区域,其他外部区域全部为旁瓣.依此获得了三个面阵在不同距离下的峰值旁瓣水平,列于表1中.可以看到,在四个不同距离下,面阵1的峰值旁瓣水平均要低于另两个阵列2 dB以上.上述仿真结果证明了本文提出的新型面阵结构具有良好的聚焦效果和旁瓣抑制能力.

表1 三个二维面阵在不同聚焦距离下的峰值旁瓣水平

二维面阵10λc20λc40λc60λc阵列1-19.04dB-18.61dB-19.20dB-18.91dB阵列2-16.44dB-16.46dB-17.11dB-16.75dB阵列3-13.02dB-12.14dB-13.22dB-13.61dB

3 实验结果

本文中的实验系统采用的是一套1发16收窄脉冲体制的超宽带雷达设备,发射通道接到一个多端口的开关上以实现4个发射单元依次工作.被测阵列的构造及实验场景如图4所示.三个被测阵列的拓扑结构与图1所示完全相同,阵列的尺寸都限制在0.48 m×0.48 m范围内.所使用的天线单元是一种小型四阵元平面阵列天线[14],它的有效带宽范围为2～11 GHz.在构造阵列时,天线单元被垂直固定在一块金属铜板上,如图4(a)所示,该金属板的作用是为了减小后向散射.为了对比这三个阵列对复杂目标的成像效果,实验中所使用的目标是一个形状如字母“A”的物体,该物体表面包裹了一层铜箔以增强其反射效果,如图4(b)所示.为了减小阵列内部天线单元之间的互耦对接收回波产生的不利影响,目标被放置于阵列中心正前方0.5 m处,略大于阵列的宽度.另外,在进行成像实验之前,我们利用金属板的反射回波测定了该实验系统的中心频率与工作带宽,如图5所示.从图中可以看到,系统所使用的超宽带窄脉冲信号其脉冲宽度约为0.14 ns,-10 dB的工作带宽为2.14～9.04 GHz,因而绝对带宽为6.9 GHz,中心频率为5.59 GHz,即相对带宽超过120%,这样的系统参数对于本文的稀疏阵列成像显然是足够了.三个阵列的空间三维重建结果及它们沿距离向的最大值投影如图6所示.与前述仿真类似,这里所采用的相干成像方法仍为修正的Kirchhoff徙动算法.图6中所有成像结果均在相同的动态水平8.5 dB下显示.

(a) 阵列构造 (b) 实验场景图4 实验中阵列的构造及实验场景

(a) 发射脉冲的时域波形 (b) 发射 脉冲的归一化功 率谱密度图5 实验系统所使用的超宽带窄脉冲及其频谱

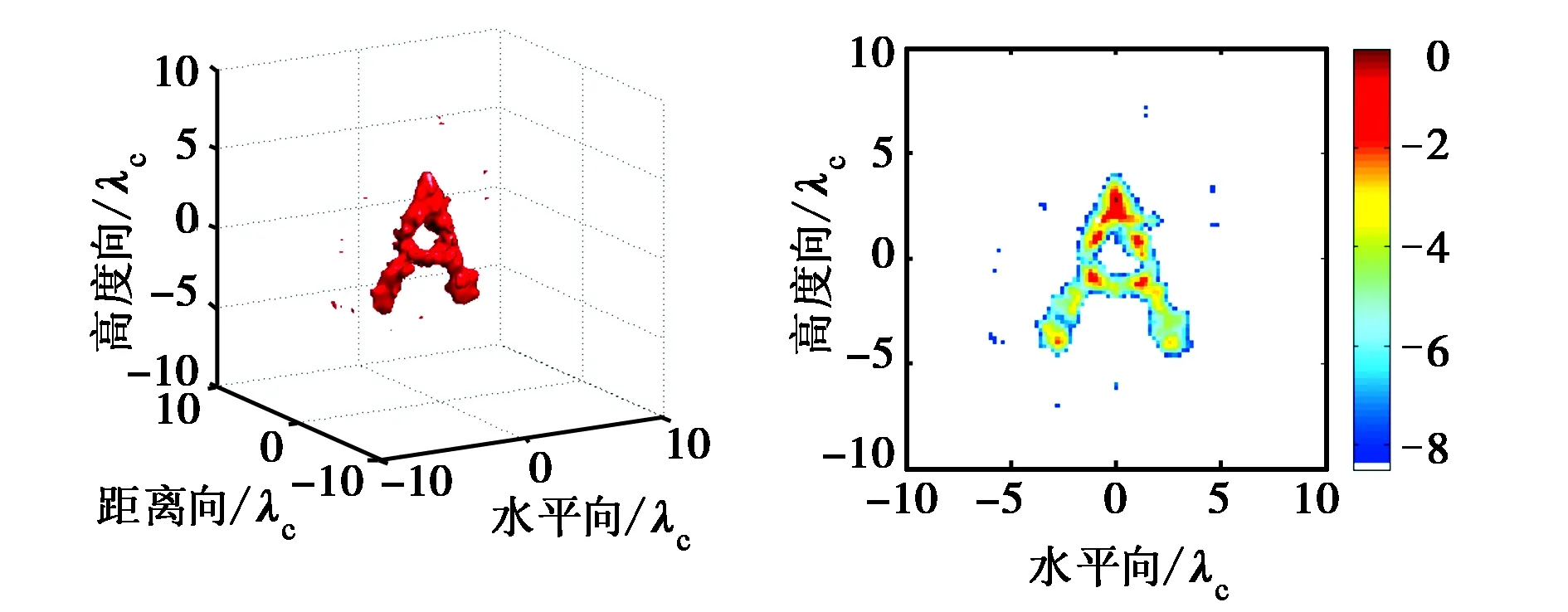
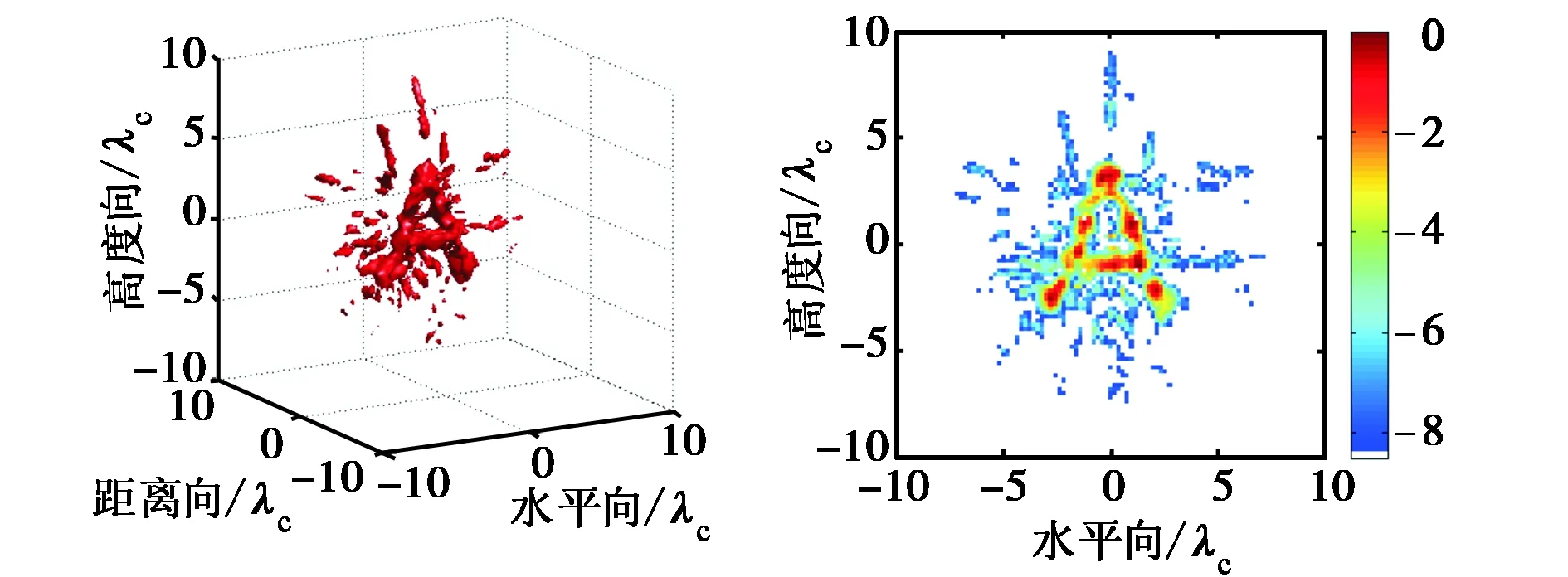
图6的成像结果与前述仿真结果符合得很好.与之前仿真分析的结论类似,阵列3由于不满足等效孔径均匀性的特点,在相干区域内的旁瓣抑制能力较弱,导致相干区域内的旁瓣“污染”了真实目标,聚焦效果不理想,目标未能很好地被重建出来.例如,图6(c)中字母“A”的两条“臂”粗细差别过大,明显与真实目标不符.而对于阵列2,从图6(b)中的投影不难看出,目标的基本形状已被大致重建出来,这得益于该面阵的等效孔径满足均匀分布的特点.然而,在存在明显阵元遮蔽的方向上,该阵列都出现了大量的旁瓣,且这些能量的泄漏严重地干扰了整个成像结果,这显然不是我们想要的.图6(a)中阵列1的成像结果显然与真实目标符合得最好,且未出现明显的旁瓣,字母“A”中每一个部位基本都能够被清晰地显示和辨认.综上,实验结果进一步印证了该新型面阵结构良好的成像性能和旁瓣抑制能力.结合其等效阵元个数较少(4×16=64个)的特点,该新型面阵拓扑结构为高效、实时超宽带近距离高分辨率成像的应用提供了可能.

(a) 阵列1成像结果

(b) 阵列2成像结果

(c) 阵列3成像结果图6 字母“A”的三维空间成像结果及它们沿距离向的最大值投影(目标摆在阵列中心正前方约10λc处,所有结果显示的动态范围均为8.5 dB)

4 结 论

本文分析并总结了二维超宽带MIMO稀疏面阵拓扑结构的两条设计原则:等效孔径的均匀性与无明显遮蔽性.同时,提出了一种符合这两条设计原则的新型MIMO面阵拓扑结构.通过仿真得到的阵列方向图证明了该面阵结构相比其他两个相同尺寸、相同阵元数目的MIMO面阵,具有更好的聚焦效果和旁瓣抑制能力.并且对于不同距离下所获得的聚焦结果,该面阵的峰值旁瓣水平均要低于另两个阵列2 dB以上.对复杂目标三维成像的实验结果进一步印证了该面阵良好的成像性能.因此,结合其等效阵元个数较少的特点,本文提出的这种新型MIMO面阵拓扑结构为高效、实时的超宽带近距离高分辨率成像提供了可能.

[1] SCHWARTZ J L, STEINBERG B D. Ultrasparse, ultrawideband arrays[J]. IEEE transactions on ultrasonics, ferroelectronics, and frequency control, 1998, 45(2): 376-393.

[2] ZHUGE X D, YAROVOY A G. Sparse multiple-input multiple-output arrays for high-resolution near-field ultra-wideband imaging[J]. IET microwaves, antennas and propagation, 2011, 5(13): 1552-1562.

[3] LOCKWOOD G R, FOSTER F S. Optimizing the radiation pattern of sparse periodic two-dimensional arrays[J]. IEEE transactions on ultrasonics, ferroelectronics, and frequency control, 1996, 43(1): 15-19.

[4] 张驰, 李悦丽, 周智敏. 基于独立分量分析法的稀疏阵列穿墙成像雷达直达波干扰抑制[J]. 雷达学报, 2014, 3(5): 524-532.(in Chinese)

ZHANG C, LI Y L, ZHOU Z M. Wall clutter mitigation in through-the-wall imaging radar with sparse array antenna based on independent component analysis[J]. Journal of radars, 2014, 3(5): 524-532.

[5] YANG B, YAROVOY A, AUBRY P, ZHUGE X D. Experimental verification of 2D UWB MIMO antenna array for near-field imaging radar[C]//Proceedings of the 2009 European microwave conference (EuMC 2009), 2009: 97-100.

[6] 周伟, 刘永祥, 黎湘, 等. MIMO-SAR 技术发展概况及应用浅析[J]. 雷达学报, 2014, 3(1): 10-18.

ZHOU W, LIU Y X, LI X, et al. Brief analysis on the development and application of multi-input multi-output systhetic aperture radar[J]. Journal of radars, 2014, 3(1): 10-18.(in Chinese)

[7] 马超, 顾红, 苏卫民, 等. 多输入多输出阵列的机载前视雷达成像算法[J]. 电波科学学报, 2015, 30(1): 21-28.

MA C, GU H, SU W M, et al. Algorithm for airborne forward-looking imaging radar based on multiple input multiple output antenna array[J]. Chinese journal of radio science, 2015, 30(1): 21-28.(in Chinese)

[8] 孟藏珍, 许稼, 花良发, 等. 基于接收滤波器设计的MIMO-SAR波形耦合抑制[J]. 电波科学学报, 2014, 29(3): 401-407+423.

MENG C Z, XU J, HUA L F, et al. MIMO-SAR waveform coulpling suppressing based on design of receiving filter[J]. Chinese journal of radio science, 2014, 29(3): 401-407+423.(in Chinese)

[9] ZHUGE X D, YAROVOY A G. Study on two-dimensional sparse MIMI UWB arrays for high resolution near-field imaging[J]. IEEE transactions on antennas and propagation, 2012, 60(9): 4173-4182.

[10] 董健, 刘芳, 蒋艺, 等. 基于几乎差集的多输入多输出雷达阵列稀疏优化方法[J]. 电波科学学报, 2015, 30(5): 870-877.

DONG J, LIU F, JIANG Y, et al. Optimization method of thining MIMO radar arrays based on almost difference sets[J]. Chinese journal of radio science, 2015, 30(5): 870-877.(in Chinese)

[11] STEINBERG B D. Principles of aperture and array systems design[M]. New York: Wiley, 1976.

[12] ZHUGE X D, YAROVOY A G, SAVELYEV T G, LIGTHART L P. Modified Kirchhoff migration for UWB MIMO array-based radar imaging[J]. IEEE transactions on geoscience and remote sensing, 2010, 48(6): 2692-2703.

[13] 吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展(科普类)[J]. 雷达学报, 2014, 3(4): 383-395.

WU Y R, HONG W, ZHANG B C, et al. Current developments of sparse microwave imaging[J]. Journal of radars, 2014, 3(4): 383-395.(in Chinese)

[14] WANG Y C, SHAO J J, CHEN C, et al. Four-element planar array antenna for UWB application[C]//2014 15th international conference on ground penetrating radar (GPR), 2014: 787-79.

谭恺 (1986-),男,湖南人，博士研究生,研究方向为超宽带雷达信号处理,超宽带MIMO阵列设计、成像及穿墙运动目标检测与跟踪技术.

吴世有 (1985-),男，安徽人，博士,研究方向为超宽带雷达目标检测、成像技术和软件开发.

方广有 (1963-),男，河南人，研究员,博士生导师,主要从事超宽带电磁场理论及其工程应用、超宽带雷达成像技术、微波成像新方法和新技术等方面的研究工作.

Two-dimensional sparse MIMO array topologies for UWB high-resolution imaging

TAN Kai1,2WU Shiyou1WANG Youcheng1,2YE Shengbo1CHEN Jie1FANG Guangyou1

(1.InstituteofElectronics,ChineseAcademyofSciences,Beijing100190,China; 2.UniversityofChineseAcademyofSciences,Beijing100039,China)

In this paper, two principles for designing two-dimensional (2D) multiple-input multiple-output (MIMO) array topology are summarized, which are uniform distribution and less element shadowing for effective aperture. According to these two design principles, a novel 2D MIMO antenna array topology is proposed for UWB short-range high-resolution imaging. Compared with other two different arrays having the same number of transceivers, the proposed array has a better control over the sidelobe level (SL) both in the interference region (IR) and non-interference region (NIR) of the simulated radiation patterns. And for patterns of different focusing distances, the peak sidelobe levels (PSLs) of the proposed array are lower than the compared ones over 2 dB. Experimental imaging results for a distributed target also verify the outstanding imaging capability of the proposed array. Therefore, with a small number of effective elements, the proposed array topology has potential applications for high-efficiency ultra-wideband short-range imaging.

ultra-wideband radar; high-resolution imaging; multiple input multiple output array; two-dimensional array topology

10.13443/j.cjors.2015121701

2015-12-17

国家科技支撑计划(2014BAK12B03); 国家863计划(2012AA121901); 国家自然科学青年基金(61501424); 北京市交通委员会科技支撑项目(TC1405473)

TN955

A

1005-0388(2016)04-0779-07

谭恺, 吴世有， 王友成， 等. 用于超宽带高分辨率成像的二维稀疏MIMO面阵拓扑结构研究[J]. 电波科学学报,2016,31(4):779-785.

TAN K, WU S Y， WANG Y C， et al. Two-dimensional sparse MIMO array topologies for UWB high-resolution imaging[J]. Chinese journal of radio science,2016,31(4):779-785. (in Chinese). DOI: 10.13443/j.cjors.2015121701

联系人： 谭恺 E-mail：tankai@yeah.net