电大均匀介质目标三维散射的并行多层快速多极子计算
邸瀚漪 杨明林 盛新庆
(北京理工大学信息与电子学院电磁仿真中心,北京 100081)
电大均匀介质目标三维散射的并行多层快速多极子计算
邸瀚漪 杨明林 盛新庆
(北京理工大学信息与电子学院电磁仿真中心,北京 100081)
实现了计算电大均匀介质体散射问题的高效混合并行混合场积分方程(Electric and Magnetic Current Combined-Field Integral Equation,JMCFIE)求解,在单纯消息传递接口(Message Passing Interface,MPI)并行基础上采用共享存储并行编程(Open Multi-Processing,OpenMP)进一步提升性能.该混合MPI与OpenMP的并行多层快速多极子技术通过灵活的进程和线程策略,提升了负载平衡和可扩展性.数值实验展示了此混合MPI与OpenMP的并行多层快速多极子技术的计算能力,计算了不同尺寸的电大目标体(包含一个半径120 m、1.1亿未知数目的介质球).
JMCFIE方程;多层快速多极子;混合并行技术
DOI 10.13443/j.cjors.2015110601
引 言
积分方程法是计算电磁学中的一种高效、精确算法,广泛应用于均匀介质体的电磁散射计算[1-4],在许多实际应用中,例如卫星介质组件设计、飞机座舱盖以及光学组件的设计方面有很多重要应用.积分方程根据不同边界条件的组合、试函数选取的不同,以及方程之间配比的不同,可以获得具有不同性态与精度的方程形式[5-7].通常说来,这些方程可以分为切向或者法向方程,或者是两者的不同组合形式.在不同的方程中,被人们广泛使用的有联合切向方程(Combined Tangential Formulation,CTF)和混合场积分方程(Electric and Magnetic Current Combined-Field Integral Equation,JMCFIE)[5].JMCFIE作为CTF与联合法向方程 (Combined Normal Formulation,CNF)的组合形式,既具有较高的计算精度,同时矩阵性态相比CTF获得很大改善,因此比较适用于电大尺寸目标体的计算.
积分方程最终离散成为一个大规模的矩阵方程,可以采用迭代法求解,如广义最小残差法(Generalized Minimal Residual Method,GMRES)求解.矩阵矢量相乘可采取不同的加速算法.在这些算法中,多层快速多极子算法(Multi-Level Fast Multipole Algorithm,MLFMA)发展较为成熟,可以被用来解决一些具有挑战性的问题[6].然而,对于未知量超过千万的电大尺寸问题,单一进程串行运算的MLFMA已经远远无法满足计算需求.
为了解决这类电特大问题,各类基于大规模并行分布式内存计算平台开发的多层快速多极子技术被相继提出,在过去的十几年里,对金属体散射问题的仿真分析通过采用不同的并行方案,计算能力由千万未知数升到十亿未知数[7-9].近来,基于消息传递接口(Message Passing Interface,MPI)并行的并行多层快速多极子技术,实现了对不同材料参数下均匀介质体电大目标的计算.然而,由于各个进程间过度的消息交换、负载的不均衡以及数据的复制传递等原因,单纯的基于MPI的并行方案常常表现得效率低下.
本文提出了一种灵活而高效的混合MPI和共享存储并行编程(Open Multi-Processing, OpenMP)的并行多层快速多极子技术(MPI-OpenMP-MLFMA)应用到计算均匀介质体散射问题的JMCFIE方程求解中,实现对电大均匀介质体散射问题的快速求解.此混合并行对于MLFMA树结构的并行采用低层按盒子并行以及高层按平面波并行的混合划分策略.MLFMA树结构按照上述并行策略被划分到每一个处理器进程中,构建一个基于MPI的并行;之后,每一个处理器进程又被进一步地按照OpenMP进行了并行化,构建了多线程的并行[10].此种多层快速多极子的混合并行对于计算大尺寸问题具有很强的计算能力.
1 JMCFIE方程
对于一个给定的均匀介质体,对内部和外部各自依据等效原理,可以获得一系列的关于等效电磁流的积分方程来计算电场磁场[7]:介质体外部的电场积分方程(Electric Field Integral Equation Outside,EFIE-O),介质体外部的磁场积分方程(Magnetic Field Integral Equation Outside,MFIE-O),介质体内部的电场积分方程(Electric Field Integral Equation Inside,EFIE-I),以及介质体内部的磁场积分方程(Magnetic Field Integral Equation Inside,MFIE-I)分别为:
E1-η1L1(J1)+K1(M1)=Ei(EFIE-O),
(1)

(2)
E2-η2L2(J2)+K2(M2)=0 (EFIE-I),
(3)
(4)
式中: ηl(l=1,2)分别表示介质体外与介质体内的均匀空间波阻抗; 算子L和算子K定义为

(5)
Kl{X}(r)=∫SX(r′)×′Gl(r,r′)dr′,
(6)
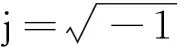
不同的等效方程的组合,不同的试函数的选取,不同的方程配比比例,都会产生出各种不同的求解面等效问题的积分方程,如PMCHW方程(Poggio-
Miller-Chang-Harrington-Wu Formulation,PMCHW),CTF方程,CNF方程以及JMCFIE方程.JMCFIE方程是由CTF方程和CNF方程的线性组合而成的,就如在计算金属物体散射问题的CFIE方程一样,在精度和效率之间获得了很好的平衡[5].JMCFIE方程可以表示为
二十世纪八十年代初,《胭脂扣》一经出版便在文坛上引起巨大轰动,尤其在1987年被搬上荧屏后,在一系列商业性的运作下李碧华的创作得到各方关注,其本人也成了香港炙手可热的女作家。王德威先生曾对李碧华的创作有过一段精当的点评:“想象穿梭于古今生死之间,探勘情欲轮回,冤孽消长,每每有扣人心弦之处,而她的故事今判的笔法,也间接写出香江风月的香貌。”李碧华的作品绝非简单的言情叙事,它始终具有浓郁的传统色彩及香港印记。
(7)



(8)
2 混合并行多层快速多极子技术
当应用MLFMA时,开始矩阵的近相互作用被计算并显式储存.矩阵的远相互作用的计算分组进行,计算过程包括聚集、转移、发散三个部分[7].对于无损耗均匀介质而言,其波数k是一个常数,通过利用聚集和发散矩阵的对称性,可以将聚集和发散矩阵的内存需求减少一半,转移矩阵的内存需求可以减少到原来的四分之一.然而,对于有耗均匀介质情况,波数k成为复数,含有虚部,此时MLFMA将失去其对称性,但我们依然可以利用中心移置矩阵的对称性:
(9)
同时,我们使用了下三角近似Schur补预处理技术(Lower Triangular Approximate Schur Preconditioner,LTASP),以减少构造预处理矩阵的复杂度.通过忽略子分块矩阵间极小的耦合矩阵Z12,最有用的近相互作用的信息被保存下来.然后对预处理矩阵求逆,得到
(10)
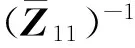
在未知数目大于千万的电大尺寸的计算中,为了提高JMCFIE方程的求解能力,可以采用高效的并行计算技术实现快速仿真.对于MLFMA而言,采用混合的或者是叠加的划分策略,且此两种策略已经被成功应用于未知数过亿目标的仿真分析.然而,这两种策略都有其局限.最近,一种混合实现的并行策略在文献[10]中被提出,且被证实灵活且高效,可以实现未知数目超过10亿的目标的仿真分析.此混合并行可以使得传输层转向较细层来提高计算效率因而具有较好的数值扩展性.在此,我们不对具体的过程进行详细介绍,详细过程读者可参考文献[10].
3 数值结果与讨论
为了研究上述讨论算法的计算精度、效率和计算能力,在这一部分我们将会展示一系列的数值实验.所有的计算都是在北京理工大学信息与电子学院电磁仿真中心Liuhui II高性能并行计算平台上进行的.它有10个节点,每个节点2个Intel X5650 2.66 GHz CPU共12个核,96 Gb内存.迭代求解器为GMRES,迭代残差0.001,重启动数100.定义散射角0°与180°分别为后向与前向.
首先,研究的是该并行算法的并行效率.我们主要针对的是固定目标,随着计算单元数的增加,本文提出算法的并行效率与传统基于MPI的并行算法的差别.计算目标为直径60 m的球体,入射波频率0.3 GHz.对于此球体,其材料的相对介电常数为2.采用三角形离散后,共产生2 880 000 三角形单元,4 300 000 条边,总的未知量为8 600 000.图1 展示了在每个进程采用两个线程时纯MPI并行,并行效率随计算单元数的变化情况.在此我们选择8个进程时纯MPI的并行效率为1.从图1可以看出,在32个计算单元时,本文提出的算法并行效率仍然在80%以上.
接下来,为了展示本文提出的MPI-OpenMP-MLFMA混合并行多层快速多极子技术的强大计算能力,我们计算了两个电特大尺寸介质球体.其中一个是半径100 m,相对介电常数为εr=2-j的有耗球体;另一个为半径120 m,相对介电常数为2的均匀无耗介质球体.详细的计算资源统计如表1所示,计算的雷达散射截面积(Radar Cross-Section, RCS)结果与Mie解的比较如图2和图3所示.特别的,列出了范围在174°~180°的RCS结果.从中我们可以看出,计算结果吻合得很好.当目标为有吸收的情况下,迭代求解比无吸收收敛步数少,计算时间短.

图1 并行效率随计算单元数变化情况

参数算例1算例2半径/m100120相对介电常数2-0.1j2未知数目96000000111974400计算单元数100126迭代步数44383内存/Gb890784计算时间/h3.225

图2 半径为100 m有耗介质球、相对介电常数为2-0.1j双站VV极化RCS计算结果
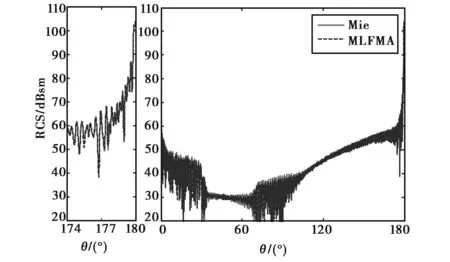
图3 半径为120 m的无耗介质球、相对介电常数为2双站VV极化RCS计算结果
4 结 论
本文提出了一种基于JMCFIE方程计算大尺寸均匀目标体的散射问题的混合并行多层快速多极子算法.该并行算法通过采用MPI和OpenMP混合并行进一步提升了负载均衡以及数据的可扩展性.为了减少内存需求,在无耗和有耗材料中分别应用了MLFMA的对称性.对半径为100 m和120 m,模拟未知数过亿的电大均匀介质球的散射问题计算展示了该并行策略良好的数据可扩展性和强大的计算能力.
[1] SHENG X Q, JIN J M, SONG J, et al. Solution of combined-field integral equation using multilevel fast multipole algorithm for scattering by homogeneous bodies[J]. IEEE transactions on antennas and propagation, 1998, 46(11): 1718-1726.
[2] 阙肖峰, 聂在平, 胡俊. 三维导体介质复合结构电磁辐射与散射的MLFMA分析[J]. 电波科学学报, 2007, 22(6):893-898.
QUE X F, NIE Z P, HU J. Analysis of EM radiation and scattering properties for 3-D combined conducting and dielectric objects by using MLFMA[J]. Chinese journal of radio science, 2007, 22(6): 893-898. (in Chinese)
[3] 伍月千, 盛新庆. 均匀介质目标高阶矩量法的高效预处理方法[J]. 电波科学学报, 2012, 27(6): 1099-1104.
WU Y Q, SHENG X Q. Efficient precondition algorithm for higher order method of moments for homogeneous dielectric objects[J]. Chinese journal of radio science, 2012, 27(6): 1099-1104. (in Chinese)
[4] 丁振宇, 洪伟. 快速多极子在任意截面均匀介质柱散射中的应用[J]. 电波科学学报, 2001, 16(3):283-286.
DING Z Y, HONG W. Application of FMM to electromagnetic scattering from a homogeneous cylinder of arbitraty cross section[J]. Chinese journal of radio science, 2001, 16(3): 283-286. (in Chinese)
[5] ERGÜL Ö, GÜREL L. Comparison of integral-equation formulations for the fast and accurate solution of scattering problems involving dielectric objects with the multilevel fast multipole algorithm[J]. IEEE transactions on and propagation, 2009, 57(1): 176-187.
[6] SONG J M, LU C C, CHEW W C. Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects[J]. IEEE transactions on and propagation, 1997, 45(10): 1488-1493.
[7] VELAMPARAMBIL S, CHEW W C, SONG J M. 10 million unknowns: is it that big?[J]. IEEE antennas and propagation magzine, 2003, 45(2): 43-58.
[8] GÜREL L, ERGÜL Ö . Fast and accurate solutions of extremely large integral-equation formulations discretised with tens of millions of unknowns[J]. Electron letter, 2007, 43(9): 499-500.
[9] PAN X M, SHENG X Q. A sophisticated parallel MLFMA for scattering by extremely large targets[J]. IEEE antennas and magzine, 2008, 50(3): 129-138.
[10]PAN X M, PI W C, YANG M L, et al. Solving problems with over one billion unknowns by the MLFMA[J]. IEEE transactions on antennas and propagation, 2012, 60(5): 2571-2574.

邸瀚漪 (1990-),男,山西人,北京理工大学信息与电子学院研究生,研究方向为计算电磁算法.

杨明林 (1984-),男,山东人,北京理工大学讲师,研究方向为计算电磁学高效算法及算法并行化实现.

盛新庆 (1968-),男,安徽人,北京理工大学教授,研究方向为计算电磁学、目标电磁特性、微波成像及遥感、天线理论及设计.
An efficient parallel approach of MLFMA for solving 3D scattering by large homogeneous targets
DI Hanyi YANG Minglin SHENG Xinqing
(CenterforElectromagneticSimulation,SchoolofInformationandElectronics,BeijingInstituteofTechnology,Beijing100081,China)
Based on the electric and magnetic current combined-field integral equation (JMCFIE), a fast algorithm is presented for calculating 3D scattering by large homogeneous objects. An efficient and flexible parallel implementation of the multilevel fast multipole algorithm (MLFMA) is employed to enhance efficiency and capability of the JMCFIE approach. This parallel approach is proposed by using open multi-processing(OpenMP) to further accelerate the pure MPI parallel MLFMA. This hybrid MPI-OpenMP paralleled MLFMA improves the load-balance and scalability by combing processes and threads flexibly, hence depress unavoidable load imbalance in the pure MPI parallel MLFMA. Numerical experiments on targets with different sizes including a dielectric sphere with radius 120 m modeled with about 110 million unknowns show the scalability and computational capability of the proposed MPI-OpenMP-MLFMA enhanced JMCFIE for extremely large targets.
JMCFIE; MLFMA; hybrid MPI and OpenMP parallization
10.13443/j.cjors.2015110601
2015-11-06
国家自然科学基金(61371002); 111引智计划(B14010)
O441.4
A
1005-0388(2016)04-0695-05
邸瀚漪, 杨明林, 盛新庆. 电大均匀介质目标三维散射的并行多层快速多极子计算[J]. 电波科学学报,2016,31(4):695-700.
DI H Y, YANG M G, SHENG X Q. An efficient parallel approach of MLFMA for solving 3D scattering by large homogeneous targets[J]. Chinese journal of radio science,2016,31(4):695-700.(in Chinese). DOI: 10.13443/j.cjors.2015110601
联系人: 杨明林 E-mail: yangminglin@bit.edu.cn

