电离层加热中朗缪尔湍动的数值模拟研究

刘默然 周晨 赵正予 张援农

(武汉大学电子信息学院,武汉 430072)



电离层加热中朗缪尔湍动的数值模拟研究

刘默然 周晨 赵正予 张援农

(武汉大学电子信息学院,武汉 430072)

应用广义Zakharov模型,“全尺度”模拟了大功率电波垂直注入电离层后电磁波与电离层的非线性相互作用.在寻常波(O波)反射点附近,无线电波参量衰减为电子等离子体波和离子声波两种波模,接着,伴随着坍塌、空洞形成以及强烈电子等离子体波的俘获相关过程,形成的空洞会导致慢非寻常波(Z波)的有效激发并能向密度更高的电离层区域传播.模拟结果表明:在毫秒量级的时间尺度内,大功率高频电波在电离层等离子体中的O波反射点附近激发出了电子朗缪尔波和离子声波,同时波粒相互作用导致O波向Z波的转换并传播向更高区域.此研究有助于对参量衰减不稳定性的物理机制形成较直观的印象,对理解大功率高频电波与电离层等的非线性相互作用也很有益处.

加热电离层;参量不稳定性;朗缪尔波;离子声波

DOI 10.13443/j.cjors.2015110602

引 言

虽然欧姆加热理论在高频电波加热电离层研究的初期可以用来解释观测到的众多现象,比如电子温度的升高、电子密度的增加、气辉的增强等等,但随着试验和理论研究的深入,人们发现仅仅欧姆加热机制并不能很好地解释越来越多的加热效果,比如人工扩展F层、场向等离子体不均匀体、受激电磁辐射、等离子体谱线的增强等等.在此基础上,参量不稳定性理论得以提出,并逐渐发展完善.和欧姆加热理论主要用来解释高频电波加热电离层的一级时空效应相对应[1-3],参量不稳定性理论主要用于解释高频电波加热电离层的二级时空效应[4-8].

在加热源和超高频非相干散射雷达垂直入射或沿六个南向的角度入射的实验中,Isham等观测到不寻常的宽度约100 kHz的大幅度的谱线和相对于加热频率上下均为100～300 kHz的平均频移.这个特点被命名为高频加热导致的多普勒频移(HF-induced outshifted line,HFOL).HFOL的谱来自于反射高度之上的3～6 km.有人认为如果反射区域上方为Z波的反射区域的话,HFOL可以解释为来自于O波经过线性转换后的Z波.其过程包括大尺度的密度损耗、Z波的参量衰减和低混杂波的参量衰减[14],以及静电波扰动带来的超热电子的产生,这些过程依次激发电子损耗内部的朗缪尔波,产生了HFOL特点.有关电磁泵波和静电波扰动的相互作用,已经在很多文献中涉及到.本文模拟主要利用Zakharov模型,对大功率电波加热电离层时O波反射区域及O波以上的Z波区域的参量不稳定性过程进行数值模拟及分析.

1 数学模型

1.1 基本方程组

建立电波加热电离层一维数值模型,假设大幅度的电磁波垂直注入垂直分层的电离层,设垂直向上为z轴.在模拟参量不稳定性之前,需要有一个完整的无线电波传播的计算模型,该模型不仅要给出电波能量的分布,还要求给出电场的极化偏振状态.根据Maxwell方程组,引进电动位势矢量A⊥,其满足

(1)

(2)

(3)

式中: c为真空中光速; ε0为真空中介电常数; E表示电场， v表示速度； 下标e表示电子， z表示沿z方向，⊥表示垂直于z方向的平面内.

由于发生参量衰减不稳定性时,电磁波和电子朗缪尔波是高频波模,而离子声波扰动是低频波模,因而需要将方程组中高频量和低频量分离出来进行处理.根据广义Zakharov处理方法,可将方程组中的物理量表示成一个高频分量和一个低频分量之和,即ψ=ψh+ψs.设电离层等离子背景数密度为n0,且离子在高频运动部分是静止不动的,即nih=0以及vih=0,则有ne=n0+nes+neh,ni=n0+nis,ve=veh+ves,vi=vis.低频运动部分采取准中性的等离子体近似处理,认为ves≈vis,nes≈nis(记为ns).低频运动与离子声波扰动相关,这样低频运动速度只有z分量.

基于以上条件及假设,由于电场在水平方向上只有电磁波的高频横向电场,故式(2)、(3)变为

(4)

对于高频分量,电子运动方程和连续性方程如下:

(5)

对于低频分量,电子运动方程和连续性方程如下:

(6)

式(5)、(6)均来自电子和离子的流体动力学方程组,值得注意的是,在将电子的低频量和高频量分离的过程中,非线性项已经约化到电子的低频运动中,而离子的非线性项影响不显著,因而忽略不计.

式(4)、(5)、(6)构成了大功率高频无线电波与电离层等离子体非线性耦合相互作用的出发方程组,也是此研究中数学模型基础.

1.2 数值模型

本文建立的数值模型,是沿z轴(垂直向上为正)的一维模型,高度范围为200～340 km.考虑到参量不稳定性一般发生在反射区域,因此,本文除了E⊥和A⊥需要在200～340 km全范围内以2 m的步进计算外,其余物理量Ezh、neh、nes、veh、vsz均在O波反射区域和Z波反射区域以步进4 cm计算,以求解因静电波扰动带来的小尺度的结构.

1.3 相关物理参数

数值模拟中,有关电离层背景模型,此处考虑一个沿垂直方向分层的等离子体数密度剖面:

n0(z)=nmaxexp[-(z-zmax)2/L2].

(7)

式中: nmax=5×1011m-3表示电离层F2区的密度峰值; zmax=300 km表示F2峰所在的高度; L=31.623 km表示F2峰处电离层特征尺度.离子成分主要是氧离子O+,地磁场B0选择为典型北半球高纬度地区的情形:

(8)

式中: B0=5.0×10-5T; θ=12.41°.

本文的坐标系为:垂直向上为z轴正方向,水平正北为x轴正方向,水平向西为y轴正方向.由所给参数,计算值F2层最大截止频率为fpmax≈6.35 MHz.

选取加热电磁波频率为f0=5.8 MHz,由A-H公式计算可得O波反射高度约为286.614 km.在200 km边界处,给定一个场强为1 V/m的正弦电场E0,电场设为沿着x方向线性极化.计算上边界选在刚刚超过电离层F2峰的340 km处.

2 模拟结果

2.1 无线电波传播模拟结果

数值模型的计算是从200 km处开始的,加热电波从地面传播到下边界大约需要0.67 ms的时间,故实际上数值模拟是从加热开始一段时间后开始进行的.由Maxwell方程组推得的一维电波传播方程的计算结果如图1所示.

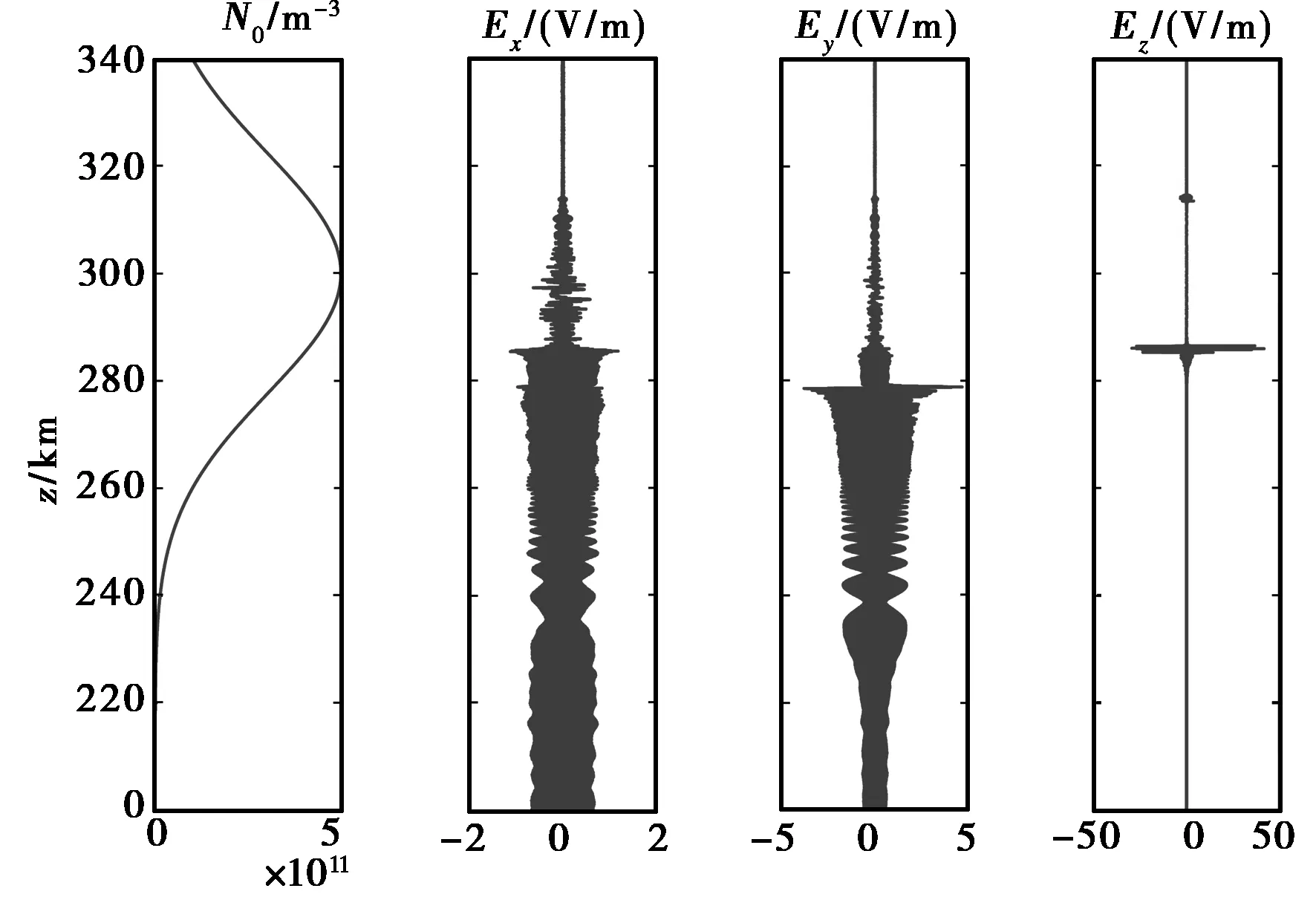
图1 5.8 MHz无线电波电场各分量随高度的分布

初始值在下边界是一个沿着x方向线性极化的波,但是从图1可以看出,在无线电波自下而上的传播过程中,出现了y方向的分量,这是由于法拉利旋转引起的.可以看到,在大约286 km附近有一明显的截止特征,这是O波的反射点,与之前A-H公式计算所得反射高度相符.O波反射点附近出现了明显的z向电场分量,这是由于O波在接近反射点过程中,将逐渐从左旋圆极化变为沿地磁场方向的线性极化.在O波以下区域存在另一个截止特征的区域,则是X波的反射高度,在O波以上,依然有波的存在,但是波的幅度较小,这是部分O波线性模式转换的结果,参量不稳定性导致的电子密度的扰动促使部分O波转换为Z波,向更高处传播.

2.2 O波反射区域与Z波反射区域的参量不稳定性模拟结果

图2是一张整体范围内水平方向的电场随时间变化的图.由图2看出在大约2 ms左右,有参量不稳定性引起的静电波扰动导致O波转换为Z波.

图2 初始电离层电子密度与水平方向电场随时间的变化

图3与图4所示分别为O波反射区域(284～287 km)和Z波反射区(312.5～315.5 km)的Z向电场分布.其中,在大约1 ms之后到达O波反射区域,并形成驻波,而在1.8 ms左右,驻波形式逐渐演化成小尺度大幅度的波.而Z波反射区域在大约2 ms后到达,这与图2的结果相符,之后,可以看到在313.5 km的地方产生幅度较大的波,因为这里是转换点区域[15],即Z波转换为静电波.可以看到,无论是O波反射点还是Z波反射点,都由于参量不稳定性过程产生了比较强的静电波.而由此过程带来的等离子体的扰动如图5所示.

图3 参量不稳定性引起的O波反射区域的静电扰动

图4 参量不稳定性引起的Z波转换区域的静电波扰动

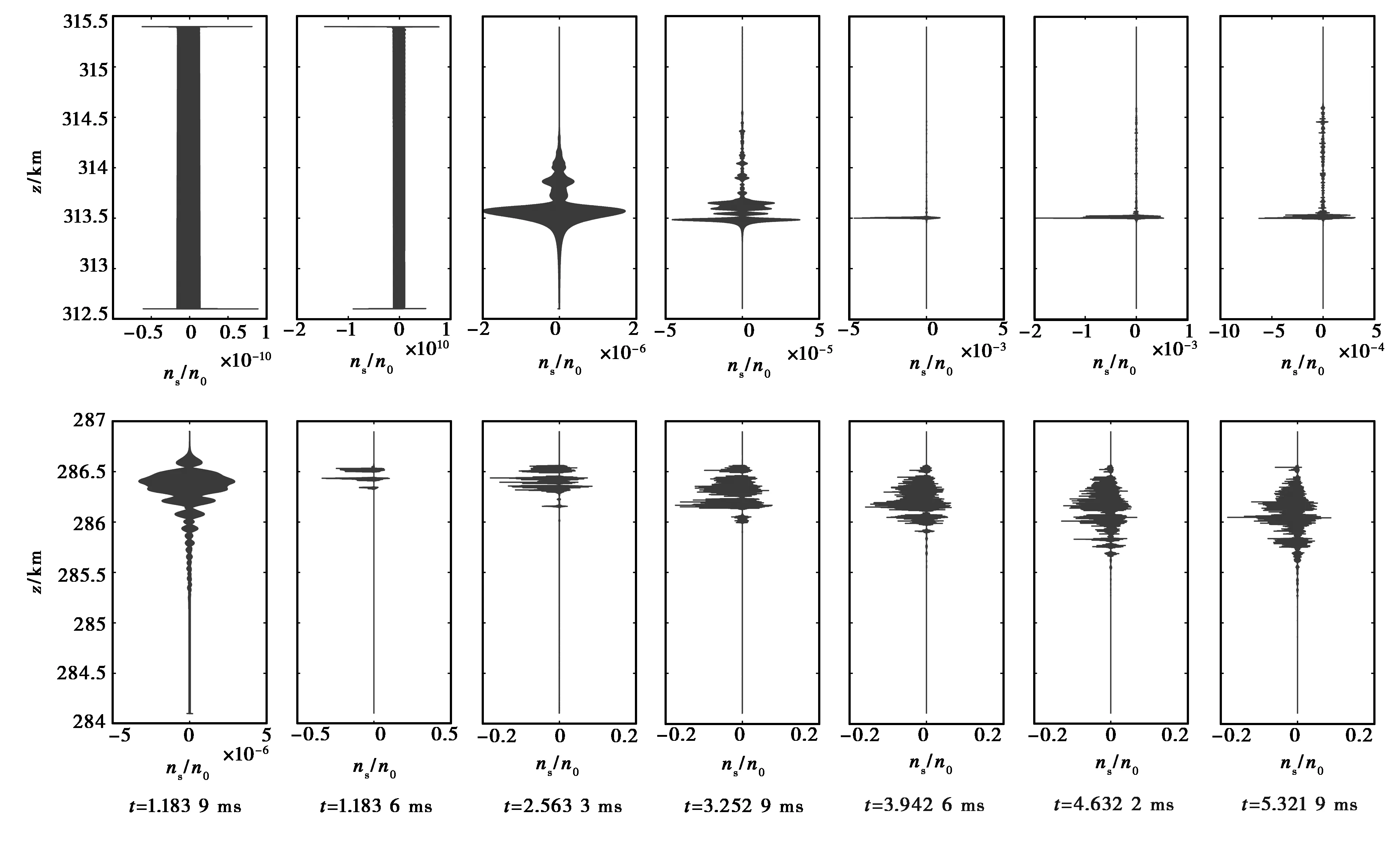
图5 O波反射区域和Z波反射区域内参量不稳定性激发的等离子体密度扰动

如图5所示,O波反射区域在加热1.183 9 ms的时候有电子的扰动,但是很小.在加热1.873 6 ms的时候,电子扰动已经非常明显,这对应的正是图3中驻波演化成的小尺度大幅度的波,即在z=286.4 km和z=286.6 km处电场强度最大的高度,产生了大的扰动.随着时间的推移,这种扰动逐渐地向低处传播.在Z波反射区域,在加热3.942 6 ms的时候电子的扰动变得明显,而且也是在313.5 km处,高度范围非常窄,这对应的是Z波经过参量衰减不稳定性激发出短波段的朗缪尔波和离子声波,随后就是朗缪尔波的崩塌和离子空穴的形成.激发的朗缪尔波有可能转换为O波向上传播出电离层,正如图2所示,在Z波上方依然有部分波向上传播.

朗缪尔波和离子声波的空间尺度均在几十厘米至1 m的量级,因此在相关区域选取4 cm的步进足够模拟出朗缪尔波和离子声波的结果.

3 结 论

本文建立了一维数值模型,模拟了大功率加热电离层情况下,当加热频率略小于F2层最大临界频率时,O波和Z波反射区域的参量不稳定性.结果表明:加热电磁波在O波反射区域发生了参量性衰减,O波的衰减激发了朗缪尔波和离子声波的形成,相对于O波的百米量级的波长,激发的两种波模只有米量级甚至更短的波长.这种不稳定性之后是快速的朗缪尔波的崩塌和离子空穴的形成,以及通过朗缪尔扰动带来的大幅度的波模转换,形成了Z波模式.Z波向上传播,穿越F2层层顶,并到达其转换点,转换为静电波.在顶层,Z波经过参量不稳定性,衰减为小尺度(大约几十厘米)的耦合静电波和离子声波,随之而来的又是朗缪尔波的崩塌和离子空穴的形成.最后,Z波衰减的朗缪尔波又生成O波,传播出电离层.以上过程均发生在毫秒量级.

[1] 倪彬彬, 赵正予, 项薇, 等. 高频泵波加热电离层的数值模拟[J]. 电波科学学报, 2004, 19(3): 274-279.

NI B B, ZHAO Z Y, XIANG W, et al. Numerical modeling of ionospheric modification with powerful HF pump waves[J]. Journal of radio science, 2004, 19(3): 274-279. (in Chinese)

[2] 黄文耿, 古士芬, 龚建村. 大功率高频无线电波加热电离层[J]. 电波科学学报, 2004, 19(3): 296-301.

HUANG W G, GU S F, GONG J C. Ionospheric heating by powerful high-frequency radio waves[J]. Journal of radio science, 2004, 19(3): 296-301. (in Chinese)

[3] 何昉, 赵正予, 倪彬彬, 等. 不同加热条件下加热电离层的效应研究[J]. 电波科学学报, 2006, 21(4): 525-531.

HE F, ZHAO Z Y, NI B B, et al. Study on the ionospheric effects with different heat-conditions[J]. Journal of radio science,2006, 21(4): 525-531. (in Chinese)

[4] ARNUSH D, FRIED B D, KENNEL C F. Parametric amplification of propagating electron plasma waves in the ionosphere[J]. Journal of geophysics research, 1974, 79(13): 1885-1993.

[5] CARLSON H C, DUNCAN L M. HF excited instabilities in space plasmas[J]. Radio science, 1977, 12(6): 1001-1013.

[6] CRAGIN B L, FEJER J A, LEER E. Generation of artificial spread-F by a collisionally coupled purely growing parametric instability[J]. Radio science, 1977, 12(2): 273-284.

[7] WEINSTOCK J, BEZZERIDES B. Nonlinear saturation of parametric instability: spectrum instabilities[J]. Physics of fluids, 1973, 16(12),2287-2303.

[8] WONG A Y, TAYLOR R J. Parametric excitation in the ionosphere[J]. Physics review letters, 1971, 19(3): 274-279.

[9] GANGULY S, GORDON W E. Heater enhanced topside plasma line[J]. Geophysics ressearch letters, 1983, 10(10): 977-978.

[10]RIETVELD M T, ISHAMM B, GRTDELAND T, et al. HF-pump-induced parametric instabilities in the auroral E-region[J]. Advances in space research, 2002, 29(9): 1363-1368.

[11]MISHIN E, HAGFORS T, KOFMAN W. On origin of outshifted plasma lines during HF modification experiments[J]. Journal of geophysics research space physics, 1997, 102(A12): 27265-27269.

[12]GONDARENKO N A, GUZDAR P N, OSSAKOW S L, et al. Linear mode conversion in inhomogeneous magnetized plasmas during ionospheric modification by HF radio waves[J]. Journal of geophysics research, 2003, 108(A12): 553-559.

[13]GONDARENKO N A, OSSAKOW S L, MILIKH G M. Nonlinear evolution of thermal self-focusing instability in ionospheric modification at high latitudes: aspect angle dependence[J]. Geophysics research letters, 2006, 33(16): 399-423.

[14]KUO S P, KORETZKY E, LEE M C. Parametric excitation of lower hybrid waves by Z-mode waves near electron cyclotron harmonics at Tromso[J]. Journal of geophysical research, 1998, 103(103): 23373-23379.

[15]MISHIN E, HAGFORS T, ISHAM B. A generation mechanism for topside enhanced in coherent backscatter during high-frequency modification experiments in Tromso[J]. Geophysical research letters, 2001, 28(3): 479-482.

刘默然 (1991-),男,河北人,武汉大学电子信息学院博士研究生,研究方向为电离层物理.

周晨 (1983-),男,湖北人,武汉大学电子信息学院副教授,研究方向为电离层物理和电离层电波传播.

赵正予 (1952-),男,吉林人,武汉大学电子信息学院教授、博士生导师,研究方向为电离层物理和电离层电波传播.

Numerical simulation of Langmuir turbulence in the ionosphere heating

LIU Moran ZHOU Chen ZHAO Zhengyu ZHANG Yuannong

(InstituteofElectronicInformation,WuhanUniversity,Wuhan430072,China)

The Zakharov model is used to complete the full-scale simulation study of the generation of topside ionospheric turbulence. At the reflection point of O-mode waves, electromaganetic wave degenerates to two waves: plasma wave and ion acoustic wave. Then, the perturbation of electrons leads to the conversion from O-mode waves into Z-mode waves, and Z-mode waves could propagate into higher area. The result shows that in the millisecond magnitude scale, the Langmuir wave and ion acoustic wave are excited at the reflecton point of O-mode wave, and it leads to locally strong disturbance of electrons. The interaction between waves and particles makes O-mode wave convert into Z-mode wave and Z-mode wave propagates into higher area. In the topside of ionosphere, Z-mode wave excites the parametric decay instability and electrostatic field occurred. This study helps the understanding of the nonlinear interaction between HF wave and plasma in the ionosphere.

heating ionosphere; parametric instability; Langmuir wave; ion accoustic wave

10.13443/j.cjors.2015110602

2015-11-06

国家自然科学基金青年科学基金(41204111)； 国家高技术研究发展计划项目(2013AA***1010A, 2014AA***1010A)

P352.3

A

1005-0388(2016)04-0743-06

刘默然, 周晨, 赵正予, 等. 电离层加热中朗缪尔湍动的数值模拟研究[J]. 电波科学学报,2016,31(4):743-748.

LIU M R, ZHOU C, ZHAO Z Y, et al. Numerical simulation of Langmuir turbulence in the ionosphere heating[J]. Chinese journal of radio science, 2016,31(4):743-748.(in Chinese). DOI: 10.13443/j.cjors.2015110602

联系人： 周晨 E-mail: chen.zhou.whu@gmail.com