非平行分层等离子体鞘套电波传播的复射线方法
张粲宇 叶红霞 付海洋 何鸿飞 梁子长
(1.复旦大学 电磁波信息教育部重点实验室,上海 200433;2.电磁散射重点实验室,上海 200438)
非平行分层等离子体鞘套电波传播的复射线方法
张粲宇1叶红霞1付海洋1何鸿飞2梁子长2
(1.复旦大学 电磁波信息教育部重点实验室,上海 200433;2.电磁散射重点实验室,上海 200438)
基于损耗媒质的复Snell定律提出采用复射线方法研究电磁波在非均匀且非平行分层的等离子体媒质中的传播特性. 该方法考虑非均匀平面电磁波的复射线(包括等幅度面的传播射线和等相位面的传播射线),追踪电磁波复射线在每层媒质中的传播路径以及它们透过媒质分界面时的折射射线,同时根据复射线的传播方向计算电磁波在每层媒质中的传播衰减,数值累计整个传播过程中的传播衰减即可获得电磁波穿过等离子体鞘套的总衰减.由钝锥体仿真流场数据简化出非平行分层几何模型并采用复射线方法进行计算分析. 计算结果表明:飞行器头部至尾部的传播衰减相差巨大且呈现迅速减小趋势,非平行分层非均匀等离子体媒质存在某特定入射角,能使传播衰减达到最小值.
复矢量法;射线追踪;传播衰减;等离子体鞘套
DOI 10.13443/j.cjors.2015090801
引 言
临近空间飞行器(飞船返回舱、弹头等)以超高声速进入大气层时,由于粘性和激波的作用,飞行器周围会形成一个温度高达几千摄氏度的高温区,高温区内分子被分解和电离形成一个包覆飞行器的“等离子体鞘套”. 当电磁波在等离子体中传播时,等离子体不仅会通过反射和折射改变电磁波的传播方向,还会因为带电粒子间的碰撞吸收一部分能量,从而减弱雷达波强度并对雷达波形和极化方向产生影响,对地面测控产生极大干扰. 因此,研究电磁波在等离子体鞘套内的传播特性,对雷达目标跟踪、黑障通信等问题具有重要的理论意义和应用价值.
等离子体问题的研究可以追溯到20世纪50年代,Glick首次提出简化的等离子体微观物理模型,推导了非磁化等离子体的介电常数计算式[1];赵汉章等人在非均匀等离子体密度的双指数分布假设基础上,导出了电磁波穿过等离子体鞘套时的反射及透射系数的解析表达式[2];Gregolre等人从理论上推导了非磁化等离子体中电磁波传输的基本公式,分析了电磁波在等离子体中的吸收因子和透射因子,研究非磁化等离子体包覆物的雷达散射特性[3];Laroussi等用WKB(Wentzel. Kramers. Brillouin)方法计算以任意角入射的电磁波在不均匀等离子体中的衰减,并分析了电磁波在等离子体中的衰减与等离子体碰撞频率、电磁波频率、等离子体最大密度、电磁波入射角的关系[4];Hu等人采用散射矩阵方法(Scattering Matrix Method,SMM)对抛物线和指数型分布的磁化等离子体的反射、透射、吸收进行分析研究[5];Raymond等人提出用时域有限差分(Finite Difference Time Domain,FDTD)法研究等离子体的电波传播问题[6],以及各种对FDTD方法的改进方法,以期提高计算效率[7-10]. Qian等人采用时域积分方程(Time-Domain Integral Equation,TDIE)结合Born近似思想计算了叠加等离子体鞘套后的雷达散射面积(Radar-Cross Section,RCS),可估计等离子体鞘套对RCS的影响[11].
然而,现有对等离子体鞘套内电波传播特性的研究方法中,解析近似的WKB方法和SMM方法往往局限于简化的平行分层模型,如均匀平面或球面分层结构. 对实际分布情况更复杂的等离子体鞘套模型难以适用. 数值方法如FDTD方法和TDIE等,虽然能适用于任意分布的等离子体媒质,但是庞大的存储空间和计算时间需求导致其无法应用于实际电大尺寸问题. 本文提出采用复射线追踪方法研究这种既非平行分层又电大尺寸的等离子体鞘套的电波传播特性.
1 等离子体鞘套的流场分析
高超声速飞行器在再入过程中,周围大气发生强烈的气动加热和材料烧蚀现象,把这种现象称为真实气体效应. 当绕流流场的电离度达到一定程度时,在飞行器周围会形成含有大量自由电子的等离子体包覆流场,即等离子体鞘套.为了数值模拟高速飞行器周围的等离子体流场参数,本文采用七组元(O、N、O2、N2、NO+、NO、e-)的Navier-Stokes气动力学方程和K-ε湍流模型模拟计算获得等离子体参数分布[12-13]. 考虑图1中所示的钝锥体模型(图中白色区域),其尺寸参数如下:钝锥体全长L=0.5 m,底面半径R=0.15 m,侧面倾角φ=7°,钝头为半径r=0.1 m的半球型,攻角β=0°,即飞行方向沿轴向.
由于钝椎体模型几何对称,仿真飞行方向沿轴向,仿真计算的流场分布具有圆周对称性. 本文后面关于钝椎体周围高温等离子体媒质的流场参数和电磁参数的分布图中,都是只显示了过中心轴线的剖面的一半.
图1给出不同飞行速度和高度下模拟计算的电子密度和碰撞频率分布情况.由图可见:钝锥体周围分布有大范围的高温电离媒质,即等离子体媒质. 这些媒质呈非均匀、非平行分层分布,飞行器头部的气体电离和碰撞更明显.飞行速度提高将同时增大电子密度以及碰撞频率,而飞行高度则主要影响碰撞频率. 此外,低空区域由于空气密度大,空气各成分间的碰撞频率更高.
电磁波在非磁化等离子体内传播时,其反射、透射和吸收等物理作用主要由等离子体的相对介电常数决定,而相对介电常数εr与等离子体密度Ne、等离子体频率ωpe、等离子体碰撞频率ν和入射电磁波频率ω0有关,表示为[1]
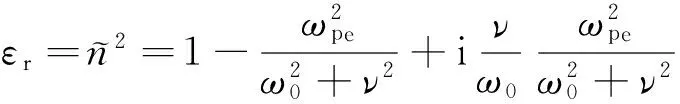
(1)
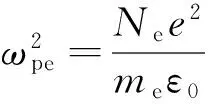
(2)
由数值模拟获得的绕流场参数数据,根据式(1)计算钝锥体周围等离子体媒质的电磁参数. 图2给出了相同飞行条件下(H=50 km、v=15 Ma)三种不同入射波频率对等离子体电磁参数的影响. 可见:入射波频率较低时,鞘套层较厚且密,介电常数呈现很强的等离子体特性;随着入射波频率的提高,鞘套变得更薄,介电常数也相对接近空气. 此外还发现:飞行器头部介电常数的变化往往更加剧烈,且虚部值相比尾部要大得多.
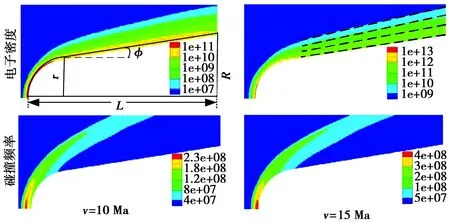
(a) 不同速度下电子密度和碰撞频率的分布(相同高度H=70 km)
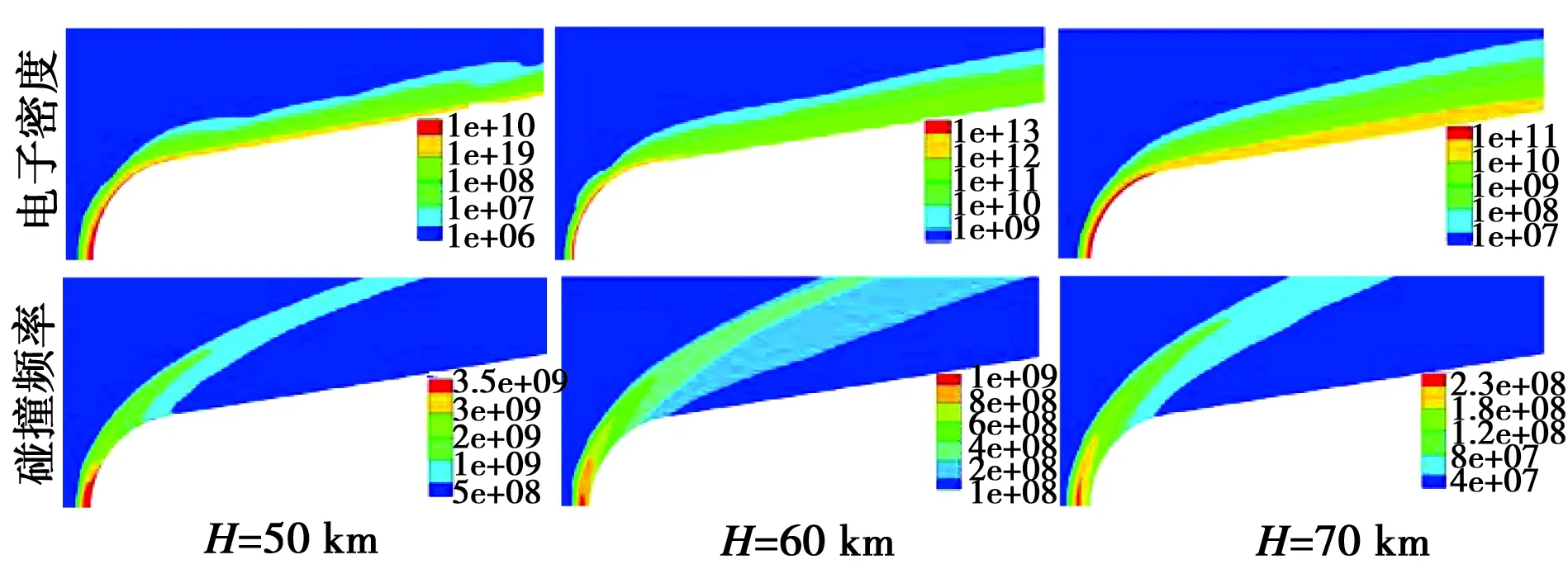
(b) 不同高度下电子密度和碰撞频率的分布(相同速度v=10 Ma)图1 不同飞行条件下流场参数的分布
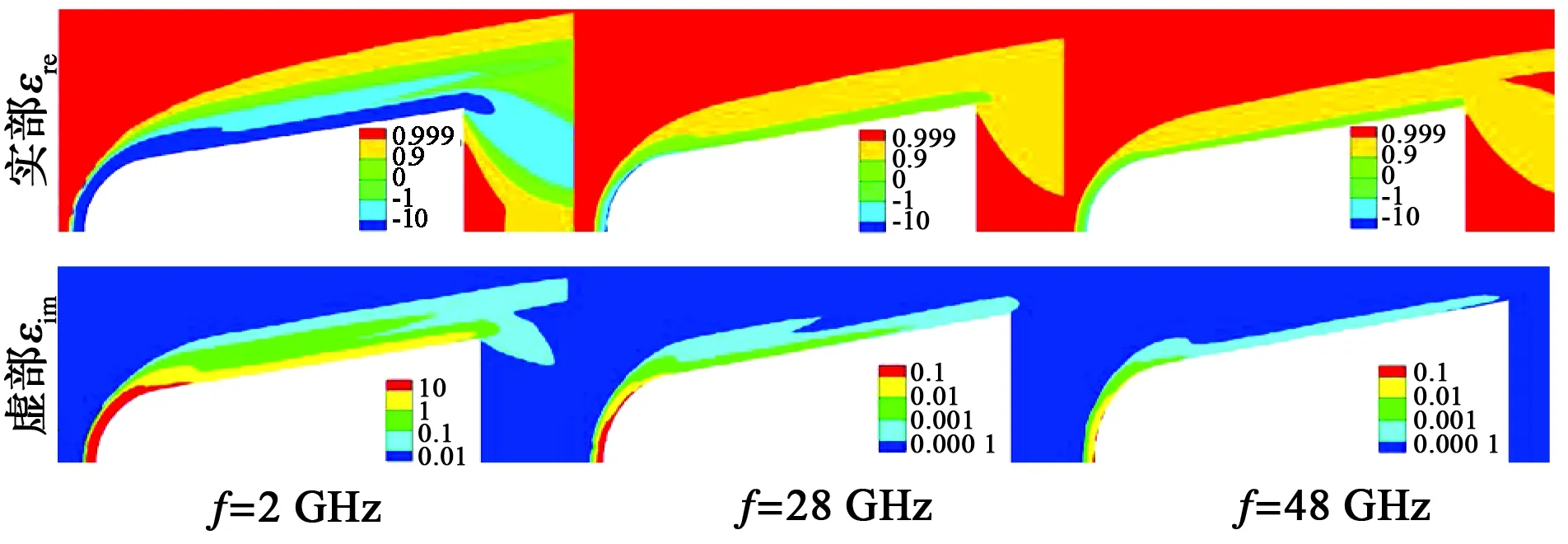
图2 不同入射波频率下介电常数的分布
2 复射线追踪理论
复射线追踪理论[15]从复矢量波动方程理论出发,将损耗媒质中非均匀电磁波波动方程的幅度项与相位项区分考虑,研究复射线(等幅度面射线和等相位面射线)在每层媒质中的传播特性. 在不同媒质的分界面处,则根据复Snell定律(Complex Snell’s Law)确定复透射射线. 下面详细描述复射线追踪方法,以及它在等离子体鞘套媒质层中的应用.
2.1 复射线追踪理论
当均匀平面电磁波由空气进入损耗媒质时,电磁波的等相面与等幅面的传播方向不能重合,变成非均匀平面波,电磁波的传播矢量用复矢量来描述,如电场的复振幅矢量可描述为
E(r)=E0exp(ik·r).
(3)
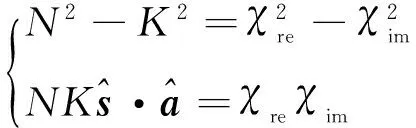
(4)
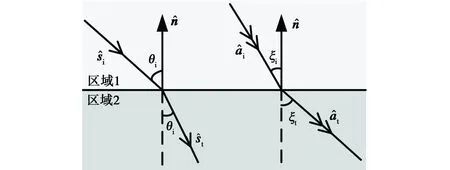
图3 两种损耗媒质分界面的反射与透射
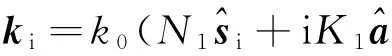
N1sin θi=N2sin θt;
(5)
K1sin ξi=K2sin ξt.
(6)
结合上面式(1)和(4)得到关于N2和K2的计算式为
N1K1sin θisin φi)2=0;
(7)
(χre2χim2-N1K1sin θisin ξi)2=0.
(8)
由式(5)和(6)得到等相面和等幅面的透射角分别为:
聚类分析又称集群分析,它是按“物以类聚”原则研究事物分类的一种多元统计分析方法,它根据样本的多指标、多个观察样品数据,定量地确定样品、指标之间存在的相似性或亲疏关系,并据此联结这些样品或指标,归成大小类群,构成分类树结构图,是分区最常用的方法之一。本研究采用SPSS统计软件进行分类,在一级分区的基础上,完成二级分区。
(9)
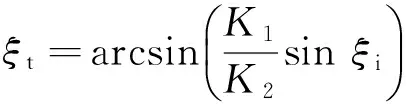
(10)
因此,等相面和等幅面传播的方向矢量为:
(11)
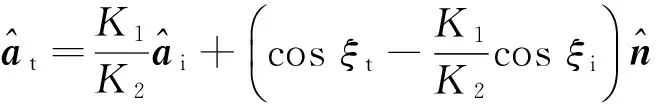
(12)
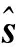
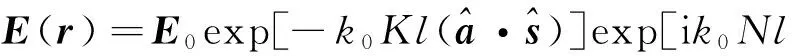
(13)
与式(3)比较可见,沿该路径传播后的传播损耗为
(14)
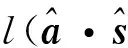
复射线追踪过程中,等相面的追踪路径即电磁波经历不同分层媒质的传播路径,即相位传播的方向,等幅面的方向即电磁波在每层媒质中等幅衰减的方向. 由于该方法数值追踪电磁波在每个媒质分界面以及每层媒质中的电磁波复射线,能适用于任意分层形状的多分层介质模型,克服了传统WKB方法对媒质平行分层的限制,具有更广泛的应用价值,尤其适合高速飞行器周围的非均匀非平行分层的等离子鞘套模型的电磁分析.
2.2 算法验证
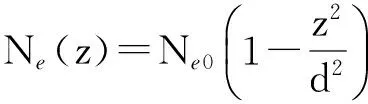
复射线追踪算法和WKB方法计算不同入射波频率和不同碰撞频率下电磁波经过该等离子体层的双程衰减.
复射线追踪算法中,该等离子体媒质模型被平均分成500个离散均匀媒质层进行分析,相邻层之间的分界面处考虑电磁波的折射,实现电磁波的复射线追踪和传播衰减的累计计算. 垂直入射情况下电磁波逐层垂直进入等离子体层,遇到目标后再按原路径垂直返回,电磁波两次经过该等离子体媒质层的总衰减为
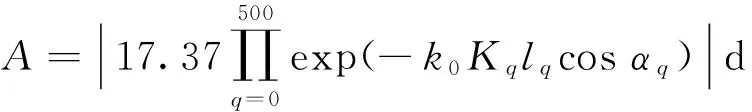
(15)

WKB方法只适用于平行分层的等离子模型,等离子体媒质对电磁波传播的双程衰减可由如下的解析积分计算[19]:
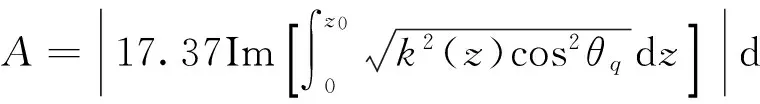
(16)
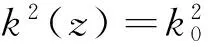
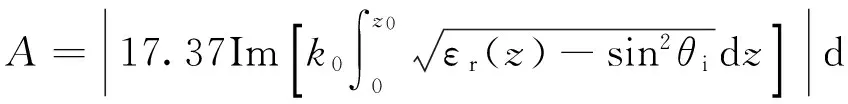
(17)
采用以上两种方法对斜入射(θi=60°)情况下的双程衰减计算结果如图4所示,图中直线为WKB方法的计算结果,圆点为射线追踪方法的计算结果,不同线条对应不同碰撞频率或入射波频率的情况. 结果表明:复射线追踪方法对非均匀平行分布等离子体的双程衰减计算结果与WKB方法的计算结果完全一致,证明了复射线方法用于非均匀等离子体传播计算的可效性. 由于WKB方法只能用于几何平行分层的二维不均匀性等离子体模型,针对非平行分层的等离子体鞘套模型将采用复射线追踪方法进行分析和计算.
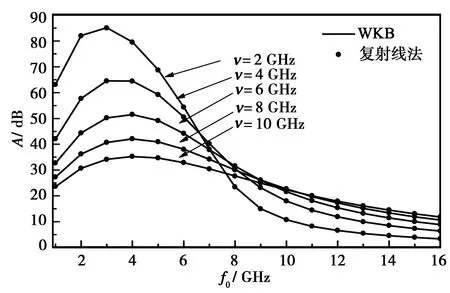
(a) 双程衰减与入射波频率f0的关系
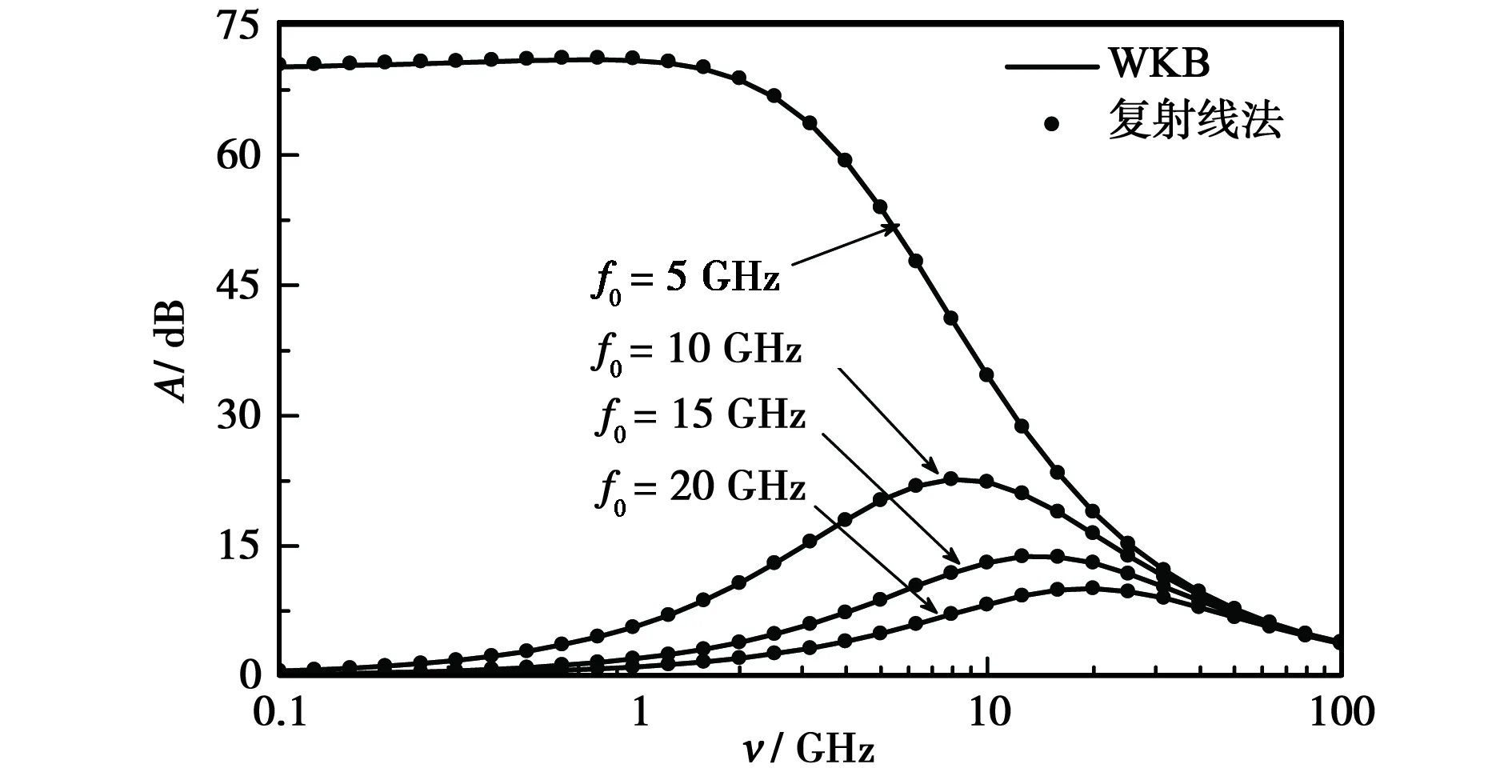
(b) 双程衰减与碰撞频率ν的关系图4 双程衰减与入射波频率f0 、碰撞频率ν的关系
3 等离子体鞘套的传输特性分析
取高度H=50 km、速度v=15 Ma、入射波频率f0=28 GHz的典型再入参数为例[20],其周围的等离子体鞘套折射率虚部χim的分布如图5所示. 考虑图中沿X方向等间隔分布的十个参考点位置,计算电磁波从目标表面位置沿垂直出射方向经过等离子体层的传播衰减. 忽略垂直入射情况下的等离子体分层的轻微不平行分布,将不同位置的流场参数由飞行器表面沿表面法向向外导出,代入平行分层等离子体模型进行计算,其单程传播结果如图6所示.
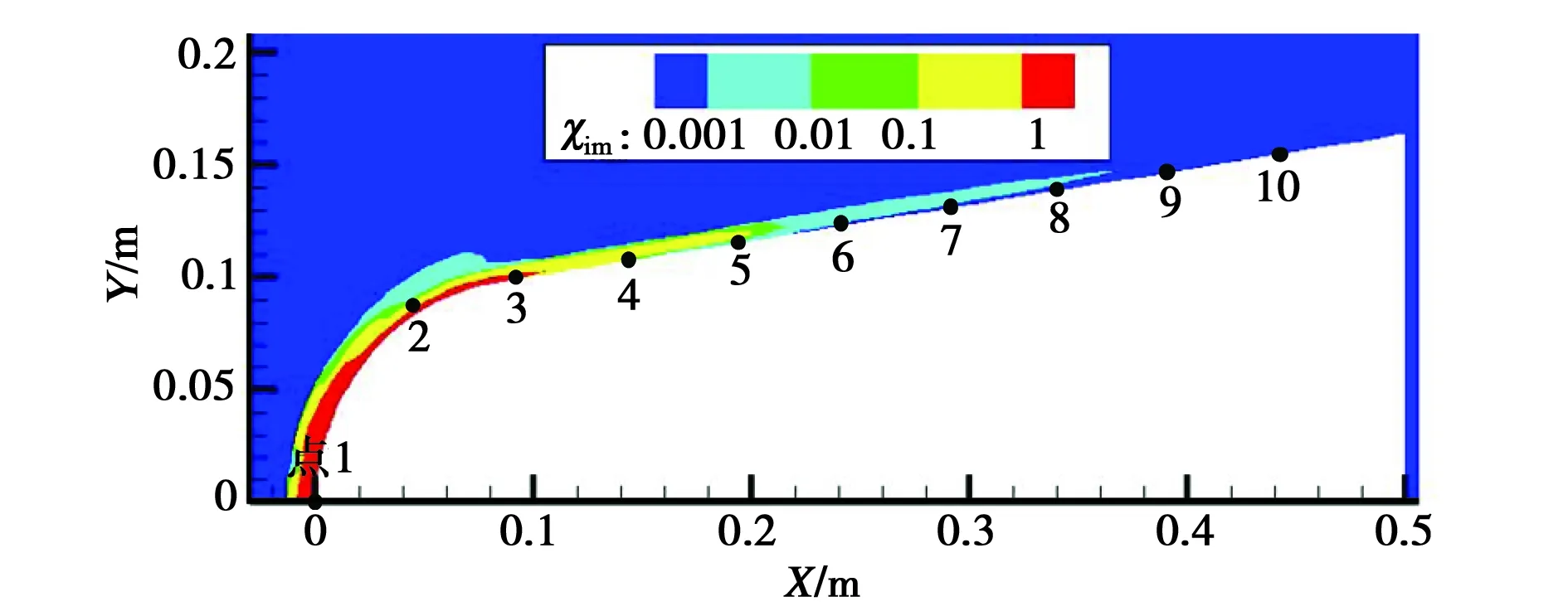
图5 鞘套侧面折射率虚部χim分布及参考点位置
图6的结果表明:随着参考点位置向后,传播衰减迅速减小.在该算例下,自点6(X=0.25 m)起,可以得到较为理想的低传播衰减结果.
为了考虑等离子体鞘套流场实际存在的不平行分布特点以及电磁波入射角度对传播衰减的影响,本文随后将等离子体鞘套离散分层.由图1(b)可以看出:从X=0.1 m起,鞘套层等离子体的电子密度分布可近似为斜劈分层模型. 一般而言,高速钝锥体飞行器周围的鞘套都类似于此种形状. 按图5中相应参考点位置在流场分层处作切线,可将等离子体鞘套模型近似为一顶角Υ=11°的斜劈模型,如图7所示.
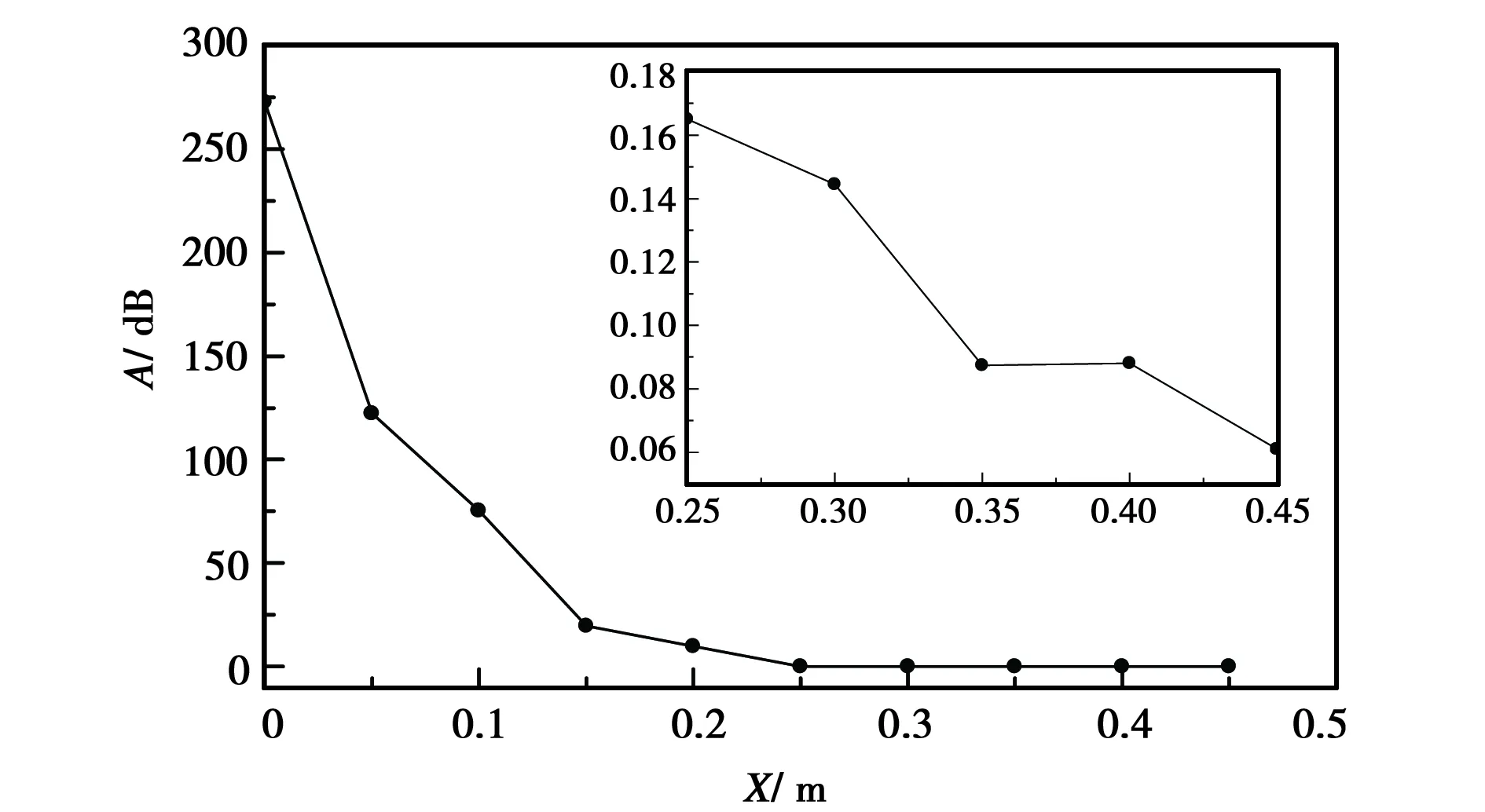
图6 鞘套不同位置的传播衰减
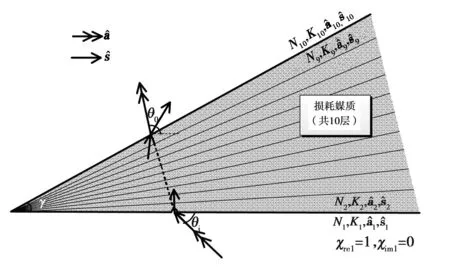
图7 简化几何模型及复射线追踪
本文采用复射线追踪法对靠尾部的媒质区域进行非平行分层媒质的射线追踪和衰减计算. 斜劈等角度间隔地分为10层媒质,每层媒质的电磁参数根据沿钝锥体表面法向向外导出的流场参数计算,入射电磁波从钝椎导体表面沿外法向出发进入等离子体媒质层.之后采用复射线追踪方法追踪电磁波在该非平行分层媒质中的传播路径,并累积计算其总传播衰减.
图8所示的是尾部三个参考点(分别距顶部0.3 m,0.4 m,0.45 m)的传播衰减随电磁波入射角的变化.结果表明:随着入射角度的变化,传播衰减呈现先减小后增大趋势,即存在一个特定的角度使得传播衰减达到最小值. 在该算例中损耗最小角度为85°,进一步研究发现不同入射角度下的各层损耗系数与计入损耗的有效距离都会发生变化,但在85°入射时各层累加的损耗系数与损耗有效距离的乘积是最小的. 针对不同几何模型以及介电常数分布,都存在相应的传播损耗最小角,采用复射线追踪方法可以计算各类等离子体分布下传播衰减最小的角度,为工程上确定发射天线主瓣方向提供参考价值.
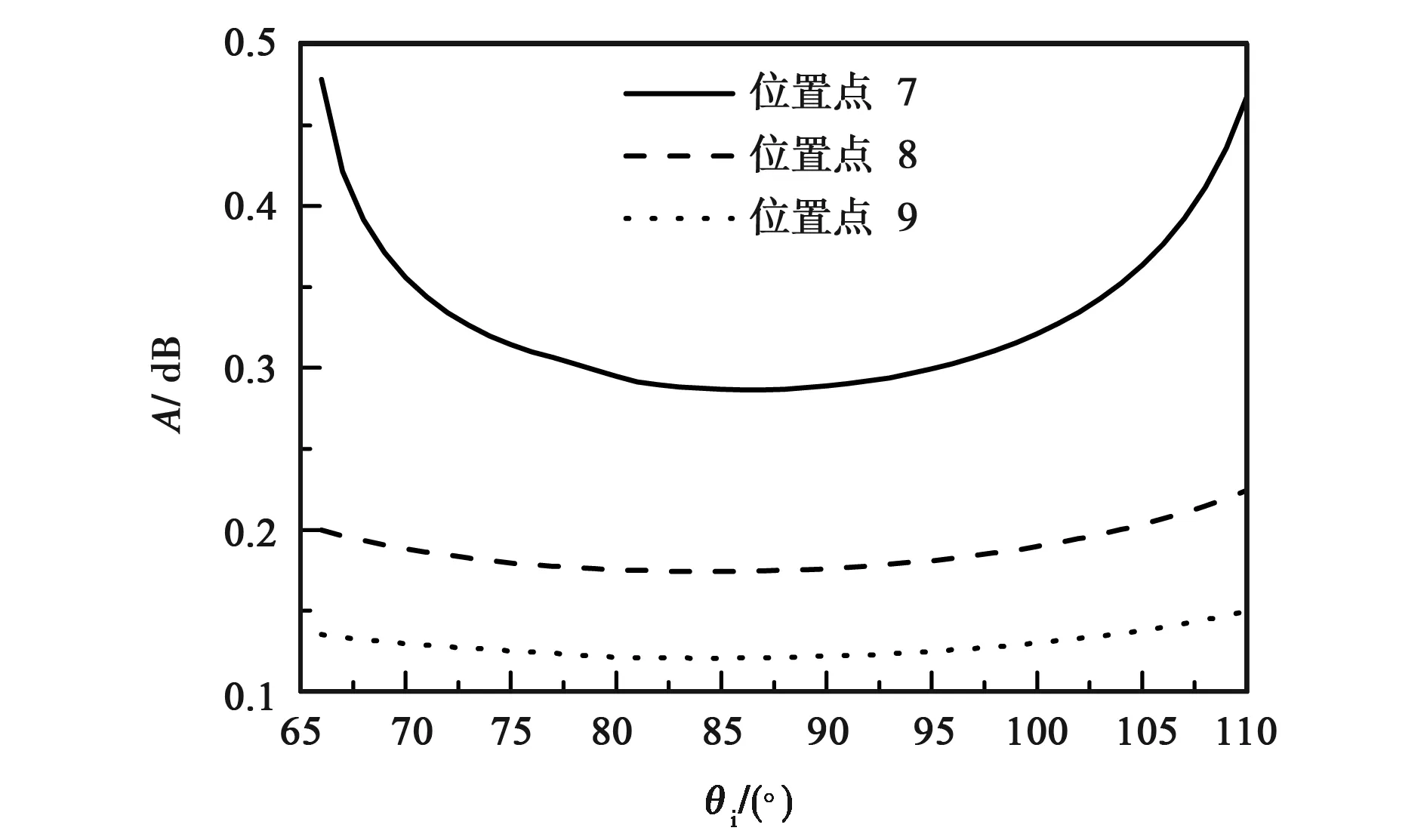
图8 不同入射角度的传播衰减
4 结论与讨论
本文针对等离子体鞘套非均匀且非平行分层的复杂分布特点,基于复Snell定律提出用复射线追踪方法分析每层媒质中电磁波复射线的传播过程,并根据等幅面射线和等相面射线的传播路径数值累计计算电磁波经过等离子体鞘套的传播衰减.该算法可以克服传统的解析WKB方法对平行分层的限制以及FDTD计算复杂度高的缺陷.
本文针对旋转对称的钝椎体再入模型,数值仿真获取再入体周围的流场数据,然后结合流场数据的旋转对称性和大尺度曲面分层特点,利用切平面近似代替大尺度曲面,获得了一个近似的斜劈分层模型,并且每层媒质的电磁参数由仿真的流场数据直接计算.其后本文采用复射线追踪方法对该斜面分层模型进行电磁波传播路径追踪和数值电磁衰减计算. 计算结果表明:钝椎体尾部区域的电波传播衰减相对于头部明显减小;在相同的位置,不同角度的电磁波在等离子体媒质中会因折射经历不同的传播路径,从而引起不同的传播衰减.
[1]GLICK H S. Interaction of electromagnetic waves with plasmas of hypersonic flows[J]. ARS journal, 1962, 32: 1359-1360.
[2] 赵汉章, 吴是静, 董乃涵. 不均匀等离子体鞘套中电磁波的传播[J]. 地球物理学报, 1983, 26(1): 9-16.
ZHAO H Z, WU S J, DONG N H. The propagation of electromagnetic waves in an inhomogeneous plasma sheath[J]. Chinese journal geophysics, 1983, 26(1): 9-16. (in Chinese)
[3]GREGOIRE D J, SANTORU J, SCHUMACHER R W. Electromagnetic wave propagationin unmagnetized plasmas[R]. Washington D C: Air Force Office of Scientific Research, 1992.
[4]LAROUSSI M, ROTH J R. Numerical calculation of the reflection, absorption, and transmission of microwaves by a nonuniform plasma slab[J]. IEEE transactions on plasma science, 1993, 21(4): 366-372.
[5]HU B, WEI G, LAI S L. SMM analysis of reflection, absorption, and transmission from nonuniform magnetized plasma slab[J]. IEEE transactions on plasma science, 1999, 27(4): 1131-1135.
[6]RAYMOND J L, FORREST H, KARL S K. A frequency-dependent finite-difference time-domain formulation for transient propagation in plasma[J]. IEEE transactions on antennas and propagation, 1991, 39(1): 29-34.
[7]莫锦军, 刘少斌, 袁乃昌.非均匀等离子体覆盖目标隐身研究[J]. 电波科学学报, 2002, 17(1): 69-73.
MO J J, LIU S B, YUAN N C. On the stealth effect of non-uniform plasma covered radar targets[J].Chinese journal of radio science, 2002, 17(1): 69-73.(in Chinese)
[8]刘少斌, 张光甫, 袁乃昌. 等离子体覆盖立方散射体目标雷达散射截面的时域有限差分法分析[J]. 物理学报, 2004, 53(8): 2633-2637.
LIU S B, ZHANG G F, YUAN N C. Finite-difference time-domain analysis on radar cross section of conducting cube scatter covered with plasmas[J]. Acta physica sinica, 2004, 53(8): 2633-2637. (in Chinese)
[9]LIU J F, XI X L, WAN G B, et al. Simulation of electromagnetic wave propagation through plasma sheath using the moving-window finite-difference time-domain method[J]. IEEE transactions on plasma science, 2011, 39(3): 852-855.
[10]LI J, GUO L X, JIAO Y C, et al. Composite scattering of a plasma-coated target above dispersive sea surface by the ADE-FDTD method[J]. IEEE geoscience and remote sensing letters, 2013, 10(1): 4-8.
[11] QIAN J W, XIA M Y. Simulation of scattering by a rotating hypersonic object with plasma sheath[C]//IEEE International Conference on Computational Electromagnetics(ICCEM). Hong Kong, February 2-5, 2015:258-260.
[12]李江挺, 郭立新, 金莎莎, 等. 等离子体鞘套中的电波传播特性研究[J]. 电波科学学报, 2011, 26(3): 494-499.
LI J T, GUO L X, JIN S S, et al. EM wave propagation characteristic in plasma sheath[J]. Chinese journal of radio science, 2011, 26(3):494-499. (in Chinese)
[13]常雨, 陈伟芳, 罗宁, 等. 基于物理光学法的再入等离子体包覆体空间散射特性分析[J]. 微波学报, 2008, 24(2): 1-6.
CHANG Y, CHEN W F, LUO N, et al. Analysis of the spatial scattering characteristic for the reentry target cloaked by plasma based on the physical optics method[J]. Journal of microwaves, 2008, 24(2): 1-6. (in Chinese)
[14]常雨. 超声速/高超声速等离子体流场数值模拟及其电磁特性研究[D]. 长沙: 国防科技大学, 2009.
CHANG Y. The study of the supersonic/hypersonic plasma flow numerical simulation and its electromagnetic characteristics[D]. Changsha: National University of Defense Technology, 2009. (in Chinese)
[15]CHANG C Y, PETER J G, HOPCRAFT K I. Ray tracing in absorbing media[J]. Journal of quantitative spectroscopy and radiative transfer, 2005, 96: 327-341.
[16]DUPERTUIS M A, PROCTOR M, ACKLIN B. Generalization of complex Snell-Descartes and Fresnel laws[J]. Journal of the optical society America, 1994, 11(3): 1159-1166.
[17]郑浩, 叶红霞, 徐丰. 基于双向射线追踪的损耗介质目标散射技术[J]. 电波科学学报, 2015, 30(5):896-902.
ZHENG H, YE H X, XU F. Extended bi-directional analytical ray tracing algorithm for lossy dielectric object[J]. Chinese journal of radio science, 2015, 30(5):896-902.(in Chinese)
[18]孙爱萍, 李丽琼, 邱孝明, 等. 电磁波与非磁化等离子体的相互作用[J].核聚变与等离子体物理, 2002, 22(3): 135-138.
SUN A P, LI L Q, QIU X M, et al. Interaction of the electromagnetic waves and non-magnetized plasmas[J]. Nuclear fusion and plasma physics, 2002, 22(3): 135-138. (in Chinese)
[19]刘少斌, 袁乃昌, 莫锦军. 等离子体隐身技术[M]. 北京: 科学出版社, 2005.
[20]刘嘉兴. 飞行器测控通信工程[M]. 北京: 国防工业出版社, 2010.
[21]刘少斌, 莫锦军, 袁乃昌. 非磁化等离子体密度与目标雷达隐身的关系[J]. 电波科学学报, 2003, 18(1): 57-61.
LIU S B, MO J J, YUAN N C. Research on the relation between the unmagnetized plasma density and the stealth of target[J]. Chinese journal of radio science,2003,18(1):57-61. (in Chinese)

张粲宇 (1992-),男,江西人,复旦大学电磁波信息科学教育部重点实验室研究生,主要研究方向为WKB近似和等离子体鞘套传播等.

叶红霞 (1976-),女,江苏人,复旦大学信息科学与工程学院副教授.已发表论文40 余篇,出版专著一本.曾获教育部自然科学一等奖.研究方向为计算电磁学、粗糙面散射与遥感、散射与逆散射等.
EM wave propagation in non-parallel plasma sheath using complex ray tracing algorithm
ZHANG Canyu1YE Hongxia1FU Haiyang1HE Hongfei2LIANG Zichang2
(1.KeyLaboratoryforInformationScienceofElectromagneticWaves,Shanghai200433,China; 2.ScienceandTechnologyonElectromagneticScatteringLaboratory,Shanghai200438,China)
This paper introduces a complex ray tracing algorithm based on the complex Snell law to investigate the electromagnetic wave propagation in Reentry Plasma Sheath with non-uniform and non-parallel stratification. The algorithm takes the non-uniform electromagnetic complex rays (including propagation ray of equal-amplitude plane and equal-phase plane) into account, traces the path of complex rays in every layer and the refract rays in each interface. The attenuation is calculated along the direction of equal-amplitude plane in each layer and the total attenuation through the entire propagation path can be obtained by accumulate the attenuation in each layer. This paper further analyzes non-parallel stratified plasma sheath model with the complex ray tracing algorithm. Numerical results show that the attenuation sharp decreases from the top of aircraft to the tail. There exists a specific incident angle with minimum attenuation in non-parallel stratification layer.
complex vector; ray tracing; propagation attenuation; plasma sheath

10.13443/j.cjors.2015090801
2015-09-08
国家自然科学基金(No.61001007, 41404122); 教育部科技支撑基金
TN011;P354
A
1005-0388(2016)04-0625-07
张粲宇, 叶红霞, 付海洋, 等. 非平行分层等离子体鞘套电波传播的复射线方法[J]. 电波科学学报,2016,31(4):625-631.
ZHANG C Y, YE H X, FU H Y, et al. EM wave propagation in non-parallel plasma sheath using complex ray tracing algorithm[J]. Chinese journal of radio science,2016,31(4):625-631. (in Chinese).DOI: 10.13443/j.cjors.2015090801
联系人: 叶红霞 E-mail:yehongxia@fudan.edu.cn

