利用教材瑕疵有效开发例(习)题
邓艳奎游运泉张立志
利用教材瑕疵有效开发例(习)题
邓艳奎1游运泉2张立志2

教材是呈现教学内容的载体,是承载课程观、教学观的重要教学资源,也是教材开发专家的心血,但教材难免有不尽人意的地方。正是这些瑕疵激发了我校课题组开发例(习)题的灵感,拓宽了我们的视野,为我们开发例(习)题提供了方法和途径。我们对发现的教材中例(习)题的瑕疵进行了分析和利用,变瑕疵为资源,有效地开发了例(习)题。下面谈谈我们的做法和体会。
一、寻找瑕疵
对中小学数学教材进行例(习)题开发研究,就是要使教材中的例(习)题内容更符合教学实际,更贴近学生的真实生活。教材中例(习)题的瑕疵是有价值的教学资源,也是我们研究的着力点、切入点和生长点。因此,我们对教材中的例(习)题进行了挑刺。
首先是钻研教材。主要是吃透教材的编排意图,理解知识板块之间的联系,分析知识点在各阶段的分布与衔接,避免出现无理取闹的挑刺。其次是大胆质疑。我们对教材例(习)题的编排顺序、逻辑关系进行盘点梳理,对例(习)题的呈现形式和表述进行分析解读,对知识点和学生的认知水平进行对照比较,试图寻找瑕疵。第三是主研人员有意识地在教学过程中求证瑕疵。只有通过教学实践,才能找准瑕疵,保证资源的价值。第四是给瑕疵分类。分类能为剖析和有效利用瑕疵奠定基础。把瑕疵作纵横向比较,能确定瑕疵资源的地位和作用,找出瑕疵的纰漏和问题所在,为开发找到着力点。
我们在研究中,把教材例(习)题中的瑕疵资源分为三类。
一是不紧密瑕疵资源,就是指在编排顺序上存在逻辑关系不紧密问题的例(习)题。如,人教版三年级下册教材在讲授小数初步认识后,安排了一道狼、羊和菜同船过渡的拓展练习题。(下称案例1)又如,人教版八年级下册《教师教学用书》的四边形一章末有这样一道测试题:如图1,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9。则该梯形的面积是()。(下称案例2)

图1

二是不严谨瑕疵资源,就是指在表述上不严谨,内容上不切教学实际的例(习)题。有表述上不严谨的简单问题,如把足球的拼块说成是正五边形或正六边形。还有内容上不切教学实际的问题。如,人教版三年级下册教材第8单元“问题解决”中的第7题(图略):根据题目提供的信息,要求一年要产生多少垃圾,先求出我家三口人一个月产生多少千克垃圾,根据一年有12个月,再求出12个月一共可以产生垃圾多少千克。(下称案例3)又如,人教版七年级下册教材复习题七中的第8题(图略):△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=50°,∠C=70°,求∠DAC、∠BOA。(下称案例4)
三是不正确瑕疵资源,就是指在例(习)题中或在推理中有明显的瑕疵或有明显问题的例(习)题。如,人教版八年级下册教材中有这样一段话:“比较一般平行四边形的对角线和菱形的对角线,你会发现,菱形的对角线把菱形分成四个全等的小直角三角形,而一般的平行四边形只被分成了全等的两对三角形,一对是锐角三角形,一对是钝角三角形。”(下称案例5)。又如,人教版四年级下册教材中的练习七第10题(如图2所示),我们可以发现:题目说的是每层7间教室,图中每层只有6间,且第一层中间还设有大门通道。(下称案例6)

图2
二、琢磨瑕疵
我们认为,要剖析瑕疵资源,首先必须把握好课标,要以学生认知水平为基础,从教学目标入手,以知识结构为线索,以发展学生十大数学能力为宗旨,反复推敲,仔细斟酌,以免出现新的瑕疵。
案例1中,我们认为狼、羊和菜同船过渡的拓展练习与本章学习内容联系不够紧密,应调至推理与分析的相关章节。(现行教材采用)
案例2中,编者的设计意图是:“通过梯形的常用辅助线(过顶点作对角线的平行线)。利用平行四边形的判定和性质,将梯形的面积转化为三角形的面积,实现图形的变换,是平行四边形和梯形的综合应用。”我们认为本题的4个备选答案中没有一个选项是符合题目要求的,不能达到编者的设计意图。
案例3中,计算过程超出学生当前的计算能力,影响了学生解决问题的效果。37×3=111千克,111×12=?千克,三位数的乘法超出了学生知识储备。
案例4中,∠A=50°的表述,在此题中明显不当,应改写为∠BAC=50°。
案例5中,我们认为,后半句有一瑕疵。
若图3中的∠NME>90°。则△MGF与△ENG是一对全等的钝角三角形。而△MNG与△EFG也是一对全等的钝角三角形。
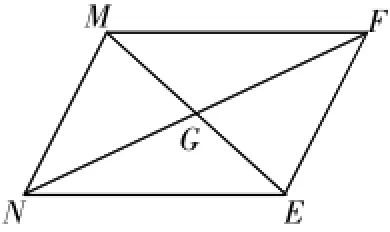
图3
可见,一般平行四边形只被分成了全等的两对三角形,一对是钝角三角形,另一对三角形的形状不确定。问题的症结在于:不能仅凭∠MGN和∠EGF是锐角,就判断△MNG和△EGF是一对锐角三角形,而要看△MNG和△EGF中最大角的大小。
案例6中,习题插图有明显错误:每层7间,图中每层只有6间,第一层中间还设有大门通道,如果利用运算定律进行计算,显然需要改造。
三、激活瑕疵
使瑕疵成为例(习)题开发的资源,还需要我们进行探索与实践。尝试开发的前提是紧扣教学目标。如果改变了教学目标,就会造成知识体系混乱,违背学生的认知规律。因此因材施教、另辟蹊径是变瑕疵为例(习)题开发的资源的有效途径。
如在案例3的二次开发中,我们设计了如下思路。①一人一年可以产生多少千克垃圾?37×12=444(千克)。②3人一年共产生多少千克垃圾?444× 3=1332(千克)。这样就绕过了原来的知识障碍。
对于有明显失误的例(习)题,我们引导学生找错,培养学生的批判意识。发现问题后,组织学生讨论如何修改,如何解答。学生由于思维活跃,生活背景有差异,修改的结果往往是百花齐放,从而达到开发例(习)题之目的。如在教学案例6时,在老师的提醒下,学生发现图中每层只有6间教室。在问题驱使下,学生积极思考。这时老师指出:如果题中没有每层7间教室这个条件,你还可怎么编题?有的学生把每层教室的数量换成了6、7、8、9等,分别列式为25×6×4,25×7×4,25×8×4,25×9×4,利用乘法交换律先算25×4=100,结果一目了然。在学生兴致正浓时,老师又提醒:从图上看,是不是所有房间都可以摆放课桌椅?作为通道的房间是不能摆设桌椅的,那么怎样列式计算?(25×6×3+25×5等)如果在前面列式的基础上又该如何计算?(25×6×4-25)比较列出的两种算式,你发现哪种列式便于运用运算定律计算?这样处理,学生不仅牢固地掌握了连乘算理,而且在解决实际问题中理解了运用运算定律的方便与快捷。
从上述的分析和研究中我们不难看出,教材中例(习)题的瑕疵为有效开发例(习)题提供了着力点和生长点。教师如果在钻研教材、把握课标的前提下,用智慧和汗水去琢磨,定能让知识的明珠更加璀璨夺目。(本文系常德市立项课题《义务教育阶段数学教材例(习)题二次开发与应用研究》CDJYKY2014阶段成果)
(作者单位:1.临澧县杨板中学2.临澧县四新岗中学)

