考虑杆塔风险概率的输电线路巡检路径优化方法
李铭钧,甘团杰,赖奎,黄耀升,郑海,李锦焙,何瑞文
(1.广东电网有限责任公司江门供电局,广东江门 529030;2.广东工业大学,广东广州 510006)
考虑杆塔风险概率的输电线路巡检路径优化方法
李铭钧1,甘团杰1,赖奎1,黄耀升1,郑海1,李锦焙2,何瑞文2
(1.广东电网有限责任公司江门供电局,广东江门 529030;2.广东工业大学,广东广州 510006)
针对实际输电线路的结构,同时考虑巡检距离和杆塔风险等级为目标函数,提出一种差分纵横交叉算法(DECSO),用于解决输电线路巡检路径优化问题。该算法通过对巡检路径进行寻优,同时兼顾杆塔风险概率,形成一条最优路径,使得在巡检距离最短的同时,保证了输电线路可以安全稳定运行。基于DECSO算法,采用Matlab仿真软件对一个具有20个杆塔的输电线路网络进行了仿真研究。将仿真结果和其他算法的结果进行比较,结果表明了算法在解决输电线路巡检路径的可行性和优越性。
输电线路;巡检;差分纵横交叉算法;风险概率
输电线路是电力系统的重要组成部分,其安全稳定运行为电力系统可靠、稳定运行提供了重要保障。目前,对输电线路方面课题的研究大部分都集中在输电线路故障评估和定位方面[1-2],而对于输电线路巡检路径规划的研究甚少[3-4]。由于输电线路及其附属设备长期暴漏在野外,缺乏相应的保护,正因为输电线路的这种运行方式,使得输电线路巡检作为保证电力输电线路安全可靠运行的一项基础性工作,受到供电部门的重视[5-7]。
传统的人工巡检缺乏效率和科学性,使得输电线路风险不能及时发现和排除。传统的人工巡检方法巡检路径没有经过优化,使得巡检效率不高,而且没有将杆塔的风险概率考虑在内。通过巡检路径优化来制定输电线路巡视路径,可以有效提高巡检效率和节省费用,所以输电线路巡视路径优化是必要的。
目前输电线路巡视路径规划算法主要是人工智能算法,如改进遗传算法等。文献[8]提出基于遗传算法的改进A*算法(RAT*)应用于输电线路巡检路径规划,虽然该算法具有良好的寻优搜索能力,但其在路径优化时容易陷入局部最优,无法得到最优路径。文献[9]中提出改进的遗传算法对输电线路无人机巡检路径进行优化,由于遗传算法对巡检路径进行优化过程中容易陷入局部最优,往往会导致无法获得巡检路径的全局最优解。文献[10]提出将机器人用于高压架空线路巡检,并为此对机器人能源在线补给做了相应的研究。文献[11]提出采用大型无人直升对输电线路进行全自动巡检。文献[12]提出如何对无人机输电线路巡检平台的选择。
本文对输电线路巡视路径规划模型进行改进,通过贝叶斯分类器模型[13-16]原理建立杆塔风险概率模型,在已知杆塔周边影响因素的情况下,求出杆塔的风险概率,同时考虑杆塔风险概率和巡检路径距离具体的条件下建立巡检路径模型。本文所用算法是差分纵横交叉算法,这种算法是差分进化算法和纵横交叉算法的混合算法。仿真部分是利用20个杆塔的输电线路模型,通过仿真实验验证差分纵横交叉算法在解决输电线路巡检路径优化问题的有效性和可行性。
1 输电线路巡检路径优化分析
在该系统中,在对巡检路径进行优化的同时,考虑巡检路径距离和杆塔的风险概率。一般情况下,存在安全隐患的输电线路杆塔往往分布在不同的输电线路上,当对这些存在安全隐患的杆塔进行检查时,不能沿固定的输电线路进行巡检。为了及时有效地消除输电线路运行隐患和快速完成巡检任务,需要寻找1条满足需求的最优巡检线路,该线路就必须同时满足2个条件:一是保证巡检距离最短,即最快完成巡检任务;二是要保证巡检路径时尽可能优先处理风险概率较高的杆塔,由于输电线路受分布范围广,环境条件复杂以及本身状态不尽相同因素影响,风险的概率也就不尽相同。则同时考虑风险概率和巡检路径距离的输电线路巡检路径优化模型为
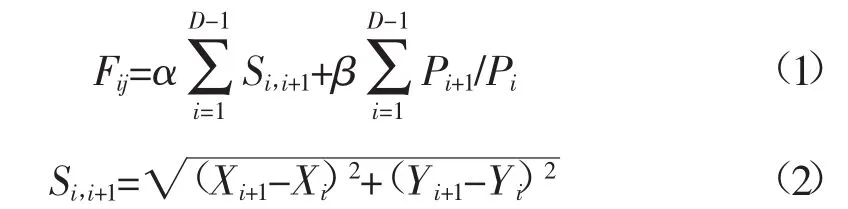
式中:Fij为目标函数;D为待巡检杆塔数目;Si,i+1为1条巡检路径中2个相邻杆塔之间的距离,为了方便研究,本文采用2个杆塔坐标之间的距离替代实际巡检路径的距离;Xi、Yi分别为第i个杆塔的横坐标和纵坐标;Pi、Pi+1分别为杆塔i和i+1的风险概率;α和β为加权系数,当巡检过程要求时间和距离短则提高系数α的值,同理若要求优先处理风险高的则相应提高系数β的值。
2 杆塔风险概率模型
2.1 输电线路杆塔运行风险分类
构建输电线路运行状态样本集合不仅需要考虑每1个线路杆塔本身的因素,而且还要考虑到杆塔所处位置的周围环境因素,包括自然因素、人为因素的影响。由于在不同地点、不同时期影响杆塔风险概率的主要因素不尽相同,因此,要达到快速准确地排除杆塔的安全隐患,那么就要综合考虑各种因素对杆塔运行状态的影响。
为了可以全面准确地评估输电线路杆塔风险概率,选取了对输电线路设备的运行情况影响较为突出的几项因素作为评估杆塔风险的关键指标,即输电线路杆塔所在地区天气情况、输电线路杆塔役龄即运行时间、输电线路杆塔所在地区近几年极端天气发生频率、输电线路杆塔所在地区地质因素、输电线路杆塔使用材料等级、输电线路杆塔运行异常频率、输电线路杆塔上次巡检至今的巡检天数和指当前杆塔所在输电线路电力负荷等各项因素来综合考虑。
2.2 输电线路杆塔风险概率模型
杆塔风险概率是输电线路巡视路径目标函数中的一项指标,同时也是杆塔运行状态的一项参考数据。每个杆塔风险运行概率受到天气因素、地质状况、人为因素、线路电压等级、杆塔所处位置、杆塔材料、异常频率、材料等级和历史负荷等因素影响。将每种对杆塔风险运行概率的影响因子用C1到C9来表示,E表示决策属性,也就是表示杆塔的运行状态,因此形成初始决策如表1所示。
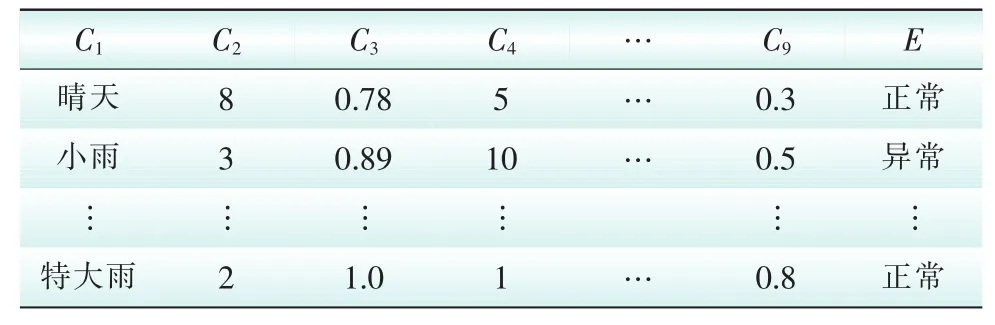
表1 初始决策表Tab.1 Initial decision-making table
表1中的部分数据是经过量化后得出的结果,其量化过程是将每种影响因素的特征映射到一定的区间内,并用具体的数值表示其中的不同特征。利用贝叶斯网络模型计算得出初始决策表中每个属性的条件概率,然后通过概率计算即可得出样本的高风险运行概率。
其中线路状态量B=(B1,B2)=(异常,正常),则有P(B1)=0.508,P(B2)=0.492。则该预测样本的运行风险的概率为
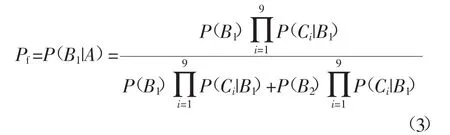
式中:P(Bi|A)为样本A属于B1类型的概率;P(Ci|B1)与P(Ci|B2)为在不同类别情况下,样本各属性取不同值的概率。
同理该样本的正常概率为
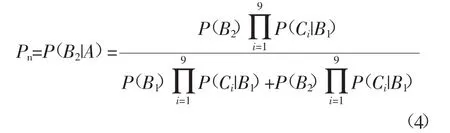
预测样本所属的类型为计算得到的Pf与Pn之间的大值。
3 差分纵横交叉算法
3.1 纵横交叉算法
纵横交叉算法(crisscross optimization algorithm,CSO)[17]是一种新的智能随机搜索算法,该算法采取特殊的纵横搜索策略,即横向交叉和纵向交叉2组搜索机制。通过结合1个简单的竞争机制,使得横向交叉和纵向交叉完美地结合起来:交叉后产生的子代,与其父代进行竞争,只有比父代适应度更好的子代才会被保留下来,竞争后得出的解称为占优解[18]。正是由于CSO采用这样的搜索机制,使得CSO相对于目前常用的智能优化算法具有收敛精度高、计算速度快的特点,特别适用于求解复杂的优化问题。具体流程如下。
1)初始化种群。
2)求出每个粒子的适应度和种群全局最优解。
3)执行横交叉操作,并计算适应度执行竞争操作。
4)执行纵交叉操作,并计算适应度执行竞争操作。
5)如果迭代次数达到算法设定的迭代次数,则结束算法,否则转到步骤2)继续执行。
3.2 横向交叉算子
设D为待巡检杆塔数目,M为种群大小,B是1-D之间的一个随机排列向量,no1和no2分别为B中的2个粒子编号,X(no1,j),X(no2,j)分别是父代种群中个体粒子X(no1)和X(no2)的第j维,MShc(no1,j)和MShc(no2,j)分别是X(no1,j),X(no2,j)通过横向交叉生成中庸解的第j维,DShc为横向交叉产生的占优解。
步骤如图1所示。

图1 纵横交叉算法横向交叉流程Fig.1 Horizontal crossover operation process
与遗传算法不同,CSO算法中的横向交叉以较小概率在超立方体(如图2所示)外缘进行搜索,这种跨界搜索机制区别于遗传算法的交叉操作,有效地增强了算法的全局搜索能力[19]。
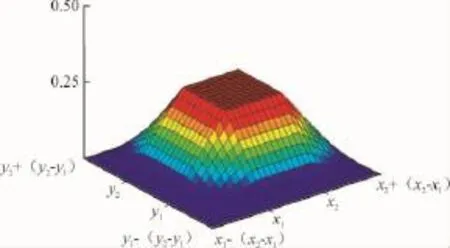
图2 二维空间的概率分布Fig.2 Distribution of probability density of the moderation solutions for 2-D space
3.3 纵向交叉算子
纵向交叉算子是1个解的不同维度算数运算,这种运算可以使陷入局部最优的种群跳出,然后快速收敛到全局最优。
设D为待巡检杆塔数目,M为种群大小,B是1-D之间的一个随机排列向量,纵向交叉概率为Pvc,no1和no2分别为B中的2个杆塔编号,X(j,no1),X(j,no2)分别是父代种群中个体粒子X(j)的第no1维和第no2维,MSvc(j,no1)是X(j,no1),X(j,no2)是纵向交叉生成中庸解的第j维,DSvc为纵向交叉产生的占优解。
具体步骤如图3所示。

图3 纵横交叉算法纵向交叉流程Fig.3 Vertical crossover operation process
3.4 竞争算子
竞争算子是一种淘汰机制,它的作用是将2代种群中的粒子进行对比,只有当子代粒子比父代粒子的适应度更强时才能代替父代粒子参与下一次迭代。这样的竞争机制使得种群朝向最优方向进化。具体流程如图4所示。

图4 竞争算子的流程Fig.4 Competitive operator process
3.5 基本的差分进化算法
差分进化(differential evolution,DE)[18-20]算法是由Rainer Storn和Kenneth Price于1996年共同提出的一种优化算法。其基本原理是:利用种群个体间的差分向量来对个体进行扰动以达到个体突变的目的,通过交叉变异策略产生新个体。差分进化算法主要包含突变操作,交叉操作和选择操作3个步骤。
设D为待巡检杆塔数目,M为种群大小,Pd为差分算法交叉概率,Xn01、Xn02和Xn03分别为种群中3个互不相同的粒子,F为缩放因子,p为(0,1)之间的一个随机数,EV(i,j)为第i个粒子生成试验向量的j维,MSdc(i,j)为第i个粒子生成中庸解的j维,DSdc为差分进化算法产生的占优解。具体步骤如图5所示。

图5 差分进化算法流程图Fig.5 Differential evolution operation process
3.6 DECSO混合算法在巡检线路优化中的应用
基本纵横交叉算法(CSO)具有非常强大的全局搜索能力和收敛速度,而差分进化算法具有良好的局部扰动能力。差分纵横交叉算法融合了基本的纵横交叉算法强大的全局搜索能力和差分进化算法的局部扰动变异能力,使得混合算法在具有更优的全局搜索能力的同时,具有良好的收敛速度。由于DECSO具备非常好的的全局搜索能力,同时具有良好的收敛速度,使得DECSO成为解决输电线路巡检路径优化问题的一种非常有效的方法。本文采用DECSO解决巡线路径优化问题正是基于DECSO的这一特点。流程图如图5所示。
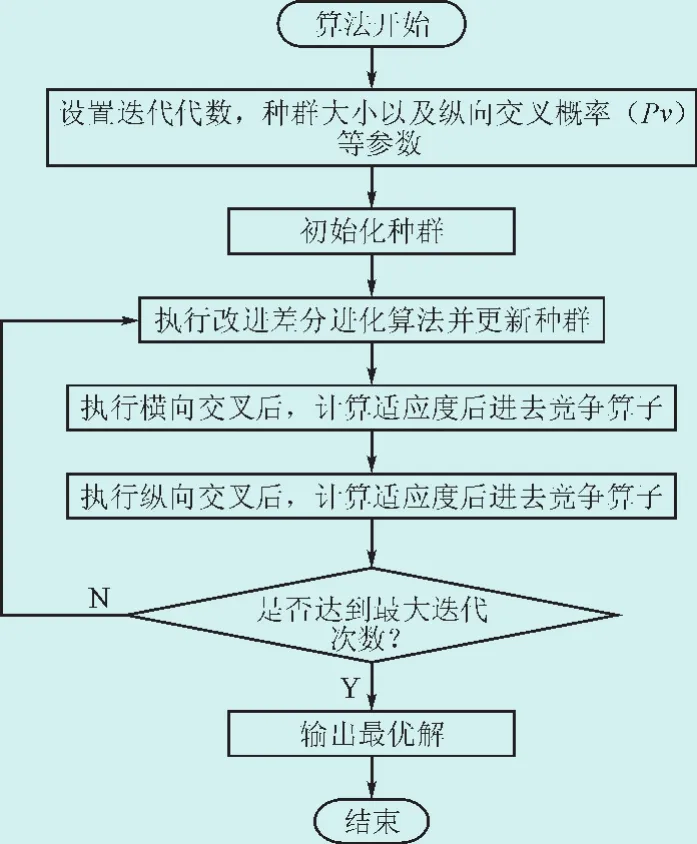
图6 差分纵横交叉算法流程图Fig.6 The flow chart of DE-CSO algorithm
4 仿真分析
为了验证本文提出的DECSO算法的可行性,对1个20个杆塔的输电线巡检模型来进行仿真计算。本文的仿真均运行在Intel CPU G3240、4.0 GB内存、32位Windows 7操作系统和Matlab 2010环境中。
本案例以表2的20组数据作为仿真对象,采用DECSO算法对该案例进行仿真,仿真参数设置种群规模为100,迭代总数设为1 000,采用DECSO算法的输电线路巡检路径在不同权值下的优化结果如表3所示。
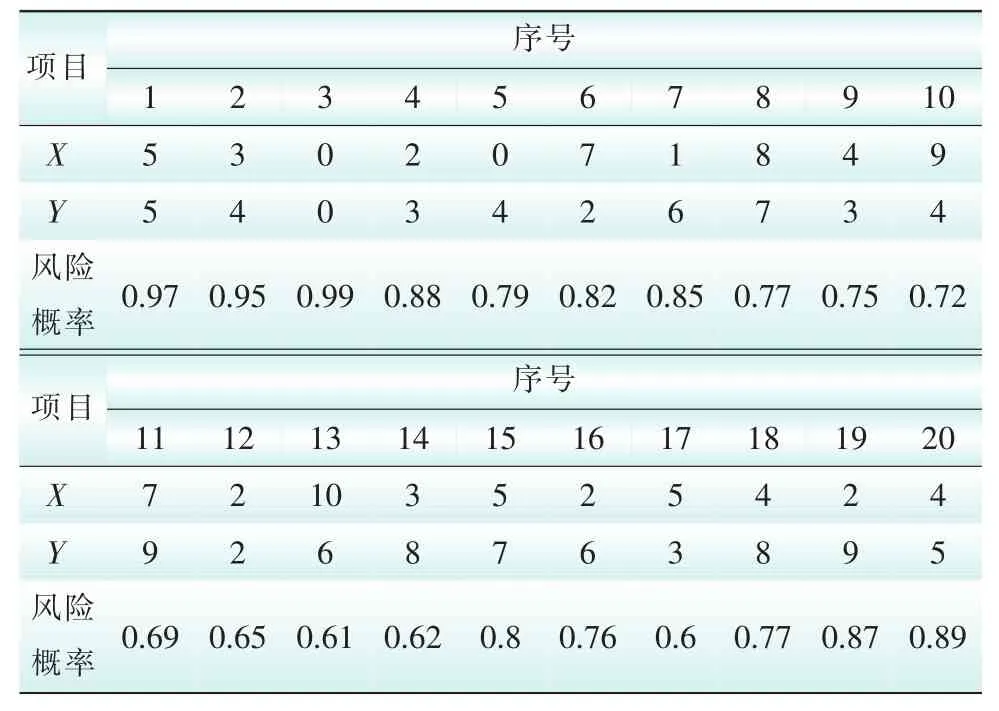
表2 20杆塔系统参数表Tab.2 The data of 20-steel tower transmission network

表3 在不同权值下的最优解Tab.3 The optimal solutions with different weights
表3为在不同权值的情况下,通过差分纵横交叉算法得到的最优路径,特别当α=0,β=1和α=1,β=0时最优路径如表所示,Fij分别为1.79和39.55。当α=0,β=1的时候意味着在路径寻优过程仅仅考虑风险因素。当α=1,β=0时意味着仅仅考虑距离而忽略风险概率。根据上表给出的结果可以知道仅仅考虑距离得到的优化结果是仅仅考虑风险的优化结果的23倍,这意味着距离因素对目标函数的影响是风险概率因素的23倍,为了可以平衡风险概率和距离因素对巡检路径的影响,所以权值β应为权值α的23倍,根据最新的权值得到的优化结果如表4所示,路径图如图7所示。

表4 综合考虑风险概率和路径距离的最优解Tab.4 The optimal solution of considering both the inspection distance and the risk probabilities of steel towers
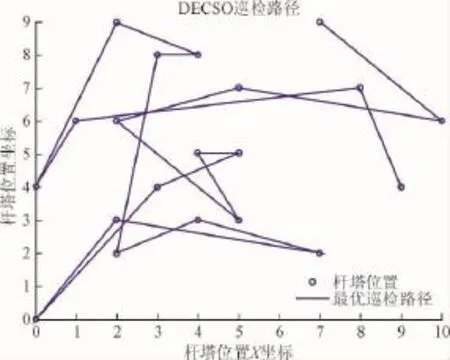
图7 最优路径图Fig.7 The diagram of the optimal patrol route
当α=0.04,β=0.96时,优化结果为4.800,该优化结果虽然比α=0,β=1的大,但是考虑的因素更加全面。
根据表1中提供的输电线路杆塔坐标位置和风险概率,分别用原始遗传算法(genetic algorithm,GA)、原始粒子群算法(PSO)和差分纵横交叉算法(DECSO)进行对比,其中权值设置为α=0.04,β= 0.96,PSO算法的参数设置如下种群规模为100,迭代次数为1 000,搜索空间为20%,惯性权重为0.6。GA算法的参数设置为:群体大小为100,进化代数1 000,交叉概率0.7,变异概率为0.005。DECSO算法的参数设置为:种群规模为100,迭代总数设为1 000,纵向交叉概率Pvc为0.75。为得出巡视路径和目标函数综合值如表5所示。

表5 不同算法下的巡视路径比较Tab.5 Comparison with different algorithms on inspection paths
由表5可知,在同时考虑输电线路杆塔运行风险概率和巡检距离的情况下,DECSO,GA和PSO算法的优化结果分别是4.8,5.91和5.66,可以看出DECSO的效果明显优于其他2种算法,说明DECSO算法用于输电线路巡检路径优化是有效的。
为了更好地验证DECSO算法在解决输电线路巡检路径优化问题的可行性,本实验用DECSO算法、PSO算法和GA算法在同样条件下对巡检路径优化做50组独立实验验证,其稳定性如表6所示。其中参数设置和表5实验一样。
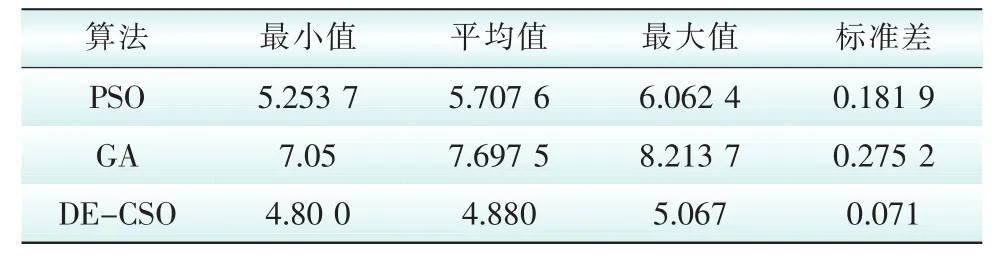
表6 不同算法应用于路径寻优的稳定性Tab.6 Stability of the path optimization with different algorithm applied
分别采用DECSO、PSO和GA对输电线路巡检路径优化单独做50次实验得到的最小、最大值、平均值和标准差如表6所示,可以看出,DECSO在最大值、最小值优于PSO和GA,可见DECSO算法在解决该巡检系统具有更高的精度,DECSO算法结果的标准差也比PSO和GA的小,显示DECSO在稳定性方面同样优于PSO和GA。所以采用DECSO解决输电线路巡检路径优化问题是可行的[20-21]。
5 结语
本文在DECSO算法的环境下搜索含有20个杆塔的输电线路巡检路径得出以下结论:
1)在同时考虑杆塔风险概率和巡检距离的条件下,与其他算法相比,DECSO算法具有较强的搜索能力和较好的稳定性。
2)输电线路巡视路径优化模型为科学的安排输电线路巡检提供了依据。
3)本文没有将DECSO算法应用于大规模(100个杆塔以上)巡检路径优化问题,考虑到DECSO算法具备强大的全局搜索能力和良好的收敛速度,所以将DECSO算法应用于大规模的输电线路巡检路径优化问题将会是一个很好的研究方向。
[1]刘明军,邵周策,上官帖,等.输电线路山火故障风险评估模型及评估方法研究[J].电力系统保护与控制.2016,44(6):82-89.LIU Mingjun,SHAO Zhouce,SHANGGUAN Tie,et al.Study on models and methods of risk assessment of transmission line fault caused by fire[J].Power System Protection and Control,2016,44(6):82-89(in Chinese).
[2]李冰然,夏临闽,赵晶晶.基于模糊评价和风险矩阵的输电线路风险评估[J].电力与能源,2014(6):672-677.LI Bingran,XIA Linmin,ZHAO Jingjing.Fuzzy evaluation and risk matrix based on overhead lines risk assessment[J].Power&Energy,2014(6):672-677(in Chinese).
[3]刘珂宏,刘亚东,盛戈皞,等.基于输电线路全工况信息的风险评估方法[J].高压电器,2016(3):23-28.LIU Kehong,LIU Yadong,SHENG Gehao,et al.All conditions information based risk assessment method for transmission line[J].High Voltage Apparatus,2016(3): 23-28(in Chinese).
[4]王涛,李澄.一种混合输电线路故障测距新方法[J].江苏电机工程,2015(5):17-20.WANG Tao,LI Cheng.Research on the Jiangsu shortcircuit current limiting strategy during UHV construction period[J].Jiangsu Electrical Engineering,2015(5):17-20(in Chinese).
[5]王平,李琳.输电线路雷击灾害风险层进式评估体系的构建[J].电瓷避雷器,2016,44(6):82-89.WANG Ping,LI Lin.Study on models and methods of risk assessment of transmission line fault caused by fire[J].Insulators and Surge Arresters,2016,44(6):82-89(in Chinese).
[6]路永玲,刘洋,高嵩,等.江苏电网2005至2013年架空输电线路雷击跳闸分析及防护[J].电瓷避雷器,2015(1):46-53.LU Yongling,LIU Yang,GAO Song,et al.Analysis of lightning trip and protection measures of overhead transmission lines in jiangsu power grid from 2005 to 2013[J].Insulators and Surge Arresters,2015(1):46-53(in Chinese).
[7]马御棠,曹晓斌,王磊,等.雷电参数与地形结合的输电线路绕击闪络率计算[J].电瓷避雷器,2015(1):79-86.MA Yutang,CAO Xiaobin,WANG Lei,et al.Calculation of the transmission line shielding failure trip rate by combination the lightning parameters and terrain parameters[J].Insulators and Surge Arresters,2015(1):79-86(in Chinese).
[8]段其昌,周华鑫,程有富,等.贝叶斯网络在输电线路运行状态预测中的应用[J].计算机科学,2012,39(3): 83-87.DUAN Qichang,ZHOU Huaxin,CHENG Youfu,et al.Application of bayesian network in transmission lines running state prediction[J].Computer Science,2012,39(3):83-87(in Chinese).
[9]郝震,张健,蔡满意.自适应遗传算法在飞行器离线航迹规划中的应用[J].电光与控制,2010,17(1):65-68.HAO Zhen,ZHANG Jian,CAI Manyi.Application of adaptive genetic algorithm in aircraft off-line route planning[J].Electronics Optics&Control,2010,17(1):65-68(in Chinese).
[10]乌小锋.750 kV/330 kV混压同塔四回路输电线路电流不平衡度计算与分析[J].电网与清洁能源,2015,31(1): 52-59.WU Xiaofeng.Calculation and analysis of level of the unbalance current in the 750 kV/330 kV four-crcuit transmission line on one tower[J].Power System and Clean Energy,2015,31(1):52-59(in Chinese).
[11]周风余,温龙旺,苏鹏,等.高压输电线路巡检机器人能源在线补给装置的研制[J].电网与清洁能源,2010,26(1):18-23.ZHOU Fengyu,WEN Longwang,SU Peng,et al.Development of on-line energy supply device for high-voltage transmission linesiterative inspection robot[J].Power System and Clean Energy,2010,26(1):18-23(in Chinese).
[12]彭向阳,钱金菊,麦晓明,等.大型无人直升机电力线路全自动巡检技术及应用.南方电网技术,2016(2): 24-31.PENG Xiangyang,QIAN Jinju,MAI Xiaoming,et al.Automatic powerline inspection technology oflarge unmanned helicopter and its application[J].Southern Power System Technology,2016(2):24-31(in Chinese).
[13]王柯,彭向阳,陈锐民,等.无人机电力线路巡视平台选型[J].电力科学与工程,2014(6):46-53.WANG Ke,PENG Xiangyang,CHEN Ruimin,et al.Unmanned aerial vehicle platform selection for overhead transmission line inspection[J].Electric Power Science and Engineering,2014(6):46-53(in Chinese).
[14]周忠宝,董豆豆,周经伦.贝叶斯网络在可靠性分析中的应用[J].系统工程理论与实践,2006,26(6):95-100.ZHOU Zhongbao,DONG Doudou,ZHOU Jinglun.Application of bayesian networks in reliability analysis[J].Systems Engineering-theory&Practice,2006,26(6):95-100(in Chinese).
[15]霍利民,朱永利,张在玲,等.贝叶斯网络在配电系统可靠性评估中的应用[J].电工技术学报,2004,19(8): 113-118.HUO Limin,ZHU Yongli,ZHANG Zailing,et al.Bayesian networks application to reliability evaluation of electric distribution systems[J].Transactions of China Electrotechnical Society,2004,19(8):113-118(in Chinese).
[16]杨莉,孙华昕,朱宏超.基于贝叶斯网络的多目标优化算法[J].华北电力大学学报,2007,34(1):128-131.YANG Li,SUN Huaxin,ZHU Hongchao.Multi-objective optimization algorithm based-on Bayesian networks[J].Journal of North China Electric Power University,2007,34(1):128-131(in Chinese).
[17]MENG A,CHEN Y,YIN H,et al.Crisscross optimization algorithm and its application[J].Knowledge-based Systems,2014(67):218-229.
[18]李超,谭火超,孟安波,等.纵横交叉算法在电力大客户细分中的应用[J].电气应用,2015(17):58-61.LI Chao,TAN Huochao,MENG Anbo,et al.Application of crisscross optimization algorithm in power customer segmentation[J].Electrical Application,2015(17):58-61(in Chinese).
[19]孟安波,卢海明,李海亮,等.纵横交叉算法优化FCM在电力客户分类中的应用[J].电力系统保护与控制,2015,43(20):150-154.MENG Anbo,LU Haiming,LI Hailiang,et al.Electricity customer classification based on optimized FCM clustering by hybrid CSO[J].Power System Protection and Control,2015,43(20):150-154(in Chinese).
[20]刘晓倩,董新伟,杨瑞静.输电线路防雷措施的仿真与分析[J].电瓷避雷器,2012(4):64-68.LIU Xiaoqian,DONG Xinwei,YANG Ruijing.Simulation and analysis on lightning protection measures of transmission lines[J].Insulators and Surge Arresters,2012(4):64-68(in Chinese).
[21]罗大强,唐军,许志荣,等.10 kV架空配电线路防雷措施配置方案分析[J].电瓷避雷器,2012(5):113-118.LUO Daqiang,TANG Jun,XU Zhirong,et al.Analysis on configuration scheme of 10 kV overhead distribution line lightning protection measure[J].Insulators and Surge Arresters,2012(5):113-118(in Chinese).
(编辑 董小兵)
Power Transmission Line Inspection Planning Optimization Considering Risk Probabilities of Steel Towers
LI Mingjun1,GAN Tuanjie1,LAI Kui1,HUANG Yaosheng1,ZHENG Hai1,LI Jinbei2,HE Ruiwen2
(1.Jiangmen Power Supply Bureau,Guangdong Power Grid Co.,Ltd.,Jiangmen 529030,Guangdong,China;2.Guangdong University of Technology,Guangzhou 510006,Guangdong,China)
Aiming at the structure of the transmission line,and with the patrol inspection distance and risk probabilities of the steel tower taken as the objective function,this paper proposes a DECSO hybrid method to address the optimization of transmission line inspection planning.Through the optimization of the inspection path and taking into account of the risk probability of the steel tower,the algorithm as indicated in the method helps to find an optimal path to minimize the inspection distance and ensure the safe and stable operation of transmission lines as well.The proposed method is implemented on MATLAB and validated on a transmission network consisting of 20 steel towers.And the simulation results are compared with the results by other algorithms,and the results show that the algorithm is feasible and advantageous in solving the transmission line inspection path.
transmission line;inspection;differential evolution crisscross optimization algorithm;risk probabilities
国家自然科学基金资助项目(51377026);广东省电网公司科技项目(GDKJ00000009)。
Project Supported by the National Natural Science Foundation of China(51377026);Science and Technology Program of Guangdong Power Grid Co.,Ltd.,(GDKJ00000009).
1674-3814(2016)10-0061-07
TM73
A
2016-03-18。
李铭钧(1965—),男,硕士,高级工程师,主要研究方向电力企业管理;
甘团杰(1978—),男,硕士,高级工程师,主要研究方向输变电生产管理;
赖 奎(1970—),男,硕士,高级工程师,主要研究方向输变电生产管理;
黄耀升(1983—),男,本科,工程师,主要输电线运行与维护;
郑 海(1987—),男,本科,助理工程师,主要研究方向输电线路运行与维护;
李锦焙(1989—),男,硕士研究生,主要研究方向为智能算法在电力系统中的应用;
何瑞文(1969—),女,博士,副教授,主要研究方向是电力系统继电保护。

