心中有“问”，深思大“获”——浅谈在中职数学教学中对学生质疑能力的培养

江苏省昆山第二中等专业学校　于文荣

心中有“问”，深思大“获”——浅谈在中职数学教学中对学生质疑能力的培养

江苏省昆山第二中等专业学校于文荣

本文结合教学实例，从巧设疑、巧引导、巧点拨三个角度探讨了在中职数学教学中有目的、有计划地培养学生的质疑能力，以引导学生有疑有思，深思大获。

高中数学课堂教学质疑能力

《朱子全书·读书法》中这样说道：“读书无疑者，须教有疑；有疑者，却要无疑，到这里方是长进。”朱熹以病疑喻读书之疑，说明读书要有长进须经历“无疑者须教有疑”“有疑者，却要无疑”两个阶段。而今，现代心理学研究也证实了朱熹的见解：勇于质疑问难、寻根究底，能使大脑皮层处于亢奋状态，是一切思维的导火索。可见，让学生学会思考、学会质疑的重要性。然而，中职学生的学习能力比较弱，需要中职教师在教学中有目的、有计划地去适时引导，才能让学生敢于质疑、善于质疑。那么，在中职数学教学中，教师该如何培养学生的质疑能力呢？笔者从如下几方面进行了有益探索：

一、巧设疑，在“疑”中发展思维

人，生来都是好奇的。在教学中，教师可以积极营造质疑氛围，给学生思考和质疑的空间，提高学生的主动学习意识。在过程中，学生可以通过自主思考、小组合作等形式进行有效探究，使学生的思维活动在良好的质疑环境中得到充分发展。

比如，在“等差数列”的教学中，一位学生突然提出：能把等差数列定义中的“差”改成“和”吗？笔者在充分肯定这位学生“奇思妙想”的基础上，组织学生以小组合作探究的形式来论证，在强烈的探索动机中让学生自主验证，当学生验证等差数列定义中的“差”字能改成“和”时，学生的脸上充满了惊喜。

可见，一个有价值的质疑，让学生经历了猜想、探究、验证的思维过程，使一个原本枯燥的数学定义变得富有趣味和有意义，不仅提高了学生的猜想意识，也有效发展了学生的数学思维。

二、巧引导，在“疑”中积极思维

新课改在强调学生是学习主人的同时也强调了教师的引导作用。在培养学生质疑能力的过程中，教师应积极做好自己的启发者和点拨者的角色，要千方百计地使学生的脑子转起来，名副其实地成为质疑的主人。

例如，在平面α内有∠BAC，已知P埸α，∠PAB=∠PAC。求证：点P在平面α内的射影在∠BAC的平分线上。

证明：如图，作PO⊥α，PE⊥AB，PF⊥AC，连接OE，OF，OA。先求证△PAE≌△PAF，AE=AF，再根据AB奂α，PO⊥α，得出PO⊥AB，AB⊥OE。同理AC⊥OF。最后得出△AOE≌△AOF，即∠EAO=∠FAO，在命题得证的基础上，教师可以引导学生在学习小组内合理改编问题，对自己学习小组中的合作成员进行“发难”，这对提高学生的数学思维能力大有裨益，摘录部分学生的改编题如下：

变式1：如果三角形所在平面外一点与三角形三个顶点的连线，与三角形任意一角的两边夹角为锐角且相等，那么这点在三角形所在平面内的射影是三角形的内心。

变式2：如果三角形所在平面外一点，到三角形三个顶点距离相等，那么这点在三角形所在平面内的射影是三角形的外心。

在上述过程中，学生在逐一的自编和自评中解决每一道例题，在教师的启发下，一题变多变，让学生体会到了主动参与、积极思考的快乐与成功。

三、巧点拨，在“疑”中深化思维

问题并非越多越好。学生的质疑能力毕竟是有限的，这就需要教师在让学生鼓起勇气提出质疑时，也要对学生做到适时巧妙的点拨，引导学生“深”问，只有有价值的“疑”才能深化学生的思维，具有培养学生创新精神的意义所在。

以《直线的方程》一课的教学为例，首先呈现例题：过点P（3，2）作直线l与x轴，y轴正半轴交于A，B两点，给出相应的条件，求直线的方程。学生以小组学习的形式自编了如下题目：

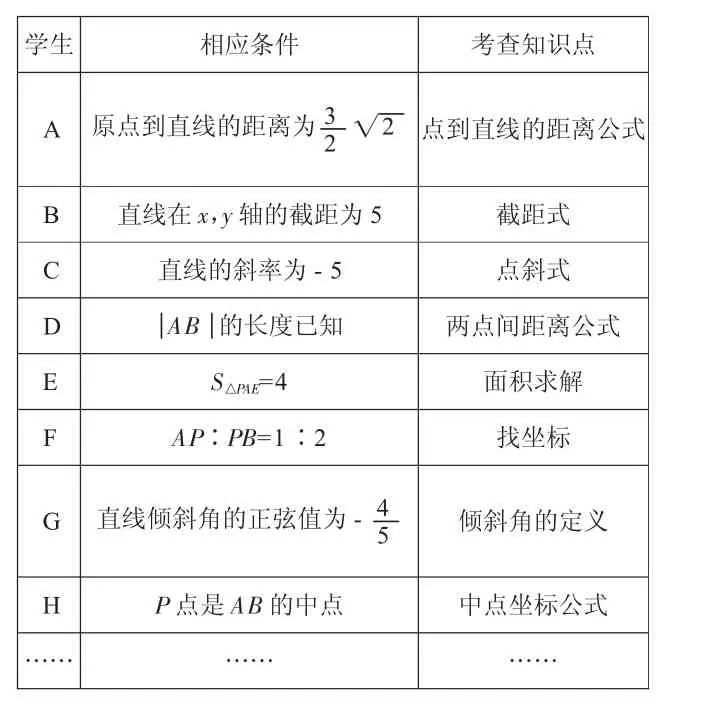
学生　相应条件　考查知识点A　原点到直线的距离为3姨　点到直线的距离公式22 B的长度已知　两点间距离公式E S△PAE=4　面积求解F　AP∶PB=1∶2　找坐标B　直线在x，y轴的截距为5　截距式C　直线的斜率为-5　点斜式DA G　直线倾斜角的正弦值为-4 5　倾斜角的定义H　P点是AB的中点　中点坐标公式……　……　……

在学生给出的条件基础上，笔者又适时增加了有点深度的条件：①S△ABC最小；②原点到直线l的距离最大；③|OA|+|OB|最小。面对这些条件，学生开始质疑：“这里的最大，最小怎么确定呢？”在教师即时的转换角度、适时点拨下，学生的质疑意识已经有了深一层的飞跃。

总之，“质疑”是思维的开端，是促进学生从“学会”转向“会学”的关键。只要我们能够坚持不懈，将质疑能力的培养置于课堂教学的每个适宜的环节中，设疑引思，逐步引导，注重启发，那么在一段时间之后，一定能让学生学贵有疑，有疑才有思，贵比触深思，深思大获之。

[1]陈娇容.质疑能力的培养[J].科教文汇.2013.18：131-132

[2]沈怡.谈中职学生数学问题意识的培养[J].新校园.2013.5：50-52

[3]徐新新.数学思想在高中数学教学中的应用[J].数学学习与研究.2011.42：42