轨道交通车辆车体垂向弯曲频率优化研究

王玉杰

(长春轨道客车股份有限公司研发中心,130062,长春∥工程师)



轨道交通车辆车体垂向弯曲频率优化研究

王玉杰

(长春轨道客车股份有限公司研发中心,130062,长春∥工程师)

轨道交通车体轻量化是降低运营能耗、减轻轮轨间动力作用的重要手段,但车体轻量化使得车体模态频率下降,致使车体弹性振动加剧,增加结构共振的风险。研究表明,通过优化承载结构来提高整备状态下车体模态频率的效果非常有限。提出运用承载结构模态频率和整备状态质量来估算整备状态下车体模态频率的公式,以及通过下吊设备弹性悬置实现大幅提高车体整备状态垂向弯曲频率的方法,并给出悬置质量与整备状态频率的关系式。运用有限元分析模型对关系式的验证表明,简化估算公式具有很高的准确性,对车体垂向弯曲频率的优化具有指导意义。

轨道交通车辆； 车体； 整备状态模态频率

Author′s address Development Center of Changchun Railway Vehicles Co.,Ltd.,130062,Changchun,China

随着三维设计软件、有限元分析及结构优化技术的普遍使用,实现轨道车辆车体承载结构轻量化对于制造企业而言已不再困难。车体轻量化技术是降低运营能耗、减轻轮轨间动力作用的重要手段。然而,过分追求结构的轻量化,往往会导致车体刚度不足、车体模态频率下降,当车辆以较高速度运行及线路条件较差时,车体的弹性振动加剧,从而极大地影响车辆的乘坐舒适度,并直接或间接地影响到系统结构部件的疲劳及车辆运营的安全[1-4]。在追求车体轻量化的同时,如何最大化地提高车体的模态频率一直是车辆设计的难点。本文将探究能够提升铁道车辆车体模态频率的有效措施。

1 车体模态频率及其对平稳性的影响

车体作为列车与旅客的直接界面,承担着为旅客提供安全、舒适、便捷空间的重要任务。由于车体支撑在转向架之上,持续受到由轨道经转向架传来的振动,如何保证旅客及车体本身结构的安全,并尽可能地实现振动噪声舒适性的最大化,是车辆制造商不懈追求的目标。避免车体结构共振是实现该目标的基本要求。为避免共振,UIC 566《客车车体及其零部件载荷》规范规定:要识别、描述处于5～40 Hz范围的车体振动模态,并且车体的自振频率应该有别于自转向架传递至车体的振动频率。EN 12663《铁道车辆车体结构要求》规范在振动模态一节中规定“整备状态下,车体的自振模态应该与悬挂频率充分分离,或者解耦”,以避免发生共振响应现象。此外,国外大多要求整备状态下车辆的垂向弹性振动频率不低于规定值,并且与转向架振动频率有一定差值。例如:德国ICE车技术任务书中规定,中间车整备状态下车体的最低自振频率不允许低于10 Hz,弯曲振动频率和转向架点头及浮沉振动的频率比值不得低于1.4；瑞典 X 2000型摆式列车要求车辆系统各部位间的固有频率差在3 Hz以上；法国国营铁路要求转向架的振动频率不与车体弯曲振动频率相耦合,分隔范围希望在1.0～1.5 Hz。可见,UIC 566及EN 12663规范对于车体在整备状态下垂向弹性振动频率的要求是定性的,而各国根据运营和车辆自身的情况,对车体弹性频率的要求进行了量化。

我国TB/T 1335—1996《铁道车辆强度设计及试验鉴定规范》4.1.2中规定:在各种载荷条件下,车体的自振频率不同于转向架的蛇行、点头等振动频率,从而在整个运用速度范围内避免共振现象。该规范在8.9节的振动试验中建议测定车辆及其重要部件的5～40 Hz范围内的自振频率,并要求“车体自振频率应不同于转向架所传递给车体的振动频率,而且符合4.1.2的要求”。可见,TB/T 1335—1996规范中关于车体动态特性的规定与UIC 566规范基本一致。随着我国铁路运营速度的迅速提高,原铁道部于2001年印发了《200 km/h及以上速度级铁道车辆强度设计及试验鉴定暂行规定》。其6.4.1节中规定“整备状态车体弯曲自振频率与转向架点头和浮沉自振频率的比值≥1.4,并且整备状态车体最低弯曲频率不得低于10 Hz”。这是我国对高速列车车体模态频率的明确成文规定。研究表明,在车辆各模态中,垂向弯曲频率对车辆振动及舒适性影响最大。车体垂向弯曲模态频率越小(即车体的垂向刚度越小),车体中部弹性振动越剧烈,当车体垂向一阶弯曲频率提高到一定数值后,车体弹性对平稳性的影响趋于稳定。该数值的确定与车辆运行速度和轨道不平顺质量相关[1,5]。

2 承载结构对车体模态参数的影响

对于车辆制造商而言,总是设法在保证车辆运营性能的同时尽量减重,以实现制造成本的降低。但减重往往导致车体模态频率下降。提高车体模态频率的措施包括减少车门数量、减小车体长度、提高侧墙高度等。而运营商为了提高运营效率,总是希望增加车体长度和车门数量,保证地板面高度。在限界限制下,地板面高度决定了车体侧墙高度不能随意提高,这使得设法通过车体结构的改变提高模态频率的难度大为增加。

为解决上述问题,另外的思路是对车体关键承载结构进行尺寸优化,以提高车体承载结构模态频率[6]。图1为承载结构边梁厚度对车体模态频率的影响,可见,当边梁厚度由3 mm增加到15 mm后,车体承载结构的一阶垂向弯曲频率增加了0.606 Hz,而菱形变形频率却降低了0.890 Hz[6]；在整个计算过程中,一阶横向弯曲、一阶呼吸与一阶扭转模态频率则均呈小幅上涨然后下跌的趋势。因而,增加边梁厚度,仅能略微增加承载结构的一阶垂向弯曲频率,但同时会降低菱形变形频率,且对其他主要低阶振型频率影响较弱。文献[6]还研究了车窗高度、侧墙高度对模态频率的影响。总的来讲,结构修改会对车体质量、客室空间产生较大影响,而对模态频率的提高作用不大,因此有必要寻找其他简便且有益的措施。

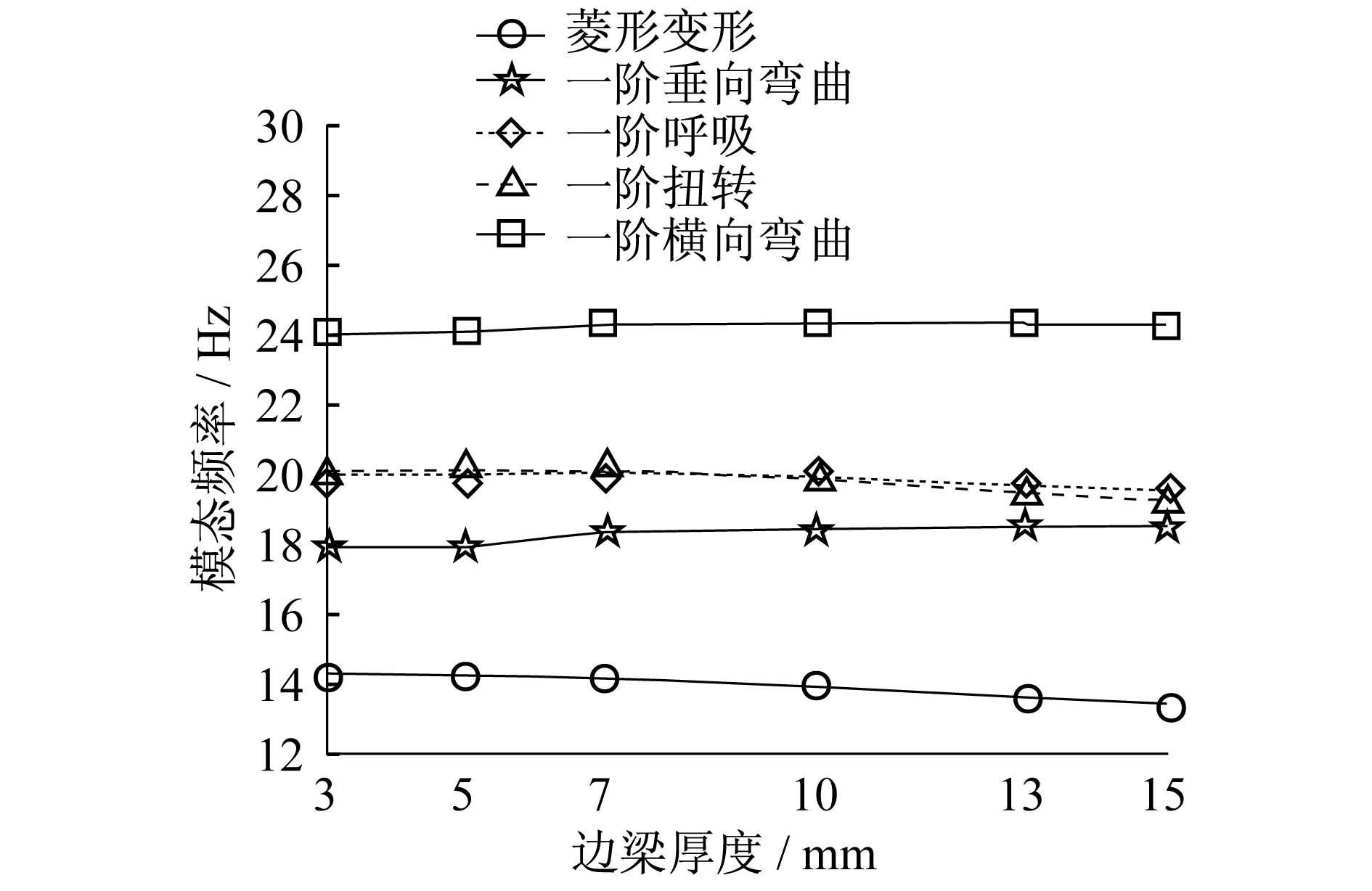
图1 承载结构边梁厚度对车体模态频率的影响

3 整备状态车体垂向弯曲频率分析

动力分散技术在高速铁路及城市轨道交通车辆中获得广泛运用。相比动力集中型列车,动力分散可以实现列车灵活编组、大功率牵引,以及充分利用轮轨粘着进而降低轮轨间动力作用的优势[7]。但动力分散意味着列车将采用更多的车下设备,导致造价和维护费用更高[8]。通常,车下设备按照吊挂方式可分为刚性吊挂与弹性吊挂。其中,刚性吊挂即直接将车下设备焊接或固接在车体下方；弹性吊挂则是采用隔振元件(如橡胶件等)将车下设备悬挂于客室下部。对于吊挂方案的选择,研究人员往往是从车体及设备振动的角度考虑,却并未分析车下设备吊挂方式对车体模态频率的影响。

3.1 整备状态车体模态频率简易计算及优化

由于车体整备状态下垂向一阶弯曲频率对车辆系统的振动影响最大,因此车体在整备状态下的垂向一阶弯曲频率是车辆设计及生产时重点关注的指标。整备状态下,由于内装、设备及附件的影响,车体模态频率计算工作量大,且计算精度不高,故目前主要通过试验方法获得。车体承载结构一般为金属结构,由于结构振动均考虑结构小位移线性行为,因此通过有限元分析技术即可获得承载结构较为准确的模态频率。研究表明,模态频率理论计算与试验结果的误差在5%以内[9]。误差主要由有限元建模时未计及的小附件、焊接附加质量、测试时支撑刚度影响和测试系统本身的误差造成。因此,可基于承载结构刚度不变原则,通过承载结构的垂向一阶弯曲频率来推算车体整备状态下的垂向一阶弯曲频率。

令fc为车体承载结构频率,fz为车体整备状态的垂向一阶弯曲频率,mc为车体承载结构质量,mz为整备状态下车体质量,则:

(1)

当推算出的fz低于预期数值时,因修改车体结构提高车体模态频率的难度相当高,可采用车下设备弹性悬置来提高fz。下吊设备弹性悬置是依据车体模态频率匹配准则和隔振设计的基本原理进行设计[5,10],一般来说,下吊设备的垂向自振频率选择在5～10 Hz。同样,依据承载结构刚度不变原则,设fzq为车体整备状态下期望的垂向一阶弯曲频率,那么至少需要的悬置设备质量Δm为:

(2)

如果已知现有车辆的fz、fzq,定义η=fzq/fz,则要提高现有车辆整备状态频率,悬置设备质量的最低值为:

Δmmin=mz(1-1/η2)

(3)

3.2 车体模态频率简易计算公式验证

为验证式(1)～(3)的正确性,采用图2所示包含下吊设备的整备状态车体有限元模型,分别采用有限元分析法和式(1)～(3)来分析刚性下吊、弹性下吊、弹性悬置质量对整备状态模态频率的影响。刚性吊挂元件采用多点约束(MPC)中的RBE 2单元。RBE 2是较常用的刚性单元,可将不同的单元焊接或铰接在一起。其主节点只需指定节点,不必指定自由度。因为主节点的6个自由度被用来参与对从节点的载荷分配或约束。本研究中刚性吊挂模型在各边梁的吊挂位置取一点做主动点,在设备相应位置取一点做从动点,选中该从动点的3个平动自由度,使其与主动点的6个自由度耦合。弹性吊挂元件采用有限元分析软件中的弹簧单元。

要建立如图2所示的有限元模型,需要掌握下吊安装位置,以及下吊设备的高度、体积、质心等参数。但在车辆设计之初,往往很难获得全面的参数。为了尽快获得车辆在整备状态下一阶垂向弯曲频率的估算,一个简单的办法是仅修改承载结构材料密度,使其质量与整备状态下车辆质量相同,然后对修改密度后采用有限元法计算的整备状态频率fzy与采用式(1)计算的理论值fzl进行对比。比较结果见表1。由于式(1)的前提条件是车体刚度保持不变,仅修改车体材料密度改变车体质量是最直观的方法。同时,因为车体结构和车体材料的弹性模量没有发生变化,也就是车体的刚度矩阵没有发生变化,因此此种情况时的验证是最准确的,且是最直观的。由表1可以看到,采用有限元承载结构密度修改法所计算出的整备状态频率与式(1)完全一致,此时可直接采用式(1)进行计算。

图2 整备状态车体有限元模型

mc/tfc/Hzmz/tfzl/Hzfzy/Hz9.74818.2730.010.4210.429.74818.2735.09.649.649.74818.2739.79.059.059.74818.2743.38.678.67

当下吊设备确定安装位置、形状、质心位置后,可以采用图2模型计算车体整备状态下的模态参数。本研究中,首先设置车下设备通过刚性连接(RBE 2单元)的方式将下吊设备吊挂在相应的位置,然后将车内座椅、装潢、通风道等其他设施通过调整车体材料密度,将这些质量均匀分布在车体上。对比分析结果见表2。

由表2可以看出,随着车体质量的增大,误差越来越小,且误差值均在5%范围内,说明采用刚性连接下吊时用式(1)进行频率估算有很高的准确性。

当采用刚性吊挂不能满足车体整备状态的频率要求时,往往需要设法修改车体整备状态的频率。整备状态的频率通过结构修改往往很难满足要求,采用弹性悬挂是一个有效的方法。以某型动车为计算对象,其整备质量为38.884 t,承载结构质量为9.748 t,承载结构一阶垂弯频率为18.27 Hz,选择不同的期望一阶垂弯频率,可根据式(2)求得悬置质量。采用式(2)计算悬置质量,并采用有限元模型进行计算的结果见表3。下吊设备弹性悬置模态频率分析结果如图3所示。依据文献[10]的分析,计算时悬置刚度选择为使设备吊挂后的静挠度为10 mm。

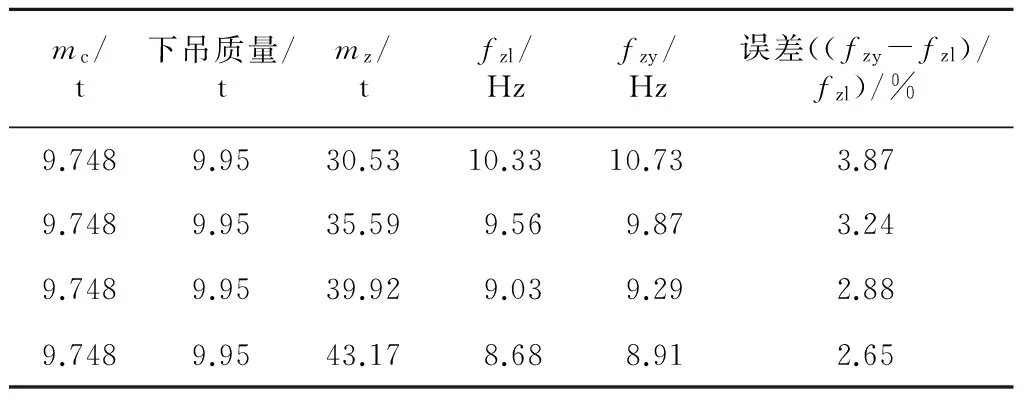
表2 下吊设备刚性吊挂时的分析结果对比

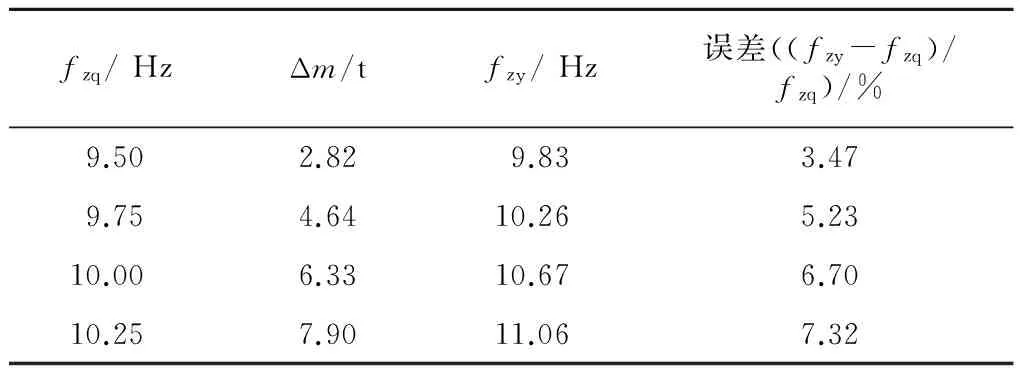
表3 式(2)计算结果验证

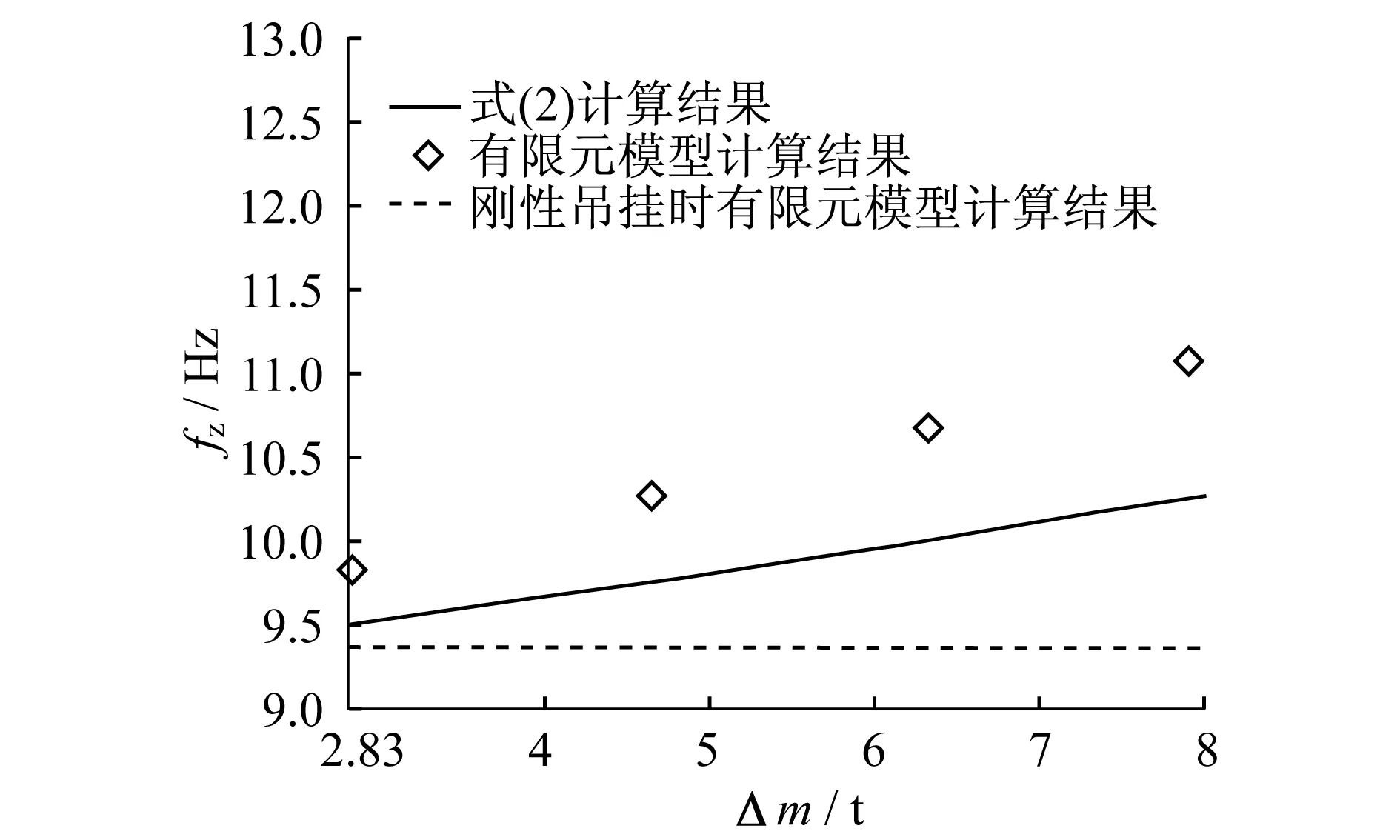
图3 下吊设备弹性悬置模态频率分析结果

从图3中可以看到,同样的悬置质量,有限元计算的频率要高于式(2)的估算频率；当悬置设备质量增加时,采用式(2)的计算误差增大。图4为弹性悬置质量与车体整备质量的关系,可以看到,车体整备质量越小,实现相同整备状态频率所需悬置的质量越小。

当计算或测出的车体整备状态的频率不满足要求时,可依据式(3)设置所需的悬置质量。表4及图5为采用式(3)和采用有限元模型的计算结果对比,所采用的模型和参数与验证式(2)时的一致。

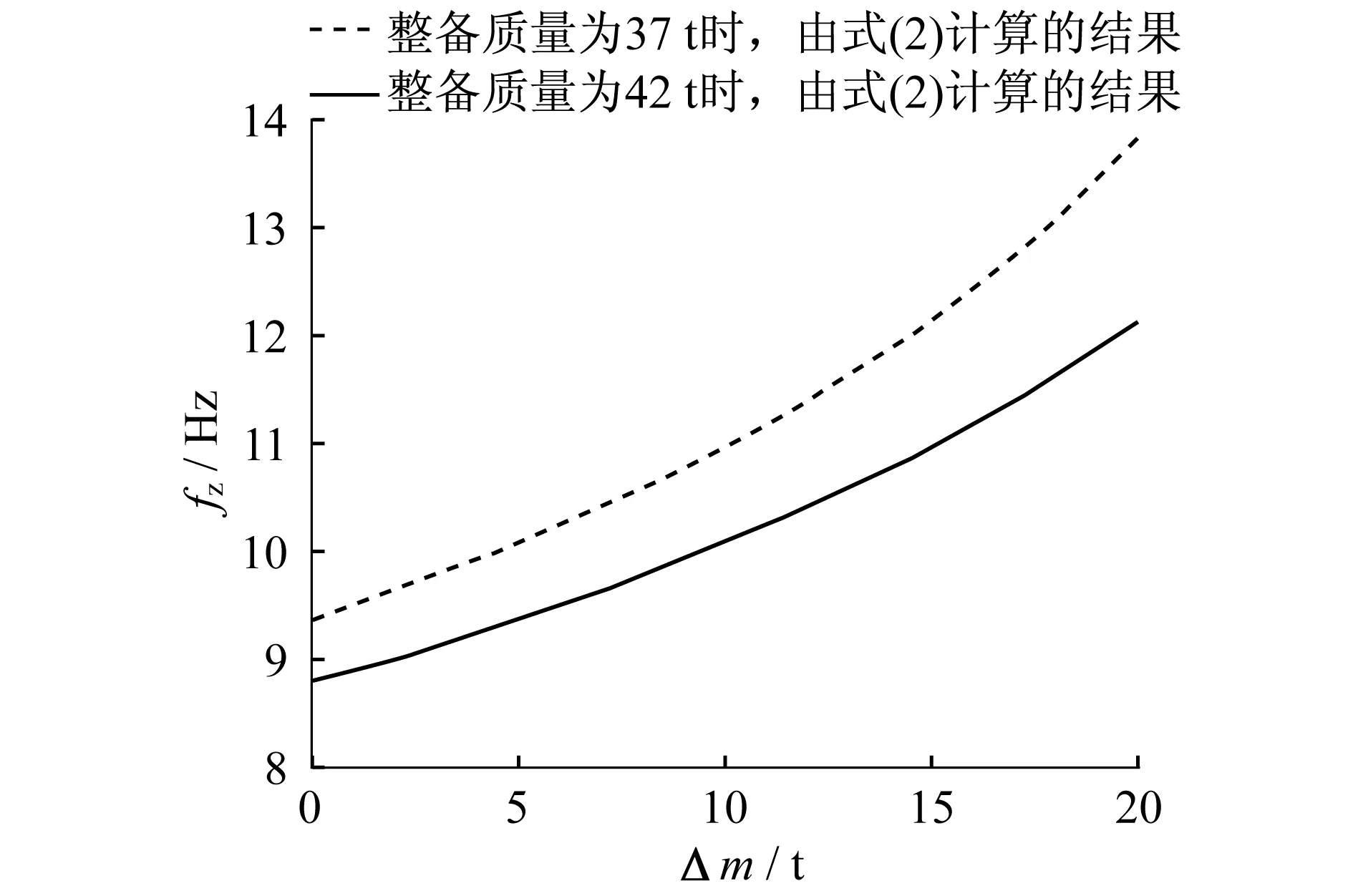
图4 弹性悬置质量与车体整备状态质量关系

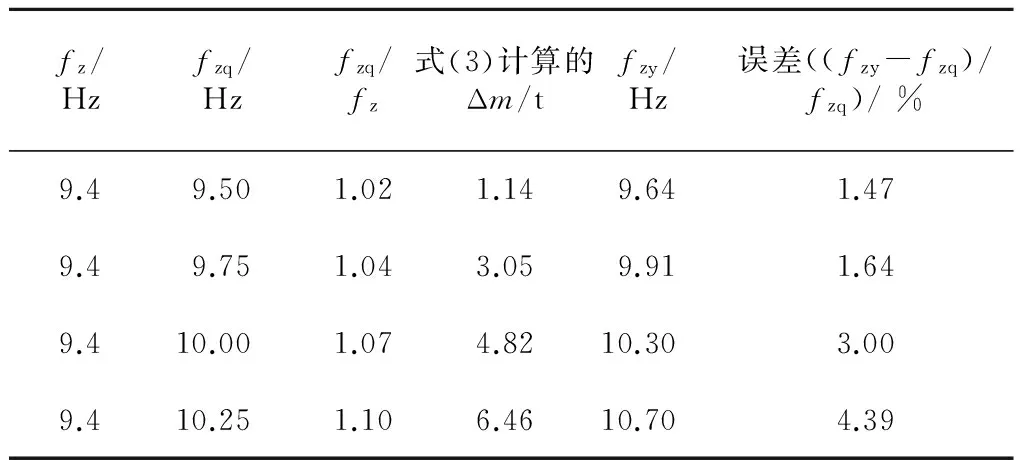
fz/Hzfzq/Hzfzq/fz式(3)计算的Δm/tfzy/Hz误差((fzy-fzq)/fzq)/%9.49.501.021.149.641.479.49.751.043.059.911.649.410.001.074.8210.303.009.410.251.106.4610.704.39

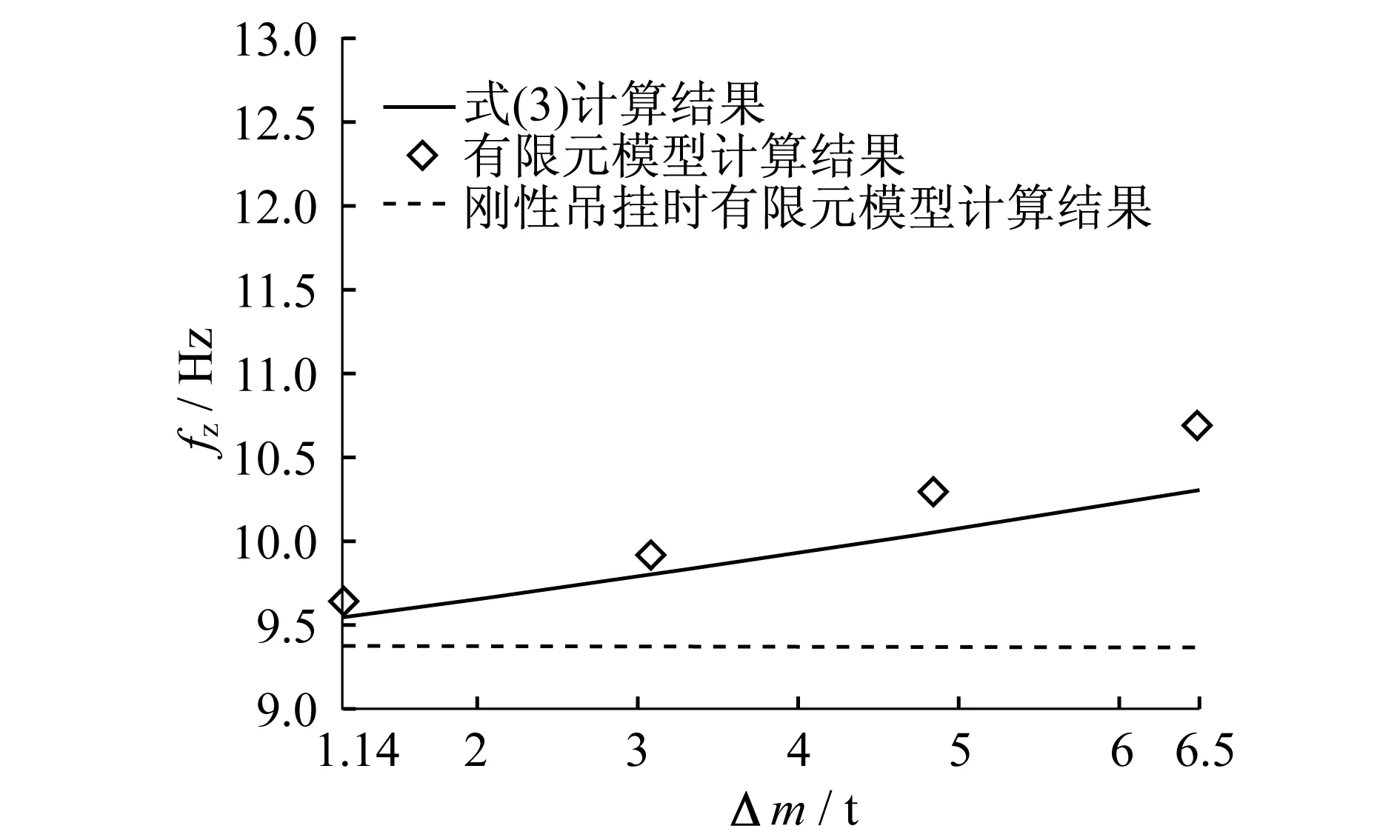
图5 悬置设备质量分析

从图5可以看到,当悬置设备质量在6.5 t以下时,计算误差在5%以下,说明式(3)计算结果有很高的准确性,且计算方法简单。实际计算分析时,可运用式(1)～(3)对模态频率、悬置设备质量进行估算后,再采用有限元进行细化分析。当已知车体的承载结构模态频率和悬置设备质量时,可运用式(2)估算出整备状态下的模态频率；在已知整备状态的测试频率与理论计算的整备状态频率比值后,可运用式(3)计算出该车的弹性悬置质量,这对掌握车辆结构、车辆二次结构的设计情况有理论和实际意义。

4 结语

为保证车辆具有良好的运行平稳性,车体垂向弯曲频率必须大于一定值,而仅对车体结构进行优化调整,无法达到大幅提升车体模态频率的目的。本文提出采用弹性吊挂提升车体弯曲频率的措施,并给出运用承载结构频率估算整备状态车体垂向弯曲频率和弹性悬置质量的公式。有限元分析表明,该公式具有相当精度,所提出的方法对整备状态的频率估算及提高整备状态的垂向弯曲频率具有指导意义。

[1] 周劲松.铁道车辆振动与控制[M].北京:中国铁道出版社,2012.

[2] ZHOU J,GOODALL R,REN L,et al.Influences of car body vertical flexibility on ride quality of passenger railway vehicles[J].Journal of Rail and Rapid Transit,2009,223(5):461.

[3] GONG D,ZHOU J,SUN W.On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber[J].Journal of Vibration and Control,2013,19(5):649.

[4] 周劲松,孙文静,宫岛.铁道车辆几何滤波现象及弹性车体共振分析[J].同济大学学报(自然科学版),2009,37(12):1653.

[5] 宫岛.高速列车车体弹性振动控制研究[D].上海:同济大学,2012.

[6] 张伟.车下设备对高速列车运行性能影响研究[D].上海:同济大学,2011

[7] 徐国梁.动力分散电动车组的发展[J].中国铁路,2002(2):57.

[8] 李春阳.高速电动车组的发展及其在我国的应用探讨[J].机车电传动,2003(5):15.

[9] 易鹏.A型地铁车体铝合金结构设计研究[D].上海:同济大学,2010.

[10] 宫岛,周劲松,孙文静,等.下吊设备对高速列车弹性车体垂向运行平稳性影响[J].中国工程机械学报,2011,9(4):404.

[11] 马敏纳,周劲松,赵阳阳.基于系统模态匹配策略的地铁车辆车体减振设计[J].城市轨道交通研究,2015(1):96.

On the Optimization ofRail Transit Carbody Bending Frequencies

WANG Yujie

Applying light structure of carbody is an effective way to reduce energy consumption and dynamic forces between rail and wheel. But light structure will directly reduce the modal frequency of carbody and thus increases the possibile risk of resonant vibration. Many researches have proved that it is not effective to increase the modal frequency of a fully-equipped carbody only by improving the overall structure. It is suggested that the bending frequency could be increased markedly with the equipment elastically suspended under carbody chassis, equations are given to evaluate the bending frequency of a fully-equipped carbody and the required mass of elastically suspended equipment. The correctness of the equations are validated with FEA method, which shows that the equations have relatively high precision and are significant in the evaluation of bending frequencies of fully-equipped carbody.

rail transit vehicle; carbody; modal frequency in fully-equipped condition

U 270

10.16037/j.1007-869x.2016.04.015

2015-05-17)