基于拓扑改变的地铁网络承载能力优化方法
孙 磊 李 荣 陈孝国
(1.浙江建设职业技术学院经济管理系,311231,杭州; 2.浙江商业职业技术学院财金学院,310053,杭州;3.黑龙江科技大学理学院,150022,哈尔滨∥第一作者,讲师)
基于拓扑改变的地铁网络承载能力优化方法
孙 磊1李 荣2陈孝国3
(1.浙江建设职业技术学院经济管理系,311231,杭州; 2.浙江商业职业技术学院财金学院,310053,杭州;3.黑龙江科技大学理学院,150022,哈尔滨∥第一作者,讲师)
基于复杂网络理论,提出一种利用拓扑结构改变策略来提高地铁网络承载能力的方法。首先,确定地铁网络的最大介数站点;其次,使得通过该站点的某条地铁线路在该站点越站运行;最后,以北京地铁网络进行仿真试验。结果表明:该策略下北京地铁网络最大介数站点的介数值大幅下降,各站点的介数分布得到优化。该方法有效提高了地铁网络的承载能力,但由于负荷的重新配置,有些地铁线路会出现客流量激增现象,需提早做好应对措施。
地铁网络; 承载能力; 拓扑结构改变策略
First-author′s address Department of Economic Management, Zhejiang College of Construction Technology, 311231,Hangzhou,China
复杂网络是研究复杂系统拓扑结构和行为的关键因素。小世界网络模型[1]与无标度网络模型[2-3]的提出在全球范围内引发了复杂网络研究的浪潮。起初的研究主要集中在网络的拓扑结构上,随着研究的深入,人们开始关注网络上的动力学过程,输运模型(Traffic Routing Model)[4-5]的研究受到极大的关注。以往关于输运模型的研究,主要针对网络承载能力(即单位时间内网络所能承受的最大进入负荷数,超过这一值,网络就会出现拥堵状态)。并提出许多提高承载能力的方法。
关于网络承载能力的决定因素研究,文献[4]提出了承载能力的推导公式:
(1)
式中:
D——该网络的平均最短路径;
Lmax——最大介数节点的编号;
Rc——网络的相变临界负荷个数;
BLmax——最大介数节点的介数值;
CLmax——最大介数节点的处理能力;
Bj——节点j的介数。
式(1)表明,在各节点处理能力(即节点能允许同时通过的最大负荷数)C相同的前提下,Rc受最大介数节点的制约,与最大介数节点的介数值成反比。因此,在其他条件不变的前提下,降低最大介数节点的介数值,可有效提高网络的承载能力。这也是本文研究的出发点。
提高网络承载能力的方法主要包括负荷行走路径改变策略和拓扑结构改变策略两种。实质就是通过策略实施,使得部分负荷运动绕过网络最大介数节点,从而有效降低最大介数节点的介数值,进而提高网络的承载能力。文献[6-7]提出通过改变负荷的行走策略从而有效提高网络的承载能力。文献[8]证明均匀网络由于缺少高介数节点而表现出更大的网络承载能力。文献[9]指出点或边的移除能够减轻甚至缓和网络上由于过载造成的故障。文献[10]提出了拓扑结构改变策略,通过增加或减少一些边来改变网络结构,从而提高网络的承载能力;指出增加点或边的成本较大,最简单且成本最低的策略就是删除点或边,并提出HDF(High-Degree-First)策略。首先根据km×kn的乘积排序,其中km、kn是边的两端节点的度;然后根据排序,从大到小依次关闭对应的边。因为HUB节点(网络中连接数非常大的节点)非常重要,且承载非常多的负荷,km×kn越大则对应的边越容易拥堵。所以,移除它会导致负荷的重新分流,进而增强网络的处理和运输能力。结果显示,根据km×kn来关闭某些边可以显著提高网络的承载能力。文献[11]提出HBF(High-Between-First)策略,其将HDF策略稍加改变,采用介数来代替度。仿真结果显示,HBF策略的效果好于HDF策略。文献[12]提出VNDR(Variance-of-Neighbor-Degree-Reduction)策略,该策略不仅考虑到HUB节点的重要性,还通过降低某些节点的邻居节点之间的度差异性来平衡这些节点到邻居节点的负荷数量。仿真结果表明,该策略的效果要好于HBF策略,但复杂程度较高。
近年来利用复杂网络理论进行交通网络的研究越来越受到关注。文献[13]运用复杂网络理论对上海轨道交通近期(2012年)规划网络拓扑结构进行了分析。文献[14]设计了轨道交通运营网络的连通可靠性仿真分析的新算法,并应用到上海轨道交通遭受攻击后的连通性分析上。在交通网络中通过网络拓扑结构改变策略来提升交通能力的研究也被经常报道。在高速公路网络中,为了缓解高峰期交通压力,往往关闭一些道路,而要实现道路的关闭,交管部门只需要关闭这些道路的入口。随着社会的快速发展,交通网络的规模越来越大,这带给交通管理部门新的挑战。考虑到增加点和边所带来的成本,交通管理部门在交通规划时必须小心谨慎,因为不正当的加入点和边,不但不能缓解交通反而会恶化交通。例如,2003年12月29日,连接上海交通大学徐汇校区和闵行校区的沪闵高架路正式开通,很多原来走不同道路的司机在当天早上都选择沪闵高架,致使车辆过多造成严重拥堵。
地铁网络不同于一般的交通网络。在一般的交通网络中关闭某一条边,不影响交通网络的正常运行。地铁列车只能在规定的线路上运行,不能关闭地铁线路中的某段线路,否则该线路无法正常运行。基于此,本文提出一种适合地铁网络的拓扑结构优化策略,通过降低最大介数节点的介数值,从而有效提高地铁网络的承载能力。同时还关注到不同策略实施对地铁网络造成的后续影响。
1 基础知识
1.1 输运模型
为了模拟现实网络,引入输运模型。考虑到网络的拓扑结构及网络上的负荷运动,做以下假设:
首先,每时每刻进入网络的负荷数为R,这些负荷的起点和终点随机在网络上产生,负荷按照最短路径行进(当起点和终点之间存在多条最短路径时,随机选取一条);每时每刻也有负荷到达目的地,而在下一时刻从网络中消失。
其次,网络中每个节点都有一定的负荷处理能力C,本文实证分析中设地铁网络各站点C=10。当通过某节点的负荷超过其处理能力时,会产生局部拥堵,导致网络上的负荷集聚,进而增大负荷到达目的地的难度。
第三,在网络中每个负荷都有它的目的地,即使在出现拥堵的情况下,也不会改变自己的行进路线,只会延长通过拥堵节点的等待时间。此外,负荷通过节点时按照到达该节点的时间顺序“先进先出”。
1.2 节点介数的定义
在使用最短路径路由算法的网络中,节点介数指标刻画负荷经过给定节点的可能性。节点介数值大,节点在网络中就居于核心地位。具体定义如下:
(2)
式中:
ghk——节点h和节点k之间的最短路径数;
ghk(j)——节点h和节点k之间经过j的最短路径数;
(N-1)(N-2)/2——最大可能的点介数。
2 地铁网络拓扑结构优化策略
考虑到地铁网络的实际情况,做以下几点假设:① 人是理性的,人在既定的条件下,在起点和目的地之间总会选择最短路径策略;② 对于地铁网络,线路是固定的,若起点和目的地不在同一条线路上,负荷需要通过换乘站点换乘才能到达目的地,为方便研究,换乘成本忽略不计。以北京地铁网络西直门站点为例介绍拓扑结构优化策略(以下简为“TC策略”)的实现过程。西直门站点处于2号线和4号线的交汇处,两种TC策略如下:
(1) TC 1策略:2号线在西直门站越站运行。对应到地铁网络拓扑结构上,42站点(西直门站)、41站点(积水潭站)和43站点(车公庄站)的边删除,直接在41站(积水潭站)和43站(车公庄站)之间连边,如图1所示。
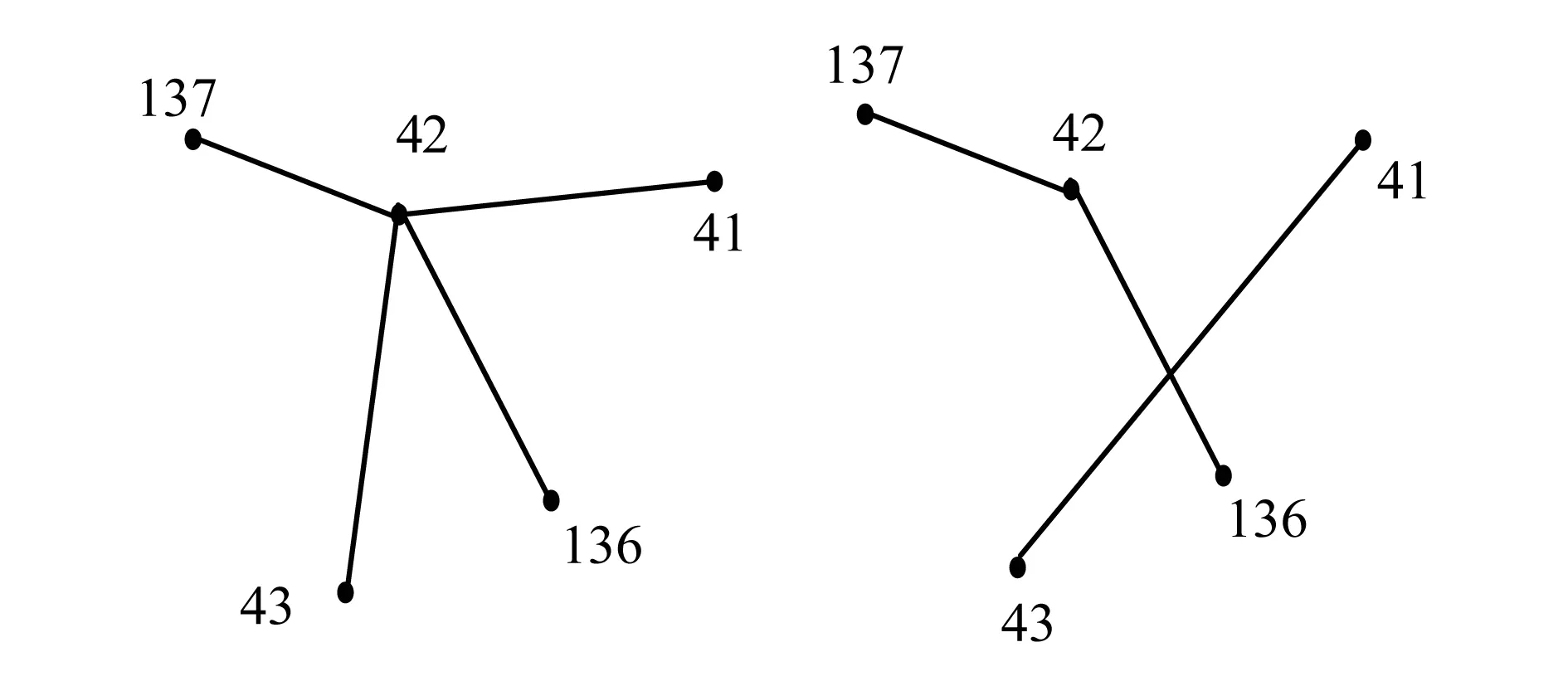
图1 2号线在42站点越站运行前后的拓扑结构
(2) TC 2策略:4号线在西直门站点越站运行。对应到地铁网络拓扑结构上,42站点(西直门站)、136站点(新街口站)和137站点(动物园站)的边删除,直接在136站点(新街口站)和137站点(动物园站)之间连边,如图2所示。

图2 4号线在42站点越站运行前后的拓扑结构
3 试验数据对比
3.1 2004—2013年北京地铁网络的发展变化
从客运量来看,2004年北京地铁年客运量达到6.066 8亿人次,创历史新高,比2003年增长28.57%;2013年北京地铁年客运量达32.09亿人次,比2012年增长28.7%,比2004年增长4.29倍。从运营线路长度来看,2004年底北京地铁的运营线路为4条,长度为114 km;2013年底,北京地铁共有17条运营线路,长度达465 km。2013年底北京地铁运营线路如图3所示。表1为北京地铁拓扑结构网络中介数排名前10位的站点,其中的数据通过MATLAB软件和PAJEK软件[15]计算所得。
图3 2013年北京地铁运行网络图
3.2 基于HBF策略的北京地铁网络各站点介数变化情况
从表1可以看出,42(西直门站)和43(车公庄站)站点的介数值排名居前两位。删除这两个站点之间的边,观察删除后地铁网络各站点介数的变化情况。考虑到HBF策略不适用于地铁网络,这里只进行方法上的对比。具体数据如表2所示。
表2显示:HBF策略下,地铁网络的最大介数节点仍是42(西直门站)站点,其介数值从0.266 9下降到0.235 9,降幅达12%。网络承载能力有所提升,从最初的35上升到40。而43(车公庄站)站点的介数值从0.211 5下降到0.078 4,降幅高达63%。
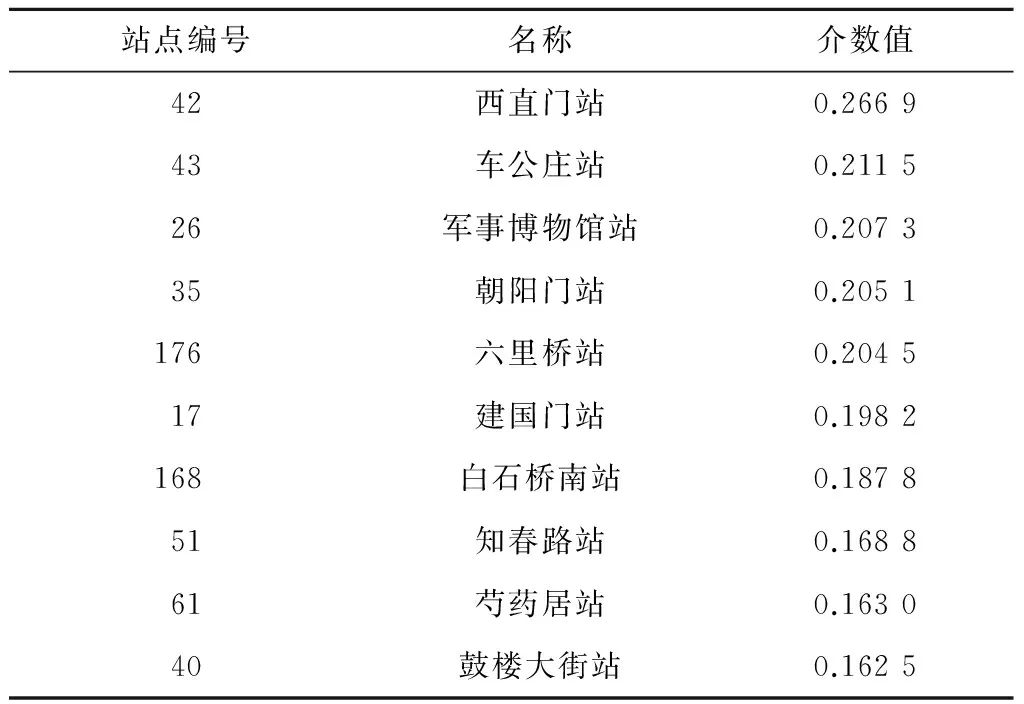
表1 介数值排名前10位的站点
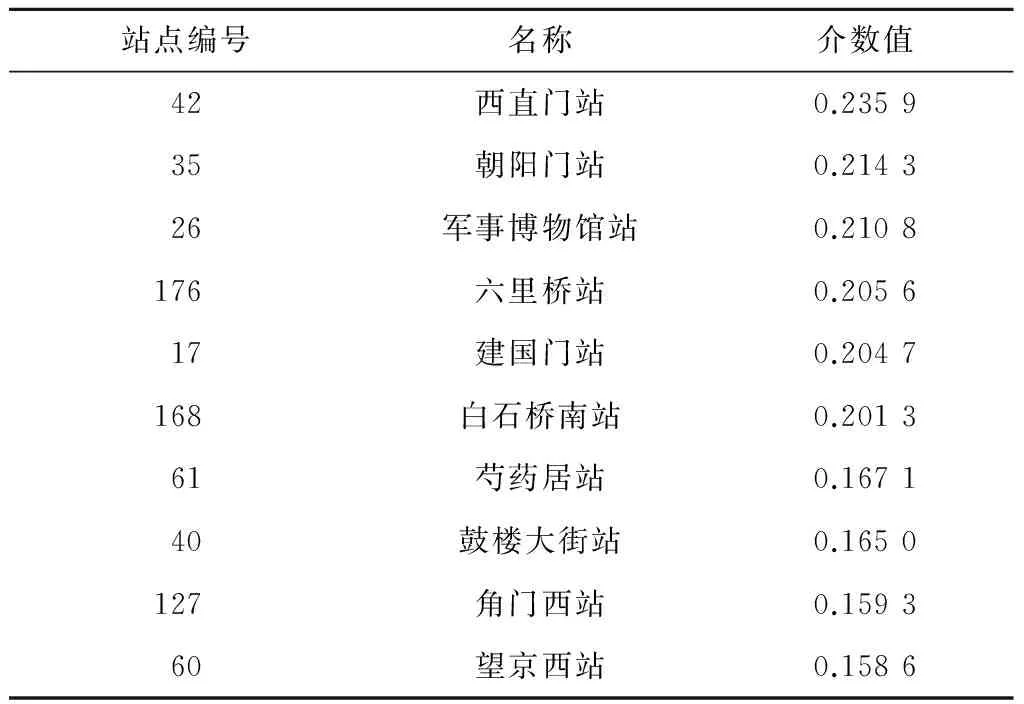
表2 HBF策略下介数值排名前10位的站点
3.3 基于TC策略的北京地铁网络各站点介数变化情况
3.3.1 TC策略下介数值排名前10位的站点
基于上述两种TC策略的地铁网络各站点介数变化情况如表3和表4所示。
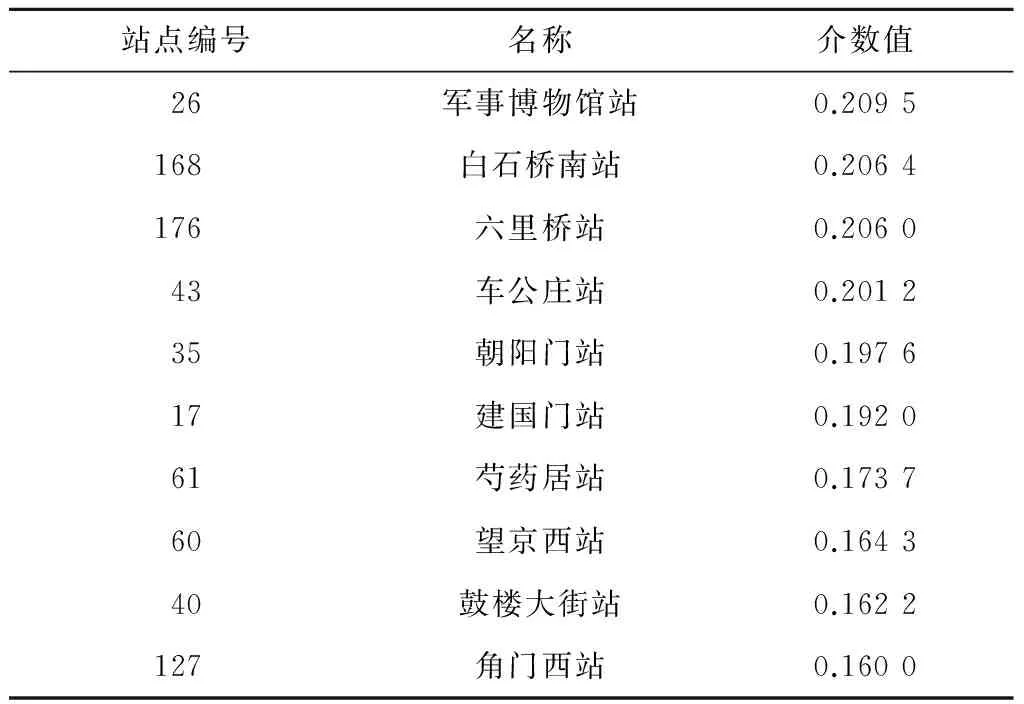
表3 TC 1策略下介数值排名前10位的站点
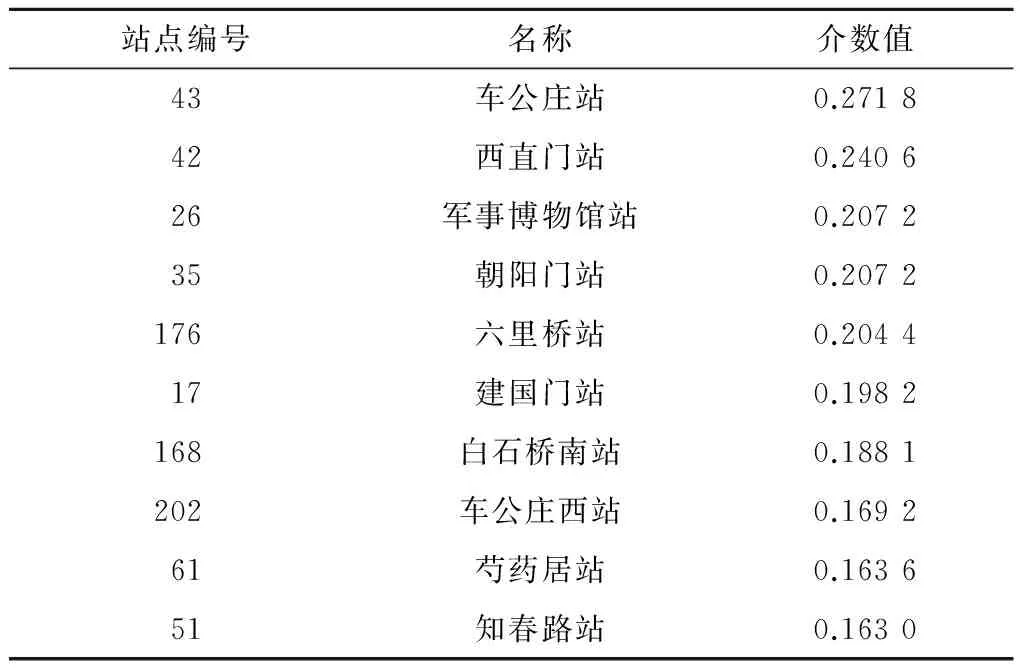
表4 TC 2策略下介数值排名前10位的站点
由表3可以看出,TC 1策略实施后,可以将网络的最大介数节点的介数值从42站点(西直门站)的0.266 9降为26站点(军事博物馆站)的0.209 5,降幅达22%。网络承载能力从最初的35大幅上升到45。而42站点(西直门站)的介数值大幅下降到0.124 8,降幅达53%。
由表4可以看出,TC 2策略实施后,网络的最大介数节点的介数值从42站点(西直门站)的0.266 9小幅上升为43站点(车公庄站)的0.271 8。网络承载能力从最初的35小幅下降到34。而42站点(西直门站)的介数值下降到0.240 6,降幅为10%。
3.3.2 TC策略下介数值增幅排名前5位的站点
TC策略下地铁网络各站点介数值增幅排名前5位的站点如表5和表6所示。
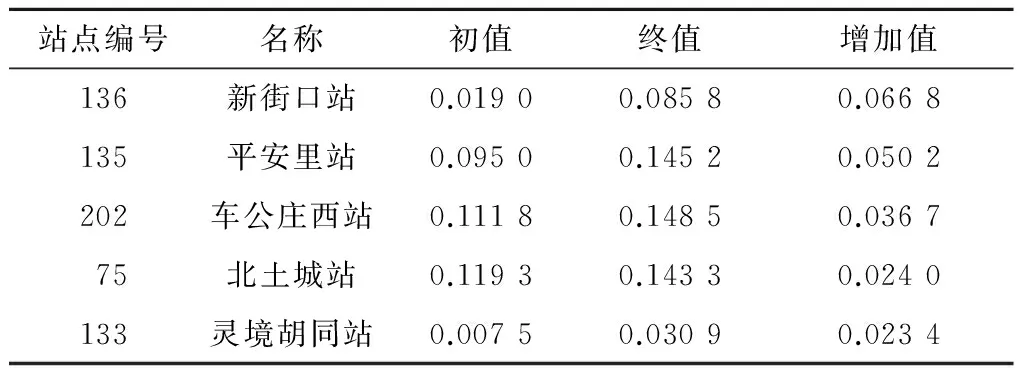
表5 TC 1策略下介数值增幅前5位的站点
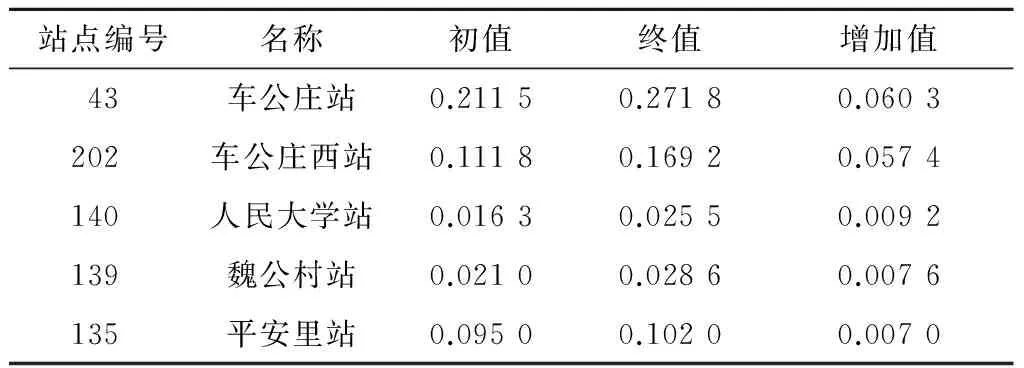
表6 TC 2策略下介数值增幅前5位的站点
从表5中可以看出,TC 1策略实施后,136(新街口站)和135(平安里站)站点的介数值大幅增加,尤其是136(新街口站)站点,介数值从0.019 0大幅上升到0.085 8。
从表6中可以看出,TC 2策略实施后,43(车公庄站)和202(车公庄西站)站点的介数值大幅增加,均超过0.05。
4 结语
以往的研究表明,网络的承载能力受最大介数节点的制约,降低网络最大介数节点的介数值,等价于提高网络的承载能力。基于此,考虑到地铁网络的实际特点,本文提出TC策略来有效降低地铁网络站点的最大介数值,达到提高网络承载能力的目的,并以北京地铁网络为底层拓扑结构,实证分析各种拓扑结构改变策略的具体做法,以及对网络各站点介数的影响。结果显示:
(1) TC策略对改善北京地铁网络的承载能力效果显著。不同的拓扑结构改变策略对网络承载能力的影响大不一样。TC 1策略的效果最显著,其将地铁网络最大介数节点的介数值从0.266 9降为0.209 5,下降幅度高达22%,从而有效提高网络的承载能力,而42(西直门站)站点的最大介数节点地位由26(军事博物馆站)站点取代;TC 2策略实施后,网络的最大介数节点的介数值从42站点(西直门站)的0.266 9小幅上升为43站点(车公庄站)的0.2718,网络的承载能力反而小幅下降;HBF策略下,地铁网络的最大介数节点仍是42(西直门站)站点,介数值从0.266 9下降到0.235 9,下降幅度为12%,网络的承载能力有所提升。
(2) TC策略实施对地铁网络的后续影响不容忽视。改变网络拓扑结构,使得负荷绕开HUB节点,负荷分配更加均匀,从而有效提高网络承载能力。不同的策略实施后,会导致不同的负荷分配,例如,TC 1策略实施后,136(新街口站)和135(平安里站)站点的介数值大幅增加,由于这两个站点均在4号线上,预示着2号线在42(西直门站)站点越站运行后,会有更多的客流选择4号线;TC 2策略实施后,43(车公庄站)和202(车公庄西站)站点的介数值大幅增加,预示着4号线在42(西直门站)站点越站运行后,会有更多的客流选择6号线。
[1] WATTS D J,STROGATZ S H.Collective dynamics of small world networks[J].Nature,1998,393:440.
[3] ALBERT R,BARABSI A L.Statistical mechanics of complex networks[J].Rev of Modern Phys,2002,74:47.
[4] ZHAO L,LAI Y C,PARK K,et al.Onset of traffic congestion in complex networks[J].Physical Review E,2005,71(2):026125.
[6] WANG W X,WANG B H,YIN C Y,et al.Traffic dynamics based on local routing protocol on a scale-free network[J].Physical Review E,2006,73(2):026111.
[7] WANG W X,YIN C Y,YAN G,et al.Integrating local static and dynamic information for routing traffic[J].Physical Review E,2006,74(1):016101.
[8] GUIMERA R,ARENAS A,DAZ-GUILERA A,et al.Dynamical properties of model communication networks[J].Physical Review E,2002,66(2):026704.
[9] MOTTER A E.Cascade control and defense in complex networks[J].Physical Review Letters,2004,93(9):098701.
[10] LIU Z,HU M B,JIANG R,et al.Method to enhance traffic capacity for scale-free networks[J].Physical Review E,2007,76(3):037101.
[11] ZHANG G Q,WANG D,LI G J.Enhancing the transmission efficiency by edge deletion in scale-free networks[J].Physical Review E,2007,76(1):017101.
[12] HUANG W,CHOW T W S.An efficient strategy for enhancing traffic capacity by removing links in scale-free networks[J].Journal of Statistical Mechanics:Theory and Experiment,2010,2010(1):P01016.
[13] 王燚,杨超.上海市轨道交通网络的复杂网络特性研究[J].城市轨道交通研究,2009(2):33.
[14] 丁小兵.复杂网络理论及其在上海城市轨道交通网络可靠性分析评价中的应用[J].城市轨道交通研究,2012(11):50.
[15] De NOOY W,MRVAR A,BATAGELJ V.Exploratory social network analysis with Pajek[M].Cambridge:Cambridge University Press,2011.
Subway Network Capacity Improvement Based on Topology Change
SUN Lei, LI Rong, CHEN Xiaoguo
Based on complex network theory, an approach to improve the capacity of subway network by usingthe strategy of topological structure change is proposed. Firstly, the site with the largest betweenness is determined; secondly, a subway line passing through this site is arranged to overtake the station; and finally, Beijing subway network is taken for simulation. Results show that the largest betweenness value of Beijing subway network is reduced dramatically under this strategy, and the betweenness distribution of all the sites is optimized. This method can improve the capacity of Beijing subway network, but due to the re-assignment of transport loads, surges in passenger traffic on some lines will certain happen, so necessary measures should be taken as early as possible.
subway network; network capacity; strategy of topological structure change
U292.5∶U231
10.16037/j.1007-869x.2016.04.001
2014-04-30)

