利用向量的内积证明几何题
买买吐送·尼扎木丁
(和田师范专科学校数信学院, 新疆 和田 848000)
利用向量的内积证明几何题
买买吐送·尼扎木丁
(和田师范专科学校数信学院, 新疆 和田 848000)
本文介绍了利用向量的内积证明几何题的方法,是证明几何题的另一种方法。
向量的内积;证明几何题;数学证明方法
向量是数学中的重要概念之一,它广泛应用于生产实践和科学研究中,向量在解决初等几何问题,立体几何问题,解析几何问题中广泛应用。向量的内积也广泛应用,利用向量的内积容易证明初等几何问题,立体几何问题和解析几何问题。利用内积证明几何问题时,可以减少辅助线的添加,还可以避开一些较复杂的空间图形,降低了证题的难度且思路明确,易于下手,易于接受。下面看几个问题.
例1,证明四面体对棱夹角公式.
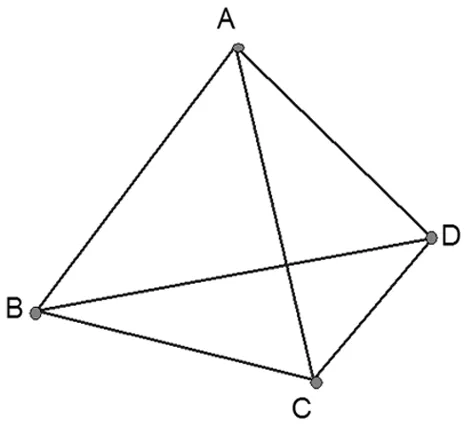
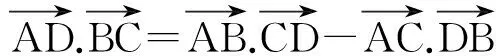

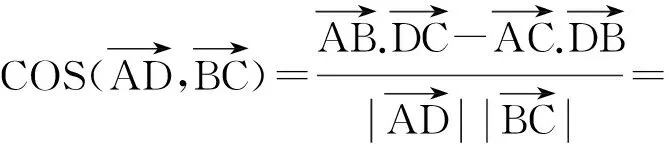

例2,如图所示,直线l与平面α内的三条共点直线所成的角相等,则求正:l⊥α


由已知得

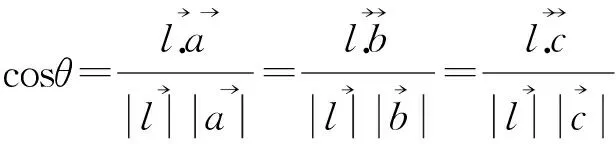
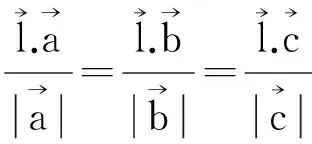


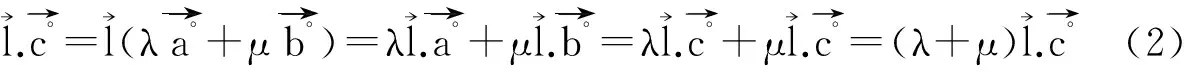


例3,如图,已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直,M,N分别为对角线AE和BE上的点且AM=DN,求证:MN∥平面BCE。
过点N作NN1⊥BC,NN2⊥AB,垂足分别是N1,N2.
设NN1=x,NN2=y,则x=y,所以N(x,x,0).
同理,过N作MM1⊥BE,MM2⊥AB,垂足分别为M1,M2.
设MM1=x,MM2=z,则z=a-x,(AB=a).
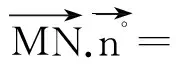


例4,如图所示,已知直三棱柱A1B1C1-ABC中,A1C1=B1C1,AC1⊥A1B,M,N分别是A1B1,AB的中点,求证:AB⊥BC.
设A(-a,0,0),B(a,0,0),C(0,c,0),A1(-a,0,h),C1(0,c,h),B1(a,0,h),则
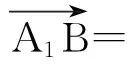



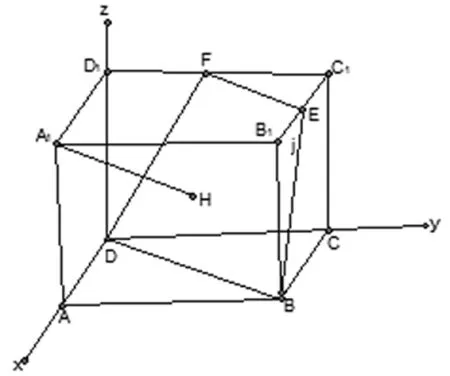
例5,已知棱长为1的正方体ABCD-A1B1C1D1,E,F是棱B1C1和C1D1的中点,求证点A1到平面BDFE的距离等于1。
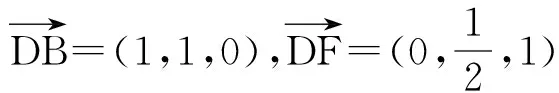
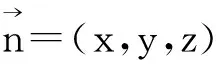



所以点A1到平面BDFE的距离等于1.
证明几何题时,有时利用向量的内积避免了作太多的辅助线,可以节约时间,避免一些不必要的麻烦,更容易得到证明。
2016-08-10
买买吐送·尼扎木丁(1964-),男,维吾尔族,和田师范专科学校数信学院副教授。研究方向:几何学。

