新型双模光子晶体光纤的平坦色散特性分析

杨 静,施伟华

(南京邮电大学光电工程学院,南京 210003)

新型双模光子晶体光纤的平坦色散特性分析

杨 静,施伟华

(南京邮电大学光电工程学院,南京 210003)

设计了一种具有色散平坦特性的双模PCF(光子晶体光纤),采用全矢量FEM(有限元法)计算了光纤的模式及色散特性,分析了光纤结构对色散平坦性的影响。结果表明,当PCF的孔间距Λ=10μm,相对孔径d1/Λ=0.55、d2/Λ=0.65和d3/Λ=0.75时,基模和二阶模的限制损耗均小于1 dB/m,两种模式的有效折射率差值Δneff＞10―3,实现了稳定的双模传输。在C波段,色散斜率介于―0.012 36～0.321 91 ps/(nm2·km)之间,波长1 550 nm处,基模和二阶模的色散斜率分别为0.093 80和0.038 97 ps/(nm2·km),实现了C波段的平坦色散。

少模光纤;光子晶体光纤;有限元法;色散

0 引 言

WDM(波分复用)是扩充光网络传输系统通信容量的主要技术,但以单模光纤为主要传输媒介的WDM系统的非线性容忍度小,使得其传输容量越来越接近香农极限[1]。为了减小光纤的非线性,克服光纤通信的容量限制,引入了基于少模光纤的MDM(模分复用)技术[2]。

PCF(光子晶体光纤)因其独特的光学特性和灵活的结构设计,为少模光纤的设计提供了新的思路。2012年,Takayoshi Mori[3]等通过优化结构,实现了多种模式传输的少模PCF,但在工作区域存在严重的模式串扰,存在模式不稳定的问题。另外,色散作为通信光纤的重要性能指标[4],在少模PCF中鲜有研究。因此,如何获得稳定的低损耗模式传输及平坦的色散特性是设计少模PCF的关键。

本文设计了一种双模PCF,通过合理地控制光纤结构参数,实现了稳定的双模传输,通过全矢量FEM(有限元法)研究了双模PCF的限制损耗、有效模场面积和色散特性,并分析了PCF结构参数对色散特性的影响,从而进一步优化光纤。

图1 双模PCF的横截面结构

1 光纤的设计

本文设计的双模PCF的横截面结构如图1所示。其包层由3层三角晶格排列的空气孔组成,孔间距设为Λ。通过逐层改变空气孔的直径,可以获取更为平坦的色散曲线[5]。基底材料SiO2的

折射率可通过Sellmeier[6]方程计算,在1 550 nm工作波长下,基底折射率为1.444。该PCF从内至外3种空气孔的孔径分别为d1、d2和d3,相对孔径定义为d1/Λ、d2/Λ和d3/Λ。根据ITU-T光纤标准,取光纤直径为125μm。

2 稳定的双模特性

2.1 模式计算结果

利用全矢量FEM并采用COMSOL Multiphysics软件,结合各向异性的PML(完美匹配层)边界条件,对双模PCF中各模式的有效折射率及模场分布进行数值模拟。取结构参数为Λ=10μm、d1/Λ=0.55、d2/Λ=0.60和d3/Λ=0.65,得到1 550 nm波长处各传输模式的模场分布如图2所示。根据线偏振模与矢量模之间的对应关系,LP1n模由一个HE2n和TE0n以及TM0n叠加而成。因此二阶模又可表示为LP11。

图2 双模PCF各模式的模场及电场矢量分布

2.2 限制损耗

对于石英PCF,其限制损耗Lc为

式中,k0=λ/2π为真空自由波数,λ为自由波长;neff为模式的有效折射率。根据光纤中模式传输理论,当传输模式的限制损耗大于1 dB/m时,该模式截止[7]。图3所示为S-C波段上各模式的限制损耗图。

图3 双模PCF各模式在S-C波段上的限制损耗

2.3 模间串扰分析

对于单芯少模PCF,需要考虑传输模式间的相互串扰问题,一般定义当同一纤芯中两个模式的有效折射率差值大于0.001时,两种模式间的串扰可忽略[8]。图4所示为S-C波段双模PCF各模式间的有效折射率neff及有效折射率差Δneff与波长的关系曲线。

图4 双模PCF各模式的有效折射率及模式间有效折射率差与波长的关系曲线

由图4可知,LP01和LP11的正交偏振态属于良好的简并态,且各传输模限制损耗均小于1 d B/m。两个模式的Δneff＞0.001时,说明很好地抑制了两种模式间的串扰。综上所述,该双模PCF实现了稳定的双模传输。

3 光纤的色散特性

相比于传统光纤,PCF可以灵活地将光纤的零色散点调至所需的波长,并实现大波长范围内的平坦色散。PCF的总色散近似为材料色散Dm和波导色散Dw之和,即

其中,波导色散的计算公式如下:

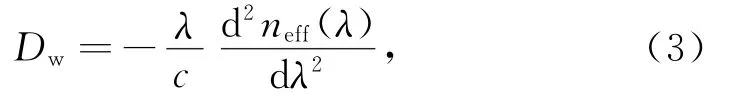
式中,c为光速。对石英PCF而言,材料色散是确定的,可由Sellmeier方程计算,因此波导色散决定了总色散。波导色散与PCF的结构和折射率分布有关,合理地调整PCF的空气孔大小和空气孔排列方式等结构参数,可以使光纤的波导色散与材料色散在一定波长范围内相互抵消[9],获得平坦的色散曲线。本文重点研究C波段光纤基模和二阶模的色散特性。

3.1 不同Λ对双模PCF色散特性的影响

图5所示为d1/Λ=0.50、d2/Λ=0.60和d3/Λ=0.65时,不同Λ下两种模式的色散随波长的变化情况。由图可知,当Λ增大时,色散系数也随之增大,但色散曲线的平坦度没有明显变化,说明Λ主要对色散曲线的走向起作用,对平坦度的影响较小。

图5 空气孔间距Λ对光纤色散曲线的影响

当Λ=10μm时,基模和二阶模在C波段的相对色散系数Dmax―Dmin分别为2.138 41和1.154 09 ps/(nm·km),均小于5 ps/(nm·km),满足色散平坦的要求[10]。比较两种模式的色散曲线发现,二阶模的色散平坦性更优,这是由于二阶模的部分能量会分散在包层中传输,能量分布随波长变化较大,因而其总色散受波导色散的调节作用比较大,更易获得平坦的色散曲线。

3.2 包层空气孔孔径对双模PCF色散特性的影响

为了研究包层空气孔孔径对色散特性的影响,设定孔间距Λ=10μm不变,当相对孔径不同时色散随波长的变化如图6所示。从图中可以看出,当孔间距Λ相同时,逐层空气孔大小相差越大,基模和高阶模的色散曲线越平坦,在1 500～1 600 nm波长范围内,3种模式的色散曲线在d1/Λ=0.55、d2/Λ=0.65和d3/Λ=0.75时达到最佳平坦度。

3.3 色散斜率

为了更直观地表征光纤的色散特性,用色散斜率表示色散系数随波长的变化情况,色散斜率可表示为Dslope=d D/dλ,两种模式的色散斜率在C波段的变化曲线如图7所示。采用优化后的PCF结构参数:Λ=10μm,d1/Λ=0.55、d2/Λ=0.65、d3/Λ= 0.75。由图可知,在C波段,色散斜率介于―0.012 36～0.321 91 ps/(nm2·km)之间,在1 550 nm波长处,各模式的色散斜率分别为0.093 80和0.038 97 ps/(nm2·km),表现出了良好的色散平坦性。

图6 不同空气孔占空比对光纤色散曲线的影响

图7 在C波段各模式的色散斜率随波长的变化关系图

4 结束语

本文设计了一种双模PCF,采用优化后的PCF结构参数Λ=10μm、d1/Λ=0.55、d2/Λ=0.65、d3/Λ=0.75时,光纤中传输模式分别为基模LP01和二阶模LP11。研究了光纤的色散特性,发现在C波段波长1 550 nm处,模式的色散斜率分别为0.093 80和0.038 97 ps/(nm2·km),表现出了良好的色散平坦性。比较发现,二阶模的色散平坦性最好,验证了二阶模作为承载模式的可行性和优越性。本文的研究在MDM系统的中有着重要的应用前景。

[1]Ellis A D,Zhao J,Cotter D.Approaching the Non-Linear Shannon Limit[J].Lightwave Technology Journal of,2010,28(4):423―433.

[2]Erdague S,Facq P.Mode division multiplexing in optical fibers[J].Appl Opt,1982,21(11):1950―1955.

[3]Mori T,Sakamoto T,Wada M,et al.Few-mode photonic crystal fibre for wideband mode division multiplexing transmission[C]//2012 38th European Conference and Exhibition on Optical Communications.Amsterdam,Holland:IEEE,2012:1―3.

[4]Saitoh K,Koshiba M,Hasegawa T,et al.Chromatic dispersion control in photonic crystal fibers:application to ultra-flattened dispersion[J].Optics Express,2003,11(8):843―852.

[5]Wang J,Jiang C,Hu W,et al.Modified design of photonic crystal fibers with flattened dispersion[J]. Optics&Laser Technology,2006,38(3):169―172.

[6]Russell P S J.Photonic crystal fibers[J].Science,2003,299(5605):4729―4749.

[7]Haxha S,Ademgil H.Novel design of photonic crystal fibres with low confinement losses,nearly zero ultraflatted chromatic dispersion,negative chromatic dispersion and improved effective mode area[J].Optics Communications,2008,281(2):278―286.

[8]Saitoh K,Koshiba M.Empirical Relations for Simple Design of Photonic Crystal Fibers[J].Optics Express,2005,13(1):47―52.

[9]Ferrando A,Silvestre E,Andres P,et al.Designing the properties of dispersion-flattened photonic crystal fibers[J].Optics Express,2002,10(13):687―697.

[10]杨旺喜,周桂耀,夏长明,等.C波段具有平坦近零色散光子晶体光纤的一种改进设计方法[J].物理学报,2011,60(10):395―400.

Analysis of Flattened-Dispersion Characteristic of a New Type of Double-Mode Photonic Crystal Fiber

YANG Jing,SHI Wei-hua
(School of Optoelectronic Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

In this paper,a new type of double-mode photonic crystal fiber with flattened-dispersion is designed.The transmission and dispersion properties are simulated by Finite Element Method(FEM).The impacts of the parameters of the PCF on the dispersion properties are analyzed.The results show that the double-mode PCF can gain stable transmission of the two modes when the structural parameters of PCF areΛ=10μm,d1/Λ=0.55,d2/Λ=0.65,d3/Λ=0.75.The confinement loss of each mode is less than 1 dB/m,and the effective refractive index difference is larger than 10―3.The dispersion slope values ranges from―0.012 36 ps/(nm2·km)to 0.321 91 ps/(nm2·km)in the C band.The dispersion slope value in 1 550 nm of each mode are 0.093 80 ps/(nm2·km)、0.038 97 ps/(nm2·km),which means that the PCF can achieve dispersion-flattened transmission in the wavelength range of communication.

few-mode fiber;photonic crystal fiber;finite element method;dispersion

TN818

A

1005-8788(2016)06-0036-03

10.13756/j.gtxyj.2016.06.010

2016-06-30

国家自然科学基金资助项目(6127506761571237)

杨静(1992―),女,青海西宁人。硕士研究生,主要研究方向为光纤通信。

施伟华,副教授。E-mail:njupt_shiwh@126.com