相干光通信中的改进型二阶载波相位估计算法

赵 伦,余建国,王任凡,罗 飚

(1.北京邮电大学电子工程学院,北京 100876; 2.武汉光迅科技股份有限公司,武汉430205)

相干光通信中的改进型二阶载波相位估计算法

赵 伦1,余建国1,王任凡2,罗 飚2

(1.北京邮电大学电子工程学院,北京 100876; 2.武汉光迅科技股份有限公司,武汉430205)

针对现有的BPS(盲相位搜索)算法计算复杂度过高的问题,提出了一种基于改进型QPSK(正交相移键控)分区算法的二阶载波相位估计算法,该算法的第一阶采用传统基于部分星座点的P3算法进行粗估计,第二阶采用作者提出的改进型QPSK分区算法补偿剩余的相位噪声。仿真结果表明,该算法的性能与BPS算法相近,但计算复杂度较BPS算法降低了约1/13。

相干光通信;载波相位估计;正交相移键控分区

0 引 言

在相干光通信系统中,相位噪声对系统性能的影响非常大,特别是在高速光通信系统中。采用高阶调制格式会导致星座点之间的欧氏距离减小,即星座点分布会更加密集,对相位噪声也会更加敏感,因而CPE(载波相位估计)算法是相干光通信中DSP(数字信号处理)算法的主要组成部分。对于QPSK(正交相移键控)等相位调制信号,能够采用经典的M次方算法估计相位噪声。但16QAM(正交幅度调制)同时采用了幅度调制和相位调制,且相位分布不均匀,采用M次方算法无法完全移除相位调制信息,因而其不能用于16QAM格式。针对16QAM格式的相位噪声估计,TimoPfau在2009年提出了BPS(盲相位搜索)算法[1],该算法是目前常用的16QAM信号相位噪声估计算法,能够较好地估计16QAM格式的相位噪声,理论上可以用于更高阶QAM格式,但其计算复杂度太大,难以实现实时处理。针对BPS算法的不足,AT&T实验室的Zhou Xiang提出了一种基于BPS和最大似然法的二阶算法[2],第一阶仍采用BPS算法,但只测试少量的相位,即第一阶采用粗估计,第二阶采用最大似然法提高算法的精确度。文献[2]还证明了每增加一个最大似然法估计器所需的开销与单阶BPS算法中增加两个测试相位所需的开销相当。Irshaad Fatadin在2010年提出了一种基于QPSK分区的算法[3](该算法采用了16QAM格式的所有星座点,记为P123算法),基于QPSK的算法计算复杂度远低于BPS算法,但其线宽容忍度较低。针对16QAM格式的CPE算法还有很多,但主要都是基于上述以及它们的改进和组合[4-8]。

本文针对现有的BPS算法计算复杂度过高的问题,提出了一种基于改进型QPSK分区算法的二阶CPE算法。该算法的第一阶采用传统的基于部分星座点的P3算法进行粗估计,第二阶采用本文提出的改进型QPSK分区算法补偿剩余的相位噪声。仿真结果表明,该算法的性能与BPS算法相近,但计算复杂度较BPS算法降低了约1/13。

1 二阶CPE算法的基本原理

图1所示为偏振复用16QAM相干光通信系统框图。在发射端,对激光器发出的光(同时具有X和Y两个偏振方向)进行偏振复用16QAM后送入单模光纤中传输,并对光信号进行放大。在接收端,偏振分束器接收到的光信号被分成X方向和Y方向两路光信号,因此接收端需要准备一个本地激光器并使用偏振分束器将本地激光器发出的光信号分成X方向和Y方向两路光信号。对于X方向的两路光信号采用90°混频器进行混频,并使用两个平衡探测器进行探测,以消除直流成分。对Y方向的两路光信号采取与X方向两路光信号相同的处理方法。随后采用4个模/数转换器将4个平衡探测器输出的模拟电信号转换成数字信号,最后使用DSP算法对4路数字信号进行处理,以补偿信号传输中的损失。DSP算法包括隔直流、归一化、低通滤波、重抽样、正交化、色散补偿、非线性补偿、定时恢复、自适应均衡、频偏估计和相位估计等。本文主要考虑相位估计算法,因此假设已经对除相位噪声外的各种损伤进行补偿。

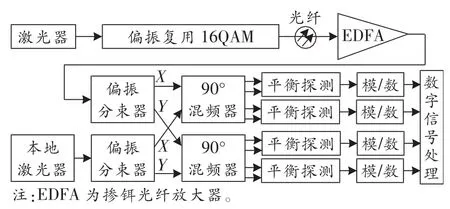
图1 偏振复用16QAM相干光通信系统框图

图2所示为本文所提用于相干光通信系统中16QAM信号载波相位估计的二阶CPE算法框图。第一阶采用常规方法补偿部分相位噪声,记为P3算法,第二阶采用基于改进的QPSK分区算法补偿剩余的相位噪声,记为IP(改进分区)算法。因而将提出的二阶CPE算法记为P3+IP算法。

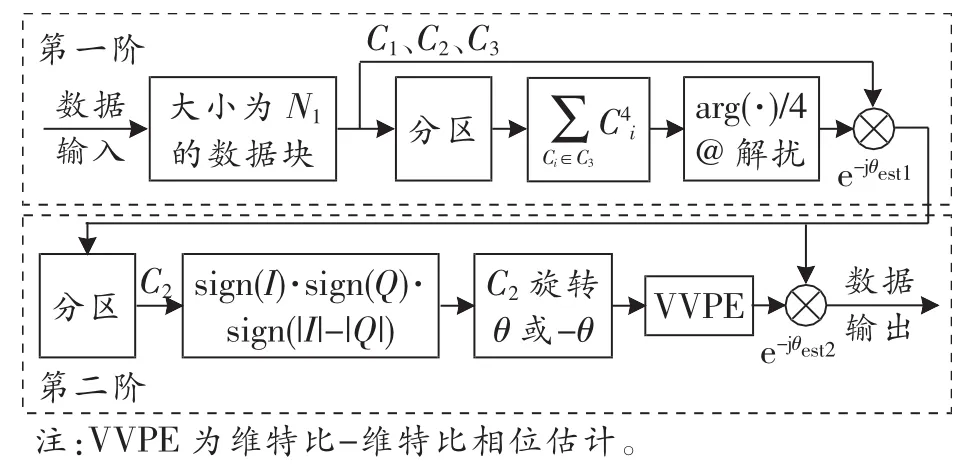
图2 P3+IP算法框图

第一阶的处理流程如下:首先将输入信号分为若干个大小为N1的数据块,对于每个数据块,根据半径将其分为C1、C2、C33个区,选择属于C3分区中的数据符号进行四次方操作,从而移除相位调制信息,然后将四次方后的数据取相位并除以4得到相位噪声,并采用相位解扰来降低周跳的影响(所谓周跳就是相位划过±π时由于相位周期特性的限制。而发生的大小为2π的相位跳变),最后用估计得到的值对输入数据进行补偿。

第二阶的处理流程如下:将第一阶的输出作为第二阶的输入,第二阶处理的数据块长度N2与第一阶的长度N1相同,首先根据半径将该数据块分为C1、C2、C33个区,由于第一阶仅进行了相位旋转,并没有改变信号的幅度,因此可将第一阶中数据分区的结果用于第二阶。相位分区图如图3所示,将[0,π]等分为1～4四个区间,将[―π,0]等分为5～8四个区间,C2中的每个数据符号的相位值都位于这8个区间中的一个。选取属于C2分区中的数据计算sign(I)·sign(Q)·sign(|I|―|Q|),其中I、Q分别为分区C2中数据的实部和虚部。

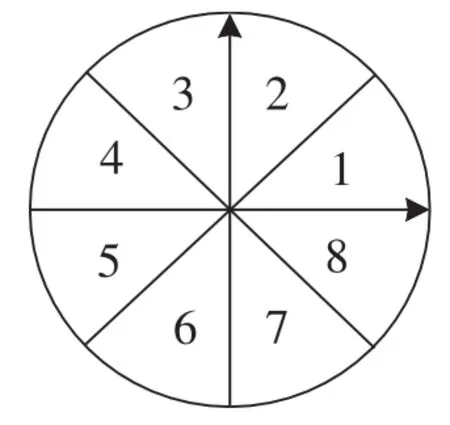
图3 相位分区图

表1所示为每个区间sign(I)·sign(Q)·sign(|I|―|Q|)的计算值。由表1可知,区间1、3、5和7中的sign(I)·sign(Q)·sign(|I|―|Q|)值为正,而区间2、4、6和8中的值为负。sign(I)·sign(Q)·sign(|I|―|Q|)为正值的区间中的数据符号对应的相位旋转为―θ,为负值的区间中的数据符号对应的相位旋转为θ。

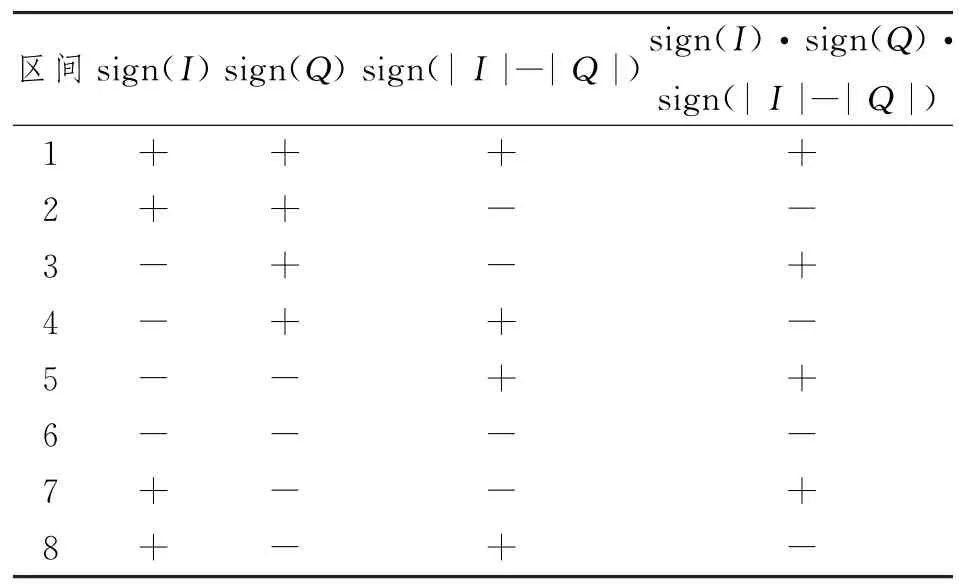
表1 sign(I)·sign(Q)·sign(|I|―|Q|)的计算值

因此,可根据sign(I)·sign(Q)·sign(|I|―|Q|)的计算值正负判断C2分区中的相位旋转的方向,并对C2进行相应的旋转,使得C2分区中的数据也位于QPSK的4个星座点附近,然后用常规的

2 仿真结果及分析

采用OptiSystem软件搭建仿真平台对改进的二阶CPE算法性能进行仿真分析。图4所示为偏振复用16QAM传输系统仿真平台的系统框图,BER Test Set器件的功能是产生二进制比特序列,并将该二进制比特序列与电域处理后的二进制比特序列进行对比,从而计算系统的BER(误码率)等参数,产生的二进制比特被复制成两份,一份送到判决器中作为判决参考值,另一份送入发射机中,发射机的作用是产生偏振复用16QAM的光信号,在送入光纤前使用OA(光放大器)调整入纤光功率,在光纤传输后通过Set OSNR器件设置OSNR(光信噪比),然后送入基于相位分集和偏振分集的相干接收机对光信号进行处理,得到的4路电信号分别对应X偏振方向的同相、正交分量以及Y偏振方向的同相、正交分量。之后使用DSP模块对接收到的电信号进行补偿,DSP模块的功能包括隔直流、归一化、低通滤波、重抽样、正交化、色散补偿、非线性补偿、定时恢复、自适应均衡和频偏估计。为了验证所提P3+IP算法的性能,在DSP中没有进行CPE操作,而是用DSP后面的Matlab器件完成二阶CPE的功能,该器件提供OptiSystem和Matlab的接口。在相位恢复后使用Decision模块进行星座判别并进行QAM序列解调,然后将数据送入BER Test Set统计传输后的错误比特数及BER等参数。

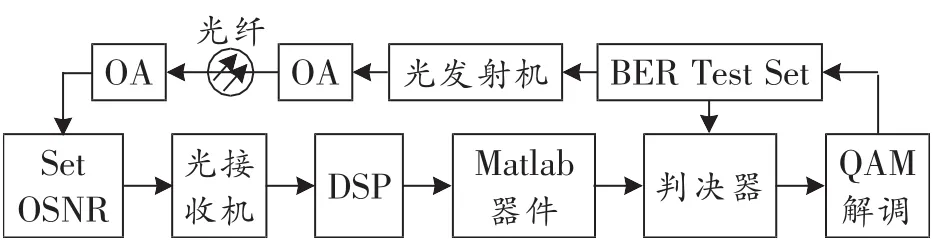
图4 偏振复用16QAM传输系统仿真平台的系统框图

由于是偏振复用16QAM系统,112 Gbit/s的比特率对应的符号率为14 Gbaud,其他仿真参数设定如下:序列长度为524 288;每个符号抽样数为4;保护比特为100;发射机激光器波长为1 550 nm,功率为0 dBm;接收机激光器波长为1 550.001 nm,功率为10 d Bm;光纤长度为160 km;色散系数为16.75 ps/(nm·km);PMD(偏振模色散)系数为0.05 ps/km。

本文首先将P3+IP算法与BPS、P3和P123算法的性能进行对比分析,图5所示为在仿真平台上采用不同的CPE算法进行相位噪声估计时BER与OSNR的关系曲线。将收发激光器的线宽均设为100 k Hz,对应激光器的线宽和码元周期乘积(即ΔL·Ts)约为1.4×10―5。图中,N表示对应的CPE算法每次处理数据块的长度,N1和N2分别表示二阶CPE算法第一阶和第二阶处理的数据块的长度,由图可以看出,P3算法的性能最差,P123算法次之,BPS算法的性能最好,而本文所提的P3+IP算法的性能介于BPS和P123算法之间。图中几种算法的性能差距不大是由于ΔL·Ts的值较小。从图中还可以看出,OSNR约为17.85 dB时,采用IP3+IP算法可以达到1×10―3的BER。

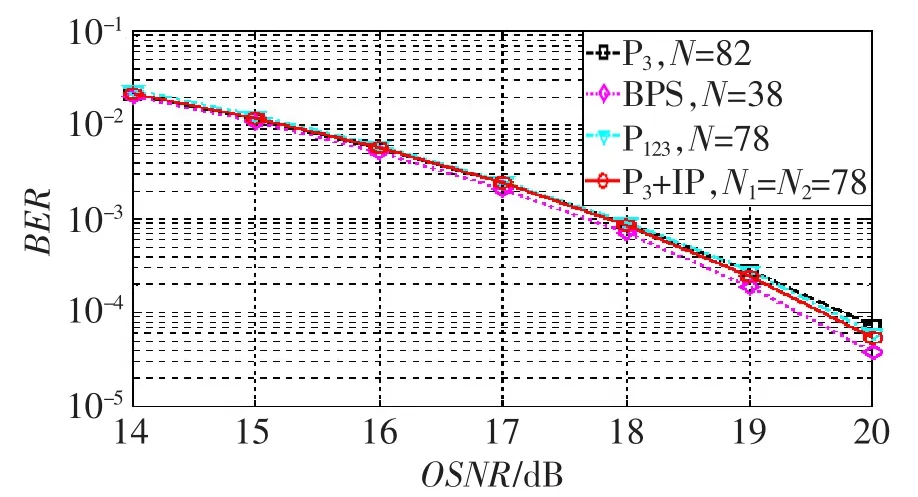
图5 采用不同CPE算法时BER与OSNR的关系曲线

图6 和图7分别为OSNR为18 d B时使用P3+IP算法估计出的相位噪声的相位值以及进行相位噪声补偿后的星座图(X偏振方向)。由图6可知,相位噪声值没有出现跳变,这是由于本文采用了相位解扰。图7的星座图总体来说还比较清晰。

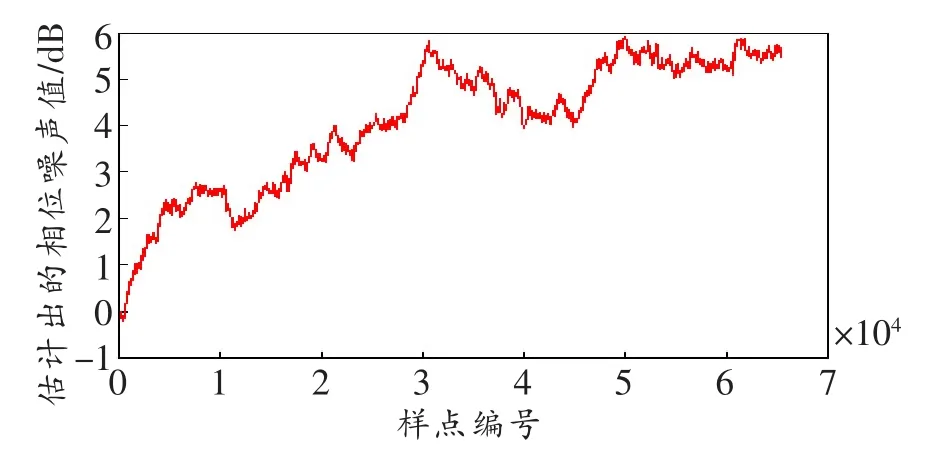
图6 P3+IP算法的相位噪声

图8 为OSNR为18 d B时采用不同的CPE算法得到的线宽符号持续时间乘积与BER的关系曲线。其中线宽符号持续时间为1/14 ns,而图中的7个测试点对应的收发激光器的总线宽分别为7、70、

210、490、700、840和1 000 k Hz。从图中可以看出,P3+IP算法的性能介于P123算法和BPS算法之间,且线宽符号持续时间乘积较大时,所提算法的BER性能相对P3算法有一定的优势。

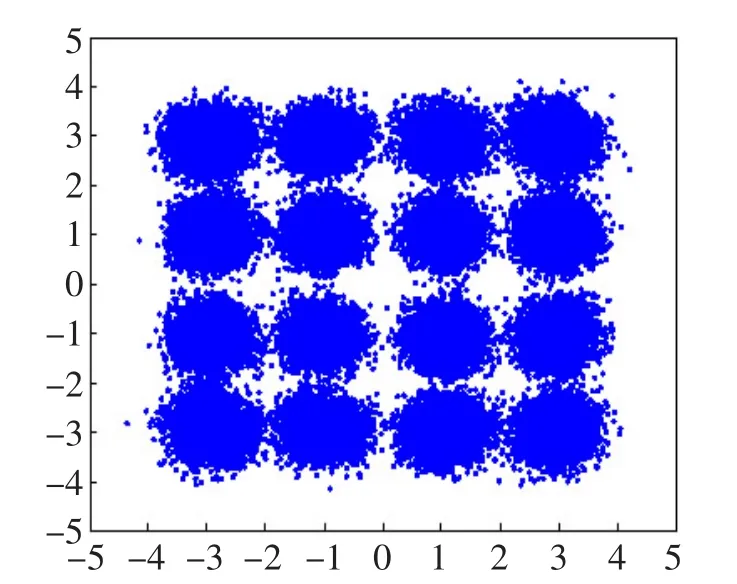
图7 P3+IP算法的星座图

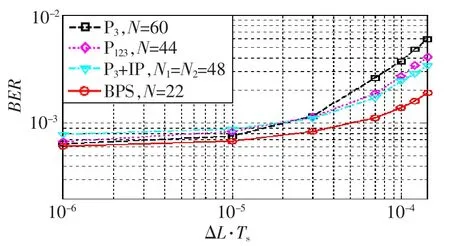
图8 线宽符号持续时间乘积与BER关系曲线

算法复杂度也是衡量CPE算法的重要指标之一,过于复杂的算法难以在硬件上实现。已有文献对算法复杂度的统计方法进行了研究[7-9],据此得到数据块长度为N的4种CPE算法的计算复杂度如表2所示,其中B表示BPS算法的测试相位个数。如果用实数乘法器、实数加法器、比较器的总个数以及查表、判决的总次数的和表示算法复杂度,那么当N=100时,4种算法的总运算复杂度分别为1 354、3 354、3 204和42 302。据此可知,与P3算法相比,P3+IP算法复杂度增加了2.3倍;与P123算法相比,P3+P123算法复杂度略低,性能更好;与BPS算法相比,性能略差,但算法复杂度降低了约1/13。

表2 4种CPE算法的复杂度

3 结束语

本文提出了一种P3+IP算法,在第一阶使用传统的P3算法进行粗估计,在第二阶使用简单的符号乘法就可以判断16QAM星座中间圈上点的位置并进行相应的相位旋转,使得16QAM星座成为普通的QPSK星座,能够方便地估计相位噪声。该算法的复杂度比P123算法略低,但性能比P123算法更好。所提算法的性能比BPS算法略差,但在复杂度上却比BPS算法降低了约1/13。

[1]Pfau T,Hoffmann S,NoéR.Hardware-efficient coherent digital receiver concept with feedforward carrier recovery for M-QAM constellations[J].IEEE Journal of Lightwave Technology,2009,27(8):989―999.

[2]Zhou X.An improved feed-forward carrier recovery algorithm for coherent receivers with M-QAM modulation format[J].IEEE Photonics Technology Letters,2010,22(14):1051―1053.

[3]Fatadin I,Ives D.Laser Linewidth Tolerance for 16-QAM Coherent Optical Systems Using QPSK Partitioning[J].IEEE Photonics Technology Letters,2010,22(9):631―633.

[4]Li X,Cao Y.A Simplified Feedforward Carrier Recovery Algorithm for Coherent Optical QAM System [J].IEEE Journal of Lightwave Technology,2011,29 (5):801―807.

[5]Li J,Li L,Tao Z,et al.Laser-linewidth-tolerant feedforward carrier phase estimator with reduced complexity for QAM[J].IEEE Journal of Lightwave Technology,2011,29(16):2358―2364.

[6]Ke J,Zhong K,Gao Y,et al.Linewidth-Tolerant and Low-Complexity Two-Stage Carrier Phase Estimation for Dual-Polarization 16-QAM Coherent Optical Fiber Communications[J].IEEE Journal of Lightwave Technology,2012,30(24):3987―3992.

[7]Zhong K,Ke J,Gao Y,et al.Linewidth-Tolerant and Low-Complexity Two-Stage Carrier Phase Estimation Based on Modied QPSK Partitioning for Dual-Polarization 16-QAM Systems[J].IEEE Journal of Lightwave Technology,2013,31(1):50―57.

[8]Gao Y,Lau A P T,Lu C,et al.Low-complexity twostage carrier phase estimation for 16-QAM systems using QPSK partitioning and maximum likelihood detection[C]//OFC 2011,Los Angeles,USA:OSA,2011: OMJ6.

[9]钟康平.DP-16QAM相干光通信系统关键技术的研究[D].北京:北京交通大学,2014.

An Improved Two-Stage Carrier Phase Estimation Algorithm in Coherent Optical Communication

ZHAO Lun1,YU Jian-guo1,WANG Ren-fan2,LUO Biao2
(1.School of Electronic Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China; 2.Accelink Technologies Co.,Ltd.,Wuhan 430205,China)

Aiming at the problem of high computational complexity of existing Blind Phase Search(BPS)algorithm,the thesis proposes a two stage carrier phase estimation algorithm based on improved QPSK partition algorithm.The first stage of the algorithm is based on traditional P3algorithm,which is used to realize rough estimation.The second stage of the algorithm is based on the proposed improved QSPK partition algorithm,which is used to compensate the residual phase noise.The simulation results show that the performance of this algorithm is similar to that of BPSalgorithm.However,the computational complexity is about 13 times lower than that of the BPS algorithm.

coherent optical communication;carrier phase estimation;QPSK partition

TN914

A

1005-8788(2016)06-0001-04

10.13756/j.gtxyj.2016.06.001

2016-06-14

国家“八六三”计划资助项目(2015AA016901);国家自然科学基金面上资助项目(61377079)

赵伦(1987―),男,湖北孝感人。博士研究生,主要研究方向为相干光通信、无线通信及光载无线通信。