多目标智能规划算法研究*

金 琦 蒋 敏 宋子健

(1.火箭军工程大学 西安 710025)(2.66109部队 北京 100044)



多目标智能规划算法研究*

金 琦1蒋 敏1宋子健2

(1.火箭军工程大学 西安 710025)(2.66109部队 北京 100044)

为了解决多目标规划难的问题，论文在阐述了相关问题的基础上，首先对多目标规划方法进行了描述；而后设计完成了GAPS-MMA算法，对其算法的主要部分，即适应度值的计算和Pareto解集的更新进行了重点研究，给出了GAPS-MMA算法流程；最后，以某飞行器航迹规划为例，运用GAPS-MMA算法与模拟退火算法进行对比分析，得到了更好的全局最优解。通过算例证明， GAPS-MMA算法是更为科学的、合理的。

多目标; 智能规划; 进化算法; GAPS-MMA

Class Number TN99

1 引言

多目标优化问题中各目标之间通过决策变量相互制约，对其中的一个目标优化必须以牺牲其他目标作为代价，而且各目标的物理意义往往又不一致，因此很难评价多目标问题解的优劣性[1～3]。与单目标优化问题的本质区别在于，多目标优化问题的解不是惟一的，而是存在一个最优解集合，即Pareto最优解集[4～5]。Pareto最优解集中的元素，就所有目标而言是彼此不可比较的。

在过去的二十年中，进化算法(Evolutionary Algorithms，EA)[6～8]作为多目标优化问题新的求解方法受到了广泛关注。同时，作为一种概率性算法，进化算法应用于多目标优化问题时，基于模式定理而非梯度信息产生群体中的最优(满意)个体，不像其他传统的精确算法那样对目标函数和约束条件有诸多限制。基于进化计算的多目标优化方法大致分为三类[9～12]：经典的求解多目标优化进化算法，非聚合、非基于Pareto占优的多目标优化进化算法，基于Pareto占优的多目标优化进化算法。这三种方法均是针对连续型多目标优化问题，对于本文探讨的多约束多目标非线性任务规划问题无法直接适用，需要设计满足其独特需求的进化算法。基于这样的指导思想，本文提出了多个任务规划目标情形下的基于Pareto解集的遗传进化算法(Genetic Algorithm based Pareto Set for Multi-objective Mission-planning Algorithm，GAPS-MMA)。

2 多目标任务规划描述

通常对于任务规划而言，一般涉及三个任务规划指标：任务完成风险度最小指标F1、任务完成时间最短指标F2以及任务资源消耗最少指标F3。其中，对于规划指标F3的理解可基于两方面的认识：一方面，可以在要求任务完成风险度最小的情形下，追求任务资源消耗最少，规划指标等同于F1∪F3；另一方面，可以在要求任务完成时间最短的情形下，追求任务资源消耗最少，规划指标等同于F2∪F3。所以，规划指标F3一定程度上表现为多目标规划的形式。综上，多目标任务规划可归结为以下几种情形，如表1所示。

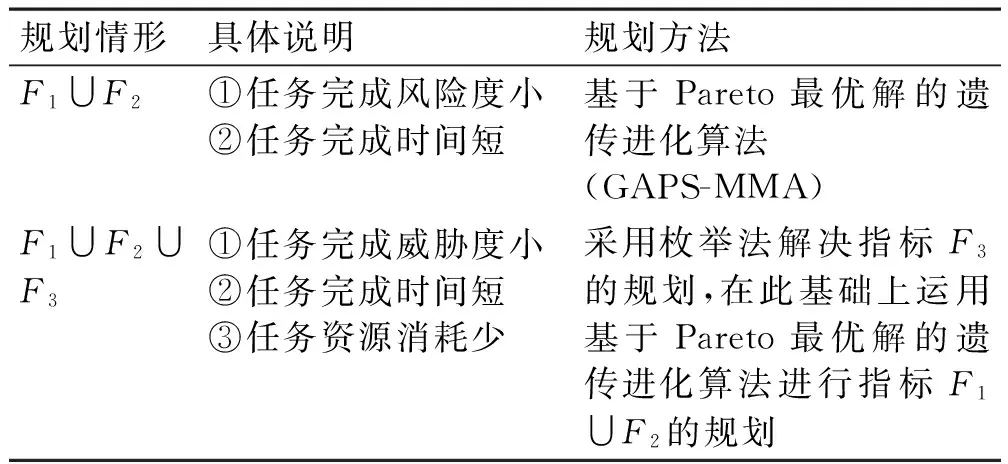
表1 不同情形下的多目标任务规划方法

由上表可以看出，第二种规划情形只需在第一种规划情形上应用枚举法即可解决，因此，多目标任务规划着重在于解决第一种情形，即任务完成风险度和任务完成时间的组合问题。同时，对于多目标的任务规划问题，主体算法重点在于适应度值计算以及规划解集的选择更新，下面重点对这两方面进行详细论述，其它次要部分不再赘述。

3 多目标智能规划算法

3.1 适应度值计算

(1)

s(Xi)=|S(Xi)|

(2)

其中|·|表示集合的规模。

2) 最近邻密度信息d(Xi)

由于个体Xi的Pareto占优数是按照弱占优关系计算的，当Pareto解集中两个个体的Pareto占优数相同时，最近邻密度信息可进一步刻画两个个体在更细节层次上的优劣关系。最近邻密度概念来源于Zitzler和Thiele的改进SPEA算法。

(3)

(4)

3.2 Pareto解集更新

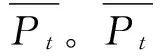
主要从三个方面来获取Pareto最优解：Pareto占优关系、最近邻密度信息以及相邻个体的欧式距离。首先基于个体的Pareto占优关系，将非劣解放入Pareto解集中。如果Pareto解集规模超过限制，则采用如下的裁剪方法：

1) 基于个体的最近邻密度信息，裁剪较劣个体；

2) 如果最近邻密度信息仍然不能确定两个个体的优劣关系时，则采用临近排挤算法对较劣个体进行裁剪。具体步骤为：

(3)找出欧式距离最短的两相邻个体Xj和Xj+1；

(4)比较dj-1和dj+1的大小。若dj-1dj+1，则裁剪个体Xj+1；

3) 当上述方法仍然不能确定非劣解个体的优劣关系时，则随机选择各层次上适应度相同的解个体予以裁剪。

Step 2：生成第t+1代外部Pareto解集：

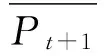
3.3 GAPS-MMA算法流程

综上所述，建立多个任务规划目标情形下的任务规划算法如下：

Step 1：输入任务规划信息；

Step 2：设置任务规划目标：F1∪F2；

Step 3：设置遗传算法控制参数以及结束条件(在此为最大迭代次数T)；

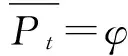
Step 5：按照传统染色体解码算法和初始种群生成算法随机生成初始种群P0；

Step 9：依据适应度计算公式计算种群P″t中个体的适应度值；

Step 10.1：初始化Pt+1=φ

Step 10.2：Fori=1 to Sizepop，do

Step 11:t=t+1。如果t>T或者满足其他结束条件，进入下一步，否则，转入Step6；

4 算例

以某飞行器航迹规划为例，其目标主要有两个，即飞行风险小和时间短(飞行距离短)。

在水平区域为600km×600km的规划空间中，采用地形高程数据进行实验，图1、图2分别为数字地图的三维显示图和数字地图的等高线图。为了后续方便展示规划结果，结合飞行器航迹实际情况，采用简图形式展示。

图1 数字地图的三维显示

图2 数字地图的等高线图

飞行器起始点的平面坐标为(60，60)，目标点的平面坐标为(600，480)，干扰源平面坐标分别为(300，200)、(500，400)。以边长为60km的网格对规划空间进行划分，每个网络节点的地形高程为其所包含区域中所有地形高程的平均值。

通过仿真计算，分别给出模拟退火算法和GAPS-MMA算法在不同情况下的多目标规划方案如下：

情况一：在仅考虑航迹长度(时间最短)的影响下，模拟退火算法和GAPS-MMA算法分别给出最优航迹如图3所示，虚线表示GAPS-MMA算法给出的规划航迹，实线表示模拟退火算法给出的规划航迹。

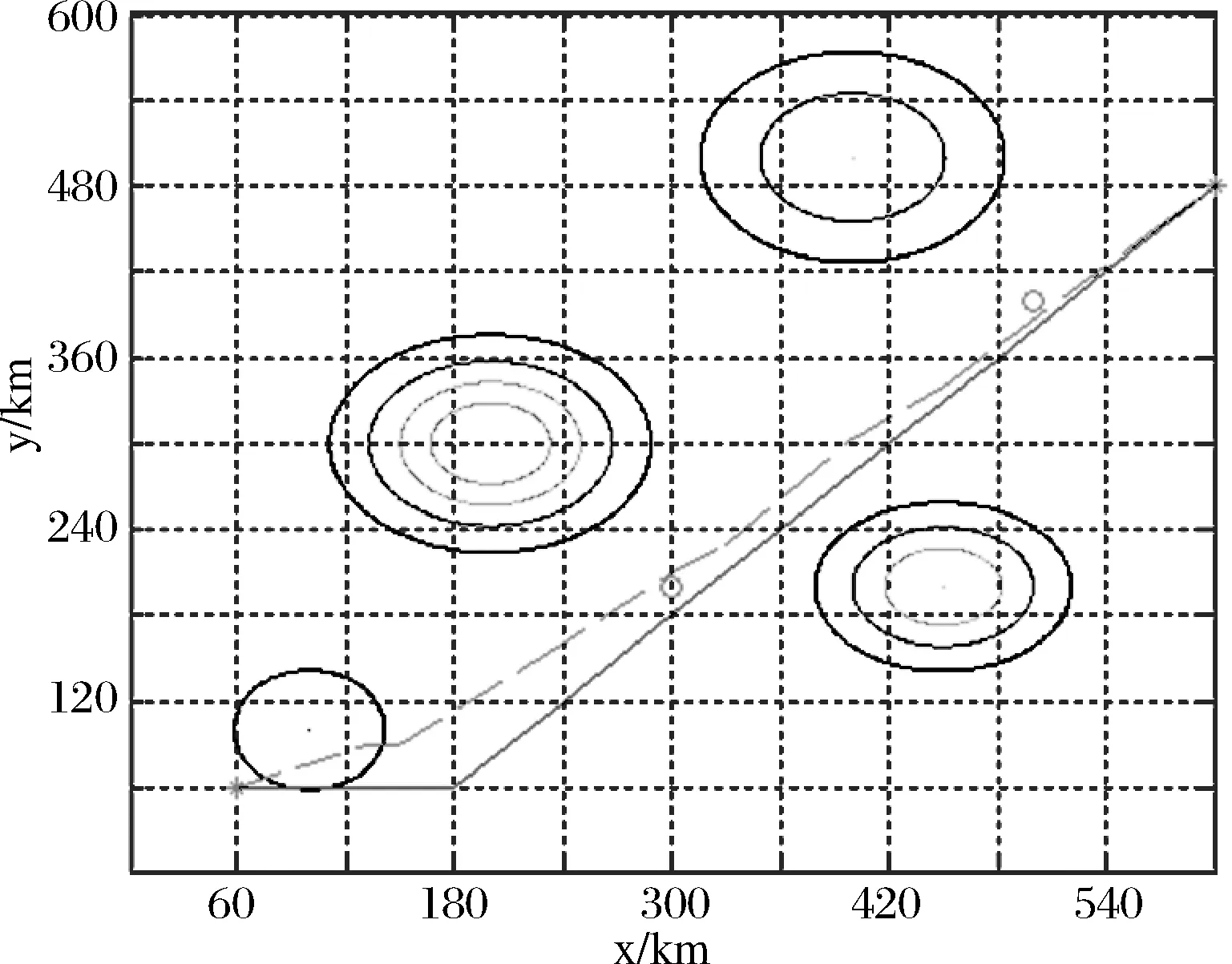
图3 考虑航迹长度影响的全局最优航迹平面简图

情况二：在仅考虑风险的影响下，最优航迹应尽可能远离威胁，模拟退火算法和GAPS-MMA算法分别给出最优航迹如图4所示。

图4 考虑风险影响的全局最优航迹简图

情况三：综合考虑两种因素的影响，得到全局最优规划结果为三种情况，如图5所示。

从以上仿真实验可以看出，由GAPS-MMA算法得到的结果是更为合理的，能够在全局范围内确定出最优航迹，所用规划时间不超过3s。同时，这些最优航迹结果较为稳定，具有一定的鲁棒性，由此确定的全局最优航迹的范围是正确可靠的，也证明，对于多目标规划而言，GAPS-MMA算法是更科学合理的。

图5 考虑时间和风险两种影响的全局最优航迹简图

5 结语

对于多目标规划而言，很难得到多目标规划问题的最优解，进化算法给出了解决问题的新思路。本文在阐述了相关问题的基础上，首先对多目标规划方法进行了描述；而后设计完成了GAPS-MMA算法，对其算法的主要部分，即适应度值的计算和Pareto解集的更新进行了重点研究，给出了GAPS-MMA算法流程；最后，以某飞行器航迹规划为例，运用GAPS-MMA算法与模拟退火算法进行对比分析，得到了更好的全局最优解。通过算例证明， GAPS-MMA算法是更为科学的、合理的。

[1] 任晓莉.LSO改进CGA解决多目标作业车间调度问题[J].计算机应用与软件,2015,32(3):60-64. REN Xiaoli. IMPROVING CGA BY LSO FOR MULTIPLE-OBJECTIVE JOB SHOP SCHEDULING PROBLEM[J]. Computer Applications and Software,2015,2(3):60-64.

[2] Tan Y, Zhu Y. Fireworks algorithm for optimization[C]// Berlin: Springer,2010:355-364.

[3] 王培崇,高文超,钱旭,等.应用精英反向学习的混合烟花爆炸优化算法[J].计算机应用,2014,34(10):886-2890. WANG Peichong, GAO Wenchao, QIAN Xu, et al. Hybrid fireworks explosion optimization algorithm using elite opposition-based learning[J]. Journal of Computer Applications,2014,34(10):886-2890.

[4] 陈刚.飞行航线的自动规划方法研究[D].长沙:国防科技大学,2010.CHEN Gang. Study on the method of flight path automatic planning[D]. Changsha: National University of Defense Technology,2010.

[5] 潘全科.智能制造系统多目标车间调度研究[D].南京:南京航空航天大学,2013. PAN Quanke. Research on multi objective job shop scheduling in Intelligent Manufacturing System[D]. Nanjing: Doctoral Dissertation of Nanjing University of Aeronautics & Astronautics,2013.

[6] 刘衍民,隋常玲,牛奔.解决约束优化问题的改进粒子群算法[J].计算机工程与应用，2011,47(12):23-26. LIU Yanmin, SUI Changling, NIU Ben. Improved particle swarm optimizer for constrained optimization problems[J]. Computer Engineering and Applications,2011,47(12):23-26.

[7] 叶媛媛.多UCAV协同任务规划方法研究[D].长沙:国防科技大学,2010. YE Yuanyuan. Research on multi UCAV cooperative task planning method[D]. Changsha: National University of Defense Technology,2010.

[8] 刘长平,叶春明.基于逻辑自映射的变尺度混沌粒子群优化算法[J].计算机应用研究,2011,28(8):2825-2827. LIU Changping ,YE Chunming. Mutative scale chaos particle swarm optimization algorithm based on self logical mapping function[J]. Application Research of Computers,2011,28(8):2825-2827.

[9] 谭营,郑少秋.烟花算法研究进展[J].智能系统学报,2014,9(5):515-528. TAN Ying, ZHENG Shaoqiu. Recent advances in fireworks algorithm[J]. CAAI Transactions on Intelligent Systems,2014,9(5):515-528.

[10] Coello Coello C A, Lechuga M S. MOPSO: a proposal for multiple objective particle swarm optimization[M]. Washington DC: IEEE,2012:1051-1056.

[11] 程临燕,张保会,郝治国,等.基于综合灵敏度分析的快速控制算法研究[J].电力自动化设备,2011,29(4):46-49. CHENG Linyan, ZHANG Baohui, HAO Zhiguo, et al. Fast control algorithm based on integrative sensitivity analysis[J]. Electric Power Automation Equipment,2011,29(4):46-49.

[12] 覃朝勇,刘向,郑建国.求解多目标job-shop生产调度问题的量子进化算法[J].计算机应用研究,2010,27(3):849-852. QIN Chaoyong, LIU Xiang, ZHENG Jianguo. Quantum-inspired evolutionary algorithm for multi-objective job-shop scheduling[J]. Application Research of Computers,2010,27(3):849-852.

Multi-objective Intelligent Planning Algorithm

JIN Qi1JIANG Min1SONG Zijian2

(1. Rocket Force Engineering University, Xi’an 710025)(2. No. 66109 Troops of PLA, Beijing 100044)

In order to solve the difficult problem of multi-objective planning, on the basis of introducing of relevant issues, firstly the paper describes multi-objective planning methods, then GAPS-MMA (Genetic Algorithm based Pareto Set for Multi-objective Mission-planning Algorithm) is completed, the main part of the algorithm, namely computing fitness value and updating Pareto sets are focused on research, and the process of GAPS-MMA is given. Finally, an air vehicle route planning for example is taken, through the comparison for GAPS-MMA and SA (simulated annealing algorithm), the better global optimal solution is gotten by GAPS-MMA. It is proved that GAPS-MMA algorithm is more scientific and reasonable by the example.

multi-objective, intelligent planning, evolutionary algorithm, GAPS-MMA

2016年5月12日,

2016年6月14日

金琦，女，研究方向：通信工程。蒋敏，女，研究方向：通信工程。宋子健，男，工程师，研究方向：电子工程。

TN99

10.3969/j.issn.1672-9722.2016.11.014