基于最小二乘法的雷达组网航迹关联性能分析*

陈 欣

(91404部队 秦皇岛 066000)



基于最小二乘法的雷达组网航迹关联性能分析*

陈 欣

(91404部队 秦皇岛 066000)

航迹关联是雷达组网数据融合系统中的一项关键技术,论文构建一个满足实际需求的较为完备的基于最小二乘法的雷达组网航迹关联数据处理系统，并对系统的性能加以分析,最后应用递归最小二乘算法进行偏差估计。该系统有效地增加了系统内的目标航迹信息利用率，并在实际应用中验证了其有效性。

最小二乘法; 组网雷达; 航迹关联

Class Number TP391

1 引言

随着现代战争越来越复杂,单雷达系统已经不能满足作战需求，一方面受盲区影响降低了探测范围,另一方面容易被敌方电子侦察系统侦察到而被实施干扰或受到攻击,使其生存能力下降,因此雷达组网信息融合技术目前已经在军事上得到了广泛的应用。雷达组网和单雷达系统相比不仅可以扩展雷达系统在空间距离和方位上的覆盖范围，还有效地增加了系统内的目标航迹信息利用率，从而提高目标航迹信息的可信度和精度，增强了整个作战系统对目标的检测和识别能力。组网雷达系统中每部雷达都收集了大量的目标航迹信息,那么如何判断来自于不同雷达系统的两条航迹是否代表同一目标,这就是航迹关联问题[1]。

当目标航迹间相距很远并且没有干扰、杂波的情况下,关联问题比较简单。但在多目标、干扰、杂波、噪声和交叉、分岔航迹较多的场合下,航迹关联问题就变得复杂。再加上各雷达系统之间在距离或方位上的组合失配、传感器位置误差、目标高度误差、坐标变换误差等因素的影响,使有效关联变得更加困难[2]。如果用传统的统计方法对航迹进行相关处理,需要重新建立各个机动目标运动模型,这将会增大计算负荷,使系统难以满足实时性的要求。因此,本文采用基于最小二乘法的航迹相关方法,即用最小二乘法拟合出目标的运动轨迹,以避免建立大量的目标状态模型。

2 航迹关联相关原理

航迹关联过程不单指点迹/航迹的相关，还包括相关之前的传感器数据预处理，数据格式与坐标变换，数据的有效性检查，数据时间对准，数据的空间融合，以及相关之后的航迹滤波与更新，直至得到完整的目标航迹数据[3]。

组网雷达系统目标航迹关联处理流程如图1所示[4],雷达系统内的各雷达单元分别对各自的目标数据进行距离、方位上的预处理，生成局部航迹，然后将局部航迹送入航迹关联模块。航迹关联模块先对各雷达航迹数据从不同的时-空坐标参考系统变换、对准到系统统一的时-空坐标参考系统，即航迹数据的时-空对准，再校正系统内各部雷达的系统误差，然后采用加权统计距离检测法将输入的对应同一目标的多部雷达的单雷达航迹关联到一已存在的系统航迹或新生的系统航迹。最后，对系统航迹数据运用卡尔曼滤波[5]，处理成为单雷达航迹。

图1 目标航迹关联处理流程图

3 基于最小二乘法的航迹关联相关准则

基于最小二乘法的航迹相关准则如下[6]：利用各航迹连续10次的点迹建立各航迹运动方程,依本平台航迹采样时间为基准,将远程航迹采样值依次外推到本平台的采样时刻值；求出远程航迹到本平台航迹对应时刻之间的距离，如果距离小于关联门限K(K为所关联航迹中航迹质量较低的航迹质量半径)，则记为1，否则记为0。最终累加1的结果，若1值累加结果大于等于7，则认为两条航迹是相关的,是同一目标航迹，并且选择航迹质量较好一条作为目标航迹。

4 组网雷达系统偏差估计

本地的跟踪和中心的数据关联都是以均方估计准则消除随机误差,系统误差使观测数据相对真实值产生固定的偏移,对系统误差的消除可以通过最小平方法求出各雷达系统误差的估值,然后再对测量数据进行一次性的配准,然后对各个雷达航迹进行误差补偿,同时得到作为系统参数的各雷达的误差协方差矩阵[7]。

假设各部雷达的定位精确,即不存在定位误差；雷达的系统偏差发生在距离和方位观测上,并且均为常数。应用最小二乘方法能够得到系统的偏差估计值。现以两部雷达为例,说明偏差估计的过程。

设雷达i的系统偏差向量为

其中,m为组网雷达数。目标的运动状态方程为

x(k)=Fx(k)+v(k)

(1)

式中:状态向量x和状态转移矩阵F的定义如下。

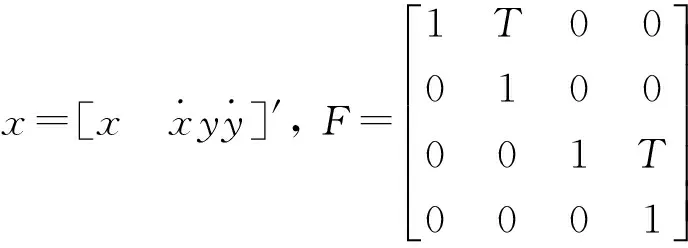
式中:T为采样时间间隔,v(k)为零均值高斯白噪声,其协方差矩阵为

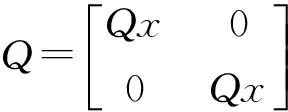
式中:Qx,Qy为X、Y方向的过程噪声协方差矩阵。

4.1 雷达系统偏差

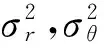
zi(k)=Hx(k)+Bi(k)bi+wi(k)

(2)

式中:Bi(k)bi为直角坐标系下雷达系统偏差向量,wi(k)为直角坐标系下观测随机噪声。

4.2 系统偏差观测模型

假设雷达本地生成航迹时只存在随机误差,不存在系统偏差。观测方程如下:

zi(k)=H(k)x(k)+wi(k)

(3)

式中未考虑系统偏差,因此导致了观测模型失配。对于两部雷达i=1,2,构造系统偏差向量的伪观测向量对偏差进行估计。

-B2(k+1)b2+w1(k+1)-w2(k+1)

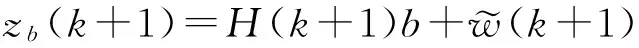
(4)

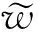
H(k+1)=[B1(k+1)-B2(k+1)]

(5)

(6)

w(k+1)=w1(k+1)-w2(k+1)

(7)

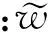
R(k+1)=R1(k+1)+R2(k+1)

(8)

4.3 系统偏差的递归最小二乘估计

系统偏差为未知常数，在式(10)的基础上可以应用递归最小二乘估计器进行估计。递归可以在两个层面上进行: 1) 在同一处理周期内的多个目标之间； 2) 在多个处理周期之间。

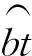
如果在k时刻可用于偏差估计的目标数为n,对每个目标t(t=1,…,n)进行如下操作。

1) 计算新的伪偏差观测量:

(9)

2) 计算偏差更新增益和残差[10]：

Gt(k)=Σt(k-1)Ht(k)′[Ht(k)Σt(k)Ht(k)′+Rt(k)]-1

(10)

(11)

3) 更新系统偏差估计及其协方差矩阵:

(12)

Σt(k) =[I-Gt(k)Ht(k)]Σt-1(k)

[I-Gt(k)Ht(k)]′+Gt(k)Rt(k)Gt(k)′

(13)

对n个目标的操作都完成后,在下一周期进行偏差估计的初始值设置为[11]

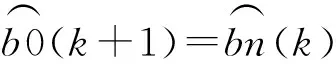
(14)

Σ0(k+1)=Σn(k)

(15)

5 测试结果分析

根据上述的航迹算法，以2部单部雷达跟踪同一个机动目标为例。2部雷达的体制相同，传感器的采样周期相同，通过GPS数据作为真值数据，如图2和图3所示，图为其中某单部雷达跟踪精度一次差与航迹关联后一次差对比曲线，2部雷达传感器的采样周期相同，GPS数据作为真值数据。三角散点标记曲线为单部雷达航迹一次差曲线，黑色虚线为航迹关联后一次差曲线，可以看出，在密集的空情环境下，利用该系统进行雷达组网不但实现了目标的准确关联，而且无论是在目标航行的直线段还是机动阶段，关联后航迹随机误差减小。雷达组网比单个雷达滤波形成的航迹的距离跟踪误差明显减小，对机动目标的跟踪精度得到了提高。

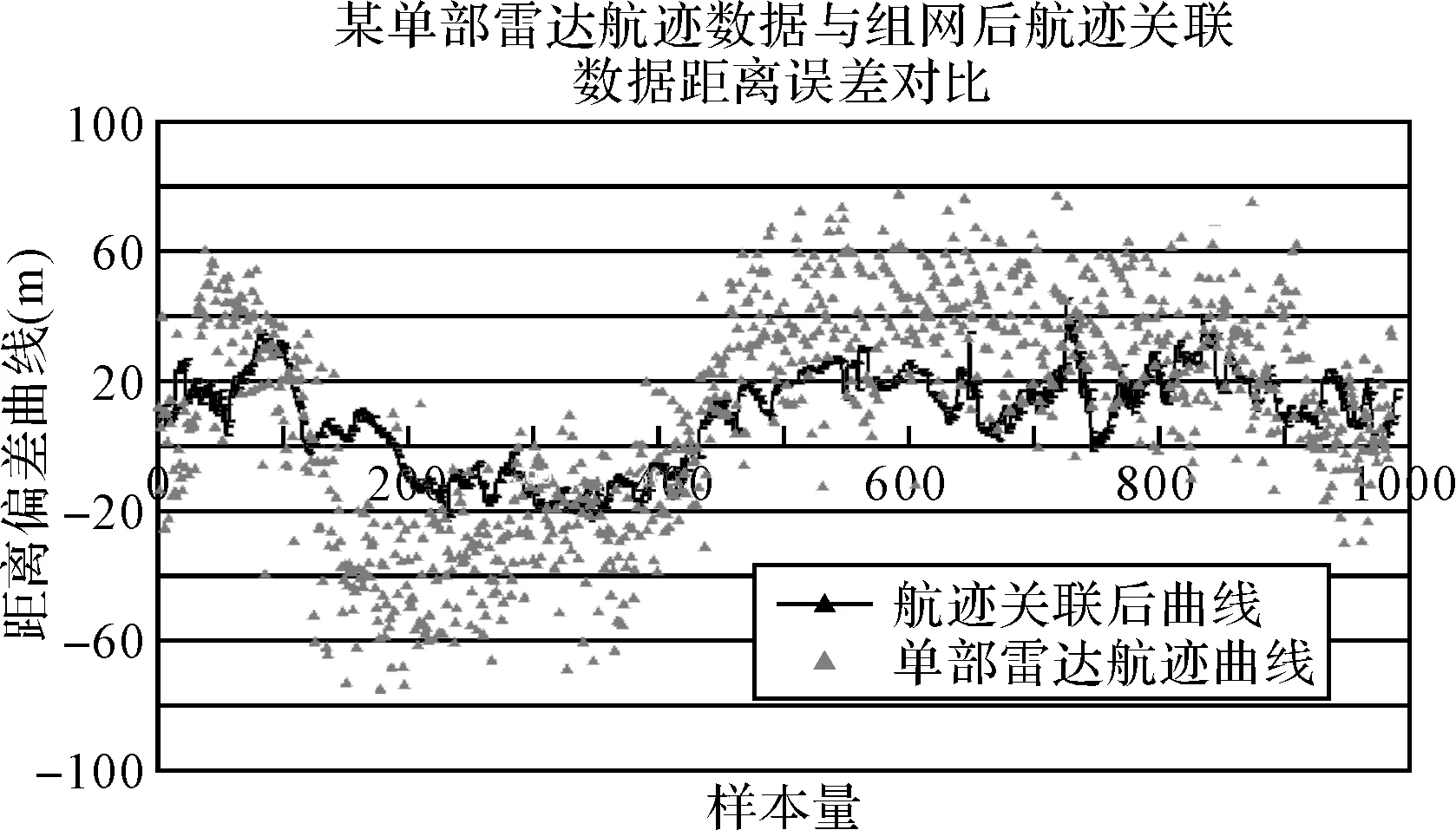
图2 目标航迹关联处理流程图

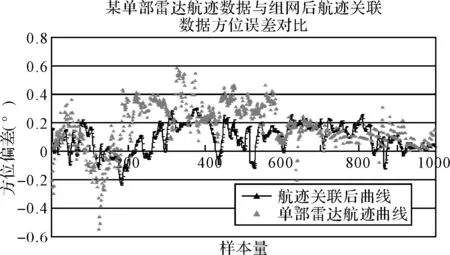
图3 目标航迹关联处理流程图

利用OriginPro软件作为平台，得到航迹关联数据与GPS数据对比曲线如图4所示。图中，粗直线表明单部雷达空域探测方位角范围为0°～33°和275°～360°，黑色粗线为GPS真值数据形成航迹，红色虚线为组网雷达数据航迹关联后航迹，可以看出，在密集的空情环境下，利用该系统进行雷达组网不但实现了全方位的空域探测以及目标的准确关联，而且无论是在目标直线段还是机动阶段，关联后航迹更加平滑，雷达网对机动目标的跟踪精度得到了提高。

图4 组网雷达航迹关联数据与GPS数据对比图

6 结语

本文针对作战系统实际需求，提出了对组网雷达航迹关联系统的实现方法,并对组网雷达系统数据偏差进行分析，对提出的航迹关联算法进行了验证,测试结果表明了算法的有效性与可行性，可应用于评估雷达组网在复杂电子战条件下的综合性能。

[1] 杨超，阚宗晖，徐莎莎，等.组网雷达模拟器数据融合中的航迹关联技术[J].火力与指挥控制，2012，37(11)：177-180. YANG Chao, KAN Zonghui, XU Shasha， et al. Research of Track Correlation Based on Data Fusion of Radar Simulator Network[J]. Fire Control & Command Contro，2012，37(11)：177-180.

[2] 罗琳玲，罗克露.基于最小二乘法的K-NN航迹关联算法研究[J].微计算机信息，2010，26(1)：176-178. LUO Linling, LUO Kelu. A K-Nearest Neighbor Track Correlation Algorithm Based on Least Mean Square [J].Microcomputer Information，2010，26(1)：176-178.

[3] 黄霄腾.多传感器航迹关联与融合算法研究[D].长沙：国防科学技术大学，2004. HUANG Xiaoteng. Study on Multisensor Track Association and Fusion Algorithm[D]. Changsha：National University of Defense Technology，2004.

[4] 石玥，王钺.雷达组网中联合数据关联与偏差估计方法研究[J].系统工程与电子技术，2006，18(11)：1668-1671. SHI Yue, WANG Yue. Research on joint data association and bias estimation method in radar networks[J].Systems Engineering and Electronics，2006，18(11)：1668-1671.

[5] 余安喜，胡卫东，郁文贤，等.航迹相关与融合的性能评估[J].系统工程与电子技术，2003,25(7)：897-900. YU Anxi， HU Weidong, YU Wenxian，et.al. Performance Evaluation for Track Correlation and Fusion[J].Systems Engineering and Electronics，2003，25(7)：897-900.

[6] 罗浩，尚朝轩，韩壮志，等.组网火控雷达自适应航迹关联算法研究[J].计算机测量与控制,2015，23(4)：1282-1284. LUO Hao, SHAN Chaoxuan, HAN Zhuang zhi, et al. Study on Adaptive Track Correlation Algorithm of Fire-Control Radar Network[J]. Comprter Measurement&Control,2015，23(4)：1282-1284.

[7] 方前学，杨建文.火控雷达组网航迹关联技术[J].火力与指挥控制,2013，12(38)：152-159. FANG Qianxue, YANG Jianwen. Track Association Technique in Fire Control Radar Network[J].Fire Control & Command Control,2013,12(38)：152-159.

[8] 陈昌质，阮怀林，户锋刚.分布式雷达网航迹关联的一种新方法[J].电子信息对抗技术,2008，12(23)：27-30. CHEN Changzhi, RUAN Huailin, HU Fenggang. A New Track Correlation Method in Distributed Radar Network[J].Electronic Information Warfare Technology,2008，12(23)：27-30.

[9] 盛安冬，戚国庆，王远钢，等.多种类雷达航迹辨识及融合的实用方法[J].火控雷达技术,2001，30(9)：15-18. SHENG Andong, QI Guoqing, WANG Yuangang，et al. A Method for Trajectory Identif ication and Fusion in Multitype Radars[J].Fire Control Radar Techology，2001，30(9)：15-18.

[10] 刘健波，王运锋.分布式雷达航迹融合关键技术研究[J].四川大学学报,2006，38(6)：119-122. LIU Jianbo, WANG Yunfeng. Study on the Algorithm of Distributed Radar Tracks Fusion[J]. Journal of Sichuan University,2006，38(6)：119-122.

[11] 李宏，许世军，刘诗斌，等.分布式雷达检测数据融合系统及性能分析[J].现代雷达,2005，27(4)：16-22. LI Hong, XU Shijun, LIU Shibin，et al. Distributed Radar Detection Data Fusion withMulti Radar andIts Performance Analysis[J].Modern Radar,2005，27(4)：16-22.

Analysis of Track Correlation Radar Net Based on Least Squares Method

CHEN Xin

(No. 91404 Troops of PLA, Qinhuangdao 066000)

Track correlation is a key technique in data fusion system of radar net, This paper presents an approximately complete set of track correlation distributed radar net system on least squares method for the practical requirement and the performance of the system is analyzed, the bias estimation can be eventually made by a recursive least square estimator.It efficiently enhances information using of the goal track.Also,the validity of the system is indicated by experimental results.

least squares method, radar net, track correlation

2016年5月17日,

2016年6月27日

陈欣，女，工程师，研究方向：雷达研究。

TP391

10.3969/j.issn.1672-9722.2016.11.013